Evaluation and comparison of diffusion MR methods for measuring apparent transcytolemmal water exchange rate constant

Abstract

Two diffusion-based approaches, CG (constant gradient) and FEXI (filtered exchange imaging) methods, have been previously proposed for measuring transcytolemmal water exchange rate constant k_in, but their accuracy and feasibility have not been comprehensively evaluated and compared. In this work, both computer simulations and cell experiments in vitro were performed to evaluate these two methods. Simulations were done with different cell diameters (5, 10, 20 µm), a broad range of k_in values (0.02 – 30 s⁻¹) and different SNR’s, and simulated k_in’s were directly compared with the ground truth values. Human leukemia K562 cells were cultured and treated with saponin to selectively change cell transmembrane permeability. The agreement between measured k_in’s of both methods was also evaluated. The results suggest that, without noise, the CG method provides reasonably accurate estimation of k_in especially when it is smaller than 10 s⁻¹, which is in the typical physiological range of many biological tissues. However, although the FEXI method overestimates k_in even with corrections for the effects of extracellular water fraction, it provides reasonable estimates with practical SNR’s and more importantly, the fitted apparent exchange rate AXR showed approximately linear dependence on the ground truth k_in. In conclusion, either CG or FEXI method provides a sensitive means to characterize the variations in transcytolemmal water exchange rate constant k_in, although the accuracy and specificity is usually compromised. The non-imaging CG method provides more accurate estimation of k_in, but limited to large volume-of-interest. Although the accuracy of FEXI is compromised with extracellular volume fraction, it is capable of spatially mapping k_in in practice.

Graphical abstract

Both diffusion-based CG (constant gradient) and FEXI (filtered exchange imaging) methods were evaluated and compared for measuring transcytolemmal water exchange rate constant k_in using computer simulations and cell experiments in vitro. Although compromised with accuracy and specificity, the FEXI method provides a sensitive way to measure k_in with more clinical potential.

INTRODUCTION

Transcytolemmal water exchange across cellular membranes plays an important role in a large variety of pathophysiological processes of living cells [1, 2]. It has been found that cell transmembrane permeability is correlated with cell membrane fluidity, which is an important indicator of living cell status [2]. In addition to these non-equilibrium water exchange, the equilibrium cell transmembrane permeability is also important and has been found to be increased significantly in tumors [3, 4] as well as neurodegenerative diseases such as Parkinson’s disease [5], and Alzheimer disease [6]. Therefore, the measurement of transmembrane permeability may provide insights for more specific assessments of the pathophysiological status of biological tissues.

In traditional biology, the cell transmembrane permeability or transcytolemmal water exchange is typically measured in cultured cells and the usage of such a method is limited in clinical practice [7]. By contrast, MRI provides a powerful and unique means capable of non-invasively mapping overall averaged transcytolemmal water exchange in vivo, although it is incapable of distinguishing permeabilities due to facilitated diffusion or osmosis. The current MRI methods measuring transcytolemmal water change can be summarized into two categories, i.e. relaxation- and diffusion-based methods. Both methods usually assume a two-component system (i.e. intra- and extra-cellular spaces) with water exchange at a single averaged rate constant (i.e. k_in, the transcytolemmal water exchange rate constant from intra- to extracellular space, whose relation to the cell transmembrane permeability P_m is given below in Eq.(1)). Relaxation-based methods usually use Gd-based contrast agents to selectively alter extracellular relaxation properties, and hence provide an opportunity to investigate the water exchange between intra- and extra-cellular spaces [3]. One disadvantage of this method is that it relies on the delivery of contrast agents to the extracellular space, which may be significantly limited in practice such as in brain regions with an intact blood-brain barrier (BBB). Moreover, multiple injections of Gd-based agents may increase the risk of nephrogenic systemic fibrosis in patients with concurrent acute or chronic kidney diseases [8].

By contrast, the diffusion-based methods do not require any exogenous probes and hence provide a more flexible and safer means to quantify transcytolemmal water exchange without such limitations. The behavior of two-component systems in diffusion measurements was thoroughly investigated by Karger et al. by assuming two freely-diffusing fractions [9], and later was improved to include restrictions on the intracellular water compartment [10–12]. Specifically, the CG (constant diffusion gradient) method has been developed to measure k_in by keeping diffusion gradients constant while varying diffusion times [13, 14]. However, the demand of very high b values (e.g. 580 ms/µm² in rat brain in vivo [13]) in the CG method constrains its practical applications, and hence it has been implemented only to measure the averaged k_in of a large volume-of-interest in a live rat brain in vivo in a non-imaging (spectroscopic) manner [13]. Recently, a filtered-exchange imaging (FEXI) method has been developed to measure apparent water exchange rate constants (AXR) [15–18]. Such a method employs a diffusion filter block and a diffusion detection block separated by a mixing time t_m. Although the obtainable apparent exchange rate AXR is actually k_in divided by the extracellular water fraction f_ex, the FEXI method provides a sensitivity to map k_in in humans in vivo [4, 16, 18, 19]. The FEXI method has been used to characterize meningioma and astrocytoma brain tumors [4, 18] and breast tumors [16], suggesting its clinical potential. However, despite its successful implementation, the FEXI method has not been fully validated before. Heating [15] and detergent [17] treatments have been performed to change cell membrane permeability in vitro in order to investigate the sensitivity of AXR to k_in, but these manipulations can also cause concurrent variations in other properties e.g. changes in intracellular diffusivity and cell size, which complicate data interpretation. Moreover, computer simulations, a powerful tool to investigate the direct relationship between microstructure and MR signals, have not yet been carried out to evaluate the accuracy of AXR obtained using the FEXI method.

In the current study, we use both computer simulations and well-controlled cell cultures in vitro with varying cell membrane permeabilities selectively to evaluate and compare the CG and FEXI methods. In computer simulations, the exchange rate constants obtained from both diffusion methods were compared directly with ground-truth values so that the accuracies of both methods could be assessed. In cell studies in vitro, saponin was used in fixed cells to selectively change overall cell membrane permeability without altering other cellular microstructures [20], which provides a means to precisely investigate how cell transmembrane permeability influences the measurements of k_in in both methods. Limitations and possible applications of both methods in practice are discussed.

MATERIALS AND METHODS

Theory

Both CG and FEXI methods assume a two-component system containing intra- and extracellular spaces. The transcytolemmal water exchange rate constant k_in is defined as the reciprocal of the averaged lifetime of intracellular water molecules τ_in, i.e. k_in = 1/ τ_in. k_in indicates the exchange rate constant from intra- to extracellular space. In a 3D system consisting of spherical cells, the cell transmembrane permeability P_m is related to k_in as [21, 22]

$$\frac{1}{P_m}=\frac{6}{d·k_{\mathit{\text{in}}}}-\frac{d}{10D_{\mathit{\text{in}}0}},$$ (1)

where d is the spherical cell diameter and D_in0 is the intrinsic intracellular diffusivity. D_in0 influences the measurements of P_m, as reported previously [23]. Note that, with the physiology relevant values of d, D_in, and k_in, the first term on the right side of Eq.(1) is typically much larger than the second term so that it usually dominates P_m.

CG (constant gradient) method

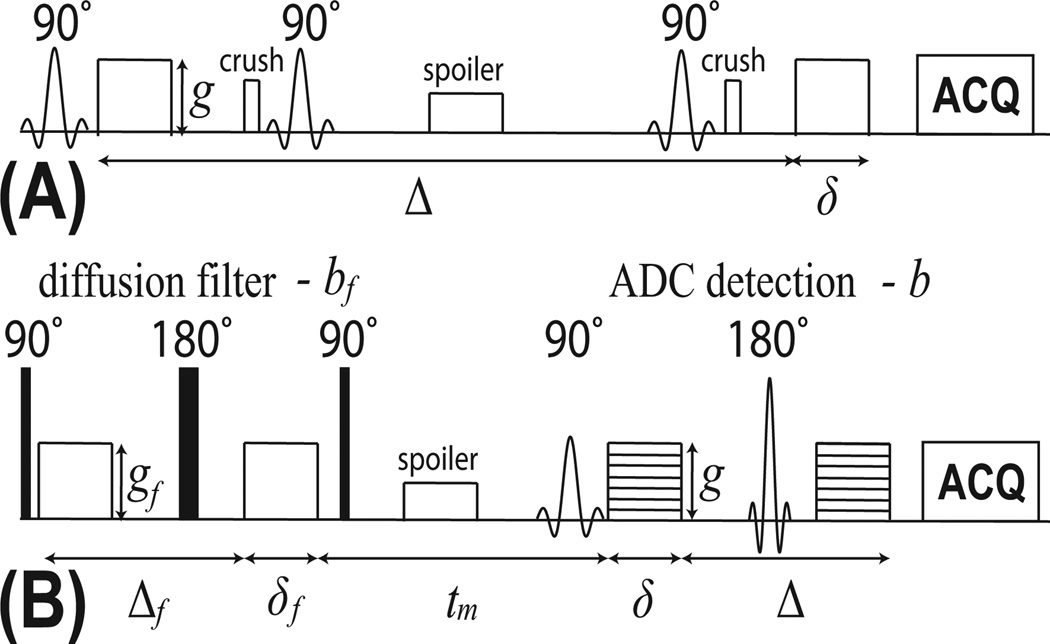
The pulse sequence of the CG method is shown in Figure 1A with g is the gradient strength, δ the gradient duration and Δ the gradient separation. With the short pulse approximation, the diffusion time t_D ≈ Δ. The diffusion MR signals arising from a two-component system with an average exchange rate constant can be expressed as

$$\{\begin{array}{c}\frac{\partial S_{\mathit{\text{in}}}}{\partial t}=-{\tilde{q}}^2{D}_{\mathit{\text{in}}}{S}_{\mathit{\text{in}}}-k_{\mathit{\text{in}}}{S}_{\mathit{\text{in}}}+k_{\mathit{\text{ex}}}{S}_{\mathit{\text{ex}}}\hfill \\ \frac{\partial S_{\mathit{\text{ex}}}}{\partial t}=-{\tilde{q}}^2{D}_{\mathit{\text{ex}}}{S}_{\mathit{\text{ex}}}-k_{\mathit{\text{ex}}}{S}_{\mathit{\text{ex}}}+k_{\mathit{\text{in}}}{S}_{\mathit{\text{in}}}\hfill \end{array},$$ (2)

where S_in and S_ex are signals arising from intra- and extracellular spaces, D_in and D_ex denote apparent intra- and extracellular diffusivities, k_ex = f_ink_in / f_ex is the transcytolemmal water exchange rate constant from the extra- to intracellular space, f_in and f_ex are the water fractions of the intra- and extracellular spaces, respectively, and q̃ = γδg, with γ being the gyromagnetic ratio. The solution to Eq.(2) based on Gaussian diffusion and a single diffusion encoding sequence is

$$S=S_{\mathit{\text{in}}}+S_{\mathit{\text{ex}}}=p_A\text{exp}(-{\tilde{q}}^2{D}_A{t}_D)+p_B\text{exp}(-{\tilde{q}}^2{D}_B{t}_D)$$ (3)

where D_A, D_B and p_A, p_B are referred to as apparent diffusion coefficients and apparent volume fractions, respectively, and their specific relation to real system parameters has been reported previously [11, 12]. In constant gradient (CG) measurements, if two conditions are satisfied [24], i.e. 1) a sufficiently long diffusion time is used, i.e. 4·t_D ·D_in / d² >> 1, and 2) the transcytolemmal water exchange rate constant is slow, i.e. q̃²D_ex >> k_in, k_in is given by [14]

$$k_{\mathit{\text{in}}}={-\frac{\partial \text{ln }S({\tilde{q}}^2,t_D)}{\partial t_D}|}_{{\tilde{q}}^2-\text{const}}={\tilde{q}}^2{D}_B$$ (4)

where D_B is the ADC when b = (γδg)² (Δ − δ / 3) is sufficiently high with a constant gradient g. Note that it has been reported that the applicability of the Karger Model also requires q̃²·l_c << 1, where l_c is the characteristic diffusion length on the order of cell size [24].

Figure 1.

Pulse sequence diagrams of (A) CG and (B) FEXI methods.

FEXI (filtered exchange imaging) method

Figure 1B demonstrates the sequence of the FEXI method, which consists of a “diffusion filter” followed by a diffusion detection block. The diffusion filter serves as a low-pass diffusion filter that changes the relative signal fractions of the intra- and extra-cellular spaces when they have different intrinsic diffusivities, and the diffusion detection block detects the relative signal contributions [4, 15–17]. The signals from the FEXI method are dependent on the mixing time t_m as

$$S(b,t_m)=S_0^{\prime }(t_m)\text{exp}[-b·\mathrm{A}\mathrm{D}\mathrm{C}\text{'}(t_m)],$$ (5)

where the t_m-dependent apparent diffusion coefficient ADC'(t_m) is related to the exchange rate as

$$\mathrm{A}\mathrm{D}\mathrm{C}\text{'}(t_m)=\mathrm{A}\mathrm{D}{\mathrm{C}}_0[1-\sigma ·\text{exp}(-t_m·\mathrm{A}\mathrm{X}\mathrm{R})].$$ (6)

where σ is the filter efficiency, and the apparent exchange rate AXR is actually k_in modulated by the extracellular volume fraction, namely, AXR

$$\mathrm{A}\mathrm{X}\mathrm{R}=k_{\mathit{\text{in}}}+k_{\mathit{\text{ex}}}=k_{\mathit{\text{in}}}/f_{\mathit{\text{ex}}}.$$ (7)

Note that the equilibrium condition f_in · k_in = f_ex · k_ex was used to derive Eq. (7). Therefore, unlike the direct measurement of k_in in the CG method, an apparent exchange rate AXR can be obtained from the FEXI method, which is proportional to k_in and more importantly AXR can be mapped in human subjects in vivo. Note that FEXSY (the spectroscopic version of FEXI) is capable of estimating the exchange rate constants by using large range of b values to separate intra- and extra-cellular contributions, and theoretically provide more accurate estimation of k_in not confounded by the extracellular fraction [15]. However, since the CG method has long been implemented in various applications by multiple groups, it is more suitable to represent the non-imaging diffusion methods to measure k_in. Therefore, FEXSY will not be discussed in the current work.

Cell sample preparation

Human myelogenous leukemia K562 cells were purchased from American Type Culture Collection (Manassas, Virginia, USA) and prepared as described previously [20]. Briefly, cells were cultured in Dulbecco’s modified eagle medium (DMEM) supplemented with 10% fetal bovine serum, 50 U/mL penicillin, and 50 µg/mL streptomycin (Invitrogen, Carlsbad, California, USA) under standard culture conditions in a humidified incubator maintained at 5% CO₂ and 37°C. Once enough cells were cultured, they were fixed and divided into three groups, each treated with vehicle (control) and low (0.025% w/v) and high (0.05% w/v) concentrations of saponin (Sigma-Aldrich, St. Louis, Missouri, United States). The cells were fixed by 4% paraformaldehyde for 2 hours and with saponin solution for 30 mins. Saponin is a type natural detergent that selectively removes membrane cholesterols and increases cell membrane permeability without altering other cell properties [25, 26]. Cells were centrifuged at g = 6000 for 2 mins. There were six pellets in each group, and each pellet contained approximately 30 million cells in a 0.65-mL Eppendorf tube. Note that fixation removes cell vitality which affects the transcytolemmal water exchange. However, the usage of saponin provides a means to increase passive diffusion so that overall averaged transcytolemmal water exchange rate constant can vary such as in physiologically relevant range with appropriate preparation.

MR experiments

All diffusion measurements were performed on an Agilent/Varian 4.7T MRI system with a 38-mm Doty coil for both transmission and reception. The magnet bore temperature was maintained at ~ 17°C using a cooling water circulation system. The non-imaging constant gradient NMR experiments were performed with a stimulated echo (STEAM) diffusion sequence as shown in Figure 1A. A 3-mm axial slice covering the central cell pellets was excited for the collection of NMR signals. The diffusion gradient duration δ = 10 ms, and the gradient separation Δ was varied in 30 increments. The maximum Δ was 832, 368, and 136 ms for cell samples with saponin concentrations of 0, 0.025%, and 0.05%, respectively. Diffusion gradients were applied on three axes simultaneously with amplitude g = 50 mT/m on each axis. To compensate for T₁ relaxation effects during the mixing time, the experiment was repeated with a lower gradient amplitude g = 5 mT/m to normalize the higher gradient datasets as described in [13, 20]. Other parameters included: repetition time (TR) = 3.5 sec; echo time (TE) = 25 ms; number of excitations (NEX) = 2; receiver bandwidth = 50 kHz and spectral resolution = 390.625 Hz. The total scan time for each constant gradient experiment was ~ 6 min.

The FEXI experiments were conducted with a diffusion-filtered spin-echo echo-planar imaging (SE-EPI) diffusion sequence as shown in Figure 1B. Diffusion gradients were applied on three axes simultaneously with duration δ = 6 ms in both the filter and detection blocks. The gradient separation Δ_f = 40 ms in the filter block and Δ = 20 ms in the detection block. The diffusion weighting b_f = 3000 s/mm² in the filter block and b = 0 and 1500 s/mm² in the detection block. Apparent diffusion coefficients (ADCs) were measured for 19 mixing times t_m: 7, 16, 26, 36, 46, 56, 66, 76, 86, 96, 106, 126, 146, 166, 186, 206, 256, 1006, 3006 ms. The equilibrium ADC was acquired with the filter inactive (b_f = 0 s/mm²) and t_m = 7 ms. Other parameters included: TR = 3.5 sec; TE = 38 ms; field of view = 25 × 25 mm; matrix size = 32 × 32; slice thickness = 3 mm and NEX = 8. The scan time for each mixing time t_m was ~ 3 min, yielding a total scan time of 60 min for each FEXI experiment. Note that there were altogether 30 signal data points acquired in the CG measurements and 20 signal data points acquired in the FEXI measurements.

Computer simulations

An improved finite difference method [27] was used in the simulations which incorporates the cell transmembrane permeability as described in [28]. The computer simulations were performed on modeled tissues as a collection of densely packed spherical cells positioned on a three-dimensional face-centered cubic structure (FCC) [29]. Water molecules were allowed to diffuse in intra- and extracellular spaces with a cell membrane of finite permeability separating the compartments. The simulation assumed D_ex = 2 µm²/ms, which is the diffusion coefficient of free water at 20°C [30], and D_in = 1 µm²/ms, a half of the free water diffusion coefficient [31]. We anticipate D_ex was close to the intrinsic diffusion coefficient of cell medium used in the experiments, while D_in may have minor effects on simulated results because the diffusion times used were relatively long. Three different cell diameters 5, 10, and 20 µm were simulated while the intracellular volume fraction was fixed as 61.8%. 18 ground truth k_in values were simulated in both CG and FEXI simulations: 0.02, 0.05, 0.1, 0.15, 0.3, 0.5, 0.75, 1, 1.5, 2, 2.5, 3, 5, 10, 15, 20, 25, 30 s⁻¹, corresponding to a very broad range of intracellular water lifetime τ_in from 33 ms to 50 sec. Note that intracellular water lifetime τ_in has been reported as 622±29 ms [13] or ~ 550 ms [32] in normal brain tissues and ~ 1.67 sec in mouse xenografts in vivo [3]. Therefore, the simulated range of intracellular water lifetimes covered the physiological relevant values. 19 mixing times were used in the FEXI simulations: 7, 20, 30, 50, 100, 150, 200, 300, 400, 500, 600, 800, 1000, 1500, 2000, 2500, and 3000 ms. All other parameters were the same as those used in the CG and FEXI measurements. For simplicity, the influences of relaxation were ignored in the simulations. Note that our simulations were based on a simplified tissue model that assumes cells are regularly packed, but recent findings have suggested this may lead a biased estimation of diffusion signals compared with more realistic random packing [33]. The total simulation time was ~14.5 hours for all of the CG simulations and ~14 hours for all the FEXI simulations.

To investigate the influence of signal-to-noise ratio (SNR) on the measurements of k_in using both diffusion methods, random noise was added to simulated signals according to the approach described previously [34]. A wide range of SNR from 20 to ∞, and 500 trials at each SNR level were simulated for each method.

Data analysis

All data analyses were performed using Matlab (Mathworks, Natick, MA, USA). For the CG experiments, the ADC of the slowly decaying component (i.e., D_B) was determined by linear regression using the last 10 data points. Note that the logarithms of MR signals corresponding to those data points are linearly dependent on b when b values are very high, and hence the number of data points chosen in data analyses has minor influence on the results (see Figure 2A). The intracellular exchange lifetime τ_in and transcytolemmal water exchange rate constant k_in were then derived from Eq. (4). For the FEXI experiments, a region of interest (ROI) was manually drawn on the central image, and ADC' values at each mixing time were calculated by fitting the ROI mean signals to exponential functions of the b value (S = S₀ exp(−b·ADC')). The ADC' measured with an inactive filter (b_f = 0 s/mm²) was regarded as that at infinite mixing time. AXR was determined by fitting ADC' as a function of t_m according to Eq. (6). Typical SNR was over 1000 for the CG measurements and > 200 for the FEXI measurements.

Figure 2.

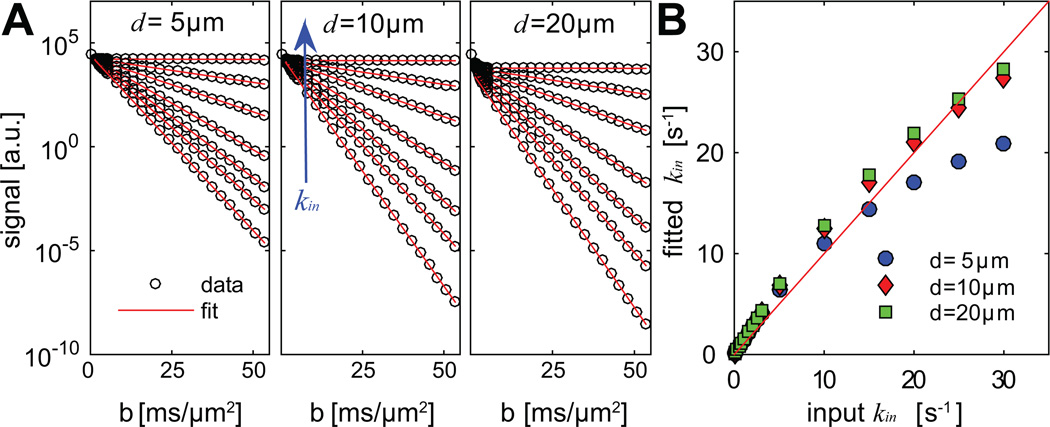
Computer simulated non-normalized signals from CG-experiments arising from three different cell diameters (A) and a comparison of the corresponding fitted vs ground truth k_in (B). Signals corresponding to seven k_in values are shown in (A): 0.02, 2, 5, 10, 15, 20, and 30 s⁻¹. Note that solid lines in (A) are used to better distinguish signals from different k_in values.

RESULTS

Simulated dependency on k_in and cell size

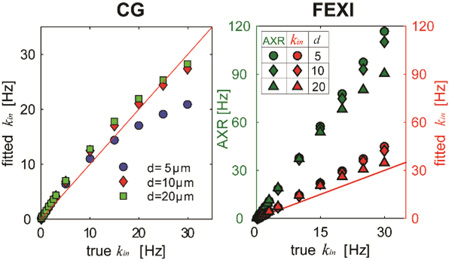
The simulated results using the CG method are shown in Figure 2. The logarithms of all diffusion-weighted signals show a linear dependence when b values are sufficiently high. The values of transcytolemmal water exchange rate constant k_in were calculated based on D_B and compared with the ground truth k_in shown in Figure 2B. The influences of cell diameter are minor for d = 5, 10, and 20 µm when k_in < 10 s⁻¹. Meanwhile, the fitted k_in values match well with the ground truth values in this k_in range (r = 1 and p < 0.01 for all three d values provided by the Spearman correlation). Figure 2B shows a non-linearity between fitted and ground truth k_in values. When k_in > 15 s⁻¹, there are large discrepancies between fitted and ground-truth k_in, especially for the smallest d (5 µm). For example, the fitted k_in is 30.6% lower when the ground-truth k_in is 30 s⁻¹, while the fitted k_in is 8.9% and 5.9% lower for d = 10 and 20 µm. These underestimates occurred at higher k_in values and may be due to the violation of the requirement of the CG method that the transcytolemmal water exchange should be slow enough [12]. Moreover, the CG method relies on the Gaussian phase approximation which may be invalid with high b values and small restriction sizes (e.g., cell size = 5 µm shown in Figure 2). Nevertheless, in the range of k_in < 10 s⁻¹, the CG method provides reasonable estimations of k_in with minor influences from cell diameter. Note that k_in < 10 s⁻¹ is physiologically relevant in biological tissues i.e. intracellular water lifetime τ_in > 100 ms [32]. The non-linearity in Figure 2B suggests that the accuracy of the CG method in estimating k_in is dependent on k_in itself and cell size. It should be noted that, in the highly permeable regime k_in > 15 s⁻¹ such as in apoptotic regions, the biased estimation of k_in limits the ability of the CG method to reliably characterize transcytolemmal water exchange.

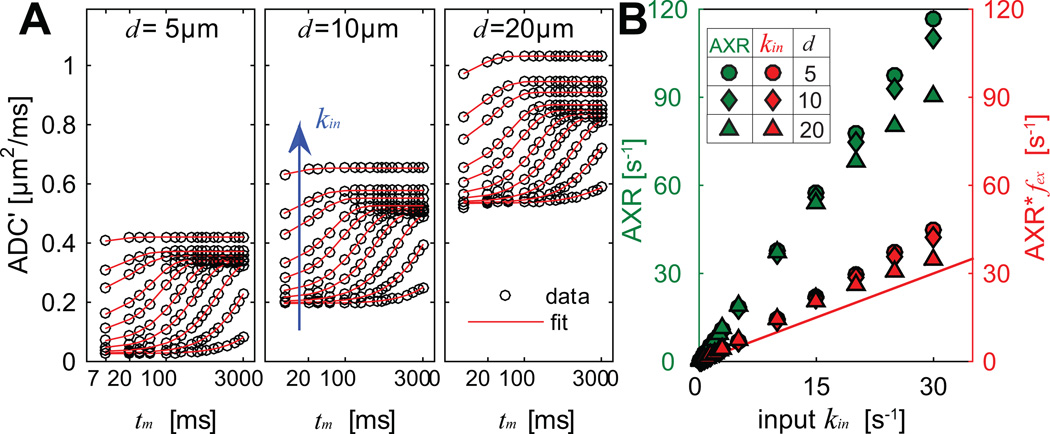
The simulated results using the FEXI method are shown in Figure 3. As expected, ADC' increases with t_m, k_in, and cell diameter d. All data are well described by Eq. (6). Comparisons of fitted AXR and k_in = AXR × f_ex vs ground truth k_in are provided in Figure 3B. The Spearman correlation provided r > 0.99 and p < 0.01 for any fitted AXR or k_in with ground truth k_in. The influences of cell sizes are minor when k_in < 15 s⁻¹, similar to the results using the CG method shown in Figure 2B. The discrepancies between fitted and true k_in are significantly larger than those of the CG method: the fitted k_in is 40% larger when true k_in > 5 s⁻¹, and 10% discrepancies occur only when true k_in < 0.1 s⁻¹ (τ_in > 10 sec, much longer than typical τ_in e.g. in normal brain [32]). This suggests the fitted k_in is overestimated using the FEXI method even with the correction for the effects of f_ex. However, both AXR and fitted k_in show approximately linear dependences on k_in, indicating AXR still provides a promising means to assess k_in non-invasively.

Figure 3.

Computer simulated ADC’ from FEXI experiments of three different cell diameters (A) and the comparison of AXR, fitted k_in vs ground truth k_in (B). ADC’ corresponding to ten k_in values were shown in (A): 0.02, 0.1, 0.3, 0.75, 1.5, 3, 5, 10, 15, and 30 s⁻¹. The x-axis is on logarithmic scale in (A), and solid lines in (A) are used to better distinguish signals from different k_in values.

Simulated influence of SNR

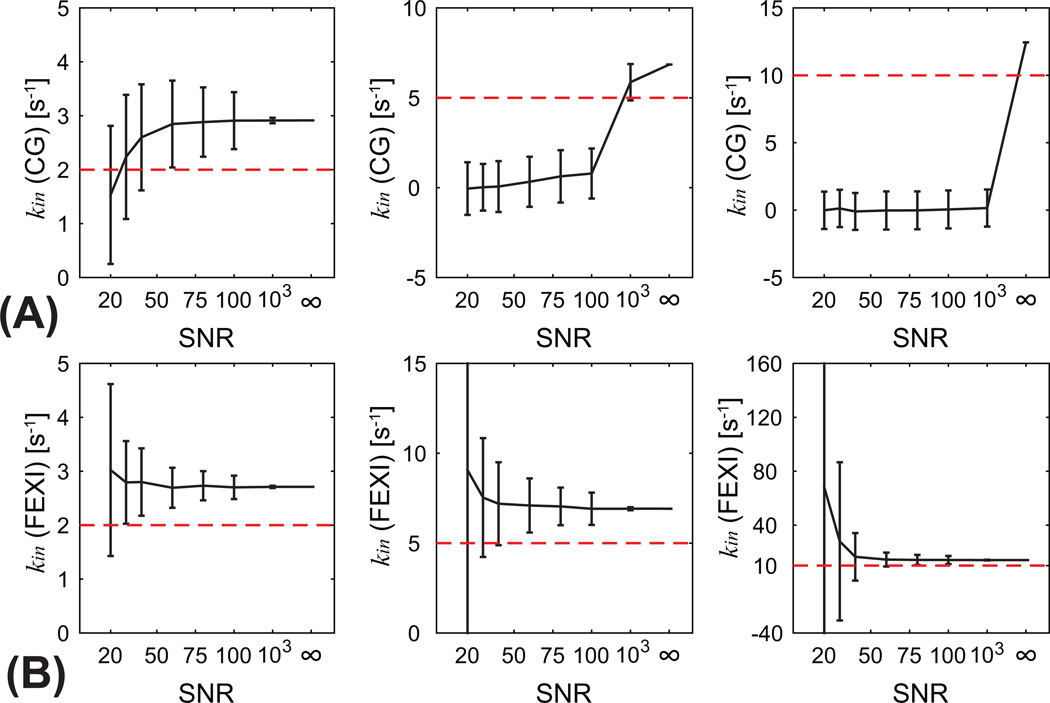
Figure 4 shows the simulated influence of SNR on the measurements of k_in using CG and FEXI methods for a typical cancer cell size d = 10 µm and three ground truth k_in values: 2, 5, and 10 s⁻¹. Under such circumstances, both CG and FEXI methods overestimate k_in even when SNR = ∞, although the CG method provide slightly more accurate result especially for ground truth k_in = 5, or 10 s⁻¹. For example, when ground truth k_in = 5 s⁻¹, the CG method estimates k_in of 6.85 s⁻¹, < 1% more accurate than k_in of 6.91 s⁻¹ estimated using the FEXI method. However, the noise influence on both methods is remarkably different. For ground truth k_in = 5 or 10 s⁻¹, the CG method estimated k_in all close to zeros when SNR is smaller than 100. This is because diffusion-weighted signals are under noise floor with very high b values, so that the CG method fails to estimate k_in. For example, Figure 4 shows normalized signals at high b values are very small, i.e., < 1e⁻⁴, so that even SNR = 100 is not sufficient to estimate k_in reliably. Under such circumstances, the linear fitting is dominated by noise and even negative k_in values might be obtained. However, reasonable k_in values can be obtained from the fittings when ground truth k_in = 2 s⁻¹, although deviated by ~ 1 s⁻¹. This is because when transcytolemmal water exchange rate constant is slow (e.g. τ_in = 500 ms), the signals were mainly dominated by intracellular restricted diffusion which decays much slower with respective to b values. By contrast, k_in (= AXR*f_ex) obtained using the FEXI method can estimate k_in reliably for all ground truth k_in values when SNR is sufficiently high (e.g. > 75). This suggests that the FEXI method is more robust at low SNRs which makes it possible for practical imaging, while the CG method typically requires very high SNR which makes it only suitable for large volume-of-interest in a non-imaging manner.

Figure 4.

The simulated influence of SNR on CG (A) and FEXI (B) methods for cell size d = 10 µm and three ground truth k_in values: 2 (left column), 5 (middle), and 10 (right) s⁻¹. Red dashed lines present ground truth values.

MR measurements of k_in

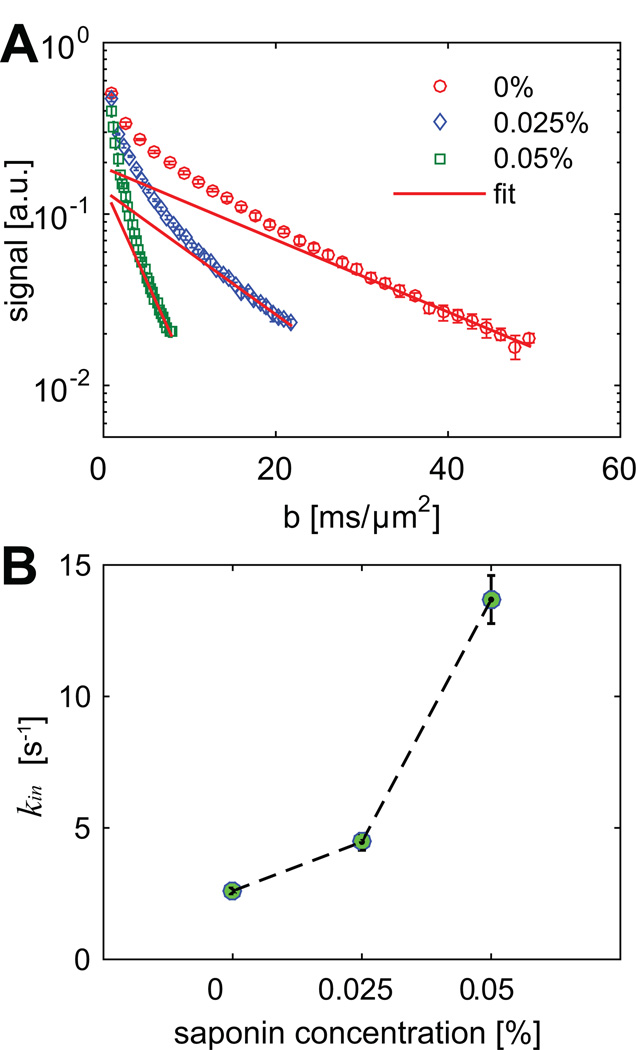
Figure 5 shows the measured signals and fitted k_in obtained in the CG measurements with three different saponin concentrations: 0, 0.025, and 0.05%. Note that most error bars are smaller than symbol sizes in Figure 5. As shown in Figure 5B, measured k_in increases significantly with higher concentration of saponin (r = 0.94 and p < 0.01). Recall that the ten signal data points with highest b values corresponding to each saponin concentration are used to fit k_in, which increases with higher concentrations of saponin when cell membranes are more permeable. Note that SNR in the CG measurements are over several thousands, and hence the influence of noise is negligible so that relatively higher k_in can be fitted, which is different from the results shown in Fig.4 with SNR < 100.

Figure 5.

The measured diffusion signals (A) and fitted k_in values (B) from CG experiments vs three different saponin concentrations. The error bars in both sub-figures represent standard deviations across all cell samples.

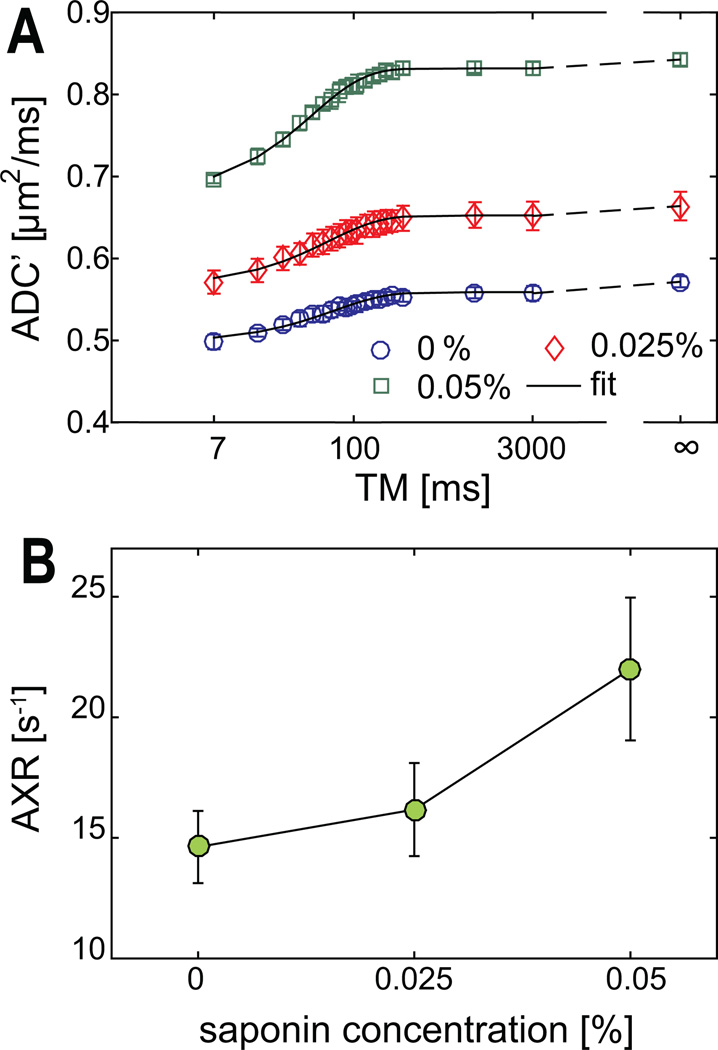
Figure 6 shows the measured ADC' and AXR values obtained from FEXI experiments of the same cell samples shown in Figure 5. All ADC' values are well described by the fits of Eq. (6). The fitted AXR’s increase significantly (r = 0.83 and p < 0.01) with higher concentrations of saponin as expected. Note that for the current experiments, only transmembrane permeability is expected to change with saponin concentration, indicating the cell membrane permeability changes have been detected by AXR. Note that the measured ADC at equilibrium (i.e., ADC' at infinite t_m) increases with higher concentrations of saponin, presumably due to the increased cross-membrane permeability. This is consistent with our previous study that the variations of cross-membrane permeability alone can cause significant ADC changes [20].

Figure 6.

The measured ADC’ (A) and AXR values (B) from FEXI experiments vs three different saponin concentrations. The error bars in both sub-figures represent standard deviations across all cell samples. The x-axis is on logarithmic scale in A.

Experimental correlation between results from CG and FEXI methods

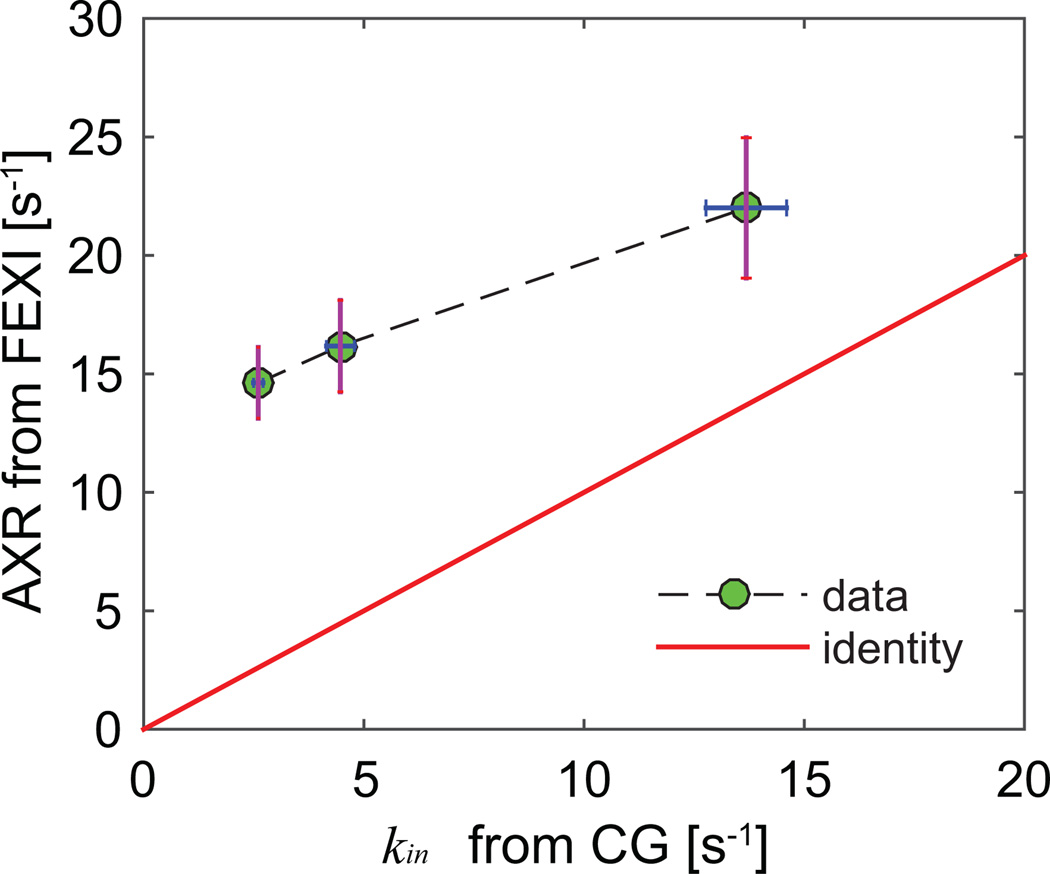
Figure 7 shows the correlation between AXR measured from the FEXI measurements vs k_in from the CG experiments. AXR from the FEXI measurements are significantly higher than k_in obtained using the CG methods due to the influence of extracellular water fraction f_ex. Compared with the simulated correlations shown in Figure 4, the discrepancies between AXR and k_in from the CG method are much larger, presumably due to the larger f_ex values in vitro compared with those used in the simulations. Nevertheless, AXR and k_in from the CG method are correlated in an approximately linear manner (r = 0.75 and p < 0.01), which implies the FEXI method may provide similar information as the CG method to probe the variations of transcytolemmal water exchange.

Figure 7.

The correlation between AXR measured from FEXI vs k_in from CG experiments. Each point represents the mean value from all cell samples treated with the same saponin concentration, and the error bars represent corresponding standard deviations.

DISCUSSION

The transcytolemmal water exchange rate constant k_in is not only an important indicator of the status of living cells, but also has a major influence on many MR measurements other than diffusion-weighted MR. For examples, it has been reported that k_in needs to be incorporated in DCE-MRI models for more accurate estimations of parameters when k_in is not fast enough [35]. Recent studies have also found relatively fast k_in values are essential for the validity of widely-used two-pool models to describe quantitative magnetization transfer (qMT) [36] and chemical exchange saturation transfer (CEST) [37] measurements. Therefore, a good estimate of k_in may not only provide a way to better characterize biological tissues, but also provides insights to better design experiments and data interpretation approaches for other MR methods.

Saponin used in our experiments has a concentration range of 71.4 to 223.2nM (based on the manufacturer provided data of 8–25% effective Sapogenin in their reagent), corresponding to 489 to 1527 saponin molecules per cell if they all interact with cell membranes. If saponin simply reaches equilibrium based on cell volume, there are 15 to 46 Saponin molecules per cell. This is certainly underestimated because there is a tendency for saponin to get into membranes due to the hydrophobicity nature. Hence, the actual number is estimated between 15 to 1527 saponin molecules per cell. By comparison, each mammalian cell has about 5×10¹⁰ lipids, and approximately a half is cholesterol. Therefore, the ratio of the number of saponin molecules to cell membrane cholesterol/lipid is extremely low. It is conceivable that, except increasing membrane permeability by removing a small number of cholesterols, the effect of saponin on other cell membrane structure is negligible at such a low concentration. This is consistent with previous studies that used detergents to change membrane permeability of fixed cells [26]. Note that Ref. [26] did not specifically measured cross-membrane water permeability, but found the enhanced permeability to large molecules such as oligonucleotides. Because water molecules are much smaller than oligonucleotides, we can reasonably infer that passive water permeability across fixed cell membrane increases after saponin treatment. This is consistent with our observation in this work.

The current work focuses on computer simulations and in vitro cell studies to generate varying transmembrane permeabilities that are within the physiologically relevant range. It should be noted that it is extremely challenging to fully mimic the cell environment in vivo. The fixation used in the current work removes vitality of cells which affects the membrane permeability significantly. However, an advantage of the current approach is that, with well-controlled conditions such as low concentrations of detergents, only membrane permeability is expected to be altered with minimal other side effects on fixed membrane structure. This is an advantage over the method of treating living cells using detergents, which may cause concurrent other effects that may confound the measurements and decrease the specificity to membrane permeability. Note that it may be more difficult for saponin to remove cholesterols on the surfaces of fixed cells because the membrane fluidity is expected to be greatly hindered after fixation. Nevertheless, our results suggest that the usage of saponin does increase the passive cross-membranes diffusion so that the overall averaged apparent transcytolemmal water exchange rate constant varies in a broad physiologically relevant range. Note that diffusion MR methods do not have the sensitivity to differentiate different types of water transport but characterize an overall averaged transcytolemmal water exchange rate constant. Therefore, even if our experimental settings cannot fully duplicate the in vivo environment, especially the inability to mimic active transport, our simplified tissue model system provides a testing framework to evaluate and compare both diffusion MR methods to characterize changes in membrane permeability.

The movement of molecules across a cell membrane can be either active or passive. The random diffusion is one main type of passive transport of water molecules, and there are other main types of water transport such as osmosis (caused by a cross-membrane osmotic gradient) and facilitated diffusion (transported by other molecules) [1]. It is important to emphasize that both diffusion MR methods used in the present work characterize an averaged cross-membrane permeability with an assumption of equilibrium water exchange. It is very challenging for the diffusion MRI methods to characterize the osmotic cross-membrane permeability with a dynamic net water transport. However, the dynamic net water transport may occur relatively slowly in some diseases. For example, it has been reported that it takes about 24 hours for extracellular space decreases from 20% to 4 – 10% after stroke [38, 39], much longer than typical scan time such as 45 mins for FEXI in vivo [4]. Under such circumstances, the apparent transcytolemmal water exchange rate constant is mainly dominated by diffusion or facilitated diffusion process under an assumption of close-to-equilibrium, which can be characterized using diffusion MR methods.

The CG (constant gradient) method has been developed for decades to measure an averaged transcytolemmal water exchange rate constant k_in [11, 12, 14]. However, such a method has not been comprehensively validated for 3D structures. A previous in vitro study used the water channel blocker pCMBS to decrease cell membrane permeability P_m [14], but an increase of P_m is more physiologically relevant in various diseases in practice [3, 5, 6, 20]. In addition, the use of pCMBS on living cells may cause other concurrent microstructural and physiological variations. The present study used saponin on fixed cells in vitro to selectively increase P_m without causing other microstructural variations [20]. There was one previous computer simulation study of the CG method performed on 2D cylindrical tissues with τ_in from 231 to ∞ ms [12], without considering faster transcytolemmal water exchange (τ_in < 100 ms) which occurs in many diseases [3, 4]. A large range of τ_in from 33 ms to 50 sec was simulated in the current study to investigate the accuracy of the CG method to measure k_in. The results suggest that the CG method provides a reasonable estimation of k_in especially when k_in < 10 s⁻¹, corresponding to τ_in > 100 ms which is in the physiological range of normal tissues. For k_in > 10 s⁻¹, the k_in obtained using the CG method still increases monotonically with ground truth k_in, suggesting the CG method provides useful information on k_in even with fast transcytolemmal water exchange which violates the requirements of the CG method. Because very high b values are necessary in the CG method which results in SNRs that are too low for high spatial resolution imaging, the CG method is preferred to detect k_in of a large volume-of-interest spectroscopically when spatial mapping is not required.

Other than by heating [15] and detergent [17] treatment studies, the FEXI method has not been fully validated up to date. The dependence of AXR on both k_in and f_ex makes it difficult to interpret FEXI data. The computer simulations used in the current study provide an opportunity to investigate the precise relation between true and fitted k_in values using the FEXI method. Compared with the CG method, our simulations suggest that the FEXI method provides slightly less accurate results about transcytolemmal water exchange even after correction for the effects of f_ex at very high SNRs. Our simulations show that FEXI overestimates k_in, which may be because the simulations and experiments violate some assumptions used in deriving Eq. (6) [4, 15, 17]. For example, the b = 1500 s/mm² used in the diffusion detection block yields non-mono-exponential behavior for smaller cell sizes (5 µm), which violates the small b assumption to derive Eq. (6). Our simulations suggest this can lead to an overestimation k_in. Moreover, the influences of non-uniform relaxation were not considered in the simulations, which may further increase the discrepancies between fitted and true k_in. Despite these disadvantages, the FEXI method does not require extremely high SNR’s as the CG method. The fitted AXR and k_in values obtained in computer simulations showed approximately linear dependence on ground truth k_in (see Figure 3), indicating they still provide a reasonable means to measure k_in. In the cell measurements in vitro with sufficiently high SNR’s, fitted AXR values correlated well with k_in fitted using the CG method, suggesting they may provide similar information on variations of transcytolemmal water exchange rate constant. It should be pointed out that the increased cell membrane permeability P_m found in pathological tissues will cause larger errors in AXR, and the possibly variable f_ex will further complicate the interpretation of FEXI data in practice. As shown in Fig.2 and Fig.3, with higher k_in values (i.e., fast exchange), the fitted k_in deviates further from ground truth values in the simulations. This indicates the influences of the violation of slow exchange approximation in both methods. However, both methods provide reasonably well estimation of k_in when k_in < 10 s⁻¹, which is typical for biological tissues. It should be prudent to interpret data from highly permeable tissues such as apoptotic regions, in which k_in could be > 15 s⁻¹ [3]. Nevertheless, the FEXI method provides a flexible and non-invasive imaging method capable of spatially mapping k_in in humans [4, 16], which may have considerable clinical potential.

For the CG method, two conditions need to be satisfied [24], i.e. 1) a sufficiently long diffusion time is used, i.e. 4·t_D·D_in / d² >>1, and 2) the transcytolemmal water exchange rate constant is slow, i.e. q̃²D_ex >> k_in. Note that very high b values are required in CG measurements with a fixed gradient strength (as well as the q value) so that the diffusion times are usually very long to meet the first condition. Meanwhile, the fixed gradient duration is much shorter than long diffusion times, and hence we do not expect the gradient duration to affect the CG measurements significantly. As shown in Fig.2, the CG method shows different accuracy with different k_in values, i.e., more accurate with k_in < 10 s⁻¹ than those with k_in > 15 s⁻¹. This discrepancy is presumably due to how the slow exchange approximation is satisfied. Therefore, it is important to note that CG measurements may provide biased results when transcytolemmal water exchange rate constant is too large, such as in apoptotic regions.

For the FEXI method, the diffusion times used in either the filter or the detection PGSE blocks are chosen in such a way that significant transcytolemmal water exchange is expected to occur mainly during the mixing time and not much during each of the PGSE blocks. Ideally, the diffusion time t_D should be much smaller than mixing time t_m. Therefore, shorter diffusion times are preferred, which also limits the choices of gradient durations. Note that both diffusion times and gradient durations are fixed, and only mixing time t_m is allowed to vary in FEXI measurements. Therefore, we do not expect slightly different diffusion times and gradient durations in practical ranges would significantly affect the FEXI results. It is of interest to investigate the exact influence of different choices of diffusion times and gradient durations on FEXI measurements, but is out of the main scope of current work.

It is desirable to measure intra- or extracellular water fraction f_in or f_ex = 1 − f_in and use this information to correct AXR values obtained in FEXI measurements for a better estimation of k_in. DCE-MRI and diffusion-weighted MRI methods have been proposed to measure f_in non-invasively. However, recent studies have found the accuracy of the measurements of f_in are significantly affected by k_in themselves. A recent study [40] reports that f_in values obtained from either quantitative PGSE (pulsed gradient spin echo) [41] or OGSE (oscillating gradient spin echo) [42, 43] diffusion sequences are significantly underestimated due to transcytolemmal water exchange, while fitted cell size values are less influenced. Another study found out that “DCE-MRI is not a reliable biomarker of extracellular space for a range of physiological conditions” confirmed with histology analysis [44]. These findings demonstrate the difficulties of reliably estimating f_in or f_ex in vivo, making it even more challenging to directly measure k_in using the FEXI method.

Previous water exchange studies with red blood cells typically use Gd to “selectively” change extracellular relaxation properties [45]. The estimated k_in has been reported as 52.4 s⁻¹, much larger than the 2.6 s⁻¹ of untreated K562 cells in the current study. This is anticipated because the mean K562 cell diameter is ~19 µm [20], much larger than typical red blood cell size of 6 – 8 µm. Note that the Gd-based method is also model based and has its own limitations. It has been reported that Gd-based contrast agents may introduce magnetic susceptibility gradients which cross compartmental boundaries and alter R₂ measurements [32], which in turn effectively change relative water fractions. Even if R₁ measurements have been widely used to estimate water exchange rate constant [32, 46], the contamination of MT on R₁ measurements may significant alter the fitted water exchange rate constant, as shown by Prantner et al. [47]. Due to a lack of “gold standard” method to accurately quantify the transcytolemmal water exchange rate constant non-invasively, it is challenging to fully validate the accuracy of the relaxation- and diffusion-based methods to estimate k_in.

The current study focuses on the evaluation and comparison of diffusion MR methods for measuring transcytolemmal water exchange rate constant k_in using computer simulations and cultured cells in vitro with varying cell transmembrane permeabilties. Note that other biological tissues properties (such as relaxation and diffusion rates of intra- and extracellular space, cell shape, and diffusion anisotropy [19]) and acquisition strategies (such as choices of readout sequences) might influence the measurements of k_in as well. The comprehensive investigation of all these influences on k_in measurements is desirable in future studies.

CONCLUSIONS

Two diffusion-based methods, CG (constant gradient) and FEXI (filtered exchange imaging) methods, were comprehensively evaluated and compared using both computer simulations and well-controlled cultured cells with varying cell transmembrane permeabilties. The results suggest that, with sufficient SNR’s, the CG method provides reasonably accurate estimations of transcytolemmal water exchange rate constant k_in when it is smaller than 10 s⁻¹, which is in the physiological range of many biological tissues. However, the CG method requires high SNR which makes it applicable only with large volumes-of-interest. Although the FEXI method constantly overestimates k_in even with corrections for the effects of extracellular water fraction, it provides reliable estimates with practical SNR’s and more importantly, results from the FEXI method agrees well with those from the CG method with high SNR’s experimentally. Considering the feasibility of spatially mapping k_in in humans in vivo, the FEXI method is of clinical potential as shown recently although its absolute accuracy is compromised.

Highlights.

• Both CG or FEXI methods are sensitive to transcytolemmal water exchange rate constant k_in

• The CG method provide accurate estimation of k_in with high SNR and k_in < 10 s⁻¹

• The FEXI method overestimates k_in but agrees with the CG method experimentally

• The FEXI method might have greater clinical potential compared with the CG method