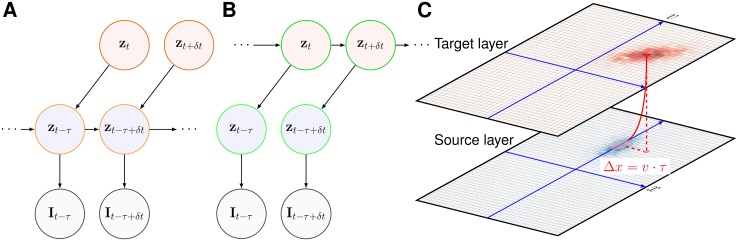
Fig 2. Diagonal Markov chain.

In the current study, the estimated state vector z = {x, y, u, v} is composed of the 2D position (x and y) and velocity (u and v) of a (moving) stimulus. (A) First, we extend a classical Markov chain using Nijhawan’s diagonal model in order to take into account the known neural delay τ: At time t, information is integrated until time t − τ, using a Markov chain and a model of state transitions p(z_t|z_t−δt) such that one can infer the state until the last accessible information p(z_t−τ|I_0:t−τ). This information can then be “pushed” forward in time by predicting its trajectory from t − τ to t. In particular p(z_t|I_0:t−τ) can be predicted by the same internal model by using the state transition at the time scale of the delay, that is, p(z_t|z_t−τ). This is virtually equivalent to a motion extrapolation model but without sensory measurements during the time window between t − τ and t. Note that both predictions in this model are based on the same model of state transitions. (B) One can write a second, equivalent “pull” mode for the diagonal model. Now, the current state is directly estimated based on a Markov chain on the sequence of delayed estimations. While being equivalent to the push-mode described above, such a direct computation allows to more easily combine information from areas with different delays. Such a model implements Nijhawan’s “diagonal model”, but now motion information is probabilistic and therefore, inferred motion may be modulated by the respective precisions of the sensory and internal representations. (C) Such a diagonal delay compensation can be demonstrated in a two-layered neural network including a source (input) and a target (predictive) layer [44]. The source layer receives the delayed sensory information and encodes both position and velocity topographically within the different retinotopic maps of each layer. For the sake of simplicity, we illustrate only one 2D map of the motions (x, v). The integration of coherent information can either be done in the source layer (push mode) or in the target layer (pull mode). Crucially, to implement a delay compensation in this motion-based prediction model, one may simply connect each source neuron to a predictive neuron corresponding to the corrected position of stimulus (x + v ⋅ τ, v) in the target layer. The precision of this anisotropic connectivity map can be tuned by the width of convergence from the source to the target populations. Using such a simple mapping, we have previously shown that the neuronal population activity can infer the current position along the trajectory despite the existence of neural delays [44].