Automated Tuning for Parameter Identification and Uncertainty Quantification in Multi-scale Coronary Simulations

Abstract

Atherosclerotic coronary artery disease, which can result in coronary artery stenosis, acute coronary artery occlusion, and eventually myocardial infarction, is a major cause of morbidity and mortality worldwide. Non-invasive characterization of coronary blood flow is important to improve understanding, prevention, and treatment of this disease. Computational simulations can now produce clinically relevant hemodynamic quantities using only non-invasive measurements, combining detailed three dimensional fluid mechanics with physiological models in a multiscale framework. These models, however, require specification of numerous input parameters and are typically tuned manually without accounting for uncertainty in the clinical data, hindering their application to large clinical studies. We propose an automatic, Bayesian, approach to parameter estimation based on adaptive Markov chain Monte Carlo sampling that assimilates non-invasive quantities commonly acquired in routine clinical care, quantifies the uncertainty in the estimated parameters and computes the confidence in local predicted hemodynamic indicators.

1. Introduction

Acquired cardiovascular disease, specifically atherosclerotic coronary artery disease, continues to be a major cause of morbidity and mortality worldwide. About one in seven deaths in the United States is caused by obstructive coronary artery disease, with an associated total annual cost of about $108.9 billion [1]. Hemodynamics are known to play an important role in the pathophysiology of atherosclerotic coronary artery disease [2]. However, current tools to non-invasively study coronary artery hemodynamics are primarily deterministic.

Computational simulations of coronary artery flow provide a means to calculate hemodynamics that can aid in risk stratification, treatment planning, and improve understanding of disease progression. These tools have potential for clinical impact and have been used in optimizing coronary stent design [3] thrombotic risk stratification for Kawasaki disease [4, 5], analyzing the correlation between wall shear stress and atherosclerosis [6], and non-invasive assessment of fractional flow reserve [7].

State-of-the-art cardiovascular simulation tools employ lumped parameter networks (LPN, formulated through a set of ODEs) in a multiscale framework to specify the boundary conditions at inlets and outlets of a 3D patient-specific model, using circuit element representations of the heart and distal circulation [4, 8]. The numerous LPN parameters (e.g. resistance, compliance, inductance, etc.) are typically tuned so the simulation results match a set of clinical data, such as the patient’s blood pressure, stroke volume, and ejection fraction. Using current tools, manual tuning of these parameters is required, but is time consuming, operator dependent, and does not account for clinical data uncertainty. To overcome this difficulty, various automatic approaches to parameter estimation have been discussed in the literature (see, e.g., [9, 10, 11, 12, 13, 14, 15]), in most cases providing only point estimates for the unknown parameters.

In this study, we follow a Bayesian perspective on estimation, treating unknown parameters as random variables and using an iterative approach with multiple chains to sample from their joint posterior distribution. A significant effort is also spent in detecting unimportant parameters, using local and global identifiability metrics to reduce the dimensionality of the estimation problem, resulting in a reduced set of identifiable parameters. By sub-sampling the parameter realizations obtained from DREAM (see Section 4.2) that result in reasonable matching among targets, we also compute an ensemble of multiscale model solutions and estimate the uncertainty of resulting output quantities of interest (wall shear stress and oscillatory stress index maps on the coronary arteries) using Monte Carlo simulation.

The main contributions of this paper are to present an automatic approach (combining parameter identifiability and Bayesian estimation) to determine optimal LPN parameters for coronary artery simulations from non-invasive clinical targets, and to quantify their variability due to both clinical data uncertainty and the presence of non-indentifiable parameter combinations. Moreover, we use a Monte Carlo approach to propagate LPN parameter uncertainties to full multiscale model results, e.g., time averaged wall shear stress (TAWSS) and oscillatory shear index (OSI). This is in contrast to previous deterministic approaches in which results are typically obtained for a single set of boundary conditions, with no possibility of quantifying confidence in local hemodynamic indicators.

2. Multiscale coronary simulations

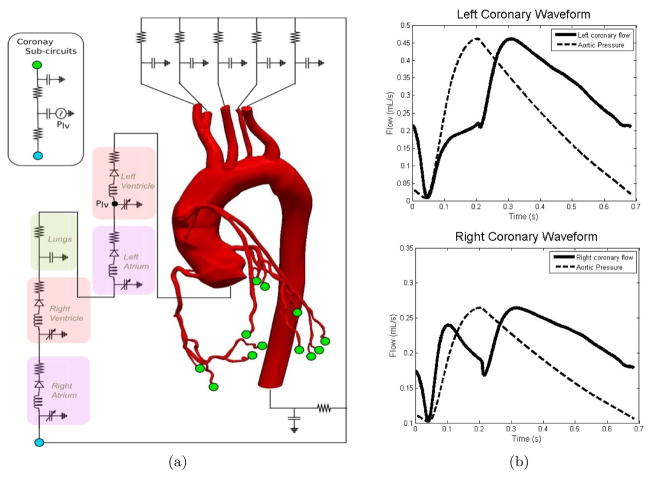
A multiscale model of the coronary circulation is shown in Figure 1 (a) and consists of coupling an LPN model with a 3D representation of the aorta and coronary arteries. Patient-specific models of the aorta and coronary arteries are constructed from CT images and combined with finite element flow simulations using the open source software package SimVascular [16]. The finite element mesh consists of tetrahedral elements, and a stabilized finite element technique using the generalized-α method is used to solve the time dependent Navier-Stokes equations [17, 18]. The solutions are then post-processed to obtain quantities of interest such as wall shear stress and oscillatory shear index.

Figure 1.

(a) Schematic view of a multiscale patient-specific model of the coronary circulation and (b) typical left (top) and right (bottom) coronary artery flow waveforms. A scaled down aortic pressure waveform is shown to highlight the out of phase nature of coronary flow.

The selected LPN layout is inspired by previous work [19] and includes compartments for each of the four chambers of the heart, the pulmonary arteries, modified Windkessel models for the systemic circulation, and sub-circuits for the coronary circulation which are coupled to the left ventricular pressure. It contains 35 parameters with components mimicking viscous resistance, vessel compliance, and blood inertia. Ventricular contraction is modeled using an elastance formulation [20], while an activation function formulation is used for the atria. The governing equations for the coronary LPN are outlined in [19], with a key difference in this study being that the relative coronary outlet resistances are scaled according to Murray’s Law [21]. We finally stress that the similarities between the proposed approach and [19] are only relative to the lumped parameter model layout used to simulate coronary flow. The parameter estimation approach is, however, fundamentally different. In [19] the authors used deterministic patient-specific parameters to quantify coronary hemodynamics, studying the effect of changes in graft path and angle of anastamosis. Here, we focus on an automated approach to estimate the uncertainty in the LPN parameters induced by clinical data variability. We then use Monte Carlo simulation to quantify the uncertainty in local hemodynamic results, allowing estimation of confidence in the 3D results. Instead of performing a multi-scale simulation for a single set of boundary conditions, we rather explore an ensemble of realizations of boundary conditions, all of which are compatible with the patient-specific data.

One of the goals of this multiscale framework is to model the out of phase behavior of coronary flow. As shown in Figure 1(b), the left coronary waveform is described by low flow in systole and high flow in diastole, while the right coronary waveform is characterized by nearly equal flow peaks in systole and diastole. This result is in agreement with clinical observation.

3. Clinical targets

The clinical targets considered in this study were acquired through routine measurements, population average values, echocardiography data, and literature data to supplement the non-invasive measurements on coronary flow. A list of the clinical targets, including a short description, associated uncertainties, and assigned weight factors (see Section 4.1) can be found in Table 1.

Table 1.

List of clinical targets considered in this study. Uncertainties are represented as standard deviations from the measured quantity for patient-specific targets, or standard deviations from the mean reported in literature.

Target	Description	Uncertainty	Weight	Specific/Literature
Min Pao	Diastolic aortic pressure	10% measured	1	Patient-specific
Max Pao	Systolic aortic pressure	10% measured	1	Patient-specific
Mean Pao	Mean aortic pressure	10% measured	1	Patient-specific
Aor − Cor flow split	Percentage of cardiac output to coronaries	10% mean	1	Literature
Stroke Volume	Blood volume ejected each heart contraction	10% measured	1	Patient-specific
Mean Ppulm	Mean pulmonary pressure	3.3 mmHg	2	Literature
Ejection Fraction	Percentage of LV blood volume ejected per contraction	10% measured	1	Patient-specific
Mitral E/A ratio	Ratio of early to late flows into the LV	20% measured	2	Patient-specific
Mitral valve open %	Percentage of cardiac cycle that mitral valve is open	15% measured	2	Patient-specific
Aortic valve open %	Percentage of cardiac cycle that aortic valve is open	15% measured	2	Patient-specific
Pulm valve open %	Percentage of cardiac cycle that pulmonary valve is open	15% measured	2	Patient-specific
Max Prv − Pra	Systolic pressure difference between the RV and RA	25% measured	2	Patient-specific
Mean Pra	Mean RA pressure	40% measured	1	Patient-specific
Lcor peak ratio	Left coronary peak flow ratio in diastole vs. systole	0.8	1	Literature
Lcor total ratio	Left coronary flow volume ratio in diastole vs. systole	2.53	1	Literature
Lcor 1/3 FF	Percentage of left coronary flow volume in first 1/3 of cardiac cycle	0.02	1	Literature
Lcor 1/2 FF	Percentage of left coronary flow volume in first 1/2 of cardiac cycle	0.03	1	Literature
Rcor peak ratio	Right coronary peak flow ratio in diastole vs. systole	0.3	1	Literature
Rcor total ratio	Right coronary flow volume ratio in diastole vs. systole	1.08	1	Literature
Rcor 1/3 FF	Percentage of right coronary flow volume in first 1/3 of cardiac cycle	0.07	1	Literature
Rcor 1/2 FF	Percentage of right coronary flow volume in first 1/2 of cardiac cycle	0.07	1	Literature

The aortic pressures are the patient’s cuff pressures taken at the time of the echocardiogram, which is a good approximation of the aortic pressure. The patient-specific data collected from echocardiography include: stroke volume [22], ejection fraction, ratio of early to late flows into the left ventricle, valve opening times relative to the heart cycle duration, systolic pressure difference between the right ventricle and right atrium measured from tricuspid valve regurgitation [23], and the mean right atrial pressure estimated from the diameter and degree of inspiratory collapse of the inferior vena cava [24] (refer to [25, 26, 27] for modern guidelines on performing and interpreting echocardiograms).

Literature data was included to improve identifiability of the model parameters. Specifically, we assumed a mean pulmonary pressure of 14.0 mmHg [28] and that 4% of the cardiac output is distributed to the coronaries [29]. We also used the Doppler flow wire measurements reported in [30] as a reference for the out of phase behavior of the left and right coronary waveforms. This includes diastolic to systolic peak flow ratio, the diastolic to systolic blood volume flowing through the coronary arteries, and the ratio of the flow occurring in the first 1/3 and 1/2 of the heart cycle.

Standard deviations for these targets were determined from the literature and personal communication with clinicians about their relative confidence in each measurement. Measurements of ejection fraction have relatively small uncertainty, since they depend only on tracking the left ventricular wall during echocardiography. The geometry of the left ventricular wall can clearly be seen throughout the cardiac cycle, thus these quantities are determined with good confidence. Other echocardiographic measurements depend on the reliability of echocardiography to measuring flow. Doppler flow measurements depend on the orientation of the measuring probe relative to the direction of flow, and some patients do not admit clear flow profiles. The targets depending on echocardiographic flow measurements (mitral valve E/A ratio, amount of time the valves are open, and max P_rv − P_ra) thus are assigned higher uncertainties. Finally, the heart rate is assumed deterministic (not subject to tuning), and is collected at the time of echocardiography.

4. Methods

4.1. Statistical model

Consider a set of d parameters, y = {y₁, …, y_d} statistically characterized by their joint probability distribution ρ (y) and denote y^k as a generic realization sampled from ρ (y). Also consider a set of m outputs o = {o₁, …, o_m}, one for each of the m clinical targets d = {d₁, …, d_m} with joint distribution ρ (d). We then consider the LPN model as a map G : ℝ^d → ℝ^m, that returns a vector of results o^k given a vector of input parameters y^k, or in other words, o^k = G(y^k). The error ε between the model outputs and our clinical targets is

$$\mathit{\epsilon }=\mathbf{d}-\mathbf{G}(\mathbf{y})$$ (1)

and accounts for both the uncertainty in the clinical measurements and approximations due to modeling a complex physiological behavior with a simplified LPN model. Since we do not have any knowledge about how these clinical measurements might be correlated, we assume a diagonal covariance for ε. With these assumptions, the likelihood function takes the form:

$$P(\mathbf{d}\mid \mathbf{y})=\frac{1}{\sqrt{{(2\pi )}^m{\displaystyle \prod _{i=1}^m}{\omega }_i{\sigma }_i^2}}\mathbf{exp}\left(-\frac{1}{2}\sum _{i=1}^m\frac{{[d_i-G_i(\mathbf{y})]}^2}{{\omega }_i{\sigma }_i^2}\right),$$ (2)

where d_i is the i-th clinical target with variance ${\sigma }_i^2$, G_i(y) is the corresponding model output, and ω_i is a weight factor. The weights are included to modulate our ability to match certain targets. For the purpose of tuning boundary conditions, we have chosen to place higher priority (i.e., ω_i = 1) on the targets that directly affect the 3D results, such as the aortic pressure and the various coronary flow targets, and lower priority (i.e., ω_i > 1) on the targets in the heart compartment, which have a smaller impact.

Once the likelihood for a given parameter realization has been determined, the posterior distribution of the model parameters conditioned on the clinical data can be formulated through Bayes’ Rule, P (y|d) ∝ P (d|y) P (y). In our study, we use uniform priors defined through admissible parameter ranges. The adoption of more informative priors would, in general, be beneficial and likely result in reduced parameter variances. But we were cautious in assigning reasonable admissible intervals, so as not to compromise our ability to represent a wide range of patient-specific physiologies. Application of the proposed approach to large cohorts of patients will allow us to identify improved non-uniform priors.

We also note that additional information on the correlation between clinical targets would likely improve the estimation process. However, data scarcity poses severe limitations in this regard. Repeated patient-specific measurements are rarely available and data from the literature is useful in characterizing population variances rather than personalized data uncertainty. Correlation information could be used to eliminate redundant measurements from the tuning process, but for the present study we feel that such removal would prevent us from gathering useful information about possible physiological inconsistencies. Simultaneous estimation of both parameters and correlations in the clinical data is not addressed in this study and will be the subject of future work.

4.2. MCMC with the DREAM algorithm

MCMC provides a way to iteratively sample from a distribution that may not be known analytically, as in equation (2) [31]. Moreover, this distribution is not necessarily convex due to the underlying non-linear model, the selected model parameterization, and the availability of clinical targets. As a result, classical Metropolis MCMC with a fixed proposal distribution may experience slow convergence. Several strategies to adaptively modify the proposal distribution are discussed in the literature [32, 33, 34], leading to improved convergence rates. An interesting recent development, DREAM [35], combines differential evolution [36] and self adaptive randomized subspace sampling, showing improvements over other methods when sampling from heavily tailed or multi-modal distributions. Moreover, adoption of parallel Markov chains improves both the computational performance and offers better diagnostics to check convergence. Extensions of DREAM are discussed, for example, in [37] where parallel implementation in combination with a multiple-try-Metropolis strategy were used to sample from hydrologic models with up to 241 random parameters. These are the main reasons behind selecting the DREAM algorithm for our computations.

Note also that MCMC merely produces samples from a distribution (the stationary posterior distribution of the parameters) for which point-wise evaluations are available up to a constant. While the density of samples is expected to be larger on the posterior peaks, MCMC only provides a random exploration of the space of parameters, rather than a computation of the maximum of this posterior distribution. Hence, to determine a maximum a priori parameter estimate, we use Nelder-Mead optimization [38] using the parameter sample with maximum posterior value from MCMC as an initial guess.

4.3. 3D model surrogate

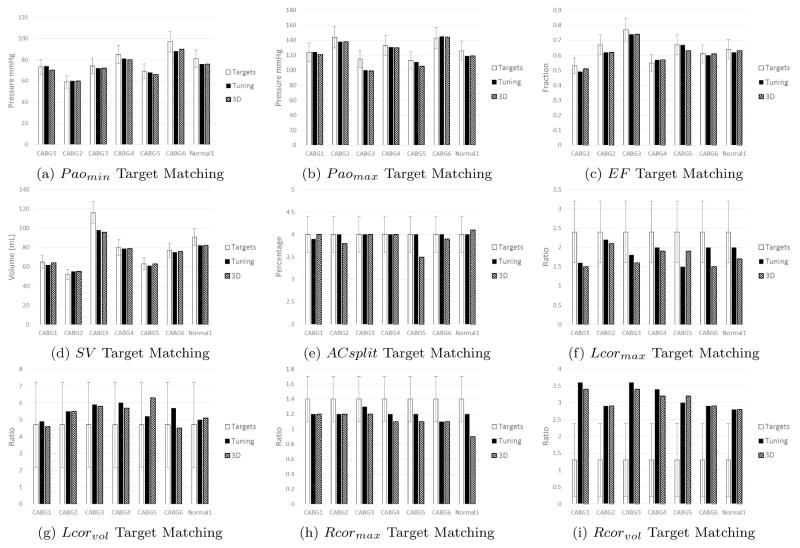
Generation of parameter samples from their stationary posterior distribution using DREAM typically requires thousands of evaluations of the coronary LPN. Running finite element simulations for each of these model evaluations is computationally intractable. To overcome this difficulty, we simplify the 3D finite element model by constructing a resistance based 0D surrogate, thus significantly reducing the computational cost for each model evaluation (from several hours to a fraction of a second). In this study, we assumed a non-compliant 3D model and negligible pressure losses due to inertia effects. A fully resistive surrogate can therefore be used to model the relationship between pressure and flow at each outlet. These surrogate resistances were selected such that the discrepancy between equivalent 0D surrogate and full multiscale simulation outputs is minimized.

Resistances for the surrogate model are obtained by first setting them equal to their respective outlet resistances defined in our coronary LPN in Section 2. The outlet resistances provide a nice starting point for determining the surrogate resistances since they ensure that the relative flow split between branches in the same system (systemic or coronary) will be preserved. To ensure this surrogate model produces output quantities consistent with the corresponding 3D simulation, we scale these surrogate resistances to minimize the discrepancy between the two models. We define two scaling factors: the first multiplies the systemic surrogate resistances and the second multiplies the coronary surrogate resistances. These scaling factors are iteratively refined until all target quantities of the surrogate simulation match within 10% of the respective 3D result (see Figure 4). The results show small differences between the two models, confirming the validity of a resistance-based approximation of the three dimensional anatomic model.

Figure 4.

Target matching across all patients for priority targets. White bars indicate targets for each patient, and the error bars indicate either the measurement uncertainty for patient-specific targets or reported standard deviations for literature targets. Black bars represent model outputs with the surrogate model, and striped bars represent model outputs from full multiscale simulations.

4.4. Parameter reduction

Identification of influential parameters and detection of their non-identifiable combinations is an important preliminary step that increases the predictive ability of numerical models. In this regard, to better understand the role played by the various LPN parameters and determine which are the most important, we used a combination of prior experience in manual tuning, analysis of structural identifiability through the Fisher Information Matrix (FIM), and the ability to learn certain parameters through Bayesian estimation.

We first used previous experience with manual tuning to identify parameters with the most significant impact on the subset of manually tuned targets, namely the patient’s blood pressure, stroke volume, flow split between systemic and coronary circulations, and the qualitative shape of the waveforms. We found that the left ventricular elastance E_lv strongly affects the stroke volume and the blood pressure to a lesser extent, while the aortic compliance C_ao has a strong influence on the difference between the systolic and diastolic aortic pressures. The coronary downstream resistance scaling factor Ram_cor has a strong influence on the flow splits, while the coronary capacitances and dP/dt_r (i.e., the intramyocardial pressure time derivative) significantly affect the shape of the coronary waveforms. Finally, the downstream systemic resistance scaling factor R_rcr strongly influences both the aortic pressure amplitude and stroke volume. We included the above parameters as important, and confirmed this assumption through the analysis of the FIM rank.

The Fisher Information Matrix is a local measure of identifiability of a system, i.e. the ability to uniquely characterize parameter combinations from the available observations [39]. A statistical model of the form (1) results in a FIM expressed as

$$\mathcal{I}(\mathbf{y})={\left[\frac{\partial \mathbf{G}(\mathbf{y})}{\partial \mathbf{y}}\right]}^T{\mathbf{C}}_d^{-1}\left[\frac{\partial \mathbf{G}(\mathbf{y})}{\partial \mathbf{y}}\right],$$ (3)

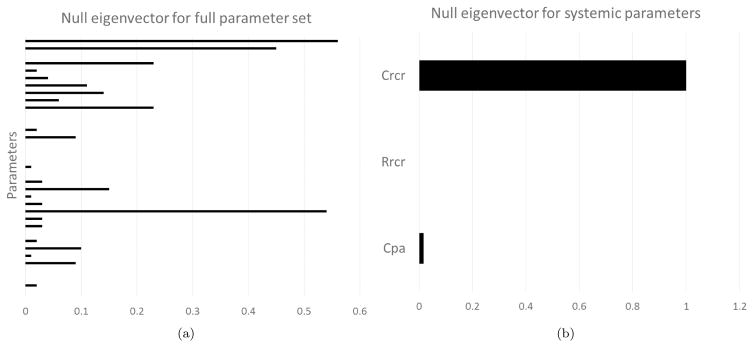
where ∂G(y)/∂y is the sensitivity matrix of local derivatives of the targets with respect to a change in the parameters (computed, in this study, using finite differences), and ${\mathbf{C}}_d^{-1}$ is the inverse diagonal covariance matrix of the clinical targets. The result ℐ (y) is a square matrix with dimension equal to the number of LPN parameters. As discussed in [39], if ℐ (y) is full rank, then the parameters are said to be locally identifiable given the available set of clinical observations. For cases of singular FIM, an analysis of the eigenvectors associated with the zero eigenvalues (i.e. null eigenvectors) can be useful in determining which parameters are not identifiable under our set of targets. In particular, a null eigenvector having a dominant component associated to a single parameter indicates that changes in this parameter do not affect the target outputs. This parameter can therefore be eliminated thus reducing the complexity of the estimation problem. An example of such a null eigenvector with a single dominant component is shown in Figure 2.

Figure 2.

(a) Null eigenvector for entire system shows multiple parameters with significant weight, making it difficult to justify elimination. (b) Null eigenvector for the systemic circulation shows C_rcr is locally unidentifiable. This is due to the fact that no clinical targets are associated with the systemic compliance, thus changing this parameter has minimal impact on the target results.

However, even after eliminating all the parameters associated with dominant components of null eigenvectors, the FIM was still found to be singular, but with non trivial null eigenvectors. In other words, non identifiable parameter combinations were still present in the LPN model but the analysis of the FIM eigenpairs was unable to suggest reparametrizations with improved identifiability.

To continue our effort in reducing the number of parameters, we examined their estimated marginal variance as a measure of global identifiability. Due to the Bayesian nature of the proposed framework, we defined the ability to learn a certain parameter by comparing the posterior and prior marginal variances as follows

$${\theta }_i=1-\sqrt{\frac{{\sigma }^2(y_i\mid \mathbf{d})}{{\sigma }^2(y_i)}}.$$ (4)

Well-learned parameters will have a much smaller variance after being conditioned to the clinical targets with θ_i being close to one. Poorly learned parameters, on the other hand, will have resulting variances that are close to their prior variance, with a corresponding θ_i close to zero. Intuitively, parameters associated with large marginal variances will likely have a limited impact on the model results selected for identification, since these parameters can take on a wide range of values, but produce results with similar posterior.

The parameter learning metrics were first observed using a synthetic set of clinical data generated from a known parameter set (hence referred to as truth). This facilitated the determination of structural measures of parameter learning by ensuring that this set of targets can be exactly represented using the LPN model. As previously performed using the FIM identifiability metric, we also observed parameter learning in separate compartments. This confirmed the results of the FIM analysis, and provided additional insight on possible unimportant parameters. Prior tuning experience, FIM analysis, Bayesian learning metrics, and qualitative knowledge of expected physiologic coronary waveforms, allowed us to determine a set of 13 parameters. This subset consistently generated excellent agreement between model outputs targets, estimated parameters close to the targets, and produced flow and pressure waveforms consistent with qualitative expectations.

A reduction in the number of parameters also generally leads to faster convergence in sampling from the stationary posterior distribution using DREAM. With 13 parameters, the framework is able to reach convergence (as monitored through the Gelman-Rubin criterion [40]) within 10,000 to 30,000 generations, depending on the patient, compared to over 100,000 generations without convergence for the full set.

5. Workflow

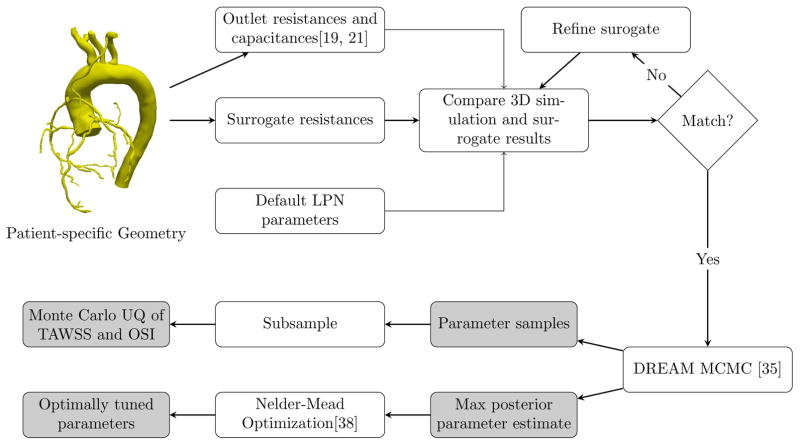
After reducing the dimensionality of our estimation problem, we tested the proposed framework on six patients with a history of coronary artery bypass graft surgery and one patient with normal coronary arteries. All patients were consented under an approved IRB protocol. We first created a surrogate 3D model for each patient through the methods described in section 4.3.

We then used DREAM to iteratively sample from the joint posterior distribution of parameters, which also performs a randomized exploration of the parameter space to search for the set of parameters characterized by maximum posterior probability. We then ran Nelder-Mead optimization [38] with an initial guess equal to the set of parameters with maximum posterior generated from DREAM, thus determining our optimal set. Finally, we compared the LPN and full 3D solutions for the optimal set of parameters and use a subset of the realizations computed from DREAM to determine the variability of the full multiscale model results. A flowchart summarizing this workflow, with references to specific algorithms used, is shown in Figure 3.

Figure 3.

Automated Tuning with Uncertainty Quantification Workflow

6. Results

6.1. Agreement between model outputs and clinical targets

The seven patients selected for this study exhibited a wide range of patient-specific targets. For example, diastolic pressures ranged from 59 mmHg to 97 mmHg, systolic pressures ranged from 113 mmHg to 143 mmHg, stroke volumes ranged from 52 mL to 116 mL, and ejection fractions ranged from 53% to 77%.

Despite these large ranges, clinical targets were closely reproduced. The average percent error between simulation results and target values for non-coronary targets across all patients is 7.6%, when the uncertainty associated with their measurement is 14.3% on average. For the literature coronary targets, the average percent error observed with the simulations is 28.4%, with the reported standard deviations in these targets being 29.0% on average. Figure 4 compares the prescribed targets, the optimal outputs for the LPN model with the surrogate, and 3D simulation results using the same parameters. Results with the surrogate closely matched the 3D simulation results, showing the robustness of a resistive surrogate in mimicking a computationally expensive 3D model with rigid walls. The resulting coronary waveforms for the analyzed patients using optimal parameters is shown in Figure 5.

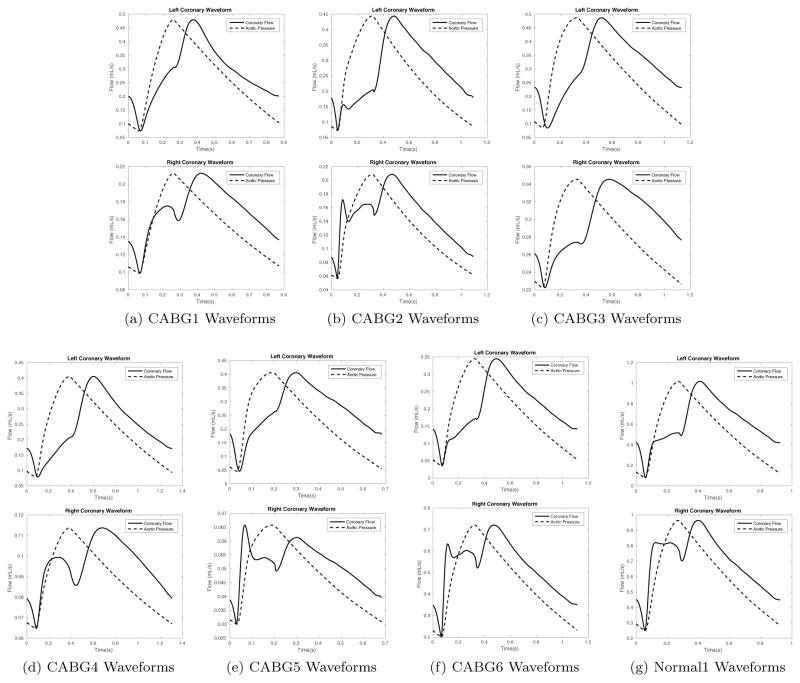
Figure 5.

Resulting coronary waveforms with optimally tuned parameters for all patients in this study. Top figures show the left coronary waveform and bottom figures show the right coronary waveform.

6.2. Optimal parameter values and associated uncertainty

Table 2 shows the optimal parameter values for each patient and their associated standard deviations, computed from the converged DREAM samples. Parameters associated with systems that are well defined by the targets are generally characterized by limited variance. In our computations, for example, the systemic circulation is well defined, with associated parameters (e.g., E_lv, C_ao, and R_rcr) showing reduced uncertainty. In other words, changing the values of these parameters produces significant changes in several targets, which strongly affects the likelihood function (2).

Table 2.

Optimal parameter values and MCMC standard deviations for each patient. Elastances E are in mmHg/mL. Elastance time derivative scaling E_lvp is in mmHg/mLs. Capacitances C are in mL/mmHg. Atrial pressure scalings Kxp are in mmHg. Resistances R are in mHgs/mL. Right coronary intramyocardial scaling dPdt_r is dimenionless.

	CABG1		CABG2		CABG3		CABG4		CABG5		CABG6		Normal1
Erv	0.25	0.11	0.20	0.03	0.84	0.21	0.88	0.25	0.27	0.44	0.79	0.26	1.00	0.25
Elv	1.52	0.18	2.59	0.39	1.91	0.27	1.66	0.19	3.79	3.27	2.11	0.24	1.77	0.23
Elvp	5.15	0.94	7.30	1.41	4.72	1.22	4.21	0.85	13.8	4.22	6.23	2.07	6.05	1.07
Cao	0.94	0.16	0.49	0.06	2.41	0.35	1.17	0.20	1.00	0.52	0.99	0.42	1.38	0.27
Kxpra	16.9	4.46	3.52	4.52	1.73	1.46	8.91	4.80	1.06	5.50	1.67	3.98	1.60	1.75
Kxpla	10.4	0.90	11.3	2.70	7.49	1.76	8.75	0.94	7.35	2.37	5.72	1.84	8.34	1.05
Ram	1.06	0.47	2.21	0.32	0.62	0.25	1.05	0.30	1.28	1.61	1.75	0.79	1.67	0.28
Caml	0.33	4.92	2.12	4.90	0.87	1.66	0.66	2.07	0.74	3.37	0.51	6.72	1.19	1.75
Cal	0.18	3.72	0.08	0.07	0.36	3.72	0.33	2.95	0.02	1.78	0.14	7.74	0.75	0.25
Camr	1.52	5.56	1.16	5.59	14.4	5.31	2.79	5.62	1.57	5.91	1.14	5.47	1.06	5.77
Car	0.19	0.14	0.08	0.04	0.46	0.12	0.24	0.11	0.09	0.15	0.55	0.24	0.98	0.20
Rrcr	1.21	0.08	1.89	0.12	0.95	0.07	1.61	0.11	0.93	0.06	1.62	0.11	1.06	0.07
dPdtr	0.54	0.14	0.54	0.11	0.52	0.12	0.52	0.13	0.56	0.14	0.52	0.14	0.56	0.12

Other parameters are instead characterized by significant uncertainty, most notably Kxp_ra, Cam_l, Ca_l, and Cam_r. The right atrial parameter Kxp_ra shows significant uncertainty across all patients, a direct result of the uncertainty in the right atrial pressure target measured through echocardiography [24]. This parameter represents the slope of the passive right atrial pressure curve, which is generally small. Thus a variation in this parameter is likely to have a limited effect on the mean right atrial pressure target. Finally, all the other parameters with high uncertainty govern coronary flow.

6.3. Variability in multiscale model predictions

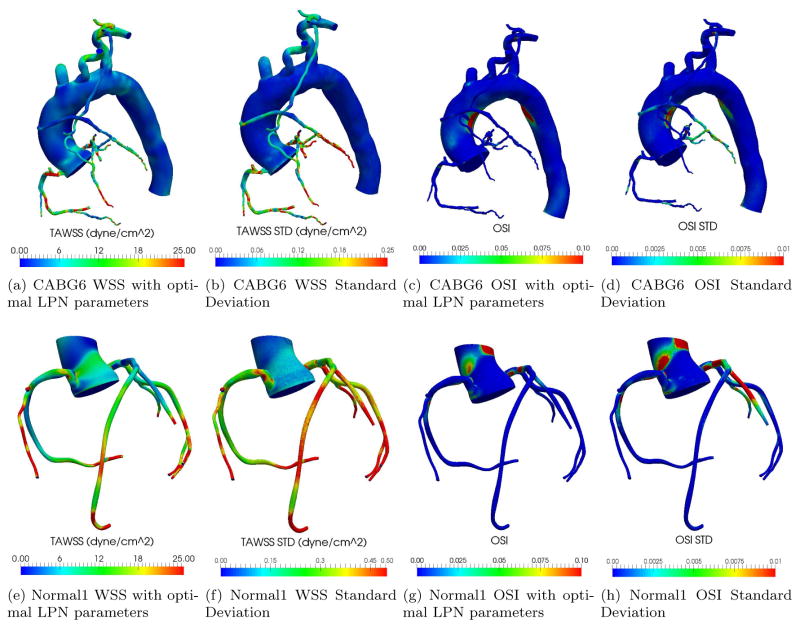
The ability to learn the distributions of LPN model parameters from uncertain clinical data enables one to evaluate the corresponding uncertainty in the hemodynamic indicators predicted in the 3D simulation model, e.g., spatial distributions of pressures, velocities, shear stresses, oscillatory shear index, etc. This is shown in Figure 6, where the optimal time averaged wall shear stress (TAWSS) and oscillatory shear index (OSI) are illustrated together with their standard deviations, for a representative CABG patient and a normal control.

Figure 6.

Multi-scale simulation results (optimal parameters and standard deviations) for CABG6 and Normal1.

A Monte Carlo estimator of the standard deviations was computed from the population average for TAWSS and OSI across 50 multiscale simulations associated with 50 parameter sets of significant posterior, sub-sampled from those generated by DREAM. TAWSS and OSI were selected due to the difficulty of measuring these quantities in vivo, and their effect on endothelial function and phenotype (see, e.g., [2]).

We also verified that the standard deviations of the LPN model parameters from the selected 50 samples were compatible with those of all the samples generated using DREAM. The average percent difference was found to be equal to 6.92% for CABG6 and 14.05% in Normal1, showing adequate agreement.

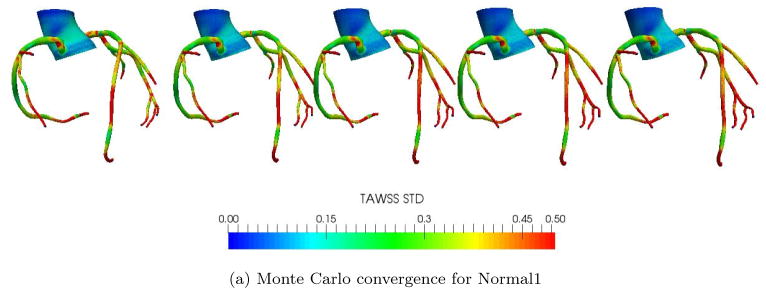
We also checked the convergence in the standard deviation of the result quantities (WSS, OSI, etc.) as computed through their Monte Carlo estimate. It is well known that the Monte Carlo estimate of the mean has a standard deviation proportional to ${\sigma }_T/\sqrt{n}$, with σ_T the true standard deviation and n the number of samples. To verify convergence, we compared the standard deviations for the TAWSS using the first 10, 20, 30, 40, and 50 samples respectively. Figure 7 illustrates the TAWSS standard deviation for both the CABG6 and Normal1 patients, showing little noticeable change in the distributions between 40 and 50 samples.

Figure 7.

Convergence of 3D Monte Carlo approximations for standard deviations in TAWSS

The Monte Carlo standard deviations for TAWSS and OSI are one order of magnitude smaller than their optimal estimates, confirming the reliability of the multi-scale predictions of these quantities. This is justified by their strong link with the mean coronary flow, which in turn is strongly influenced by the value of R_am. As reported in Table 2, the uncertainty in this parameter is limited, resulting in low uncertainty in the TAWSS and OSI.

7. Discussion and Conclusion

This study presents a framework for assimilation of non-invasive clinical data and associated uncertainty in multiscale models of the coronary circulation. The proposed framework overcomes the problems of manual tuning by automatically determining an optimal parameter set that produces results consistent with patient data. Across the six CABG patients and one normal control, the average percent error between simulation results and targets is 7.6% for patient-specific targets and 28.4% for literature coronary targets, which is within their expected uncertainties. This approach also enables quantification of confidence in the multiscale predictions (e.g., wall shear stress, oscillatory stress index, etc.) that are known to play a role in endothelial response. We have shown the standard deviation in the multiscale prediction of these quantities to be one order of magnitude less than their optimal estimates, confirming the reliability of these simulations in the presence of clinical data uncertainty.

Although the patient-specific targets agreed well with the model results as shown in Figures 4 (a) to (e), coronary targets from literature could not be matched equally well. Specifically, the right coronary volume ratio illustrated in Figure 4 (i) showed poor matching across all patients. These targets are typically associated with large variances due to both measurement uncertainty and population variability, and therefore penalized when evaluating the likelihood in (2). In other words, agreement of coronary targets is penalized with respect to the other patient specific targets due to their larger variance.

Another possible explanation for the mismatch is that our coronary LPN is unable to hit this target exactly due to the way we model intramyocardial pressure in the right coronaries. Since the right coronary arteries perfuse both sides of the heart, the choice of intramyocardial pressure for the right coronaries is not well defined. In our model, we scale down the left ventricular pressure and apply it as the intramyocardial pressure for the right coronaries. This scaling factor is one of the parameters in the LPN, and ranges from 0.5 to 1.0. This suggests that additional data on right coronary flow would be beneficial in improving our model to capture this phenomena accurately. Another possible reason for this inconsistency is that this target quantity is very sensitive to how systole and diastole are defined. In our literature review, the criterion used to identify the start of systole and diastole is often omitted, and it might differ from the definition used in our study. We defined the start of systole to be when the mitral valve closed, and the start of diastole to be when the aortic valve closed.

Overall, the computed optimal coronary waveforms were qualitatively consistent with coronary waveforms reported in the literature [41, 46, 47, 30], i.e., left coronary waveforms were characterized by almost no flow in systole and a large diastolic component, and right coronary waveforms exhibited double peaks in systole and diastole, as shown in Figure 5. However, even among these sources [41, 46, 47, 30], there is variability in the reported shape of the right coronary waveform. This again suggests that more data on right coronary flow needs to be collected to improve predictions. But until there is a way to reliably and routinely obtain patient-specific coronary flow data non-invasively, we must be satisfied with waveforms that are qualitatively consistent with previously reported shapes.

A good degree of robustness is observed under varying availability of clinical targets. For example, the absence of regurgitation in the tricuspid valve prevented max(P_rv − P_ra) to be measured for Normal1 and CABG6. As shown in Table 2, this did not significantly alter the parameter statistics compared to those obtained from the other patients (where this target quantity was available), confirming the applicability of the proposed framework to patients for whom limited imaging data prevent acquisition of low priority targets (i.e., those with ω_i > 1.0 in Table 1).

The physiological consistency produced by the optimal set of parameters can be improved by adding clinical or literature data, especially patient-specific targets for the coronary flow. Improvements in echo-Doppler technology and availability of literature studies with large patient populations will likely increase the number of targets that could be considered by the proposed approach. This may expand the number of identifiable parameters, providing more flexibility for this framework to more closely represent patient-specific physiology. Inclusion of invasive measurements, such as catheter or flow wire data, could also provide additional patient-specific measurements that would constrain the coronary parameters and would reduce the need for literature data. However, only non-invasively obtained targets were considered for this study, to highlight its use for non-invasive assessment.

A key assumption in this study was the use of rigid vessel walls. Vessel walls are known to be compliant structures characterized by finite speed pressure wave propagation [41]. Fluid-structure interaction (FSI) simulations have been adopted by several research groups [42, 43, 44], but construction of a robust compliant 3D model surrogate for tuning poses challenges that will be addressed in future work. We also note that this study only considers uncertainty in the clinical measurements used to tune boundary conditions. We observed small uncertainty in the multiscale simulations because the key LPN parameters are characterized by small variance (e.g. R_am). Uncertainty also exists in the medical images, which leads to uncertainty in the geometry of the 3D model [45]. There is also variability in the physiologic state of the patient that is not accounted for, especially with mild exercise and daily activity. In the case of FSI, there is also uncertainty in the vessel wall material properties. These all lead to additional uncertainties in the 3D results, and the framework presented here is general enough to include these additional sources in the future.

The current study focused on patients with a history of coronary artery bypass surgery. Applying the same methodology to patients with obstructive coronary artery disease who have not undergone bypass surgery and to patients with other types of coronary artery pathology (i.e. Kawasaki Disease) is also planned.

Highlights.

• A framework is presented for automated tuning of lumped parameter network boundary conditions in cardiovascular simulations

• An automated Bayesian approach is employed, achieving excellent agreement with clinical targets

• The method is demonstrated using patient specific data for 6 coronary bypass patients and one normal

• Uncertainties are propagated to 3D simulation results to demonstrate success of the method in a multiscale framework.