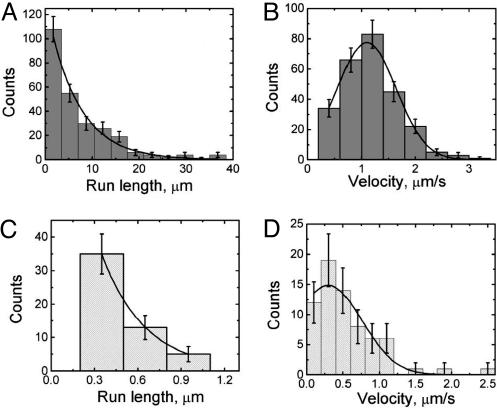
Fig. 2.

Parameters of capsid motion during entry. Histograms of the processivities and velocities of retrograde motion during entry are shown in A and B. A similar analysis of the minor anterograde component is shown in C and D. The distribution of minus-end run lengths (A) is reasonably modeled by a single decaying exponential functional form with a decay length of 6.7 ± 0.6 μm (χ² = 1.09; df = 5). Note that there could be a short (undetected) population of runs, as our spatial and temporal resolution does not permit us to accurately resolve short runs (less than ≈400 nm in length). The distribution of minus-end velocities, calculated by dividing the spatial run length by its temporal duration (B), is well modeled by a Gaussian functional form centered at 1.10 ± 0.03 μm/s and a width of 1.1 ± 0.05 μm/s (χ² = 0.52; df = 3). The distribution of plus-end runs (C) seems reasonably described by a single decaying exponential functional form with a decay length of ≈0.3 μm, but this result should be viewed as an estimate only, because many of the short runs are likely below the limit of our current resolution (a meaningful χ² value could not be determined due to these limitations). Similarly, our data suggest that the distribution of plus-end velocities (D) is reasonably modeled by a Gaussian functional form centered at 0.30 ± 0.16 μm/s and a width of 0.92 ± 0.28 μm/s. Error bars are expected uncertainty, assuming Gaussian statistics for all graphs.