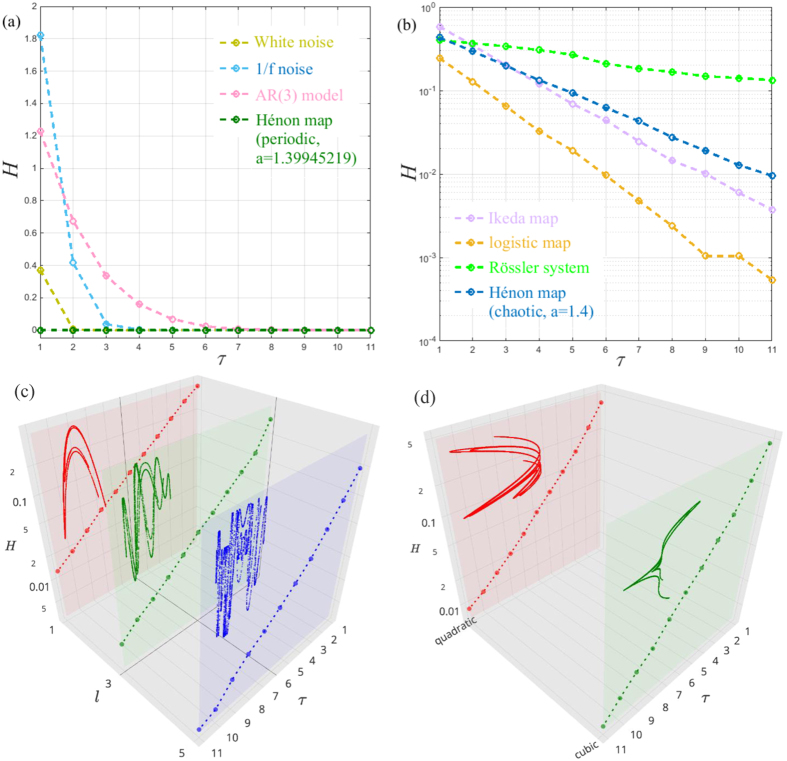
Figure 2.
The entropy growth rate H of a τ-order aggregate network as a function of the order τ for (a) White noise, 1/f noise, AR(3) model sn = 0.8sn−1 − 0.5sn−2 + 0.7sn−3 + εn (εn is generated from white noise), and the Hénon map: 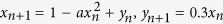 and (b) Chaotic time series (i.e., the Hénon map, the Ikeda Map: xn+1 = 1 + 0.9 (xncostn − ynsintn), yn+1 = 0.9 (xnsintn − yncostn), where
and (b) Chaotic time series (i.e., the Hénon map, the Ikeda Map: xn+1 = 1 + 0.9 (xncostn − ynsintn), yn+1 = 0.9 (xnsintn − yncostn), where 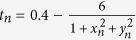 , the logistic map: xn+1 = 4xn(1 − xn), and the Rössler system:
, the logistic map: xn+1 = 4xn(1 − xn), and the Rössler system: 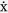 = −(y + z),
= −(y + z),  = x + 0.2y,
= x + 0.2y, 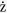 = 0.2 + z(x − 5.7)). Note that here we choose the partition N = 2500, 1600, 900, 100 for the Hénon map, the Ikeda Map, the logistic map, and the Rössler system, respectively. The entropy growth rate H as a function of the order τ for the Hénon map in chaotic regime for (c) different time delays l and for (d) quadratic and cubic nonlinear transformations of the phase space. The planar insets show the corresponding phase portraits.
= 0.2 + z(x − 5.7)). Note that here we choose the partition N = 2500, 1600, 900, 100 for the Hénon map, the Ikeda Map, the logistic map, and the Rössler system, respectively. The entropy growth rate H as a function of the order τ for the Hénon map in chaotic regime for (c) different time delays l and for (d) quadratic and cubic nonlinear transformations of the phase space. The planar insets show the corresponding phase portraits.