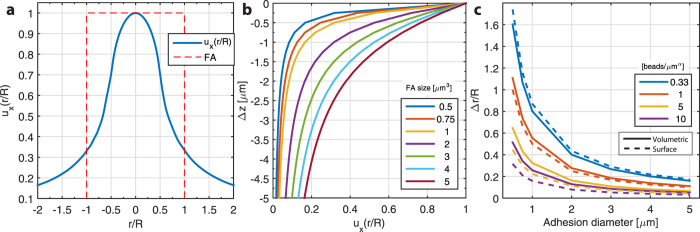
Figure 8. Analytical investigation of the displacements induced by an applied surface traction and the average distance from the adhesion center to the nearest bead.

(a) Cross-section of an in-plane displacement footprint (u_x(r/R); blue line) that results from a uniform traction T_x on a circular adhesion (red dashed line) as a function of relative distance to the center of the adhesion (r). The displacement can be described by a long-range Bessel function whose shape is invariant to the radius of the focal adhesion (R). (b) Normalized displacement magnitude as a function of depth from the surface (z = 0) for different focal adhesion sizes. For small focal adhesions, the displacement magnitude drops rapidly and therefore the bead displacement within the volume of the substrate (z < 0) is only a fraction of the displacement on the surface. (c) Analytical result of the average distance from the center of a focal adhesion to the nearest bead location (Δr), normalized to the radius of the adhesion (R). The results are shown for four different bead densities and the two bead distributions (solid line: volumetric distribution; dashed line: Beads confined to the surface of the substrate).