To the Editor:
North et al. (2002) discussed the estimation of a P value on the basis of computer (i.e., Monte Carlo) simulations. They emphasized that such a P value is an estimate of the true P value. This is essentially their only point with which we agree. The letter from North et al. is more likely to confuse than enlighten.
Consider an observed test statistic, x, that under the null hypothesis follows some distribution, f. Let X be a random variable following the distribution f. We seek to estimate the P value, p=Pr(X⩾x). Let y1,…,yn be independent draws from f, obtained by computer simulation. Let r=#{i:yi⩾x} (i.e., the number of simulated statistics greater than or equal to the observed statistic). Let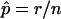 
and 
.
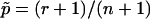North et al. (2002) stated that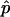 
is “not strictly correct” and that 
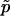is “the most accurate estimate of the P value.” They further called 
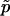“the true P value.”
We strongly disagree with this characterization. First, minor differences in P-value estimates on the order of Monte Carlo error should not be treated differently in practice, and so it is immaterial whether one uses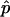 
or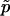 
. Second, 
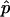is a perfectly reasonable estimate of p. Indeed, in many ways 
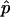is superior to 
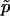. Given the observed test statistic, x, r follows a binomial (n,p) distribution, and so 
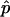is unbiased, whereas 
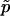is biased. (The bias of 
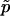is (1-p)/(n+1).) Further, 
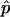has smaller mean square error (MSE) than 
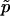, provided that p<n/(1+3n)≈1/3. (The MSE of 
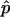is p(1-p)/n, whereas that of 
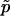is (1-p)(np+1-p)/(n+1)2.)
These results are contrary to those of North et al. (2002) because they evaluate the performance of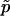 
under the joint distribution of both the observed and Monte Carlo data, whereas we prefer to condition on the observed value of the test statistic. Evaluating P-value estimates conditionally on the observed data is widely accepted when the estimation is performed via analytic approximations.
Regarding the question of how many simulation replicates to perform, we recommend consideration of the precision of the estimate,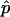 
, using the properties of the binomial distribution, rather than adherence to a rule such as r⩾10. Standard statistical packages, such as R (Ihaka and Gentleman 1996), allow one to calculate a CI for the true P value and to perform a statistical test, such as whether the true P value is <.01.
References
- Ihaka R, Gentleman R (1996) R: a language for data analysis and graphics. J Comp Graph Stat 5:299–314 [Google Scholar]
- North BV, Curtis D, Sham PC (2002) A note on the calculation of empirical P values from Monte Carlo procedures. Am J Hum Genet 71:439–441 [DOI] [PMC free article] [PubMed] [Google Scholar]