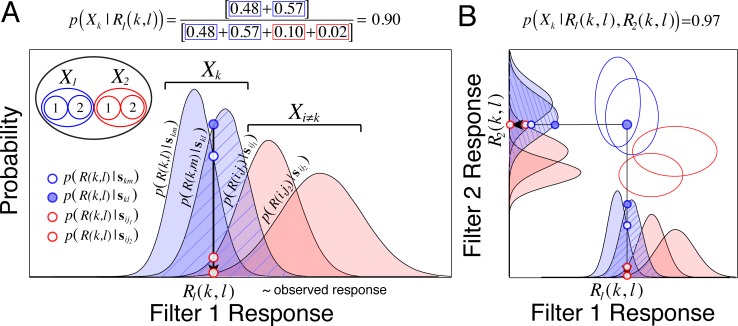
Fig 3. Relationship between filter response distributions, the likelihood, and the posterior probability.

A Hypothetical one-dimensional conditional response distributions from a single filter (receptive field). Each distribution represents noisy filter responses to each stimulus in the training set. Blue distributions represent the filter response distributions for the two stimuli having the first latent variable value. Red distributions respresent the response distributions to the two stimuli having the second (i.e. incorrect) value. The striped blue distribution corresponds to the distribution of responses to the current stimulus s_kl which, in this case, has the first value of the latent variable. The solid blue circle represents the likelihood that a random observed response R₁(k,l) was elicited by stimulus s_kl the stimulus that actually elicited the response. The open blue circle represents the likelihood that the same response was elicited by stimulus s_km, the other stimulus having latent value X_k. The sum of these stimulus likelihoods represents the likelihood that the observed response was elicited by a stimulus having latent variable value, X_k. The open red circles represent the likelihoods that the observed response resulted from the two stimuli having value X_{i ≠ k} (i.e. from stimuli with the incorrect latent variable value). The posterior probability (Eq 5) of the correct latent variable value (i.e. the latent variable value X_k corresponding to stimulus s_kl) is given by the sum of the likelihoods for within-level stimuli normalized by the sum of all likelihoods; the posterior probability distribution for this hypothetical case is shown in the next figure. Confusions between stimuli with the correct latent variable value increase the posterior probability of the correct level by contributing to the numerator (blue-boxed entries in the equation above figure panel). Confusions between correct and incorrect levels decrease the posterior probability of the correct level by contributing to the denominator (red-boxed entries in equation above figure panel). B Two-dimensional (i.e. two filter) case, under the assumption of independent response noise (note how the noise ellipses are aligned with the axes of response space). The second filter should help increase performance by selecting for useful stimulus features that the first filter does not.