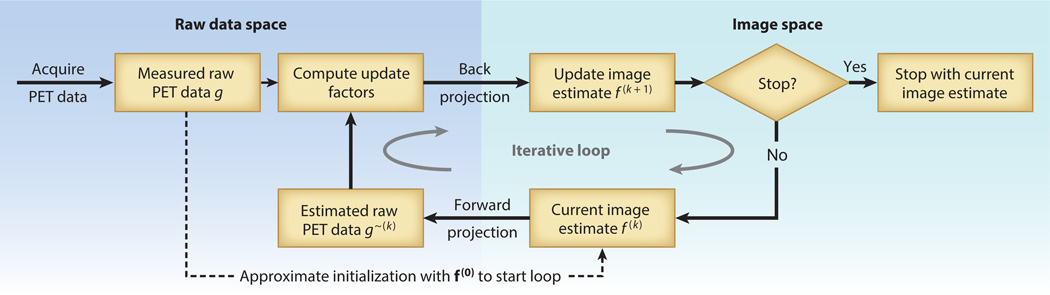
Figure 6.

General process for iterative tomographic image reconstruction. A key characteristic is the alternation back and forth between (left) the data space and (right) the image space. The process starts with the raw data acquired from positron emission tomography (PET) and an initial estimation of the reconstructed image, f⁽⁰⁾, which can be derived from the acquired data, by assuming a uniform distribution, or by another method. The first image estimation is projected into the raw data space (i.e., it is a forward projection that simulates the data-acquisition process), and the result is compared with the measured PET data. Differences are used to calculate updates, which are projected back into the image space (i.e., back projection is the adjoint operation to forward projection). This produces an updated image estimate, f⁽¹⁾. The process is repeated until the difference in estimates of sequential images reaches a convergence criteria previously defined, or a preset number of iterations occurs. Although several hundred variations of iterative algorithms have been proposed, common approaches are now used.