Abstract.
A database of retinal fundus images, the DR HAGIS database, is presented. This database consists of 39 high-resolution color fundus images obtained from a diabetic retinopathy screening program in the UK. The NHS screening program uses service providers that employ different fundus and digital cameras. This results in a range of different image sizes and resolutions. Furthermore, patients enrolled in such programs often display other comorbidities in addition to diabetes. Therefore, in an effort to replicate the normal range of images examined by grading experts during screening, the DR HAGIS database consists of images of varying image sizes and resolutions and four comorbidity subgroups: collectively defined as the diabetic retinopathy, hypertension, age-related macular degeneration, and Glaucoma image set (DR HAGIS). For each image, the vasculature has been manually segmented to provide a realistic set of images on which to test automatic vessel extraction algorithms. Modified versions of two previously published vessel extraction algorithms were applied to this database to provide some baseline measurements. A method based purely on the intensity of images pixels resulted in a mean segmentation accuracy of 95.83% (), whereas an algorithm based on Gabor filters generated an accuracy of 95.71% ().
Keywords: vessel extraction, vessel segmentation, image processing, retina, diabetes, fundus image database
1. Introduction
In the UK, eligible diabetic patients take part in a diabetic retinopathy (DR) screening program run by the National Health Service (NHS). The aim of such a screening program is not only to detect DR, but also to treat it at an appropriate stage.1 The introduction of systematic screening has been shown to improve the cost effectiveness of DR detection and treatment.2 However, the number of people suffering from diabetes continues to increase, thereby increasing the workload within existing DR screening programs.3 It is estimated that worldwide by 2025 the number of diabetics will have increased by 122% compared to levels in 1995. That is 300 million diabetics in 2025 compared to 135 million in 1995. In the UK, the prevalence of diabetes increased by 54% between 1996 and 2005, whereas the incidence increased by 63% in the same period.4 More recently, the annual report of the NHS revealed that between April 2011 and March 2012, the number of patients who were offered screening increased by 4.7%, whereas the number of people actually screened increased by 6.8% compared to the same period in the previous year.5
Computer-assisted screening could help to highlight to retinal image graders images, or image regions, containing pathologies and abnormalities not easily detected otherwise.6 As impaired oxygen supply can negatively affect the health of the retina, automatically extracting the retinal vasculature is an important tool for any computer-assisted diagnosis. For example, the automatic extraction of retinal surface vessels can be used to measure vessel diameter7 and vessel tortuosity.8 Changes in tortuosity have been linked to various diseases including diabetes,9 ischemic heart disease,10 and glaucoma.11 Glaucoma has also been linked to changes in vessel diameter.12 Moreover, the measurement of vessel diameter has been shown to provide additional predictive information on the progression of DR.13
There is a large potential for computer-assisted diagnosis in DR screening programs, including the use of automatic image processing algorithms, due to the increasing number of diabetics regularly screened. Before such algorithms can be implemented in a clinical setting, their accuracy needs to be verified. Several fundus image databases have been made publicly available for exactly this reason, allowing a comparison of the performance of various algorithms on the same dataset. Such databases exist for automatic grading of DR and risk of macular edema (the MESSIDOR database14), detection of DR lesions (the DIARETDB115 and the ROC microaneurysm set database16), for the calculation of retinal vessel width (the REVIEW17 and the VICAVR database18), and for automatic vessel extraction (DRIVE,19 STARE,20 and ARIA21 databases).
The largest database for vessel extraction, the ARIA database consists of138 images taken either from healthy subjects, diabetics, or from patients with age-related macular degeneration (AMD). All of these images were collected with a Zeiss FF450+ fundus camera with a 50-deg angular field, or field of view (FOV). The STARE database consists of 20 fundus images, half of which were taken from healthy subjects. These images were all taken with a TopCon TRV-50 fundus camera at 35-deg FOV. In contrast, the 40 images of the DRIVE database were all taken from diabetics with a 45-deg FOV setting using a Canon CR5 nonmydriatic fundus camera. Only seven of the DRIVE images show any signs of DR.
Within each of these databases, the fundus images were taken with the same fundus camera in the same setting. Furthermore, the image resolutions (ARIA: , DRIVE: , and STARE: ) are significantly smaller than the image resolutions of the fundus images currently acquired in DR screening programs across the UK. This is true even for the more recent DIARETDB1 and MESSIDOR databases that contain higher resolution retinal images (1.7 to 3.5 megapixels). Currently, the NHS Diabetic Eye Screening Program recommends a range of fundus cameras, most of which have resolutions in the order of 15.1 megapixels (e.g., the Cannon CR-2 with the Canon EOS digital camera).22 Trucco et al.6 noted that image resolution can have a large effect on the performance of vessel extraction algorithms.
The main aim of this paper is to make a more representative fundus image database, the diabetic retinopathy, hypertension, age-related macular degeneration, glaucoma image set (DR HAGIS) database,23 publicly available for testing of automatic vessel extraction algorithms. This database consists of 39 high-resolution images, recorded from different DR screening centers in the UK. It includes a range of different image resolutions and is made up of four comorbidity subgroups, each consisting of 10 images (one patient’s image is duplicated into two comorbidity subgroups). The comorbidities included are AMD, DR, glaucoma, and hypertension. In addition, two simple vessel extraction algorithms were tested against the ground truth images provided by an expert grader. Both algorithms produced vessel extraction results comparable to an independent human grader.
2. Materials
The DR HAGIS database is made up of fundus images that are representative of the retinal images obtained in an NHS diabetic eye screening program. Therefore, all fundus images were taken from diabetic patients attending a DR screening program run by Health Intelligence (Sandbach, UK). Since healthy subjects do not attend such screening programs, fundus images of healthy retinae are not included in this database.
The 39 fundus images were provided by Health Intelligence. All patients gave ethical approval for the use of these images for medical research. The 39 images are grouped into one of four comorbidity subgroups: glaucoma (images 1 to 10), hypertension (images 11 to 20), DR (images 21 to 30), and AMD (images 31 to 40). One image was placed into two subgroups, as this patient was diagnosed with both AMD and DR (images 24 and 32 are identical).
A total of three different nonmydriatic fundus cameras were used to capture the fundus images: Canon CR DGi (Canon Inc., Tokyo, Japan), Topcon TRC-NW6s (Topcon Medical Systems, Oakland, New Jersey), and Topcon TRC-NW8 (Topcon Medical Systems, Oakland, New Jersey). All fundus images have a horizontal FOV of 45 deg. Depending on the digital camera used, the images have a resolution of , , , , or .
Each fundus image comes with a manual segmentation of the vasculature. The surface vessels were manually segmented by an expert grader with over 15 years experience (G.R.). These manually segmented images were taken to be the ground truth when assessing the performance of the automatic vessel extraction algorithms. The ground truth images corresponding to the segmented vessel patterns were generated using GNU Image Manipulation Program (GIMP 2.8.1424). The original images were first opened in GIMP as JPEG files. Then transparent layers were overlaid on each original image and the line tool used to trace each retinal vessel. The brush size of the line tool was manually increased and decreased until the vessel diameter was matched. The brush tool in GIMP displays a target ring that is visible above the vessel and so gives a visual guide to the caliber of the brush tip. This method facilitated drawing a much smoother and solid continuous line and proved to be both visually accurate and relatively rapid, taking an expert on average 40 min per image. Throughout the process of tracing the retinal vessels, the transparent layer was turned on and off manually to allow for rapid and accurate checking and rechecking of line width. This technique could be likened to manually flicking between cells in animation to gauge if any change had taken place. Finally, any imperfections were erased pixel by pixel with the eraser tool generating an accurate and smooth representation of the underlying retinal vessels. We expect the variability between expert observers to be similar to the interobserver variability observed in the DRIVE database (accuracy of second observer in DRIVE database: 94.73%).19 Therefore, we included only one set of manually segmented images.
A mask is also provided for each fundus image. The mask image delineates the area of the fundus image that contains the FOV. Only the area within the FOV should be used to analyze the accuracy of the automatic vessel extraction methods. The mask images (M) were generated automatically. As shown in Eq. (1), the three color channels of the fundus images (red [R], green [G], and blue [B]) were added together, and a threshold value of 50 was applied to obtain a mask image. This resulted in the entire FOV being segmented as the foreground
| (1) |
3. Methods
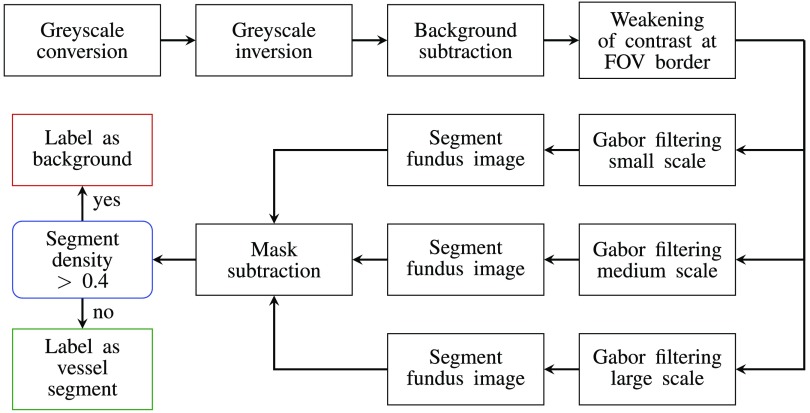
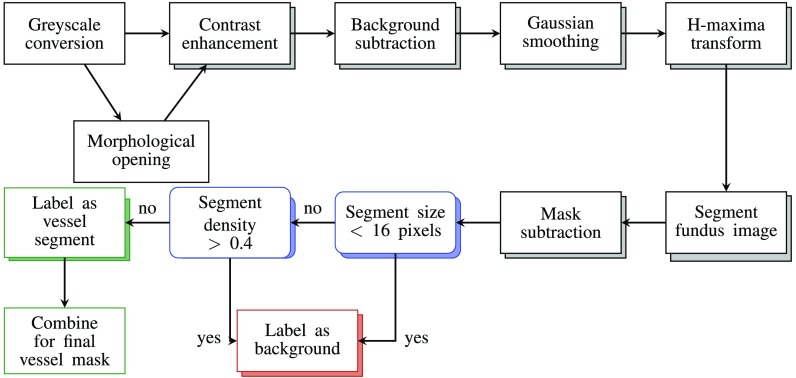
Two automatic vessel extraction algorithms were tested on these fundus images to generate some initial segmentation results. One algorithm uses only the intensity of the fundus image pixels (intensity-based) to segment vessel and nonvessel pixels, whereas the other uses both the shape and intensity of the pixel patterns (Gabor-based). These two algorithms are summarized in Figs. 1 and 2.
Fig. 1.
The Gabor filter algorithm for the automatic extraction of retinal surface vessels based on the approach of Oloumi et al.25 The RGB image is converted into grayscale, then an averaged background is subtracted to reduce the effects on any nonuniformities in illumination. The contrast between the FOV and the background is then reduced before oriented Gabor filters of up to three scales are applied to the filtered image. The outputs of the Gabor filtering stage are combined, a threshold applied before the images are postprocessed and the image pixels labeled as vessel or background (see text for details).
Fig. 2.
The intensity-based (IB) algorithm for the automatic extraction of retinal surface vessels is based on the approach of Saleh and Eswaran.26 In this approach, the RGB image is first converted into grayscale, then a morphological opening operator is applied to the grayscale image to emphasize the smaller retinal vessels. This image is processed in parallel to the original grayscale image through a series of steps designed to increase contrast and reduce the effects of uneven illumination and/or background noise. The outputs of the filtering stage are postprocessed and eventually combined, and a threshold applied before the image pixels are labeled vessel or background (see text for details).
3.1. Gabor Filter Algorithm
The Gabor filter algorithm is based on the work of Oloumi et al.25 and is summarized in Fig. 1. In short, the inverted green-channel of the RGB fundus image was used due to the high contrast between the vasculature and the retinal tissue in this color-channel.27 A background estimate, obtained by applying a median kernel, was subtracted from this green-channel image. This kernel assigns the median intensity within a neighborhood to the central pixel of this neighborhood.
Next, pixels outside the FOV were set to the average intensity of all pixels inside the FOV to reduce any border artifacts between the background and the FOV. Twelve differently oriented Gabor filters, resulting in an angular resolution of 15 deg, were then convolved with each image. This was accomplished using customized MATLAB code (MathWorks). Equation (2) shows the equation for a Gabor filter oriented at 0 deg
| (2) |
As Eqs. (3)–(5) show, only two variables are required to define the Gabor filters: the width and the length variables
| (3) |
| (4) |
| (5) |
These two variables determined the scale or size of the Gabor filters. As indicated in Fig. 1, up to three different spatial scales of Gabor filters were applied in parallel.
After applying the Gabor filters, all pixels outside the FOV were set to 0. The Gabor response images were then normalized to zero mean and unit standard deviation. A single value was applied as the threshold value to the normalized Gabor response images to generate binary masks of the vasculature. For multiscale approaches, the binary vasculature masks of each scale were summed together, and a second threshold value of was applied. To further reduce FOV border artifacts, a mask subtraction step was included. The mask used for this step was the complement of the mask image provided with the database. To this complement image, morphological dilation with a square shaped structuring element of size was applied, as defined in Saleh and Eswaran.26 After mask subtraction, a density or bounding box filtering was applied as in the final step of Saleh and Eswaran.26 The bounding box is defined as the smallest rectangle that can be fitted around an object
| (6) |
The aim of this step was to remove any larger objects that were falsely segmented as a vessel such as Drusen deposits. An object (i.e., a vessel segment) was removed if it had a density value greater than 0.4. The width, length, and the threshold value were set to account for the average image resolution of the DR HAGIS fundus images.
3.2. Intensity-Based Algorithm
The second vessel extraction method is a purely intensity-based (IB) algorithm and is a variation of the vessel extraction algorithm of Saleh and Eswaran.26 This IB algorithm, summarized in Fig. 2, consists of several steps aimed at reducing local noise and illumination variation across the fundus images, thereby increasing the contrast of the vasculature. First, the color fundus images were converted into grayscale images by using the green-channel only as in Xu and Luo 2010.27 Thereafter, the IB algorithm followed two parallel processing pathways. One included morphological opening, while the other did not. Morphological opening was applied because some of the smaller vessel segments were only segmented as such if this processing step was included in the algorithm. On the other hand, other smaller segments were only extracted if morphological opening was not applied. Therefore, each image was processed twice in parallel (once with and once without morphological opening) to increase the sensitivity of vessel detection. For the morphological opening, a disk-shaped structuring element with a radius of 5 pixels was used.
All the remaining steps were common to both processing streams. As a next step, the contrast in the grayscale images () was enhanced using Eq. (7), resulting in contrast enhanced images (CE)
| (7) |
The top hat (TH) and bottom hat (BH) functions enhanced both bright structures (TH) and dark structures (BH) within the fundus images. The square shaped structuring element was , which is significantly larger than the size of the structuring element applied to the images of the DRIVE database in Marín et al.28 (). This was due to the increased image resolution.
After enhancing the contrast, the background illumination was removed. The background illumination was estimated by applying a median kernel to image CE. The contrast enhanced image CE was subtracted from the background illumination estimate. This resulted in images with even background illumination.
In the following step, a Gaussian smoothing filter with a standard deviation of 1 pixel was applied. After Gaussian smoothing, an h-maxima transform was applied with the threshold defined as in Saleh and Eswaran.26 The h-maxima transform decreases the number of different pixel intensities,29 thereby making the selection of the threshold value used for segmenting the images [Eq. (8)] easier.
After applying the h-maxima transform, each pixel was compared to the segmentation threshold value , as defined in Eq. (8), where and are the mean and standard deviation of the h-maxima transformed image, respectively,
| (8) |
This resulted in two binary vessel masks, one from each processing pathway. Mask subtraction and bounding box filtering, as described for the Gabor filter approach, was applied to each vessel mask as a postprocessing step. However, a density threshold of 0.3 was used here. In a final step, the two postprocessed binary vessel masks were combined into a single binary vessel mask. This was achieved by summing the two postprocessed vessel maps together and applying the threshold value .
3.3. Data Analysis
The quality of segmentation was determined by the mean percentage of correctly segmented pixels within the FOV. This mean accuracy is defined in Eq. (9), where TP, TN, FP, and FN are the number of true positives, true negatives, false positive, and false negative pixels, respectively. The FOV was defined by the provided mask images. Sensitivity [Eq. (10)] was defined as the percentage of vessel pixels within the FOV segmented as such, and the specificity [Eq. (11)] as the percentage of correctly segmented background pixels (again within FOV)
| (9) |
| (10) |
| (11) |
As the majority of pixels in any extended retinal image will be background pixels, guessing that any given pixel belongs to the background will be frequently correct. To address this, we also calculated Cohens kappa () statistic, which can be interpreted as the proportion of agreement between the medical expert and the automatic algorithms after chance agreements are excluded.30 Kappa () is defined as follows:
| (12) |
where is the sum of agreements between the medical expert and the algorithm (in this case ), is the number of pixels, and is the expected frequencies of both the medical experts and the algorithm agreeing by chance. In our case, is defined as follows:
| (13) |
Several different values for the model variables were tested for their effect on the overall segmentation accuracy. The search space for these variables is discussed in Appendix A for the IB algorithm and in Appendix B for the Gabor filter algorithm. Results are given in mean ().
4. Results
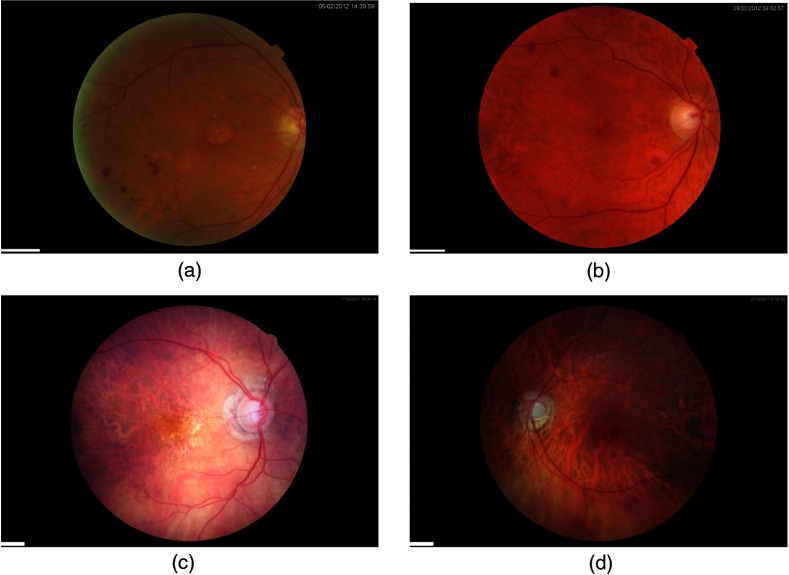
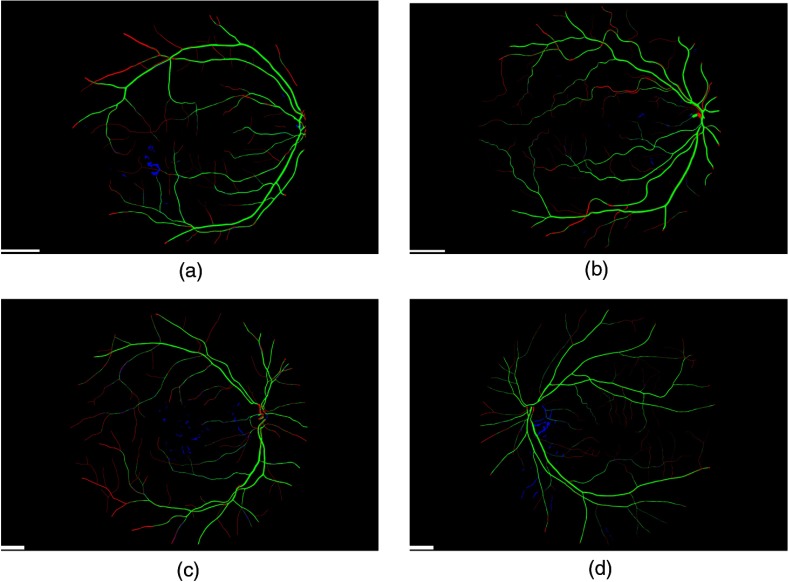
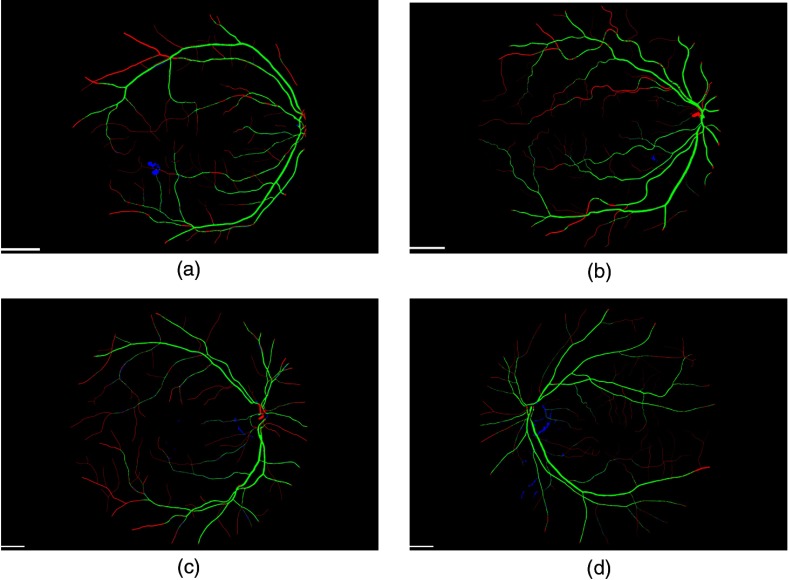
Figure 3 shows typical fundus images taken from the DR HAGIS database, one from each of the four subgroups. The corresponding segmentation results are shown in Fig. 4 for the Gabor filter algorithm and Fig. 5 for the IB algorithm. In these two figures, green pixels highlight the correctly segmented vessel pixels (true positives), red pixels are the vessel pixels falsely segmented as background pixels (false negatives), and blue pixels are the falsely segmented vessel pixels, or oversegmented pixels (false positives). Black pixels within the FOV correspond to correctly segmented background pixels (true negatives). The accuracy, sensitivity, specificity, and the kappa statistic for all 39 cases are listed in Tables 1 and 2 for the two-scale Gabor filter algorithm and IB algorithm, respectively.
Fig. 3.
Example fundus images from the DR HAGIS database. The DR HAGIS fundus image database consists of four comorbidity subgroups. Fundus images of each of these four subgroups are shown here. (a) Diabetic retinopathy, (b) hypertension, (c) AMD, and (d) glaucoma. The scale bars (short white bar in the bottom left corner of each panel) correspond to 300 pixels.
Fig. 4.
Vessel extraction with the two-scale Gabor filter algorithm. The results of the vessel extraction using the two-scale Gabor filter algorithm is shown here for the corresponding fundus images in Fig. 3. Green pixel highlight correctly segmented pixels (true positives), red pixels show those vessel pixels falsely segmented as background (false negatives), and in blue are the oversegmented, or false positive, pixels shown (when compared to the manually segmented vasculature, the ground truth). The scale bars (short white bar in the bottom left corner of each panel) correspond to 300 pixels.
Fig. 5.
Vessel extraction with the intensity-based (IB) algorithm. The results of the vessel extraction using the IB algorithm is shown here for the corresponding fundus images in Fig. 3. The color coding is identical to Fig. 4. The scale bars (short white bar in the bottom left corner of each panel) correspond to 300 pixels.
Table 1.
Accuracy, sensitivity, specificity, and kappa statistics for the two-scale Gabor filter algorithm.
| Two-scale Gabor filter algorithm | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| IN | Acc (%) | Sen (%) | Spe (%) | Kappa | IN | Acc (%) | Sen (%) | Spe (%) | Kappa |
| 1 | 97.09 | 69.15 | 98.86 | 0.72 | 21 | 95.85 | 64.10 | 98.97 | 0.71 |
| 2 | 95.73 | 63.75 | 98.38 | 0.67 | 22 | 96.04 | 66.47 | 98.61 | 0.71 |
| 3 | 95.99 | 56.81 | 99.09 | 0.65 | 23 | 94.76 | 54.80 | 98.87 | 0.63 |
| 4 | 95.78 | 59.61 | 98.90 | 0.67 | 24a | 93.84 | 54.38 | 96.50 | 0.49 |
| 5 | 96.15 | 68.38 | 98.18 | 0.69 | 25 | 95.79 | 61.72 | 97.81 | 0.60 |
| 6 | 96.33 | 65.19 | 97.88 | 0.61 | 26 | 95.31 | 60.53 | 97.84 | 0.61 |
| 7 | 95.59 | 49.57 | 99.19 | 0.60 | 27 | 94.62 | 56.60 | 97.88 | 0.60 |
| 8 | 96.02 | 63.64 | 98.53 | 0.68 | 28 | 95.21 | 65.09 | 96.84 | 0.56 |
| 9 | 96.66 | 69.73 | 98.75 | 0.73 | 29 | 95.78 | 63.45 | 98.63 | 0.69 |
| 10 | 96.17 | 60.68 | 99.26 | 0.70 | 30 | 95.13 | 50.11 | 99.23 | 0.61 |
| 11 | 96.28 | 69.83 | 98.95 | 0.75 | 31 | 95.47 | 63.08 | 99.13 | 0.71 |
| 12 | 96.15 | 67.66 | 97.46 | 0.59 | 32a | 93.84 | 54.38 | 96.50 | 0.49 |
| 13 | 96.13 | 64.34 | 96.91 | 0.42 | 33 | 95.56 | 53.15 | 98.76 | 0.60 |
| 14 | 96.40 | 65.58 | 99.10 | 0.73 | 34 | 95.01 | 60.22 | 97.90 | 0.62 |
| 15 | 95.78 | 48.45 | 99.37 | 0.60 | 35 | 95.65 | 53.53 | 97.85 | 0.53 |
| 16 | 96.37 | 54.00 | 99.16 | 0.63 | 36 | 94.97 | 51.90 | 98.91 | 0.61 |
| 17 | 95.77 | 69.31 | 98.41 | 0.73 | 37 | 96.24 | 59.28 | 98.82 | 0.65 |
| 18 | 95.55 | 54.08 | 98.93 | 0.62 | 38 | 94.80 | 38.98 | 99.12 | 0.49 |
| 19 | 96.22 | 51.54 | 98.29 | 0.53 | 39 | 96.15 | 64.57 | 98.43 | 0.67 |
| 20 | 94.40 | 47.74 | 99.12 | 0.58 | 40 | 95.89 | 66.33 | 98.76 | 0.72 |
| MEAN | 95.71 | 59.68 | 98.50 | 0.63 | SD | 0.66 | 7.38 | 0.71 | 0.08 |
Note: Acc, accuracy; IN, image number; SD, standard deviation; sen, sensitivity; spe, specificity.
Images 24 and 32 are identical.
Table 2.
Accuracy, sensitivity, specificity, and kappa statistics for the IB algorithm.
| IB algorithm | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| IN | Acc (%) | Sen (%) | Spe (%) | Kappa | IN | Acc (%) | Sen (%) | Spe (%) | Kappa |
| 1 | 97.03 | 66.73 | 98.95 | 0.71 | 21 | 95.43 | 59.77 | 98.95 | 0.68 |
| 2 | 95.70 | 62.32 | 98.46 | 0.67 | 22 | 95.69 | 61.30 | 98.68 | 0.67 |
| 3 | 95.97 | 53.37 | 99.34 | 0.64 | 23 | 94.29 | 50.10 | 98.83 | 0.59 |
| 4 | 95.54 | 53.74 | 99.15 | 0.63 | 24a | 95.22 | 48.61 | 98.36 | 0.54 |
| 5 | 95.89 | 57.50 | 98.70 | 0.63 | 25 | 95.90 | 52.23 | 98.48 | 0.57 |
| 6 | 96.38 | 49.80 | 98.68 | 0.55 | 26 | 95.43 | 50.12 | 98.73 | 0.58 |
| 7 | 95.53 | 46.73 | 99.34 | 0.58 | 27 | 94.71 | 52.68 | 98.31 | 0.58 |
| 8 | 96.03 | 59.40 | 98.86 | 0.66 | 28 | 96.45 | 58.02 | 98.53 | 0.61 |
| 9 | 96.47 | 65.38 | 98.8 | 0.71 | 29 | 95.75 | 61.06 | 98.81 | 0.68 |
| 10 | 96.18 | 59.43 | 99.37 | 0.69 | 30 | 95.37 | 49.90 | 99.51 | 0.62 |
| 11 | 96.39 | 71.45 | 98.90 | 0.76 | 31 | 95.06 | 59.89 | 99.04 | 0.69 |
| 12 | 97.06 | 62.18 | 98.65 | 0.63 | 32a | 95.22 | 48.61 | 98.36 | 0.54 |
| 13 | 97.26 | 56.42 | 98.28 | 0.48 | 33 | 95.58 | 49.42 | 99.07 | 0.59 |
| 14 | 96.22 | 63.41 | 99.09 | 0.71 | 34 | 95.24 | 55.93 | 98.51 | 0.62 |
| 15 | 96.15 | 50.43 | 99.61 | 0.63 | 35 | 96.50 | 49.70 | 98.95 | 0.57 |
| 16 | 96.44 | 51.75 | 99.38 | 0.62 | 36 | 95.32 | 52.86 | 99.20 | 0.63 |
| 17 | 95.55 | 67.44 | 98.36 | 0.71 | 37 | 96.25 | 58.07 | 98.92 | 0.65 |
| 18 | 95.94 | 56.75 | 99.14 | 0.66 | 38 | 95.25 | 43.57 | 99.25 | 0.55 |
| 19 | 96.70 | 50.93 | 98.82 | 0.56 | 39 | 95.97 | 58.94 | 98.65 | 0.64 |
| 20 | 94.65 | 47.04 | 99.47 | 0.59 | 40 | 95.02 | 53.14 | 99.09 | 0.63 |
| Mean | 95.83 | 55.83 | 98.91 | 0.63 | SD | 0.67 | 6.42 | 0.35 | 0.06 |
Note: Acc, accuracy; IN, image number; SD, standard deviation; sen, sensitivity; spe, specificity.
Images 24 and 32 are identical.
For the Gabor-filter algorithm, a single-scale, two-scale, and three-scale approach were implemented. Each scale was defined by its width and the length variables, as well by the threshold value . For the single-scale approach, the best results generated were when , , and . For the two-scale approach , , , , and , and for the three-scale approach, the Gabor filter parameters and threshold value that generated the best results were , , , , , , and .
Figure 4 shows the segmentation results for the fundus images in Fig. 3 using the two-scale Gabor filter approach. Across all 39 fundus images, the overall segmentation accuracy for the single-scale approach was 95.68% (), for the two-scale approach 95.71% (), and for the three-scale approach 95.69% (). The sensitivity was 60.10% (), 59.68% (), and 58.28% (), respectively. The specificity varied from 98.43% () for the single-scale, to 98.50% () for the two-scale and 98.59% () for the three-scale Gabor filter algorithm.
Finally, the corrected percentage of agreement measure () varied from 0.63() for the single scale, to 0.63() for the two-scale, and 0.63 () for the three-scale algorithm.
The overall mean segmentation accuracy for the IB algorithm was 95.83% () with a sensitivity of 55.83% () and a specificity of 98.91% (). The kappa statistic was 0.63 ().
5. Discussion and Conclusion
Of the three implementations of the Gabor filter algorithm, the two-scale implementation resulted in the highest accuracy. However, all three implementations (single-, two-, and three-scale) resulted in very similar overall mean segmentation accuracy, sensitivity, and specificity. Likewise, both the IB algorithm and the Gabor filter approaches resulted in a similar overall segmentation accuracy (IB algorithm: 95.83%, two-scale Gabor filter algorithm: 95.71%). Deciding whether an individual pixel belongs in a blood vessel or in the background is not always an easy task. For example, for the DRIVE database, the concurrence between two independent human observers was only 94.73%.19 If we assume similar interobserver variability for the DR HAGIS database, we can conclude that both the IB algorithm and Gabor filter approach perform as well as an expert human observer in terms of overall segmentation accuracy despite using relatively simple vessel segmentation algorithms.
The kappa statistic was similar across all our implementations (). In other words, our algorithms agreed with the medical expert far more than chance. Kappa can vary between 1 (where agreement is 100%), 0 (where the agreement is purely due to chance), and (where agreement is actually worse than chance). Previous automatic segmentation studies have employed accuracy and/or sensitivity and specificity as metrics so we include these for comparative purposes.28
The DR HAGIS database consists of four comorbidity subgroups. These subgroups highlight the typical lesions, both pathological and due to laser photocoagulation, seen in a normal DR screening program. Such lesions can make it difficult to automatically extract the retinal surface vasculature without oversegmenting the images. This trade-off between a high sensitivity and a high specificity likely explains the relatively low sensitivity of both vessel extraction approaches implemented here. However, the use of oriented Gabor filters, which detect elongated structures similar to blood vessels, did improve this somewhat.
Table 3 lists the segmentation accuracy, sensitivity, specificity, and the kappa statistic for each of the four comorbidity subgroups separately. For the Gabor filter algorithm, the single-, two-, and three-scale implementations resulted in similar accuracies, sensitivities, and specificities across all four comorbidity subgroups. However, the highest accuracies were obtained for the glaucoma subgroup (96.10% [], 96.15% [], and 96.14% [] for the single-, two-, and three-scale, respectively), followed by the hypertension subgroup (95.94% [], 95.91% [], 95.86% [], respectively). The vessel extraction for the AMD subgroup was slightly more accurate than for the DR subgroup when using any of the three Gabor filter approaches (AMD: 95.32% [], 95.36% [], 95.33% [], and DR: 95.16% [], 95.23% [], 95.23% [], respectively). Compared to the IB algorithm, the Gabor filter approaches extracted a larger proportion of the retinal vasculature, resulting in higher sensitivity across all four subgroups. The highest sensitivity was obtained for the glaucoma subgroup (62.91% [], 62.65% [], 61.13% [], for the single-, two-, and three-scale, respectively) and was lowest for the AMD subgroup (56.97% [], 56.54% [], 55.25% [], respectively). However, as shown in Table 3, the specificity was slightly lower for the Gabor filter approaches than for the IB algorithm. The highest specificity was obtained for the glaucoma subgroup (98.63% [], 98.70% [], 98.80% [], respectively), whereas the DR subgroup showed the lowest specificity (98.03% [], 98.12% [], 98.20% [], respectively). The kappa statistic varied from 0.60 () to 0.67 () across all subgroups and scales. The highest kappa statistic was obtained for the glaucoma subgroup (0.67 for all three scales).
Table 3.
The effect of diabetic retinopathy, hypertension, AMD, or glaucoma on accuracy, sensitivity, specificity, and kappa statistic for the IB and Gabor filter algorithms.
| IB algorithm | ||||||||
|---|---|---|---|---|---|---|---|---|
| Subgroup | Acc (%) | Sen (%) | Spe (%) | Kappa | ||||
| DR | 95.42 | 54.38 | 98.72 | 0.61 | ||||
| Hypertension | 96.24 | 57.78 | 98.97 | 0.64 | ||||
| AMD | 95.54 | 53.01 | 98.90 | 0.61 | ||||
| Glaucoma |
96.07 |
|
57.44 |
|
98.97 |
|
0.65 |
|
| Single-scale Gabor filter algorithm |
||||||||
| Subgroup |
Acc (%) |
Sen (%) |
Spe (%) |
Kappa |
||||
| DR | 95.16 | 59.96 | 98.03 | 0.62 | ||||
| Hypertension | 95.94 | 60.16 | 98.53 | 0.62 | ||||
| AMD | 95.32 | 56.97 | 98.34 | 0.61 | ||||
| Glaucoma |
96.10 |
|
62.91 |
|
98.63 |
|
0.67 |
|
| Two-scale Gabor filter algorithm |
||||||||
| Subgroup |
Acc (%) |
Sen (%) |
Spe (%) |
Kappa |
||||
| DR | 95.23 | 59.73 | 98.12 | 0.62 | ||||
| Hypertension | 95.91 | 59.25 | 98.57 | 0.62 | ||||
| AMD | 95.36 | 56.54 | 98.42 | 0.61 | ||||
| Glaucoma |
96.15 |
|
62.65 |
|
98.70 |
|
0.67 |
|
| Three-scale Gabor filter algorithm |
||||||||
| Subgroup |
Acc (%) |
Sen (%) |
Spe (%) |
Kappa |
||||
| DR | 95.23 | 58.68 | 98.20 | 0.62 | ||||
| Hypertension | 95.86 | 57.45 | 98.66 | 0.61 | ||||
| AMD | 95.33 | 55.25 | 98.50 | 0.60 | ||||
| Glaucoma | 96.14 | 61.13 | 98.80 | 0.67 | ||||
Note: Acc, accuracy; AMD, age-related macular degeneration; DR, diabetic retinopathy.
sen, sensitivity; spe, specificity.
Similar results were obtained with the IB algorithm. All three measures of segmentation quality were highest in the hypertensive subgroup (accuracy: 96.24% [], sensitivity: 57.78% [], specificity: 98.97% []). The glaucoma subgroup results were similar to the hypertensive subgroup for accuracy and sensitivity (96.07% [] and 57.44% [], respectively), and the mean specificity was identical (98.97% []). As with the Gabor approaches, the segmentation quality was slightly worse for the DR and AMD subgroups (accuracy: 95.42% [] and 95.54% [], sensitivity: 54.38%, [] and 53.01% [], specificity: 98.72% [] and 98.90% [], respectively). The kappa statistic varied from 0.61 () to 0.65 ().
Further improvement in vessel extraction could potentially be achieved by using an adaptive algorithm. Such an algorithm would take the dimensions of the image, the FOV, and expected retinal lesions into account, and thereby use a different set of parameters for each image or subgroup. Developing such an adaptive algorithm, however, was beyond the scope of this study.
In addition, it is possible that a neural network could improve the segmentation results of the Gabor filter algorithm. Preliminary work on the DRIVE database showed that a simple neural network discriminator did not result in a significantly more accurate segmentation of the retinal vasculature (data not shown), and this was not the main aim of this research report.
The tortuosity and diameter of retinal vessels have been shown to change in response to both ocular and cardiovascular diseases.9–12 Furthermore, impairment in ocular blood flow has been implicated in disease states such as diabetes,31–34 glaucoma,35,36 and other ocular diseases.37 It is crucial for any automatic analysis of the retinal blood vessels that the extraction of these vessels is both possible and accurate enough, particularly if the automatic analysis of the vasculature provides clinicians with additional diagnostic information. Therefore, we have put together a retinal fundus image database consisting of typical fundus images taken from a DR screening program, coupled with manual segmentations of the vascular patterns of each fundus image performed by an expert image grader. This is being made publicly available to allow others to test their automatic image processing algorithms. The images contain different comorbidities, image resolutions and were taken using different fundus and digital cameras to reflect the variability in the datasets encountered in the current NHS DR eye screening program. If an automatic vessel extraction algorithm is to be used effectively in a clinical setting, it must be able to address all these challenges.
Acknowledgments
The authors would like to thank Health Intelligence for kindly providing the fundus images that make up this DR HAGIS database. Sven Holm was funded by the Biotechnology and Biological Sciences Research Council (BBSRC).
Biographies
Sven Holm studied for his master’s and PhD degrees in neuroscience at the University of Manchester, Manchester, UK. The focus of his research was automatic vessel extraction, image registration, and imaging retinal blood flow in humans.
Greg Russell received his MPhil degree from Manchester University in 2015, while being a principle investigator for a Marie Curie funded project for retinal vascular modeling, measurement, and diagnosis (REVAMMAD). He has over 15 years of diabetic retinopathy grading experience. He has also worked in AMD, FFA, and GAC clinics. He was the interim manager for over 11 DR screening programs internationally. He is currently working for Eyenuk, a Los Angeles-based automated retinal screening company.
Vincent Nourrit received his MRes in astronomy and imaging from the University of Nice Sophia-Antipolis in 1997 and his PhD in optical communications from Telecom Bretagne in 2002. He is currently an associate professor at Telecom Bretagne where his research interests include, diffractive optical elements, retinal imaging, and the usages of virtual reality. He is a member of the Institute of Physics.
Niall McLoughlin received his BA BAI degree in computer engineering from the University of Dublin, Trinity College, in 1989, his MSc degree in computer science from the University of Dublin, Trinity College, in 1991, and his PhD in cognitive and neural systems from Boston University in 1994. He is currently a senior lecturer in the Division of Pharmacy and Optometry at the University of Manchester where his research interests include retinal and brain imaging.
Appendix A: Search Space for the IB Algorithm
Several different values were tested for most of the variables to refine the IB algorithm for vessel extraction. In a first round of refinement, the threshold value used to segment the fundus images [the 2.5 in Eq. (8)] was varied between 0.5 and 1.5 in intervals of 0.1, and between 1.7 and 2.9 in intervals of 0.2. Similarly, the size of the median filter used to obtain an estimate of the background illumination was set to either or to . The threshold value for the small object removal step was varied between 240 and 640 pixels in steps of 100 pixels. The density threshold was varied from 0.1 to 0.9 in intervals of 0.4.
After this first round of refinement, the segmentation threshold value was set to 2.5. However, the size of the median filter was set to either or to . The small object threshold value was varied from 160 to 340 pixels in intervals of 40 pixels, whereas the density threshold value was varied from 0.3 to 0.7 in intervals of 0.2.
In a third round of refinement, the median filter was set to either , , or . The small object removal threshold value was set between 80 and 160 pixels in intervals of 40 pixels. The density threshold value was either 0.1 or 0.3.
The small object removal threshold value was varied between 60 and 120 pixels in intervals of 20 pixels in a fourth round of refinement. The density threshold value was set to 0.1, 0.3, or 0.5, and the size of the median filter was varied as in the third round of refinement.
After this fourth round of refinement, 10 different Gaussian smoothing filters were tested to find the most effective Gaussian filter. Not applying a Gaussian smoothing filter did not improve the segmentation accuracy (data not shown). Furthermore, the radius for the circular structuring element used in the morphological opening step was set to either 1, 5, or 25, and the small object removal threshold value was varied between 0 and 80 pixels in intervals of 20 pixels. After refining all the variables, the effect of the different postprocessing steps on the overall segmentation accuracy was studied to develop the final IB algorithm discussed above. All other variables were defined as in the cited literature.
Appendix B: Search Space for the Gabor Filter Algorithm
Several different values for the segmentation threshold value and for width and length factors of the Gabor filters ( and , respectively) were tested to measure the accuracy of the Gabor filter algorithm. For the single-, two-, and three-scale implementation, the segmentation threshold value was varied from 1.3 to 4.0 in intervals of 0.4. For the single-scale implementation, the width factor was varied between 5 and 45 (in intervals of 5), and the length factor was varied from 0.9 to 3.3 in intervals of 0.4. For the two-scale approach, the width factor was varied between 5 and 25 (interval: 5) for the smaller Gabor filter and between 25 and 45 (interval: 5) for the larger Gabor filter. For both Gabor filters, the same length factors were used as in the single-scale implementation. For the three-scale implementation, the width factor for the small Gabor filters were set to 5, 10, or 15, the medium-sized Gabor filters were set to 20, 25, or 30, and the large Gabor filters were set 35, 40, or 45. For each of the three Gabor filters, the same length factors were tested as for the single- and two-scale implementations.
The size of the median filter used to generate the background illumination estimates was set to , as in the optimized IB algorithm. All other variables were kept as in the cited literature.
Disclosures
Conflict of Interest Statement: Dr. McLoughlin has nothing to disclose.
References
- 1.National Health Service, “English National Screening Programme for diabetic retinopathy annual report,” 2012, http://diabeticeye.screening.nhs.uk/reports (17 September 2014).
- 2.James M., et al. , “Cost effectiveness analysis of screening for sight threatening diabetic eye disease,” Br. Med. J. 320(7250), 1627–1631 (2000). 10.1136/bmj.320.7250.1627 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.King H., Aubert R. E., Herman W. H., “Global burden of diabetes, 1995–2025: prevalence, numerical estimates, and projections,” Diabetes Care 21, 1414–1431 (1998). 10.2337/diacare.21.9.1414 [DOI] [PubMed] [Google Scholar]
- 4.González E. L. M., et al. , “Trends in the prevalence and incidence of diabetes in the UK: 1996–2005,” J. Epidemiol. Community Health 63(4), 332–336 (2009). 10.1136/jech.2008.080382 [DOI] [PubMed] [Google Scholar]
- 5.National Health Service, “NHS diabetic eye screening programme 2011–12 summary,” 2013, http://diabeticeye.screening.nhs.uk/reports (17 September 2014).
- 6.Trucco E., et al. , “Validating retinal fundus image analysis algorithms: issues and a proposal,” Invest. Ophthalmol. Visual Sci. 54(5), 3546–3559 (2013). 10.1167/iovs.12-10347 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Blondal R., et al. , “Reliability of vessel diameter measurements with a retinal oximeter,” Graefe’s Arch. Clin. Exp. Ophthalmol. 249(9), 1311–1317 (2011). 10.1007/s00417-011-1680-2 [DOI] [PubMed] [Google Scholar]
- 8.Kalitzeos A. A., Lip G. Y., Heitmar R., “Retinal vessel tortuosity measures and their applications,” Exp. Eye Res. 106, 40–46 (2013). 10.1016/j.exer.2012.10.015 [DOI] [PubMed] [Google Scholar]
- 9.Sasongko M. B., et al. , “Retinal vascular tortuosity in persons with diabetes and diabetic retinopathy,” Diabetologia 54(9), 2409–2416 (2011). 10.1007/s00125-011-2200-y [DOI] [PubMed] [Google Scholar]
- 10.Witt N., et al. , “Abnormalities of retinal microvascular structure and risk of mortality from ischemic heart disease and stroke,” Hypertension 47(5), 975–981 (2006). 10.1161/01.HYP.0000216717.72048.6c [DOI] [PubMed] [Google Scholar]
- 11.Wu R., et al. , “Retinal vascular geometry and glaucoma: the Singapore Malay eye study,” Ophthalmology 120(1), 77–83 (2013). 10.1016/j.ophtha.2012.07.063 [DOI] [PubMed] [Google Scholar]
- 12.Jonas J. B., Nguyen X. N., Naumann G. O., “Parapapillary retinal vessel diameter in normal and glaucoma eyes. I. Morphometric data,” Invest. Ophthalmol. Visual Sci. 30(7), 1599–1603 (1989). [PubMed] [Google Scholar]
- 13.Klein R., et al. , “Changes in retinal vessel diameter and incidence and progression of diabetic retinopathy,” Arch. Ophthalmol. 130(6), 749 (2012). 10.1001/archophthalmol.2011.2560 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Klein J.-C., “Kindly provided by the messidor program partners,” 2004, http://messidor.crihan.fr/index-en.php (18 April 2014).
- 15.Kauppi T., et al. , “The diaretdb1 diabetic retinopathy database and evaluation protocol,” in Proc. of the British Machine Vision Conf., pp. 252–261 (2007). [Google Scholar]
- 16.Niemeijer M., et al. , “Retinopathy online challenge: automatic detection of microaneurysms in digital color fundus photographs,” IEEE Trans. Med. Imaging 29(1), 185–195 (2010). 10.1109/TMI.2009.2033909 [DOI] [PubMed] [Google Scholar]
- 17.Al-Diri B., et al. , “Review—a reference data set for retinal vessel profiles,” in 30th Annual Int. Conf. of the IEEE Engineering in Medicine and Biology Society (EMBS ’08), pp. 2262–2265 (2008). 10.1109/IEMBS.2008.4649647 [DOI] [PubMed] [Google Scholar]
- 18.Ortega Hortas M., Penas Centeno M., “The VICAVR database,” 2010, http://www.varpa.es/vicavr.html (18 April 2014).
- 19.Staal J., et al. , “Ridge-based vessel segmentation in color images of the retina,” IEEE Trans. Med. Imaging 23(4), 501–509 (2004). 10.1109/TMI.2004.825627 [DOI] [PubMed] [Google Scholar]
- 20.Hoover A., Kouznetsova V., Goldbaum M., “Locating blood vessels in retinal images by piecewise threshold probing of a matched filter response,” IEEE Trans. Med. Imaging 19(3), 203–210 (2000). 10.1109/42.845178 [DOI] [PubMed] [Google Scholar]
- 21.Farnell D. J. J., et al. , “Enhancement of blood vessels in digital fundus photographs via the application of multiscale line operators,” J. Franklin Inst. 345(7), 748–765 (2008). 10.1016/j.jfranklin.2008.04.009 [DOI] [Google Scholar]
- 22.National Health Service, “Diabetic eye screening: approved cameras and settings,” 2014, https://www.gov.uk/government/publications/diabetic-eye-screening-approved-cameras-and-settings (21 March 2016).
- 23.McLoughlin N., DR HAGIS, http://personalpages.manchester.ac.uk/staff/niall.p.mcloughlin (31 January 2017).
- 24.Gnu Image Manipulation Program, “Gnu Image Manipulation Program (GIMP),” 2014, https://www.gimp.org/downloads/ (21 March 2016).
- 25.Oloumi F., et al. , “Detection of blood vessels in fundus images of the retina using Gabor wavelets,” in 29th Annual Int. Conf. of the IEEE Engineering in Medicine and Biology Society (EMBS ‘07), pp. 6452–6455 (2007). 10.1109/IEMBS.2007.4353836 [DOI] [PubMed] [Google Scholar]
- 26.Saleh M. D., Eswaran C., “An efficient algorithm for retinal blood vessel segmentation using h-maxima transform and multilevel thresholding,” Comput. Methods Biomech. Biomed. Eng. 15(5), 517–525 (2012). 10.1080/10255842.2010.545949 [DOI] [PubMed] [Google Scholar]
- 27.Xu L., Luo S., “A novel method for blood vessel detection from retinal images,” Biomed. Eng. Online 9, 14 (2010). 10.1186/1475-925X-9-14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Marín D., et al. , “A new supervised method for blood vessel segmentation in retinal images by using gray-level and moment invariants-based features,” IEEE Trans. Med. Imaging 30(1), 146–158 (2011). 10.1109/TMI.2010.2064333 [DOI] [PubMed] [Google Scholar]
- 29.Soille P., Morphological Image Analysis, Springer, Berlin: (2004). [Google Scholar]
- 30.Cohen J., “A coefficient of agreement for nominal scales,” Educ. Psychol. Meas. 20, 37–46 (1960). 10.1177/001316446002000104 [DOI] [Google Scholar]
- 31.Hammer M., et al. , “Diabetic patients with retinopathy show increased retinal venous oxygen saturation,” Graefe’s Arch. Clin. Exp. Ophthalmol. 247(8), 1025–1030 (2009). 10.1007/s00417-009-1078-6 [DOI] [PubMed] [Google Scholar]
- 32.Hammer M., et al. , “Retinal vessel oxygen saturation under flicker light stimulation in patients with non-proliferative diabetic retinopathy,” Invest. Ophthalmol. Vis. Sci. 53(7), 4063–4068 (2012). 10.1167/iovs.12-9659 [DOI] [PubMed] [Google Scholar]
- 33.Hardarson S. H., Stefánsson E., “Retinal oxygen saturation is altered in diabetic retinopathy,” Br. J. Ophthalmol. 96(4), 560–563 (2012). 10.1136/bjophthalmol-2011-300640 [DOI] [PubMed] [Google Scholar]
- 34.Jørgensen C. M., Hardarson S. H., Bek T., “The oxygen saturation in retinal vessels from diabetic patients depends on the severity and type of vision-threatening retinopathy,” Acta Ophthalmol. 92(1), 34–39 (2014). 10.1111/aos.12283 [DOI] [PubMed] [Google Scholar]
- 35.Hardarson S. H., et al. , “Glaucoma filtration surgery and retinal oxygen saturation,” Invest. Ophthalmol. Vis. Sci. 50(11), 5247–5250 (2009). 10.1167/iovs.08-3117 [DOI] [PubMed] [Google Scholar]
- 36.Olafsdottir O. B., et al. , “Retinal oximetry in primary open-angle glaucoma,” Invest. Ophthalmol. Vis. Sci. 52(9), 6409–6413 (2011). 10.1167/iovs.10-6985 [DOI] [PubMed] [Google Scholar]
- 37.Hardarson S. H., “Retinal oximetry,” Acta Ophthalmol. 91, 1–47 (2013). 10.1111/aos.2013.91.issue-thesis2 [DOI] [PubMed] [Google Scholar]