Abstract
We investigate the problem of learning an evolution equation directly from some given data. This work develops a learning algorithm to identify the terms in the underlying partial differential equations and to approximate the coefficients of the terms only using data. The algorithm uses sparse optimization in order to perform feature selection and parameter estimation. The features are data driven in the sense that they are constructed using nonlinear algebraic equations on the spatial derivatives of the data. Several numerical experiments show the proposed method's robustness to data noise and size, its ability to capture the true features of the data, and its capability of performing additional analytics. Examples include shock equations, pattern formation, fluid flow and turbulence, and oscillatory convection.
Keywords: partial differential equations, machine learning, parameter estimation, sparse optimization, feature selection
1. Introduction
Differential equations provide fundamental models in the physical and life sciences. Many examples of partial differential equations (PDEs) exist in the physical sciences, for example Maxwell's equations for electromagnetism, Einstein's equation for general relativity, Schrödinger's equations in quantum physics and chemistry, Boltzmann's and Vlasov's equations in plasma physics, and the Navier–Stokes and Euler equations in fluid and gas dynamics. These equations are often considered essential descriptors of important physical phenomena. In the life sciences, PDEs typically describe dynamic processes such as the Keller–Segel model for chemotaxis, predator–prey equations, reaction–diffusion equations, and the Hodgkin–Huxley and FitzHugh–Nagumo models for neural excitement. PDEs also model complex behaviours in the social sciences, for example conservation laws for traffic flow, systems of equations for population dynamics, epidemic models and financial markets. The original discoveries of these equations (typically) required a grasp of mathematics, an understanding of theory, and supportive evidence from experimental data. In this work, we provide a computational approach for learning the underlying PDE that governs a particular phenomenon only using the data.
Machine learning and regression provide numerical tools to explore large datasets and learn the underlying behaviours. These methods can supply researchers with important techniques to support and augment their path to scientific discovery. Two important contributions to the discovery of physical laws from experimental data can be found in [1,2]. The main approach is to use symbolic regression in order to recover the underlying physical equations that govern the structure of the phenomena. The idea in [1,2] is to compare numerical derivatives of the experimental data with analytic derivatives of candidate functions. The regression approach balances between the efficiency of the candidate model and the accuracy of the fit. In a recent study [3], an alternative approach using sparse regression is proposed. Rather than using symbolic regression, a sequential thresholded least-squares algorithm is applied to a set of candidate functions (polynomials) in order to approximate the governing equations for a nonlinear dynamical system. The idea in [3] gives a direct approach to identifying key terms in the dynamical system within a set space of candidate polynomials. In this work, we propose a sparse optimization method for identifying the underlying PDE to a given dataset.
Sparsity plays a key role in optimization and data sciences. The L1 norm is often used as a proxy for sparsity, because it allows for the construction and implementation of feasible numerical schemes. The least absolute shrinkage and selection operator (LASSO) [4] proposed augmenting the least-squares problem, commonly used in data fitting, with the L1 norm on the unknown coefficients. The L1 norm is used to penalize the number of non-zero coefficients in order to promote coefficient sparsity. The L1 penalty formulation has yielded a rich body of research and applications. One application is in compressive sensing, which (in general) is the recovery of a signal from random measurements and results in an under-determined system of linear equations (see [5,6]). The linear system is typically solved via an L1 (or related) regularized least-squares minimization and (in some cases) can be shown to exactly recover the sparse solution [7]. Sparsity is also extremely advantageous for learning key features from datasets. One popular example is its use in dictionary learning, where one learns a sparse representation for a given dataset (typically images) while simultaneously learning the features (referred to as the dictionary) themselves (see [8,9]).
In recent years, sparsity and sparse optimization have been applied to problems in differential equations and scientific computing. Some examples include modelling multi-physics and multi-scale phenomena related to nonlinear PDEs [10–13] in the construction of basis functions for quantum mechanical models [14–16] and in reduced-order modelling of dynamic systems [17–20]. The interaction between PDEs and the L1 terms has been studied in [21–23], providing some properties of solutions.
The paper is outlined as follows. In §2, a motivating example of the proposed method is provided and its construction is detailed. The numerical method and algorithm, including the construction of the features used in the learning step, are provided. In §3, the data simulation is detailed. Several numerical experiments are presented, measuring the robustness of the method to data noise and size, the method's ability to capture the true features of the simulated data, and its capability to perform other important tasks. We end with some concluding remarks in §4.
2. Sparse reconstruction of partial differential equations
Before detailing the method and algorithm, we will derive the proposed method for a specific example.
(a). Motivation and model
Consider the problem of discovering the underlying PDE when data were obtained from the viscous Burgers’ equation:
Assume that the form of the equation is unknown to the user, and instead we consider the general form for second-order PDEs with quadratic nonlinearity (in space)
This assumption can be made by a user based on some physically relevant models related to the data/simulation. The r.h.s. can also be obtained by approximating a general second-order evolution equation ut=F(u,ux,uxx) via a second-order Taylor expansion. The PDE above can be written as the product of (u,ux,uxx)-dependent terms with fixed coefficients
| 2.1 |
This equation holds at all points (x,t) in the domain. Each of the (u,ux,uxx)-dependent terms in equation (2.1) represents a potential feature that describes the intrinsic dynamics of the data. Define the feature vectors f1(t), f2(t),…, and f10(t), by
where each time-dependent feature vector is the vectorization of the terms in equation (2.1). Specifically, each component of the feature vector fℓ(t) is the evaluation of the corresponding term from equation (2.1) at a pre-determined point in space. For example, given n spatial points, the third feature vector is defined as
The collection of feature vectors defines the feature matrix, i.e. Fu(t)=[fℓ(t)] or (explicitly)
Let V (t) be the ‘velocity’ vector, i.e.
Then for t>0, the following system of equations holds:
| 2.2 |
The terms V and F are known while the coefficients α are unknown. Note that the problem is linear in the unknown α. As the feature matrix and the velocity vector are data dependent (i.e. generated from a particular initial condition), the inverse problem (equation (2.2)) may not produce a unique solution α (for example, consider the trivial case u(x,t)=0 for all t>0). Also, because the data may contain noise, the inverse problem can be ill-posed. To deal with this ill-posedness, we will use the entire dataset along with a regularizer.
The linear system in equation (2.2) holds for all time, so we have
| 2.3 |
If the number of columns in Fu(t) is less than the number of discrete grid points in x, then both equations (2.2) and (2.3) are over-determined. In the ‘perfect’ case, where u(x,t) is exactly generated by the given PDE, the features are exact. Thus, the inverse problem can be solved directly and it may be possible to recover the correct coefficients (under some mild assumptions). However, if the data are collected from a simulation or experiment, direct solutions (for example, using the pseudo-inverse) yield the incorrect coefficients. Instead, to solve equation (2.3), we use an L1-regularized least-squares minimization
| 2.4 |
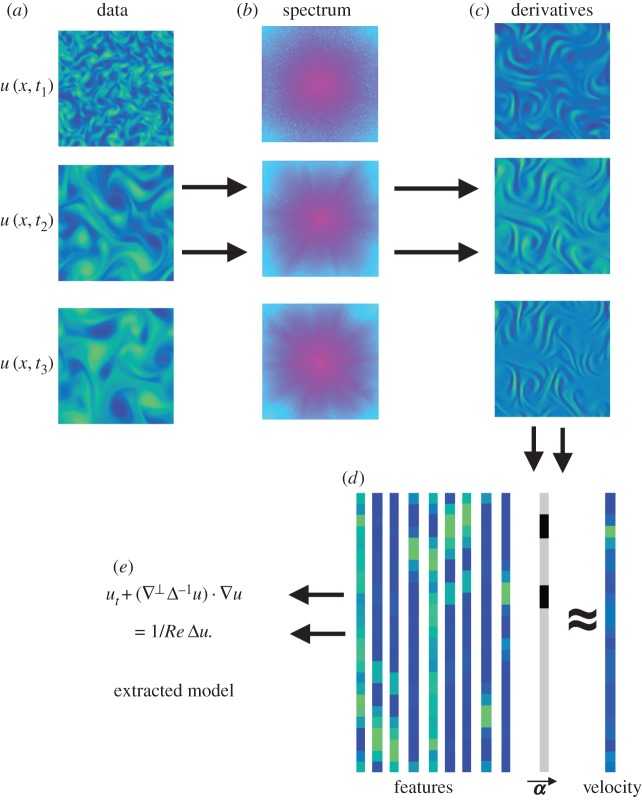
where λ>0 is a balancing parameter. The least-squares term in equation (2.4) is taken over several discrete time stamps tk. Without a regularization term, the noise makes the solution meaningless. The L1 regularization is chosen to promote sparsity in the vector α, with the modelling assumption that the underlying dynamics are governed by a few terms. A visual guide to this algorithm is provided in figure 1.
Figure 1.
Visual algorithm. The data are given as a sequence at different time stamps (a). Then, the data are converted to the Fourier domain (b) and the spatial derivatives are calculated (c). The derivatives are combined to construct features, which are then vectorized (d). An L1 optimization algorithm is used to extract the sparsity coefficients α that fit the features to the velocity. The coefficients α are unravelled to reveal the underlying model (e). (Online version in colour.)
(b). Numerical method and algorithm
Given data w(x,t) at (possibly non-uniform) grid points xj for 1≤j≤N and time stamps tk for 1≤k≤M, we approximate the underlying evolution equation wt=G(w) using the idea from §2a. In this section, we will make a distinction between the given (discrete) data w(x,t) and the computed variable u(x,t) that is generated by a particular PDE. The following steps are required to approximate the form of the evolution equation wt=G(w): first compute a numerical approximation to the spatial derivatives of w(x,t), then construct a collection of feature vectors, and lastly compute the coefficients of the terms using the sparse least-squares method.
First, we set the highest order spatial derivative expected in the model and calculate all derivatives up to that order. To demonstrate the details of this algorithm, we will focus on the two-dimensional case where w has periodic boundary conditions on a square and thus construct derivative approximations using the spectral method [24]. Note that this method can be applied to more general dimensions and that examples in §3 contain both one-dimensional and two-dimensional datasets. Setting the wavenumbers to kx=−πN/L,…,πN/L and ky=−πN/L,…,πN/L, the pth spatial derivatives are approximated using the following equations: (Dx)pw≈ifft((ikx)p fft(w)) and (Dy)pw≈ifft((iky)p fft(w)). Alternative approximations, such as finite differences or finite elements, can be used. If the data w(x,t) are very noisy, then preprocessing and/or regularization is needed to calculate the spatial derivatives (see example 3.9).
The feature vectors fℓ(t) can be found by taking polynomials of the derivative terms. The features can be determined by using the terms of a Taylor expansion and/or by collecting common terms from known models with similar behaviour. It is assumed that the number of features (i.e. the size of the feature space) is larger than the number of terms in the underlying dynamics and that the feature space includes the true terms in the underlying equations. Because the feature space is constructed using algebraic equations on the data and its spatial derivatives, the space can be arbitrarily large and redundant. Note that the features themselves are problem dependent—explicit examples are provided §3. Each feature is normalized (by dividing the feature vector by the maximum magnitude of the feature vector over all time stamps), in order to prevent biasing in the optimization. The sparse optimization problem (equation (2.4)) penalizes the magnitude of the coefficients directly, thus the approximation of the coefficients could be biased by the high variance among the magnitudes of the vectors. For example, if one of the feature vectors is arbitrarily small, then its inclusion may not be ‘costly’ with respect to the optimization. Once the feature vectors are computed and normalized, the feature matrix is constructed by appending them together column-wise: Fw(t)=[ fℓ(t)]. After the coefficients are computed, we will need to rescale them in order to invert the normalization.
The time derivative of the data wt is either given or computed numerically using finite differences. Vectorizing wt forms the ‘velocity’ vector V (t). The values of wt may be noisy due to the data acquisition process, computational error or approximation error. This method does not require any preprocessing of the velocity vector. The coefficients are found via a sparse least-squares minimization
| 2.5 |
where λ>0 is a balancing parameter. The minimizer satisfies the following inclusion relation [25]:
which can be written as
| 2.6 |
The number of equations given in equation (2.6) is equal to the number of unknown coefficients. Therefore, the size of the problem can be relatively small if the number of features is small or arbitrarily large if the feature space contains many terms. There are several ways to solve equation (2.6) in practice (see [26–30]). We use the Douglas–Rachford algorithm [31,32]. Define the two terms
The proximal operator for a functional H(x) is defined as
The proximal operators for these functions can be written as [33]
which is commonly known as the shrink operator, and
which is a regularization of the standard normal equation. The Douglas–Rachford iteration is defined by the following two-step method [32]:
| 2.7 |
where rproxγH(x)=2proxγH(x)−x. Note that the order of the operators matters, and it is typical to use the shrink operator as the second step to maintain sparsity. For γ>0 and μ∈[0,2], the iterates αk converge to the minimizer of equation (2.5). For more details on the convergence of the Douglas–Rachford algorithm, see [34,35].
The coefficients identified by equation (2.5), denoted α*, will typically have some bias due to the shrinkage function. Define the support set of the minimizer of equation (2.5), i.e. . If the restriction of the matrix onto the support set is well conditioned, we can refine the solution α* by a second optimization over all vectors with the same support
| 2.8 |
This step removes any bias in the value of the coefficients while retaining the features. Altogether, the proposed algorithm is as follows:
Partial differential equations, sparse learning algorithm
Step 1: Given w(x,t), calculate all spatial derivatives (up to some order) using the spectral method.
Step 2: Construct feature vectors via algebraic equations of the spatial derivatives. Normalize feature vectors to have maximum value 1.
Step 3: Use the Douglas–Rachford algorithm, equation (2.7), to solve the L1 least-squares problem (equation (2.5)). Extract the support of the vector.
Step 4: (Optional) If the matrix restricted to the support set is well conditioned, then refine the solution of equation (2.5) by solving equation (2.8).
Note that the normalization in step 2 must be ‘undone’ after step 4 in order to recover the actual coefficient corresponding to a particular feature. Also, to compute non-trivial solutions, the parameter λ should be in the interval ; see [36] for related work.
3. Simulation and numerical experiments
To test the method, data are simulated using an accurate method on a higher resolution grid. Then, the simulated data u(x,t) are restricted onto a coarse grid and are assigned to the variable w0(x,t). The noise-free velocity is computed by a first-order backward difference
where dt>0 is the time step. The computed velocity wt is corrupted by additive Gaussian noise, which models possible corruption in the velocity measurement or its calculation. The noisy velocity is assigned to wt. The noise level is displayed for all examples in this section by measuring the ratio between the L2 norm of the noise and the L2 norm of the data, i.e.
All features are computed using w0(xj,tk); therefore the fitting is done on a backward Euler step at each time stamp. It is worth noting that the approximations used to simulate the data and the approximation used to learn the features are not the same.
Here, we include several examples which represent various phenomena and applications. In all examples, the parameters for the Douglas–Rachford algorithm are set to: , μ=1 and the maximum number of iterations to 5000. Convergence of the iterates is achieved before the maximum iteration bound is reached.
(a). Examples and applications
Example 3.1 (viscous Burgers' equation) —
The first example is the viscous Burgers' equation
where ν>0 is the viscosity and x∈[0,1]. The data are simulated using the Crank–Nicolson method with 1024 grid points and with . The data are simulated from t∈[0,0.05]. The spectral simulation is computed in conservative form although the feature vectors will not be in conservative form. The balance parameter is fixed to λ=500.
In table 1, the feature space is made up of the terms from a third-order Taylor expansion using up to second-order derivatives. The proposed algorithm is applied to the data with various levels of noise. For all noise levels, 2.0%, 19.5% and 94.5%, the coefficients are identified to within 1% in relative error. As the noise level increases, the approximation to the coefficients stays within two significant digits. This example shows that the method seems robust to noise. Also, as all spatial derivatives are approximated using the spectral method and the features are computed via direct products, each term is not necessarily in the proper form (i.e. the features are non-conservative, non-monotone, etc.). Yet, the method is able to detect the correct features and approximate the true value of the coefficients.
Table 1.
Example 3.1: viscous Burgers’ equation. The feature space is made up of the terms from a third-order Taylor expansion using up to second-order derivatives. The coefficients are identified to within 1% in relative error. As the noise level increases, the approximation to the coefficients stays within two significant digits.
| terms | coefficients, noise=2.0% | noise=19.5% | noise=94.5% |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| u | 0 | 0 | 0 |
| u2 | 0 | 0 | 0 |
| u3 | 0 | 0 | 0 |
| ux | 0 | 0 | 0 |
| 0 | 0 | 0 | |
| 0 | 0 | 0 | |
| uux | 0.9953 | 0.9949 | 0.9948 |
| u2ux | 0 | 0 | 0 |
| 0 | 0 | 0 | |
| uxx | 0.0099 | 0.0099 | 0.0099 |
| 0 | 0 | 0 | |
| 0 | 0 | 0 | |
| uuxx | 0 | 0 | 0 |
| u2uxx | 0 | 0 | 0 |
| 0 | 0 | 0 | |
| uxuxx | 0 | 0 | 0 |
| 0 | 0 | 0 | |
| 0 | 0 | 0 | |
| uuxuxx | 0 | 0 | 0 |
In figure 2, the coefficients learned from the data with 94.5% noise (column 3 of table 1) are used to compare the original solution with the learned solution. In figure 2a is the original simulation (black, solid) using 1024 grid points and the learned solution (blue, dotted) using 256 grid points at time T=0.1 (which is well beyond the interval used in the learning algorithm). Figure 2b is the absolute value of the error between the true and learned solutions projected onto the coarse grid. The error between the original simulation and the learned solution is small in norm: the L1 error is 0.0128, the L2 error is 0.0014 and the error is 0.0200. The error between the learned solution and the original data incorporates both the error in the learned parameters and the difference between the two resolutions. The projection error (i.e. the difference between the original simulation using 1024 grid points and a simulation using 256 grid points with the exact parameters) in the various norms is: the L1 error is 0.0114, the L2 error is 0.0012, and the error is 0.0195. In figure 3, the space–time dynamics are plotted to provide a qualitative comparison between the original simulation (figure 3a) and the learned dynamics (figure 3b). This shows that the parameter estimation leads to a close approximation to the original dynamics in both quantitative and qualitative senses. The main interest here is the identification of the correct terms in the underlying dynamics and the approximation of the coefficients of the equation.
Figure 2.
Example 3.1: viscous Burgers’ equation with noise level =94.5%. In (a) is the original simulation (black, solid) using 1024 grid points and the learned solution (blue, dotted) using 256 grid points at time T=0.1. In (b) is the absolute value of the error between the true and learned solutions projected onto the coarse grid. (Online version in colour.)
Figure 3.
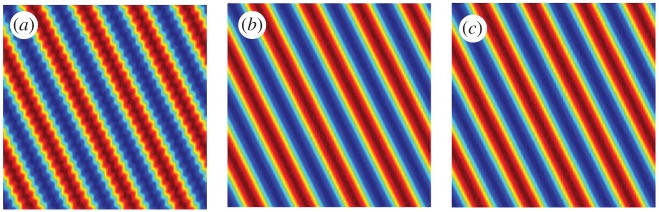
Example 3.1: viscous Burgers’ equation with noise level =94.5%. The space–time dynamics are plotted to provide a qualitative comparison between the original simulation (a) and the learned dynamics (b). This shows that the parameter estimation leads to a close approximation to the original dynamics. The horizontal axis is space and the vertical axis is time. (Online version in colour.)
Example 3.2 (inviscid Burgers' equation) —
To generate the solution to the inviscid Burgers' equation, we simulate the viscous equation with 0<ν≪1 and x∈[0,1]. The data are simulated using the Crank–Nicolson method with 1024 grid points, ν=9.8×10−4 (near the vanishing limit), from t∈[0,0.05]. The spectral method is applied to the conservative form of the PDE. The balance parameter is fixed to λ=500, as in example 3.1.
In table 2, the feature space is made up of the terms from a third-order Taylor expansion using up to second-order derivatives. The algorithm is applied to the data, with various levels of noise. For all noise levels, 1.5%, 15.0% and 73.7%, the coefficients are identified to within 2% in relative error. As the noise level increases, the identification of the correct features stays stable, while a slight decrease occurs in the approximation of the coefficients. This shows the robustness of the method to noisy data.
Table 2.
Example 3.2: inviscid Burgers' equation. The feature space is made up of the terms from a third-order Taylor expansion using up to second-order derivatives. The coefficients are identified to within 2% in relative error. As the noise level increases, the identification of the correct features stays stable. Note that the terms used in the feature space are not necessarily in the correct form (they are non-conservative, non-monotone, etc.), yet the correct coefficients are detected and resolved.
| terms | coefficients, noise=1.5% | noise=15.0% | noise=73.7% |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| u | 0 | 0 | 0 |
| u2 | 0 | 0 | 0 |
| u3 | 0 | 0 | 0 |
| ux | 0 | 0 | 0 |
| 0 | 0 | 0 | |
| 0 | 0 | 0 | |
| uux | 0.9989 | 0.9987 | 0.9972 |
| u2ux | 0 | 0 | 0 |
| 0 | 0 | 0 | |
| uxx | 0.0010 | 0.0010 | 0.0010 |
| 0 | 0 | 0 | |
| 0 | 0 | 0 | |
| uuxx | 0 | 0 | 0 |
| u2uxx | 0 | 0 | 0 |
| 0 | 0 | 0 | |
| uxuxx | 0 | 0 | 0 |
| 0 | 0 | 0 | |
| 0 | 0 | 0 | |
| uuxuxx | 0 | 0 | 0 |
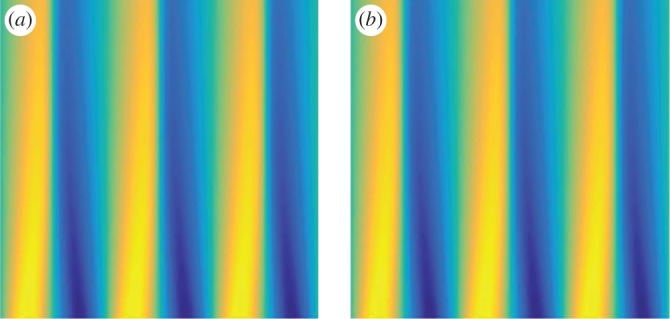
In figure 4, the coefficients learned from the data with 73.7% noise (column 3 of table 2) are used to compare the original solution with the learned solution. Figure 4a is the original simulation (black, solid) using 1024 grid points and the learned solution (blue, dotted) using 256 grid points at time T=0.1. Figure 4b is the absolute value of the error between the two solutions projected onto the coarse grid, which shows that the learned dynamics agree with the original data everywhere except at the shock. In figure 5, the space–time dynamics are plotted to provide a qualitative comparison between the original simulation (figure 5a) and the learned dynamics (figure 5b) over time. The error between the original simulation and the learned solution is small in norm: the L1 error is 0.0163, the L2 error is 0.0193 and the error is 0.2705, which also includes the projection errors (difference in grid sizes). The error is larger in example 3.2 than in example 3.1 because the solution in example 3.2 contains shocks whose locations strongly depend on the values of the coefficients in the PDE. In both examples 3.1 and 3.2, the dynamics are learned from t∈[0,0.05] but the comparisons are done at T=0.1, showing the possibility of leveraging this type of learning in order to extrapolate dynamics and predict critical events (such as shock formation).
Figure 4.
Example 3.2: inviscid Burgers' equation with noise =73.7%. Plot (a) is the original simulation (black, solid) using 1024grid points and the learned solution (blue, dotted) using 256 grid points at time T=0.1. Plot (b) is the absolute value of the error between the two solutions projected onto the coarse grid, which shows that the learned dynamics agree with the original data everywhere except at a few grid points near the shock. (Online version in colour.)
Figure 5.
Example 3.2: inviscid Burgers' equation with noise =73.7%. The space–time dynamics are plotted to provide a qualitative comparison between the original simulation (a) and the learned dynamics (b) over time. The error between the original simulation and the learned solution is small in norm: the L1 error is 0.0163, the L2 error is 0.0193 and the error is 0.2705, which also includes the projection errors (difference in grid sizes). The horizontal axis is space and the vertical axis is time. (Online version in colour.)
Example 3.3 (Swift–Hohenberg equation) —
The Swift–Hohenberg equation is a scalar evolution equation with fourth-order derivatives
with x∈[0,50π]2. It is a model for thermal convection and solutions form various patterns depending on the choice of α and β. In this example, we will consider three parameter regimes where different patterns form: (α,β)=(0.1,0), which yield curves; (α,β)=(0.5,0), which yields a coral-like structure; and (α,β)=(0.05,0.5), which yields a hexagonal structure. For clarity, the Swift–Hohenberg equation can be written term by term as
These basic terms are used as some of the features in the learning method.
The input data for each column of table 3 use (α,β)=(0.1,0), (0.5,0) and (0.05,0.5) (respectively) and were simulated up to T=500, 5 and 15 (respectively). The noise levels are equal to 15.0%, 8.3% and 7.9% (respectively) and the learning parameter λ equals 0.5, 25 and 1 (respectively). The terms are all identified correctly and the coefficients are within 2.8% of the true value. This example shows that, although the feature space contains redundancies (because Δu=uxx+uyy), the method is able to find the underlying dynamics.
Table 3.
Example 3.3: Swift–Hohenberg. The true coefficients for each column are (α,β)=(0.1,0), (0.5,0) and (0.05,0.5) (respectively). The terms are all identified correctly and the coefficients are within 2.8% of the true value. This example shows that, although the feature space contains redundancies (because Δu=uxx+uyy), the method is able to find the underlying dynamics.
| terms | curves, noise=15.0% | coral, noise=8.3% | hexagonal, noise=7.9% |
|---|---|---|---|
| u | −0.8999 | −0.5001 | −0.9500 |
| u2 | 0 | 0 | 0.4999 |
| u3 | −0.9717 | −0.9751 | −0.9797 |
| u4 | 0 | 0 | 0 |
| ux | 0 | 0 | 0 |
| uy | 0 | 0 | 0 |
| 0 | 0 | 0 | |
| 0 | 0 | 0 | |
| uyux | 0 | 0 | 0 |
| uxx | 0 | 0 | 0 |
| uyy | 0 | 0 | 0 |
| uxy | 0 | 0 | 0 |
| Δu | −1.9842 | −1.9832 | −1.9843 |
| Δ2u | −0.9843 | −0.9838 | −0.9844 |
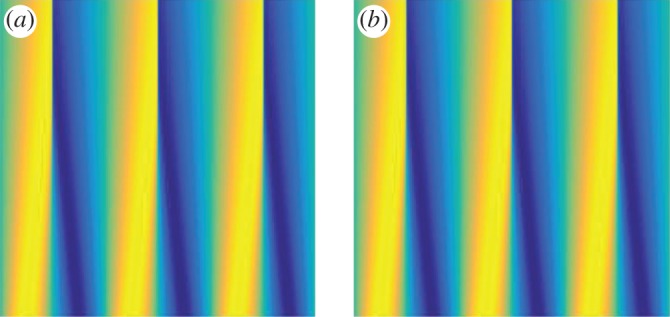
Figure 6a shows the original dynamics on a 65 536 point grid and figure 6b uses the coefficients from table 3 to simulate the data on a 16 384 point grid. The solutions are generated using a backward Euler step on the linear terms and a forward Euler step on the nonlinear terms. The solutions are plotted at T=250, 100 and 150, respectively. The learned solutions are qualitatively very similar to the original ones, thereby demonstrating the proposed method's ability to identify the correct parameter regimes for the various patterns. This could have applications to bifurcation and structure predictions.
Figure 6.
Example 3.3: Swift–Hohenberg. (a) The original dynamics on a 65 536 point grid and (b) the coefficients from table 3 used to simulate the data on a 16 384 point grid. The solutions are plotted at T=250, 100 and 150, respectively. (Online version in colour.)
Example 3.4 (Cahn–Hilliard equation) —
The Cahn–Hilliard equation,
with x∈[0,50π]2, is a model for phase separation in fluids. In this example, we will assume that the model takes the form: ut=ΔF(u), and use this as our ansatz to construct a feature space. In order to validate the proposed method's robustness to the size of the data used in the learning, we will vary the number of time stamps inputted in the algorithm.
The data are simulated up to T=2 using the Crank–Nicolson method with γ=0.5. In table 4, the terms are all identified correctly and the coefficients are within 1% of the true value. Similar to example 3.3, the learning is stable with respect to redundancies in the feature space. The input data to the learning method use uniform time steps with a total of 385, 85 and 25 time stamps. In all cases, the noise level is kept at 5.0%. The learned coefficients displayed in table 4 show that the method is robust to the number of time stamps used in the learning process.
Figure 7a shows the original data at T=20 and figure 7b uses the coefficients from column 3 of table 4 to simulate the data on 65 536 grid points. The solutions are generated using the Crank–Nicolson method. The learned solution, which uses the coefficients learned from 25 time stamps, is close to the original data: the L1 error is 0.0058 and the L2 error is 0.0329. Therefore, this suggests that the proposed method is robust to the size of the data.
Table 4.
Example 3.4: Cahn–Hilliard. The noise level is fixed at 5.0% for all three columns. The coefficients are within 1% of the true value. By varying the number of time steps retained in the simulation and inputted into the learning algorithm, we see that the method seems robust to the size of the data.
| terms | coefficients, 385 time steps | 85 time steps | 25 time steps |
|---|---|---|---|
| Δu | −0.9963 | −0.9936 | −0.9964 |
| Δ(u2) | 0 | 0 | 0 |
| Δ(u3) | 0.9952 | 0.9911 | 0.9927 |
| Δ(u4) | 0 | 0 | 0 |
| Δux | 0 | 0 | 0 |
| Δuy | 0 | 0 | 0 |
| Δuxx | 0 | 0 | 0 |
| Δuyy | 0 | 0 | 0 |
| Δuxy | 0 | 0 | 0 |
| Δ2u | −0.0996 | −0.0992 | −0.0994 |
| Δ2uxx | 0 | 0 | 0 |
| Δ2uxy | 0 | 0 | 0 |
| Δ2uyy | 0 | 0 | 0 |
| Δ3u | 0 | 0 | 0 |
Figure 7.

Example 3.4: Cahn–Hilliard equation. Plot (a) is the original data at T=20 and (b) uses the coefficients from column 3 of table 4 to simulate the data on 65 536 grid points. The learned solution, which uses the coefficients learned from 25 time stamps, is close to the original data. (Online version in colour.)
Example 3.5 (Navier–Stokes, low Reynolds number) —
The vorticity formulation for the two-dimensional Navier–Stokes equation is
Using this equation, the vorticity is simulated with x∈[0,2π]2 and is computed up to T=0.25 using the Crank–Nicolson method with various Reynolds numbers (Re>0). We will first consider the low Reynolds number case. Using Re=4 and Re=100, the learned coefficients can be found in columns 2 and 3 of table 5. The terms are all identified correctly and the coefficients are within 1% of the true value. In these two cases, the solutions exhibit smooth flows. Similar to examples 3 and 4, the learning is stable with respect to redundancies in the feature space. In column 1 of table 5, the Reynolds number is chosen to be small enough so that the dynamics are dominated by viscous flow. The coefficients in column 1 of table 5 show that the method identifies the viscous flow model, which is the true dominant behaviour of the data.
Table 5.
Example 3.5: Navier–Stokes, low Reynolds number. Note that −Δv=u. In the first column, the Reynolds number is chosen to be small enough so that the dynamics are dominated by viscous flow. The coefficients in the first column show that the method identifies the viscous flow model, which is the true dominant behaviour of the data. The coefficients are within 1% of the true value.
| terms | , noise=56.0% | Re=4, noise=56.8% | Re=100, noise=60.4% |
|---|---|---|---|
| u | 0 | 0 | 0 |
| u2 | 0 | 0 | 0 |
| u3 | 0 | 0 | 0 |
| ux | 0 | 0 | 0 |
| uy | 0 | 0 | 0 |
| 0 | 0 | 0 | |
| 0 | 0 | 0 | |
| uyux | 0 | 0 | 0 |
| vxux | 0 | 0 | 0 |
| vyux | 0 | −1.0047 | −1.0004 |
| vxuy | 0 | 1.0057 | 1.0006 |
| vyuy | 0 | 0 | 0 |
| uxx | 0 | 0 | 0 |
| uyy | 0 | 0 | 0 |
| uxy | 0 | 0 | 0 |
| Δu | 10.0563 | 0.2513 | 0.0101 |
| Δ2u | 0 | 0 | 0 |
Example 3.6 (Navier–Stokes, high Reynolds number) —
Using the vorticity formulation, we examine the turbulent flow case (i.e. Re≫1). The data are simulated using 1 048 576 grid points with Re=500 (very high Reynolds number relative to the coarse grid) and Re=1024 (vanishing viscosity on the coarse grid). It is known that the limiting flow (as the Reynolds number goes to infinity) of the Navier–Stokes flow on the torus is Euler's equation
Thus, one can argue that the underlying dynamics are truly governed by Euler's equation. In table 6, the learning is done using 65 536 grid points. The method identifies the correct terms (with respect to Euler's equation) and the coefficients are within 1% of the true value. The method picks out the coefficients to the intrinsic dynamics and not the equations used to simulate the data.
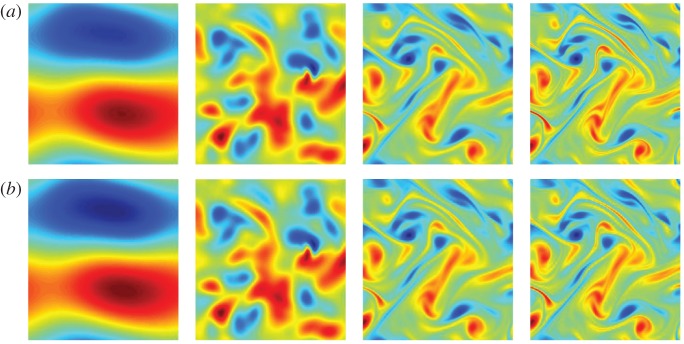
Figure 8a shows the original simulation using 1 048 576 grid points and figure 8b is the learned solution using the coefficients from tables 5 and 6 on a 65 536 point grid. From left to right the columns use: , Re=4, Re=100 and Re=1024. The results of figure 8 show that the learned PDEs yield qualitatively similar solutions.
Table 6.
Example 3.6: Navier–Stokes, high Reynolds number. The simulations are done on a 1 048 576 point grid and the learning is performed using 65 536 grid points.The method identifies the correct terms (with respect to Euler's equation) and the coefficients are within 1% of the true value. The method picks out the coefficients to the intrinsic dynamics and not the equations used to simulate the data. Note that −Δv=u.
| terms | Re=500, noise=15.3% | Re=1024, noise 14.9% |
|---|---|---|
| u | 0 | 0 |
| u2 | 0 | 0 |
| u3 | 0 | 0 |
| ux | 0 | 0 |
| uy | 0 | 0 |
| 0 | 0 | |
| 0 | 0 | |
| uyux | 0 | 0 |
| vxux | 0 | 0 |
| vyux | −0.9945 | −0.9931 |
| vxuy | 0.9976 | 0.9928 |
| vyuy | 0 | 0 |
| uxx | 0 | 0 |
| uyy | 0 | 0 |
| uxy | 0 | 0 |
| Δu | 0 | 0 |
| Δ2u | 0 | 0 |
Figure 8.
Example 3.6 Navier–Stokes, high Reynolds number. (a) shows the original simulation using 1 048 576 grid points and (b) uses the coefficients from tables 5 and 6 to compute the solution with 65 536 grid points. From left to right the columns use: , Re=4, Re=100 and Re=1024. (Online version in colour.)
Example 3.7 (homogenization of convection equation) —
One possible application of this method is the homogenization of highly oscillatory or random dynamics. As an example, consider the convection equation with oscillatory velocity
with initial data u0(x,x/ϵ) and x∈[0,2π]. The velocity field is assumed to be periodic and divergence free, i.e. div(a)=0. This is a linear model related to the homogenization of the incompressible Euler equation. Assuming sufficient smoothness, as , the solution homogenizes: , where u solves , with initial data , where is the average of v over the domain (see [37]).
For this example, the oscillatory velocity field is defined as
and the data are in t∈[0,0.25]. In table 7, the data are simulated using 1 048 576 grid points with and . The larger value of ϵ yields an oscillatory solution while the smaller value is closer (numerically) to the homogenized dynamics (see figure 9a,b). Step 4 of the method (the de-biasing step) is not used because the restriction of the normal equations to the identified terms is not well conditioned. The learning is done using 65 536 grid points. In the first column of table 7, the method identifies the correct terms but does not approximate the correct values of the coefficients because the velocity field is far from uniform and the approximation with this feature space is insufficient. In the second column of table 7, the method identifies the correct terms and approximates the coefficients to within 0.005% in relative error. Even though the data are not completely homogenized and no de-biasing is used, the method can approximate the underlying uniform dynamics.
Table 7.
Example 3.7: homogenization of the convection equation. The data are simulated using 1 048 576 grid points with and . Step 4 of the method (the de-biasing step) is not used because the restriction of the normal equations to theidentified terms is not well conditioned. The learning is done using 65 536 grid points. In the first column, the method identifies the correct terms but does not approximate the correct values of the coefficients because the solution is far from homogenized. In the second column, the method is within 0.005% of the true coefficients. No de-biasing is used because the restriction of the matrix onto the support set is ill conditioned.
| terms | , noise=9.5% | , noise=9.4% |
|---|---|---|
| u | 0 | 0 |
| u2 | 0 | 0 |
| u3 | 0 | 0 |
| ux | −1.3166 | −1.0000 |
| uy | 1.3537 | 1.9999 |
| 0 | 0 | |
| 0 | 0 | |
| uyux | 0 | 0 |
| uxx | 0 | 0 |
| uyy | 0 | 0 |
| uxy | 0 | 0 |
| Δu | 0 | 0 |
| Δ2u | 0 | 0 |
Figure 9.
Example 3.7: homogenization of the convection equation. (a,b) are the simulations computed using 1 048 576 grid points with (a) and (b). The larger value of ϵ yields an oscillatory solution while the smaller value is closer (numerically) to the homogenized dynamics. (c) is the learned solution using 65 536 grid points. (Online version in colour.)
Example 3.8 (travelling waves, solitons and ambiguity) —
As the coefficients and governing equations are learned from data, there is the potential for ambiguity when different equations generate similar datasets. For example, consider the Korteweg–de Vries (KdV) equation
3.1 on x∈[0,1] with initial data , whose solution is given by
3.2 Equation (3.2) is also a solution of the one-way wave equation
3.3 which leads to a potential issue with the recovery of the governing equation. As the one-way wave equation has fewer terms (a sparser governing equation), we expect the method to choose equation (3.3) over equation (3.2).
In table S1 in the electronic supplementary material, the data are simulated by equation (3.1) over t∈[0,0.1] using 512 grid points. In the first column of table S1 in the electronic supplementary material, we see that the method selects the one-way wave equation as the learned governing equation. This is indeed the sparsest governing equation (because it only uses one term in the model). In the second column of table S1 in the electronic supplementary material, ux is removed as a potential feature and the method is applied to the remaining terms. This results in the correct identification of the (intended) governing equation. This example shows that, when the dynamics governing the data can be represented by multiple equations, the method may not select the intended equation. However, the method will select a valid model equation (in this case the one-way wave equation). Model ambiguity is a potential issue with this approach when a large feature space is used.
Example 3.9 (additive noise on the data) —
In examples 3.1–3.8, the noise is assumed to be sampled from a Gaussian distribution and added directly to the velocity estimate. The underlying assumption is that the velocity is more severely corrupted by noise than the given data. In this example, Gaussian noise is added directly to the data themselves. As the data themselves are noisy, direct velocity estimation using finite differences is unstable.
Consider repeating example 3.1, where the data are simulated using
with , t∈[0,0.05] and x∈[0,1]. The data are corrupted directly and the velocity is calculated from the noisy data. Applying the method to this test case shows a recovery transition: the method produces accurate results before noise ≈3% and inaccurate results after ≈3% (the noise level is computed in the same way as before). This is due to an inaccurate approximation to the temporal and spatial derivatives. Data smoothing (or denoising) is probably needed to produce an accurate approximation. One possible smoothing approach is as follows: given noisy data un, a smooth approximation us is constructed by with a smoothing parameter β>0. The solution is given by us=(I−βΔ)−1un and is particularly simple to implement in the spectral domain (see [24] for more on spectral filtering). The learning algorithm is then applied to the filtered data us.
In table S2 in the electronic supplementary material, data from example 3.1 are corrupted by various noise levels and smoothed using β=5×10−5. When the noise level between the smoothed velocity and the velocity calculated from the noisy data is about 50%, the learned model is accurate (see the first column of table S2 in the electronic supplementary material). In figure S1 in the electronic supplementary material, a visual comparison between the estimated velocities is provided. Note that spectral filtering preserves the general spatial structure but may still contain some noisy frequencies. When the noise level between the smoothed velocity and the velocity calculated from the noisy data is large, the learned model loses accuracy and introduces false terms to compensate for the noise (see the second column of table S2 in the electronic supplementary material). This shows a potential issue with this approach when applied directly to noisy data. In particular, as derivatives must be calculated, instabilities are likely to form. Smoothing approaches using other regularizers, such as the total variation semi-norm, could be used to better approximate the derivative of noisy data (see [38]).
4. Conclusion
Sparse regression and other machine learning methods can provide scientists with important techniques to support their path to scientific discovery. This work presented one approach along this direction, in particular the use of L1 regularized least-squares minimization to select the correct features that learn the governing PDE. The identification of the terms in the PDE and the approximation of the coefficients come directly from the data. The numerical experiments show that the proposed method is robust to data noise and size, is able to capture the true features of the data, and is capable of performing additional tasks such as extrapolation, prediction and (simple) homogenization.
Supplementary Material
Acknowledgements
The author would like to thank the anonymous referees and the editors for their helpful comments on this manuscript.
Competing interests
I declare I have no competing interests.
Funding
H.S. was supported by NSF 1303892.
References
- 1.Bongard J, Lipson H. 2007. Automated reverse engineering of nonlinear dynamical systems. Proc. Natl Acad. Sci. USA 104, 9943–9948. (doi:10.1073/pnas.0609476104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Schmidt M, Lipson H. 2009. Distilling free-form natural laws from experimental data. Science 324, 81–85. (doi:10.1126/science.1165893) [DOI] [PubMed] [Google Scholar]
- 3.Brunton SL, Proctor JL, Kutz JN. 2016. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl Acad. Sci. USA 113, 3932–3937. (doi:10.1073/pnas.1517384113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tibshirani R. 1996. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 58, 267–288. [Google Scholar]
- 5.Candes E, Romberg J. 2007. Sparsity and incoherence in compressive sampling. Inverse Problems 23, 969–985. (doi:10.1088/0266-5611/23/3/008) [Google Scholar]
- 6.Baraniuk R. 2007. Compressive sensing. IEEE Signal Process. Mag. 24, 118–121. (doi:10.1109/MSP.2007.4286571) [Google Scholar]
- 7.Candes EJ, Romberg JK, Tao T. 2006. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 59, 1207–1223. (doi:10.1002/cpa.20124) [Google Scholar]
- 8.Elad M, Aharon M. 2006. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 15, 3736–3745. (doi:10.1109/TIP.2006.881969) [DOI] [PubMed] [Google Scholar]
- 9.Mairal J, Bach F, Ponce J, Sapiro G. 2009. Online dictionary learning for sparse coding. In Proc. 26th Annu. Int. Conf. on Machine Learning, Montreal, Canada, 14–18 June 2009 (eds L Bottou, M Littman), pp. 689–696. New York, NY: ACM.
- 10.Schaeffer H, Caflisch R, Hauck CD, Osher S. 2013. Sparse dynamics for partial differential equations. Proc. Natl Acad. Sci. USA 110, 6634–6639. (doi:10.1073/pnas.1302752110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mackey A, Schaeffer H, Osher S. 2014. On the compressive spectral method. Multiscale Model. Simul. 12, 1800–1827. (doi:10.1137/140965909) [Google Scholar]
- 12.Hou TY, Li Q, Schaeffer H. 2015. Sparse+ low-energy decomposition for viscous conservation laws. J. Comput. Phys. 288, 150–166. (doi:10.1016/j.jcp.2015.02.019) [Google Scholar]
- 13.Tran G, Schaeffer H, Feldman WM, Osher SJ. 2015. An L1 penalty method for general obstacle problems. SIAM J. Appl. Math. 75, 1424–1444. (doi:10.1137/140963303) [Google Scholar]
- 14.Nelson LJ, Hart GLW, Zhou F, Ozoliņš V. 2013. Compressive sensing as a paradigm for building physics models. Phys. Rev. B 87, 035125 (doi:10.1103/PhysRevB.87.035125) [Google Scholar]
- 15.Ozoliņš V, Lai R, Caflisch R, Osher S. 2013. Compressed modes for variational problems in mathematics and physics. Proc. Natl Acad. Sci. USA 110, 18 368–18 373. (doi:10.1073/pnas.1318679110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ozolinš V, Lai R, Caflisch R, Osher S. 2013. Compressed plane waves—compactly supported multiresolution basis for the Laplace operator. Proc. Natl Acad. Sci. USA 111, 1691–1696. (doi:10.1073/pnas.1323260111) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bright I, Lin G, Kutz JN. 2013. Compressive sensing based machine learning strategy for characterizing the flow around a cylinder with limited pressure measurements. Phys. Fluids 25, 127102 (doi:10.1063/1.4836815) [Google Scholar]
- 18.Alla A, Kutz JN.2016. Nonlinear model order reduction via dynamic mode decomposition. (http://arxiv.org/abs/1602.05080. )
- 19.Brunton SL, Tu JH, Bright I, Kutz JN. 2014. Compressive sensing and low-rank libraries for classification of bifurcation regimes in nonlinear dynamical systems. SIAM J. Appl. Dyn. Syst. 13, 1716–1732. (doi:10.1137/130949282) [Google Scholar]
- 20.Sargsyan S, Brunton SL, Kutz JN. 2015. Nonlinear model reduction for dynamical systems using sparse sensor locations from learned libraries. Phys. Rev. E 92, 033304 (doi:10.1103/PhysRevE.92.033304) [DOI] [PubMed] [Google Scholar]
- 21.Caflisch RE, Osher SJ, Schaeffer H, Tran G. 2015. PDEs with compressed solutions. Commun. Math. Sci. 13, 2155–2176. (doi:10.4310/CMS.2015.v13.n8.a8) [Google Scholar]
- 22.Brezis H. 1973. Operateurs maximaux monotones et semi-groupes de contractions dans les espaces de Hilbert, vol. 5 Amsterdam, The Netherlands: Elsevier. [Google Scholar]
- 23.Brezis H. 1974. Monotone operators, nonlinear semigroups and applications. In Proc. of the Int. Congress of Mathematicians, Vancouver, BC, 21–29 August 1974, vol. 2. See http://www.mathunion.org/ICM/ICM1974.2/ICM1974.2.ocr.pdf.
- 24.Hesthaven JS, Gottlieb S, Gottlieb D. 2007. Spectral methods for time-dependent problems, vol. 21 Cambridge, UK: Cambridge University Press. [Google Scholar]
- 25.Boyd S, Vandenberghe L. 2004. Convex optimization. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 26.Beck A, Teboulle M. 2009. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2, 183–202. (doi:10.1137/080716542) [Google Scholar]
- 27.Chambolle A, Pock T. 2011. A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40, 120–145. (doi:10.1007/s10851-010-0251-1) [Google Scholar]
- 28.Goldstein T, Osher S. 2009. The split Bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2, 323–343. (doi:10.1137/080725891) [Google Scholar]
- 29.Nesterov Y. 2004. Introductory lectures on convex optimization: a basic course, vol. 87 Berlin, Germany: Springer. [Google Scholar]
- 30.Nesterov Y. 1983. A method of solving a convex programming problem with convergence rate O(1/k2). Soviet Mathematics Doklady 27, 372–376. [Google Scholar]
- 31.Lions P-L, Mercier B. 1979. Splitting algorithms for the sum of two nonlinear operators. SIAM J. Num. Anal. 16, 964–979. (doi:10.1137/0716071) [Google Scholar]
- 32.Combettes PL, Pesquet J-C. 2011. Proximal splitting methods in signal processing. In Fixed-point algorithms for inverse problems in science and engineering (eds HH Bauschke, RS Burachik, PL Combettes), pp. 185–212. New York, NY: Springer.
- 33.Donoho DL. 1995. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 41, 613–627. (doi:10.1109/18.382009) [Google Scholar]
- 34.Combettes PL, Pesquet J-C. 2007. A Douglas–Rachford splitting approach to nonsmooth convex variational signal recovery. IEEE J. Selected Topics Signal Process. 1, 564–574. (doi:10.1109/JSTSP.2007.910264) [Google Scholar]
- 35.He B, Yuan X. 2012. On the O(1/n) convergence rate of the Douglas-Rachford alternating direction method. SIAM J. Num. Anal. 50, 700–709. (doi:10.1137/110836936) [Google Scholar]
- 36.Meyer Y. 2001. Oscillating patterns in image processing and nonlinear evolution equations: the fifteenth Dean Jacqueline B. Lewis memorial lectures. University Lecture Series, vol. 22 Providence, RI: American Mathematical Society. [Google Scholar]
- 37.Hou TY, Xin X. 1992. Homogenization of linear transport equations with oscillatory vector fields. SIAM J. Appl. Math. 52, 34–45. (doi:10.1137/0152003) [Google Scholar]
- 38.Chartrand R. 2011. Numerical differentiation of noisy, nonsmooth data. ISRN Appl. Math. 2011, 164564 (doi:10.5402/2011/164564) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.