Automated Algorithm for Detection of Transient Adenosine Release

Abstract

Spontaneous adenosine release events have been discovered in the brain that last only a few seconds. The identification of these adenosine events from fast-scan cyclic voltammetry (FSCV) data is difficult due to the random nature of adenosine release. In this study, we develop an algorithm that automatically identifies and characterizes adenosine transient features, including event time, concentration, and duration. Automating the data analysis reduces analysis time from 10–18 hours to about 40 minutes per experiment. The algorithm identifies adenosine based on its two oxidation peaks, the time delay between them, and their current vs. time peak ratios. In order to validate the program, 4 data sets from 3 independent researchers were analyzed by the algorithm and then compared to manual identification by an analyst. The algorithm resulted in 10 ± 4% false negatives and 9 ± 3% false positives. The specificity of the algorithm was verified by comparing calibration data for adenosine triphosphate (ATP), histamine, hydrogen peroxide, and pH changes and these analytes were not identified as adenosine. Stimulated histamine release in vivo was also not identified as adenosine. The code is modular in design and could be easily adjusted to detect features of spontaneous dopamine or other neurochemical transients in FSCV data.

Graphical abstract

Introduction

Adenosine is a byproduct of ATP catabolism and an important biological nucleoside involved in cell signaling,¹ neuromodulation,^1,2 and neuroprotection.^1,2 In the brain, adenosine regulates cerebral blood flow and modulates neurotransmission.^3,4 The ability to measure adenosine is important in understanding the roles it plays in neuromodulation and homeostatic regulation. Recently, direct measurements of spontaneous transient adenosine release in vivo have been made by fast-scan cyclic voltammetry (FSCV).⁵ These events are spontaneous, rather than stimulated, and last only a few seconds. Several hundred transients can occur in the 4 hour data collection typical of an in vivo experiment. Current data analysis protocols require a human analyst to pick the transients by hand; an experienced analyst can identify a transient approximately every 1.5 minutes. Therefore, if a data set contains 700 transients, then it would take about 18 hours to analyze. Adenosine transient events are random and do not follow any regular pattern so all the data must be painstakingly analyzed. In addition to being slow, identification by an analyst could be potentially inconsistent. Automating identification of adenosine transients would save time and normalize data analysis between researchers.

Algorithms have been developed to automate identification of molecules in chemical data.^6–16 For in vivo electrochemical data, peak identification has used the cyclic voltammogram (CV) as a chemical fingerprint to identify which peak is detected. However, there are 144,000 CVs collected in a four hour voltammetry experiment so they cannot be individually examined. Principal component regression (PCR) uses those cyclic voltammograms to identify compounds in a mixture and remove noise from the data.^17,18 In particular, PCR has proven to be a powerful tool to separate dopamine from pH shifts. This method was used previously to identify adenosine and create concentration vs time traces that are examined by an analyst to identify adenosine transients.³ The problem with PCR for adenosine is that the cyclic voltammogram of adenosine changes over time, with a primary peak that is large in the first few cyclic voltammograms and a secondary peak that grows in over time.⁵ Thus, it is hard to select a representative training set, the residuals (i.e. noise) are large, and the residual noise (Q) is often above the threshold residual noise (Q_α), denoting the training set is not sufficient to predict the concentration of the neurochemical.¹⁷ The other major problem for finding adenosine transients is that they are random events, with no unique time markers. While many dopamine events are linked to behaviors or cues, finding adenosine transients requires an algorithm that does not use time as a rule for identification.

In this study, an algorithm was designed to identify and characterize random adenosine transients from FSCV data. Our program automatically reads, analyzes, and creates a report characterizing the duration, concentration, and event time for each adenosine transient. This automated analysis takes only about 40 minutes to analyze a four hour in vivo data set. The program was validated with 4 data sets from 3 independent researchers and compared to the results of the analysts. The program resulted in 10 ± 4% false negatives (FN), due to multiple peaks and high thresholds, and 9 ± 3% false positives (FP), due to random noise that occurs in biological experiments. The algorithm was tested against ATP, histamine, hydrogen peroxide, and pH, known interferents in the brain, and only generated one false positive in 82 measurements. This study demonstrates the reliability of the automated identification program for adenosine and the program is customizable to study other electroactive analytes in the future. Automated analysis of FSCV data will allow faster data analysis and less analyst bias for identifying and characterizing adenosine in vivo.

Results and discussion

Rules for adenosine detection

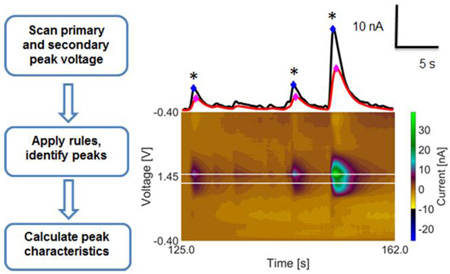
In order to develop an automated program to detect adenosine transients, rules must be constructed about what constitutes a transient. In a typical fast-scan cyclic voltammetry experiment, the voltage is ramped up and back to collect a cyclic voltammogram (CV) and the scan is repeated every 100 ms. Large background currents due to capacitive charging are subtracted out to reveal Faradaic current changes over time. Because of the large amount of data, multiple CVs are often viewed as a three dimensional color plot, with data stacked horizontally as a function of time. The color plot in Fig. 1 shows spontaneous adenosine transients in vivo. Adenosine is irreversibly oxidized around 1.4 V and forms a primary product,¹⁹ which can be oxidized again to form a secondary product.⁴ The oxidation of this secondary product is detected on subsequent scans at 1.0 V. The presence of two oxidation peaks for adenosine within the CV is a hallmark of its detection and the voltage at which these peaks occur is constant for an experiment.

Figure 1.

In vivo spontaneous adenosine transients in the hippocampus. Top: CVs of adenosine are taken from a single adenosine transient event, showing changes of adenosine over time. CV 1 is when adenosine first appears. CV 2 is when the primary peak is at a maximum and CV 3 is when the secondary peak is at maximum. Middle: Current vs. time traces with 5 transients detected. The primary peak maximums (black trace) occur before secondary peak maximums (red trace) and is the basis for the lag time filter (diamonds mark peak max values). The S_p / P_p ratios for each of the 5 peaks are between 0.49 and 0.89. Bottom: False color plot of adenosine transients with white lines marking the primary and secondary oxidation voltages.

Taking the current at the primary and secondary peak voltages from the CV and plotting it vs. time reveals how adenosine changes over time (above color plot, Fig. 1). In this current vs time trace, the peak current maximums are marked as diamonds and the primary peak always occurs before the secondary peak because the primary product is the precursor for the secondary product.²⁰ In addition, the primary transient peak current is larger than the secondary peak current because not all of the primary product is oxidized to secondary product on the subsequent scan. CVs of adenosine were taken from a single adenosine transient event to show the changes in adenosine CV over time. CV 1 shows the first appearance of adenosine with a primary peak and no secondary peak, CV 2 is taken at a maximum current of primary peak and the secondary peak is growing in, and CV 3 is taken at the maximum of the secondary peak. Analysis of 108 in vivo transients (from 3 rats) reveals this secondary to primary peak ratio is between 0.49 and 0.89 and this range was used to as a filter for identifying in vivo adenosine transients. The secondary peak redox reaction is reversible and the duration of this peak in the current vs time trace is longer than the duration of primary peak because the secondary product can be reformed and oxidized again on future scans. These data illustrate the rules for identifying an adenosine transient in current vs. time traces: (1) a peak must be present at both the primary and secondary oxidation voltages; (2) the secondary peak must lag the primary peak; (3) the ratio of secondary to primary peak currents must be in an acceptable range consistent with adenosine; (4) the duration of secondary peak must be longer than the primary peak in current vs. time traces. Additionally, the adenosine transients are fast, so the duration must be between 0.6 (smallest peak that can be empirically observed with our 0.1 s temporal resolution) and 15 s (over 5 s larger than empirically observed largest transient) and all peaks must have S/N ratios greater than 3. With these rules, an algorithm for adenosine transient identification was built.

Overview of adenosine algorithm

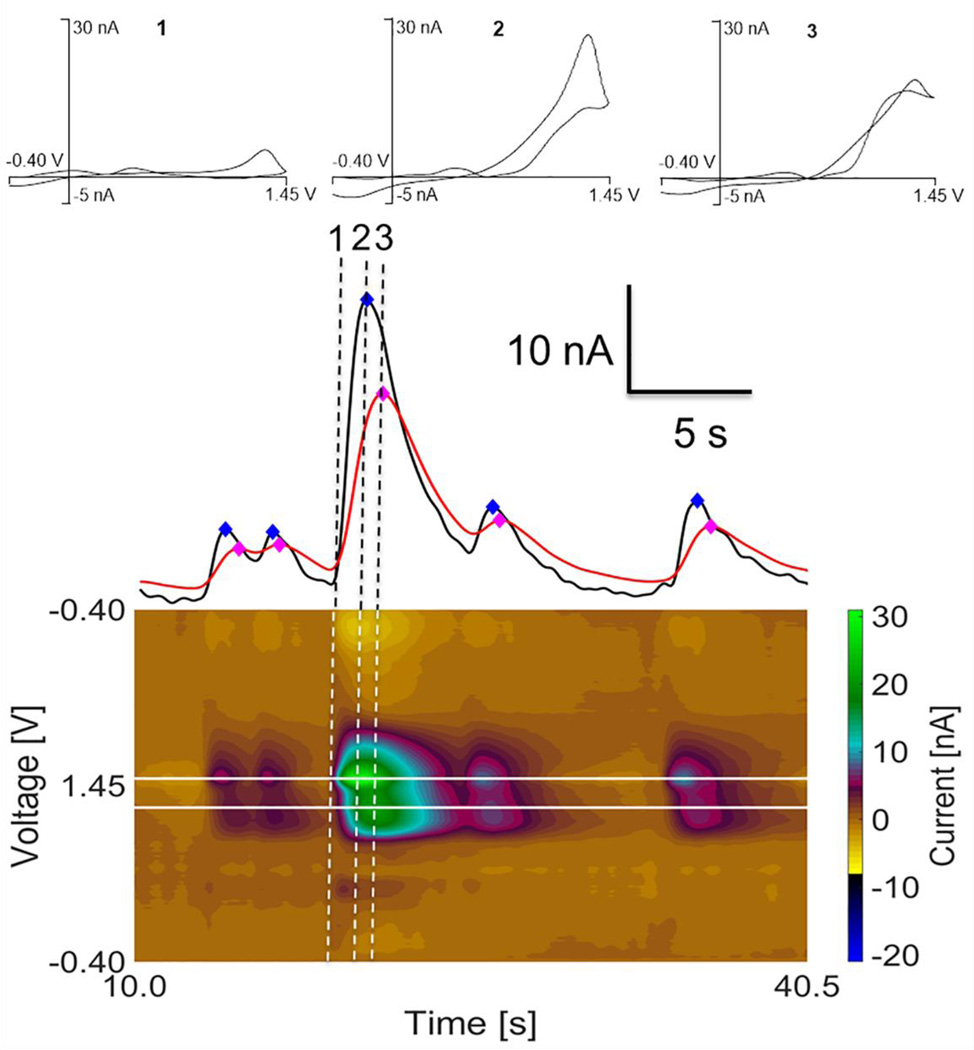
Fig. 2 shows a schematic overview of the automated algorithm for adenosine detection. Three dimensional raw data is read into the program and then background subtracted²¹ at defined intervals (incremental background subtraction). The primary and secondary maximums are scanned for peaks in current vs. time traces. In order to verify the peak is an adenosine transient, it is more accurate to background subtract directly adjacent to the peak. With this adjacent background subtraction, if a peak is detected that meets all rules for adenosine (S/N >3, secondary lags primary and is longer in duration, secondary to primary peak ratio in correct range) then the peak is counted as an adenosine transient. The program then automatically records the peak height, of the primary peak, using Matlab’s findpeaks.m function as well as the time at which the peak maximum occurs.

Figure 2.

Algorithm for FSCV transient. (1) Files are read into the program and background subtracted at defined increments. (2) Primary and secondary oxidation voltages are scanned for adenosine (ADO) peaks. (3) Lag time filter is applied to make sure two peaks are present and the secondary peak lags the primary peak (4) resultant peaks are background subtracted adjacent to the peak then (5) identified similarly to steps 2 and 3. (6) Signal-to-noise and ratio filter are applied to detected peaks to remove spurious peaks. (7) Event time, concentration, and duration are written to file.

Algorithm Inputs

The algorithm requires a few inputs by the analyst in order to search for adenosine transients. First, the voltages for the primary peak and secondary peaks, termed p_max and s_max respectively must be determined. Using the in vivo data, the peak voltages are chosen by reviewing a few large adenosine transients in the data set; voltages generally vary only slightly between electrodes. Second, the analyst must choose a peak current threshold, i.e. the minimum current for a peak in the current vs time trace. The minimum peak threshold can be chosen by determining the noise in a part of a trace and then picking three times the noise or one can be more lenient in the screening process, using a lower threshold, and then apply a more stringent S/N filter later. Generally, for in vivo data we used a minimum peak threshold around 2 nA, but for slice data, the noise is smaller and this value could be set closer to 1 nA. Third, the prominence is defined (Supplemental Figure 1). This value defines the minimum height, in current, of the valley between two overlapping peaks. In general, we empirically found that leaving this value at 0.64 nA is a good balance between identifying multiple peaks clustered together and rejecting noise. This means the smaller of the two overlapping peaks has a height from valley to peak that is greater than 0.64 nA. The minimum prominence value was used to filter out peak noise and therefore its value was kept constant. Fourth, the lag time filter is defined. For a peak to be identified as adenosine it must have a peak both at the primary and secondary voltages and the secondary peak must lag the primary peak by at least 0.1 s but be within 2.5 s of the primary peak. The 0.1 s is the minimum lag time possible given our temporal resolution of 0.1 s and the 2.5 s was larger than any empirically determined delay (n=108 peaks, 3 rats). Finally, the analyst inputs the expected ratio of secondary peak max current to primary peak max current for adenosine, S_p/P_p. This ratio was empirically determined to be 0.49 to 0.89 from an analysis in vivo transients, but could differ for different waveforms or types of electrodes.

Background Subtraction

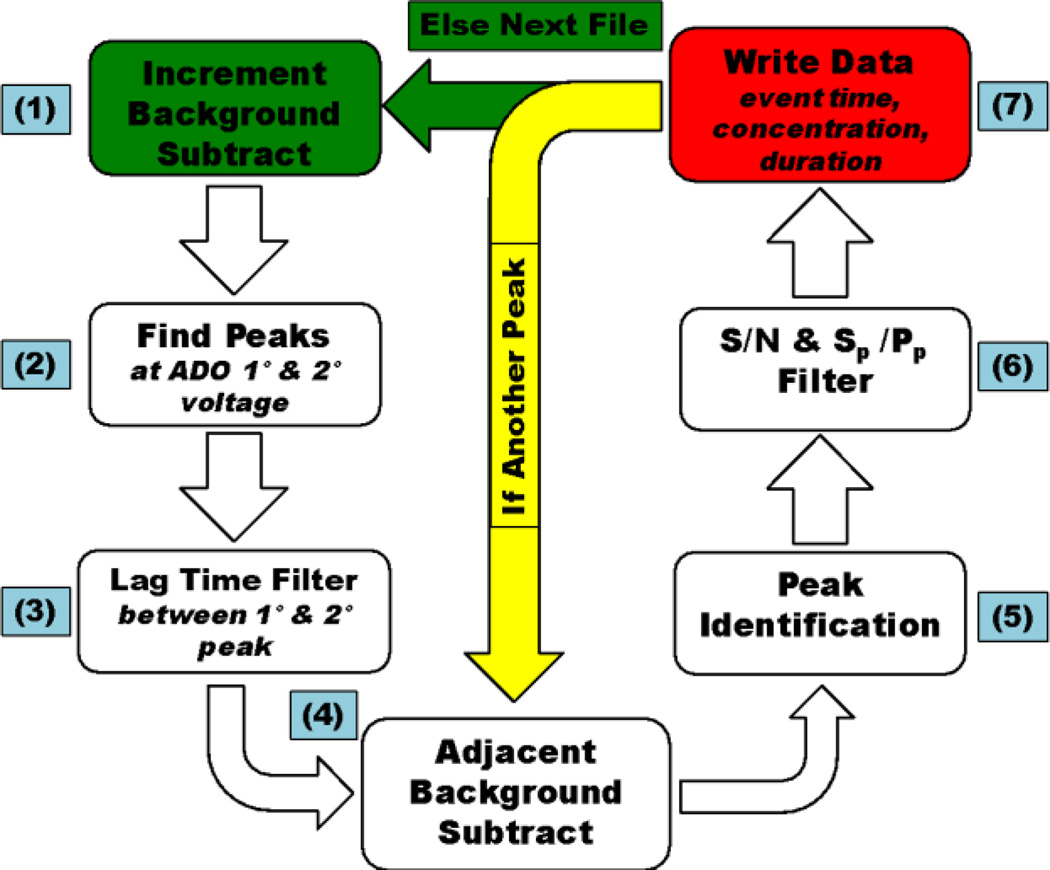
In FSCV experiments, stable non-faradaic currents occur due to background charging of the surface of the CFME and these background currents are subtracted to study Faradaic redox reactions. Because the locations of adenosine transients are not known a priori, it is not obvious where to pick to perform background subtraction. Thus, the program first picks several places for background subtraction, at defined increments, and then background subtracts each data set at these times. By examining the same data set background subtracted from different places, we correct for 2 fundamental problems. First, if we only picked one background subtraction time, it may inadvertently be during an adenosine peak and the results would not be interpretable. Second, the background current drifts over time so background subtraction should be performed as near to a peak as possible to accurately identify and define all possible adenosine peak characteristics. Figure 3 A–C shows color plots of the same data, background subtracted at 3 different time points. Long duration color changes, away from the oxidation peaks, are due to electrode drift and thus, it is easier to distinguish small transients from drift if the background is taken nearby. Practically, after the initial background subtraction, the program iterates at a defined increment value (usually 10s) repeating the procedure of doing a background subtraction and identifying adenosine transients using that background point. All potential adenosine transients are collected and identified by event time for use in the next step, adjacent background subtraction.

Figure 3.

Incremental background subtraction of in vivo adenosine transients from the hippocampus brain region. A.) Background subtraction at 50 s. B.) Background subtraction at 100 s. C) Background subtraction at 150 s. The white vertical lines show where the background was taken.

It is standard to do background subtraction directly adjacent to the peak,⁵ so the next part of the algorithm uses the event times for putative transients to background subtract adjacent to the peak. Adjacent background subtraction is performed approximately 2.5 s before each peak and results in a more accurate determination of concentration change and duration because there is less background drift. The time input for adjacent background subtraction is generated from the event times obtained during incremental background subtraction and 10 baseline data points are included for background subtraction. If spurious peaks are collected during the increment part of the algorithm, they are often rejected when adjacent background subtraction is performed. The incrementing part of the program is a wide net to collect all potential transients while during adjacent background subtraction, threshold values are set higher and therefore are more discriminating. Once peaks are found with adjacent background subtraction, they are subject to the lag time filter, S_p/P_p ratio filter and S/N filter that identifies them as adenosine transients. The program then calculates the peak height from the primary peak in current, which can be changed to concentration with a known calibration value, which has been previously described.⁵ In addition, the peak width at half height is calculated for each peak as well as the S/N value. Peaks that are identified in the initial incremental background stage but rejected in the more stringent adjacent background stage are flagged in the output for what criteria they fail (Fig. S2). Thus, an analyst could go back and check these peaks if desired.

Analyst validation of adenosine transient program

To determine the robustness of the adenosine transient program, the algorithm was tested by comparing transients identified by the program to data analyzed by an analyst using traditional methods. The analyst used principal component regression to produce a trace of adenosine concentration changes using High Definition Cyclic Voltammetry (HDCV), a program developed in the Wightman lab.²² Table 1 shows false positives and negatives for the algorithm compared to the analyst for 4 different data sets. If the algorithm selects a peak that was not identified as adenosine by the analyst, it is counted as a false positive (FP). If the analyst finds a peak that the program missed, it is counted as a false negative (FN). Each data set was from an independent animal experiment and data sets were obtained from three separate researchers. In the first data set (S1), an in vivo measurement in the caudate putamen, only 41 adenosine transients were observed and the FP and FN were below 5%. Data sets 2 and 3 were in vivo measurements in the hippocampus, with more adenosine transients and a slightly higher FN and FP rate. In data set S4, a brain slice experiment from the prefrontal cortex, the algorithm resulted in 16% FN and 7% FP. Overall, analyst validation of the adenosine algorithm resulted in 10 ± 4% FN and 9 ± 3% FP for a total of 640 confirmed adenosine transients.

Table 1.

Analyst validation of adenosine transient data sets. S1 is an in vivo measurement in the caudate putamen. S2 and S3 are in vivo measurements in the hippocampus. S4 is a brain slice experiment from the prefrontal cortex. Each data set is an independent experiment

	S1	S2	S3	S4	Total
False Negative	5%	10%	8%	16%	10 ± 4%
False Positive	2%	10%	9%	7%	9 ± 3%
n (transients)	41	397	112	90	640

The concentration of the transients and the event times of the transients were also compared between the analyst and the algorithm. For concentration, the average difference between the analyst and algorithm was 0.029 ± 0.002 µM (n=397 transients, 3 data sets) which was statistically different than the expected value of 0 (p<0.001). The algorithm consistently reported slightly lower concentrations than the analysts (by about 15%), likely due to the algorithm accounting for baseline changes near the peak. Alternatively, the difference could be that the analyst tends to maximize the current value by adjusting their background subtraction location, while the algorithm has set rules for background placement. While the peak concentrations were slightly lower with the algorithm, it was consistent in its definition and the concentrations are only estimates due to the calibration factors being obtained in vitro. For event time, the difference between the analyst and algorithm reported times was 0.008 ± 0.009 s, not significantly different than the expected value of 0 (p=0.45, n=397 transients, 3 rats). The event durations were not compared, because the analyst did not have a good method to determine the duration at half-height. Previously, we had reported peak durations as the full width of the peak⁵ so duration values here are shorter, but are in line with expected results.

Statistics were calculated for each data set (then averaged) and the adenosine algorithm had a mean precision of 0.91 ± 0.01, meaning that 91% of the peaks it returned were commonly identified peaks. The sensitivity of 0.90 ± 0.04 indicates that 90% of peaks identified by the analyst were also found by the program. The accuracy of 0.90 ± 0.02 is geometric mean of sensitivity and precision, weighting both FP and FN to determine the overall accuracy. Thus, the program is 90% accurate in identifying transients, showing it can discern adenosine, with a high degree of certainty in a similar manner as an analyst.

Neither the algorithm nor the human analyst is perfect at identifying adenosine transients. When checking the algorithm against the human, we found that the analyst was less likely to find transients in the beginning and end of the files, due to background subtraction issues and difficulty visualizing transients on the edges of the color plots. In addition, the analysts did not have a good way to calculate signal to noise in our traditional method, so an analyst may infrequently count a peak with an S/N less than 3. For the algorithm, false positives were mainly due to noise. False negatives were primarily due to multiple peak maximums occurring in a single peak (i.e. a human might count 3 peaks close together where the computer would find 1 or 2). However, it will always be difficult to measure the concentration and duration of multiple peaks that do not go back to baseline. The program can flag potential multiple peaks so that the analyst can go back to better examine that data. Ultimately, false positives and false negatives are minimized by setting thresholds properly in both background subtraction parts of the adenosine algorithm.

Testing biologically relevant interferents (in vitro)

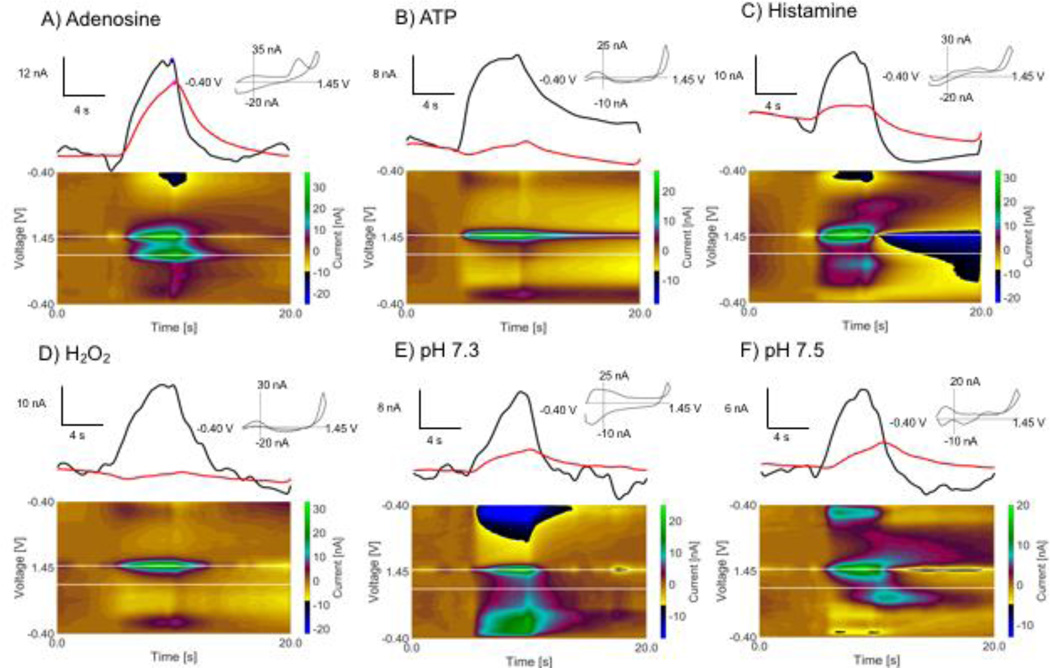
There are many electroactive molecules in the brain that have electrochemical signatures that are similar to adenosine. In order to test the robustness of the algorithm, adenosine and possible interferents were measured in vitro. P_max and S_max were determined for adenosine for an electrode and then data from possible interferents run through the algorithm to determine if it would be identified as adenosine. The ratio of secondary to primary peaks was critical for identifying interferents.

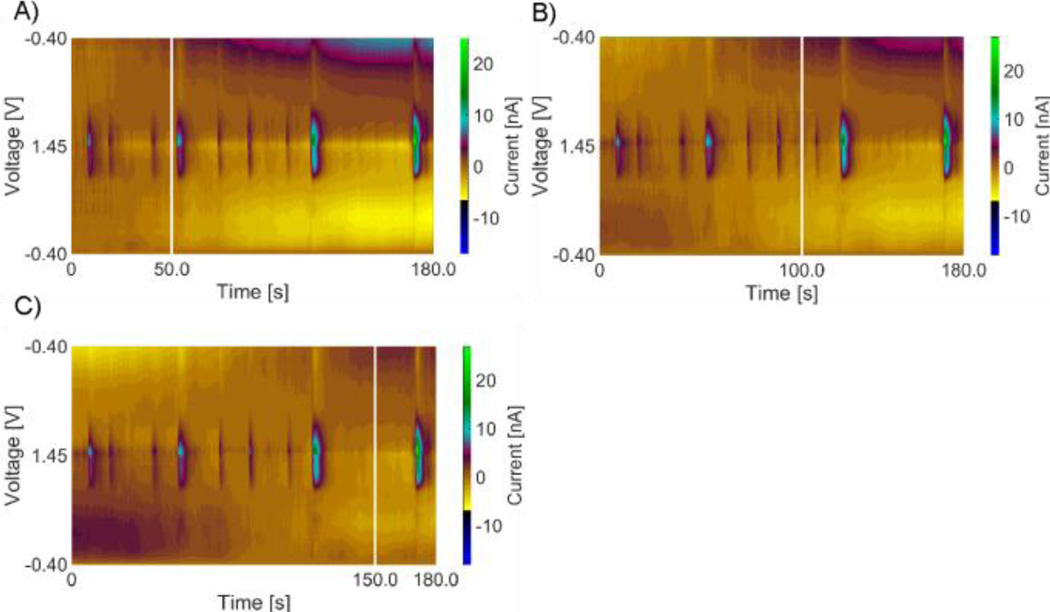
Fig. 4 shows example electrochemical data for adenosine as well as potential interferents adenosine triphosphate (ATP), histamine, hydrogen peroxide,²³ and pH. ATP differs from adenosine by only three phosphate groups and has the same electrochemical moiety.²⁰ ATP has primary and secondary peaks but the secondary peak is not as prominent, so the S_p/P_p ratio is below the threshold for adenosine (mean=0.18±0.05, range=0.07–0.27, 15 injections, 6 electrodes). In addition, the secondary maximum occurs before the primary maximum. Thus, ATP fails to be identified as adenosine. Histamine also has 2 oxidation peaks, but the secondary peak maximum is at 0.76 V instead of 1.06 V. Thus, when the program scans for a secondary peak at 1.06 V, the peak there is small and histamine fails for a S_p/P_p ratio below threshold (mean=0.15±0.07, range=0.03–0.24, 20 injections, 6 electrodes). Hydrogen peroxide does not have a prominent secondary peak. Although some current from the primary peak is present at 1.06 V, it fails for the S_p/P_p ratio of 0.18 (mean=0.08±0.05, range=0.03–0.18, 19 injections, 6 electrodes) and not having a time lag between the peaks. Finally, we tested pH changes of 0.1, both acidic and basic. The max S_p/P_p ratio for pH 7.3 and pH 7.5 are below threshold (pH 7.3, mean=0.19±0.09, range=0.06–0.30, 13 injections, 6 electrodes; pH 7.5, mean=0.20±0.09, range=0.07–0.37, 15 injections, 6 electrodes). The algorithm has a maximum duration of a transient for in vivo data and pH shifts are generally long lasting, so they would not be likely to generate false positives in vivo. These experiments show that biologically relevant interferents do not result as false positives for adenosine during in vitro calibration experiments and help solidify the identity of the species detected as adenosine.

Figure 4.

In vitro testing of biologically relevant interferents. Current vs timetraces, cyclic voltammograms, and false color plots for A) 1 µM adenosine, B) 1 µM ATP, C) 1 µM histamine, D) 1 µM hydrogen peroxide, E) pH 7.3 shift, F) pH 7.5 shift. Interferents are rejected by the algorithm due to s_max occurring before p_max and an interferent S_p,/P_p ratio below the minimum for adenosine.

Future studies could also examine mixtures of adenosine and interferents to determine the extent to which potential corelease of an interferent might obscure adenosine detection by the algorithm. Although principal component regression is useful for dopamine analysis to remove contributions from pH or noise,²⁴ it is more challenging for adenosine where the CVs are not consistent over time (Fig. 1). Here, chemical noise is not removed here but we rely on the filters to remove transients that do not fit the rules for adenosine. Another limitation is that the analyst defines the primary and secondary peak voltages because it could lead to potential bias; future work will focus on automatically determining these inputs. Other strategies, such as image analysis of color plots might be more useful for deconvoluting mixtures, but the overall conclusion here is that adenosine transients can be clearly detected and are not due to these other possible interferents.

In vivo testing of stimulated histamine

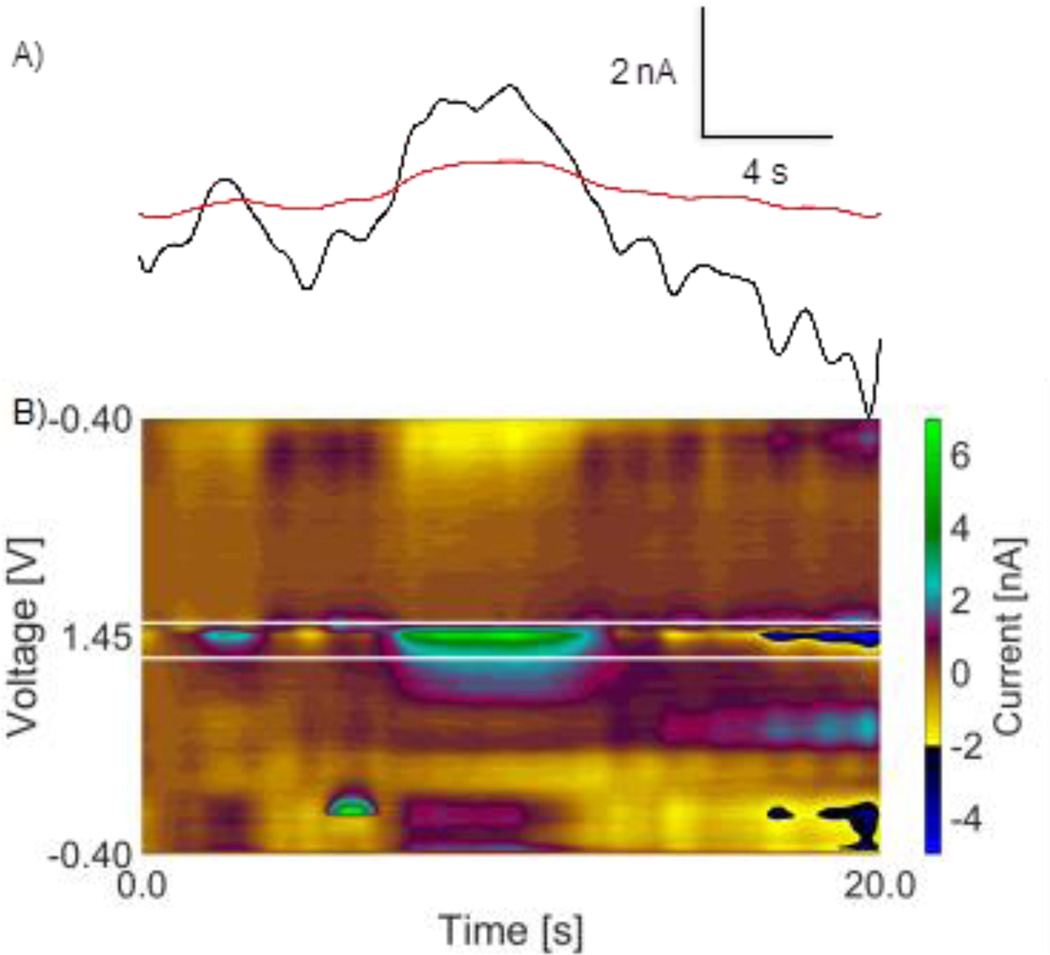
Redox voltages and currents observed during in vivo experiments can differ from those observed during in vitro experiments. Histamine is a possible interferent for adenosine due to similar cyclic voltammograms and a secondary peak formation.²⁵ While in vitro data showed that histamine would not be counted as an adenosine transient, to further validate this in vivo, we performed a stimulated histamine release experiment and ran the result through the adenosine algorithm. Measurements were made in the premammillary nucleus with a stimulating electrode in the medial forebrain bundle region. Figure 5 shows the results for the in vivo histamine stimulation.²⁵ The white lines are the peak max values for adenosine; both the primary and secondary peak maximums for histamine occur at a lower voltage than the adenosine peak maximums. Histamine fails to be identified as an adenosine transient because it fails both the lag time filter and the S_p/P_p ratio filter. Histamine also failed the lag time and peak ratio filters in vitro, showing that the calibration tests produced similar results to the in vivo test. Overall, this validation shows that the algorithm is good at distinguishing adenosine from histamine during both in vitro calibration experiments and in vivo.

Figure 5.

in vivo stimulated histamine from the premammillary nucleus. A) Primary (black) and secondary (red) oxidation peak i vs t traces of stimulated histamine fail lag time filter because maximums occur at the same time. B) False color plot of stimulated histamine. White lines are p_max and s_max generated from adenosine transients.

While we have optimized this algorithm for finding adenosine transients, the software is modular and could easily be trained with “new rules” to identify other analytes in FSCV data. For example, dopamine could be detected by setting the algorithm to scan the oxidation and reduction voltages for dopamine, having a lag-time of zero, and inputting an expected reduction to oxidation peak ratio range. Alternatively, dopamine data could be pre-processed by principle components regression to remove noise^26,24 and the program could then subsequently pick the peaks and characterize them from that trace. Another possible extension is to look for multiple analytes in the same data. Adenosine and oxygen release events are correlated,²⁷ so the program could scan the reduction voltage for oxygen and identify oxygen transients that occurs after an adenosine transient. Thus, as long as there is enough information to make rules about detection from the electrochemical data, this modular program can be used to automatically pick peaks and characterize them. Ultimately, this automated algorithm can save hundreds of hours of tedious data analysis and normalize data analysis between analysts.

Conclusions

An automated algorithm was built to identify transient changes in adenosine concentration in in vivo data sets. The algorithm uses rules about the electrochemistry of adenosine to identify peaks and is 90% accurate. Data from multiple analysts, brain regions, and types of tissue were analyzed and the algorithm was found to be robust. The algorithm detects adenosine but not possible interferents, both in vitro and in vivo and they did not cause false positives. This algorithm could be adjusted to detect many other electroactive compounds in neurochemistry experiments. In summary, an automated algorithm to identify adenosine peaks will be useful for streamlining and accelerating data analysis and will therefore increase laboratory throughput.

Methods

FSCV Transient

The adenosine feature detection algorithm, named FSCV Transient, was written in Matlab 2016a (The MathWorks Inc, Natick, MA, USA) and run on a 3.4 GHz PC computer with Windows 10 for data analysis. The user inputs are first defined: maximum primary (p_max) and secondary (s_max) oxidation voltage, background subtraction increment value, and threshold level for a peak for both background subtraction stages. There are also values such as prominence, S_p/P_p ratio, and peak duration that can be changed, but are usually left at a default value. Experimental data was collected using High Definition Cyclic Voltammetry (HDCV), a program developed in the Wightman lab.²² Non-background subtracted and non-filtered FSCV color plot data were exported from HDCV and imported into Matlab. Then the FSCV data is convoluted with a 2-D Gaussian filter (size=7, σ=2), which is a low-pass blurring filter that removes noise and a median filter [3×3] is applied to further smooth the data set.

In the first part of the algorithm (Figure 2, Steps 1–3), incremental background subtraction is performed by background subtracting at several times, then searching the primary and secondary peak traces for peaks. For example, an initial background subtraction occurs at t = 1.0 s, the two current vs. time traces are scanned for adenosine peaks, and every peak over threshold is compiled and concatenated until the end of file. Then the program would background subtract at the next defined increment value, usually 10 s, and search again for peaks. A typical increment value of 10.0 s would result in 17 incremented background subtractions in a 180 s file. After all possible adenosine peaks are amassed and duplicates are removed, the algorithm imposes a constraint that a peak must be detected at both the primary and secondary voltages and that the primary adenosine peak maximum must occur before the secondary peak maximum. The final set of event times identified during incremental background subtraction is subsequently used as seeds during the second part of the program, adjacent background subtraction.

In the second part of the algorithm (Steps 4–7), adjacent background subtraction is accomplished by performing background subtraction approximately 2.5 s before, i.e. adjacent to, each individual peak found during incremental background subtraction. Adjacent background subtraction is more accurate for measuring peak characteristics because of possible baseline drift. The minimum concentration that can be detected is usually around 40 nM. Additionally, the noise is calculated as the standard deviation of the baseline taken adjacent to the peak and only peaks with S/N > 3 are kept. Supplemental Fig. 2 shows the output from our program of peak current, duration, and event time, including peaks that are flagged as not meeting the criteria for being an adenosine peak.

Chemicals

The effect of interferents was tested in vitro using a flow-injection system.²⁸ Compounds were dissolved in PBS buffer containing (in mM) 131.25 NaCl, 3.0 KCL, 10.0 NaH₂PO₄, 1.2 MgCl₂, 2.0 Na₂SO₄, and 1.2 CaCl₂ (pH 7.4, all Fisher Scientific, Fair Lawn, NJ). All aqueous solutions were prepared with deionized water (Milli-Q Biocel; Millipore, Billerica, MA, USA). Adenosine, histamine, and adenosine triphosphate were purchased from Sigma Aldrich and hydrogen peroxide was purchased from Macron (Center Valley, PA, USA). All were made up as 10.0 mM stock solutions in 0.1 M HClO4 and then diluted to their concentration in PBS buffer. The interferent pH was tested by adjusting pH=7.4 PBS buffer to pH=7.3 with HCl or pH=7.5 with NaOH.

Carbon-fiber microelectrodes and FSCV

Carbon-fiber microelectrodes (CMFEs) were prepared with standard fabrication techniques using 7 µm diameter T-650 carbon fibers with a length between 100 – 150 µm (Cytec Engineering Materials, West Patterson, NJ, USA)²⁹. Data were collected using a Dagan ChemClamp potentiostat (Dagan Corporation; Minneapolis, MN, USA). All electrodes were scanned from a holding potential of −0.40 V and scanned to a switching potential of 1.45 V and back at 10 Hz versus a Ag/AgCl reference electrode, at a scan rate of 400 V/s.

Data sets analyzed

All animal experiments were approved by the University of Virginia Animal Care and Use Committee. In vivo data set (S1) was measured in the caudate putamen (coordinates: ML: +2.0, AP +1.2, DV −4.5) and data sets (S2 and S3) were measured in the hippocampus (coordinates: ML: +2.0, AP −3.8, DV −2.5) according to procedures previously described.⁵ The brain slice data was measured in the prefrontal cortex, as previously described.²³ Analysts chose adenosine transients using principal components analysis in HDCV, using the 5 largest transients as the training set, according to our established procedure.⁵ Peak heights and event times were hand calculated for each peak.

Error analysis

Sensitivity, precision, and accuracy were calculated from true positive (TP), false positive (FP), and false negative (FN) values determined from analyst validation of FSCV transient algorithm results. The analyst data was assumed to be the true data, since no true data exists. Sensitivity or recall is the fraction of relevant peaks that are returned by the algorithm from the data set. If the algorithm contains a large number of FNs the sensitivity decreases.

$$\mathit{\text{Sensitivity}}=\frac{TP}{TP+FN}$$ (1)

Precision or positive predictive value is the fraction of peaks returned by the algorithm from the data set that are relevant peaks. If the algorithm contains a large number of FPs the precision decreases.

$$\mathit{\text{Precision}}=\frac{TP}{TP+FP}$$ (2)

Accuracy was calculated from the F₁ score, which is the harmonic mean of sensitivity and precision. The harmonic mean weights sensitivity and precision equally.

$$\mathit{\text{accuracy}}=2\frac{\mathit{\text{sensitivity}}\times \mathit{\text{precision}}}{\mathit{\text{sensitivity}}+\mathit{\text{precision}}}$$ (3)

Data are presented as mean ± standard deviation.