Elasticity of the transition state for oligonucleotide hybridization

Abstract

Despite its fundamental importance in cellular processes and abundant use in biotechnology, we lack a detailed understanding of the kinetics of nucleic acid hybridization. In particular, the identity of the transition state, which determines the kinetics of the two-state reaction, remains poorly characterized. Here, we used optical tweezers with single-molecule fluorescence to observe directly the binding and unbinding of short oligonucleotides (7–12 nt) to a complementary strand held under constant force. Binding and unbinding rate constants measured across a wide range of forces (1.5–20 pN) deviate from the exponential force dependence expected from Bell's equation. Using a generalized force dependence model, we determined the elastic behavior of the transition state, which we find to be similar to that of the pure single-stranded state. Our results indicate that the transition state for hybridization is visited before the strands form any significant amount of native base pairs. Such a transition state supports a model in which the rate-limiting step of the hybridization reaction is the alignment of the two strands prior to base pairing.

INTRODUCTION

The hybridization or annealing of nucleic acids (NA), in which two complementary strands base pair to form a duplex, is one of the most fundamental processes in biology. It is prominent in a wide variety of cellular NA transactions such as nucleic acid polymerization during replication and transcription, strand invasion during homologous recombination, gene silencing by Argonaute proteins and sequence targeting by CRISPR systems, to name a few examples. In addition, scientists have exploited the hybridization of nucleic acids to develop molecular biology techniques such as polymerase chain reaction (PCR), fluorescence in situ hybridization and RNA interference, and more recently to construct NA-based nanostructures, nanomachines and nanosensors (1–6). Although the hybridization reaction has been under investigation for many years and a number of studies have yielded important thermodynamic and kinetic parameters (7–9), the determinants underlying these parameters remain poorly quantified. Recently, single-molecule techniques have been used to probe annealing and melting kinetics one molecule at a time, revealing behavior normally masked by ensemble averaging (10–12). Single-molecule force spectroscopy in particular has proven to be a powerful tool to study this process, as the application of force modulates the reaction rates (13–16) and can provide a well-defined coordinate for the reaction (17,18).

Here, we use a recently described optical tweezers instrument with single-fluorophore sensitivity (19) to measure the rates at which short (<12 nt) DNA or RNA oligonucleotides bind and unbind to a complementary DNA strand held under tension (Figure 1A). Our investigation of the hybridization reaction as a function of oligonucleotide length and force over different ionic strengths and for DNA–DNA versus RNA–DNA duplexes paints a single, coherent picture for the energy landscape of the reaction. Using a generalized model for force-dependent rate constants, we find that the transition state is elastically similar to, though stiffer and more compact than single-stranded NA. This finding suggests a mechanism in which the hybridizing oligonucleotides must adopt pre-ordered single-stranded structures for hybridization to proceed. We provide a simple model for the elasticity of the transition state that can be used to predict the kinetics of oligonucleotide hybridization under force. Our findings help define the reaction mechanism underlying free-oligonucleotide hybridization and may also provide insights into protein- and tension-mediated hybridization reactions relevant to various NA-based bio- and nanotechnologies.

Figure 1.

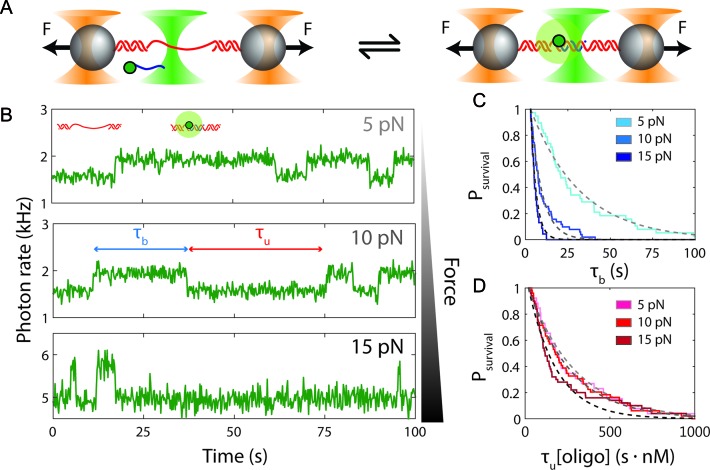
Measurement of single-oligonucleotide hybridization kinetics under force. (A) Schematic of the hybridization assay (not to scale). An engineered DNA molecule (red) containing a short, central ssDNA region flanked by long double-stranded DNA (dsDNA) handles is held under constant force by polystyrene beads (grey spheres) held in optical traps (orange cones). A fluorescence excitation laser (green cone) is focused on the central ssDNA region. Short oligonucleotides (blue) labeled with a Cy3 fluorophore at the 3′ end (green disk) bind and unbind to the complementary ssDNA sequence in the center of the tethered DNA. The binding and unbinding is observed by the fluorescence emitted from the attached fluorophores. (B) Representative time traces showing 10-nt probes binding and unbinding a DNA construct held under three constant forces (5, 10 and 15 pN, ± 0.02 pN each). The lifetimes of the oligonucleotide bound states, 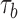and the unbound states, 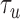, are measured from the increase and decrease of the fluorescence intensity. (C and D) The survival probabilities of the bound and unbound states over time for the three forces are shown. The probabilities are fitted to a single exponential function (dotted lines) for each force. Because the binding reaction displays second-order kinetics, the survival probabilities of the unbound states is plotted versus .

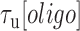MATERIALS AND METHODS

DNA construct and oligonucleotide probe design

All oligonucleotides used in this study were purchased from Integrated DNA Technology, and are listed in Supplementary Table S1. The DNA constructs in this study (Figure 1A) contained a 19-nt single-stranded (ss)DNA site flanked by two long double-stranded (ds)DNA ‘handles’ and were made by ligating together three segments: left handle (‘LH’, 1.5 kb), the insert (‘Ins’) and right handle (‘RH’, 1.7 kb). LH was synthesized from PCR amplification of the pBR322 plasmid (New England Biolabs) using a reverse primer containing biotin conjugated to the 5′ end. The PCR product was digested with PspGI, leaving a 5′ overhang. RH was similarly synthesized by PCR amplification of lambda phage DNA (NEB) using a reverse primer containing digoxigenin conjugated to the 5′ end. This PCR product was then digested with TspRI (NEB), leaving a 3′ overhang. RH and LH were then ligated to Ins, which contained a 5′ phosphate, using T4 ligase (NEB). The insert consisted of a 9-nt binding site complementary to the 9-mer oligonucleotide probe used, flanked on both sides by (dT)₅ spacers. The purpose of the poly-dT spacers was to separate the bound probes from the dsDNA handles, preventing interactions between them. To test the effect of probe-handle interactions, we designed a separate construct containing a 13-nt insert identical to the 19-nt insert described above, except that it lacked the (dT)₅ spacer on the 3′ side of the binding site (Supplementary Figure S1). The DNA and RNA probes longer than 9 nt were extended with dA or A bases, respectively, to hybridize with the spacers. All probes used had a single Cy3 fluorophore conjugated to the 3′ phosphate, with the exception of one to test the effect of the label on unbinding rate (Supplementary Figure S2).

Experimental procedure

The kinetics of DNA–DNA and RNA–DNA hybridization were measured using a high-resolution optical trap combined with a single-molecule confocal fluorescence microscope, as described previously (19). All data were collected at 22°C in a buffer containing 10–30 nM probe, 100 mM Tris, 100 mM NaCl, 0, 2 or 20 mM MgCl₂, an oxygen scavenging system to increase both tether and fluorophore lifetimes (1% glucose, 1 mg/ml glucose oxidase (Sigma-Aldrich), 0.13 mg/ml catalase (EMD Millipore)) (20,21) and a triplet-state quencher to prevent fluorophore blinking (1 mg/ml Trolox (Sigma-Aldrich)) (22). Within a flow chamber containing this buffer (19,23), a streptavidin- and an antidigoxigenin-coated microsphere (Spherotech) were trapped and tethered together in situ by the DNA construct containing the single-stranded hybridization site for the probe under investigation (Figure 1A). To confirm the proper behavior of the DNA construct, a force-extension curve was taken for each tether formed and fit to the worm-like chain (WLC) model. The construct was held at a constant tension using active force-feedback (24). The binding/unbinding of probes was observed mainly by the fluorescence signal increase/decrease from the Cy3 fluorophores on the probes (Figure 1B). In one control experiment measuring the effect of labeling on unbinding rate, we used instead the change in separation between the two traps as they were moved to maintain a constant tether tension (Supplementary Figure S2 and Supplementary Method S1). For each tethered construct, data were collected at multiple forces to eliminate any artifacts arising from variations between individual tethered molecules.

Data analysis

Lifetime distributions

Fluorescence data were saved at 100 Hz, and events were located in fluorescence trajectories by using an appropriate threshold to identify the minima and maxima of the derivative of the fluorescence signal. Since the average lifetimes varied greatly across probe lengths and forces, the sliding window over which the derivative was calculated to locate events was necessarily smaller for shorter probes. The sliding window was 0.15 s for 7-mers, 0.5 s for 8-mers and 1 s for all other probe lengths.

For each condition used (probe, force, and buffer condition), a distribution of lifetimes was obtained. In order to avoid complications from histogram bin sizes when fitting the distributions, we instead calculated the survival probability of the state in question (bound or unbound) as

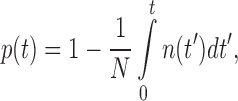(1)

(Figure 1C and D) where p(t) is the probability that the probe is still in this state at time t, N is the total number of events and n(t′) is the number of events in an interval dt′.

The survival probability was fitted to a single exponential function to obtain the rate constant for each transition (k_off for unbinding and k_on for binding). Due to the finite size of the sliding window used for calculating the derivative of the fluorescence signal, there was a lower bound in the calculated survival probabilities (i.e. p(t < t_lb) = 1 where t_lb is the lower bound). To record the lifetime of an individual event, two extrema in the fluorescence signal derivative were located: one for binding and one for unbinding. Therefore, any events shorter than twice the sliding window are inaccurately located (i.e. t_lb = 2x sliding window). To account for this, we do not consider any events shorter than t_lb, and the distributions were fitted to an exponential function shifted by t_lb:

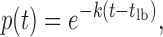(2)

where k is the rate constant of the transition in question.

Rate and equilibrium data fitting

To interpret the rate constant versus force data in Figure 2 and Supplementary Figures S3 and S4, we globally fitted the unbinding and binding data together to find the elastic parameters for the common transition state using Equations (3–5), as described in Results. A minimization routine was used that supplied ‘guesses’ for the transition state persistence length P^‡, contour length per base pair h^‡, and all zero-force rate constants for the different probe lengths (e.g. the data in Figure 2B and C had four values for k_off(0) and four values for k_on(0) for the four probe lengths) that found the values minimizing the sum of squares of the residuals. In order to obtain error bars for these values, the minimization routine itself was resampled using jackknife resampling to produce distributions of values for each parameter. The force-dependent equilibrium free energy data for DNA–DNA hybridization (Figure 2D) were fitted locally for each probe length using Equation (6) in Results with the zero-force free energies ΔG°(0) for each probe length as fitting parameters and with P_b = 53 nm, h_b = 0.34 nm/bp, P_u = 1.32 nm and h_u = 0.60 nm/nt as fixed parameters for the persistence lengths P and contour lengths per base pair h of the bound and unbound states.

Figure 2.

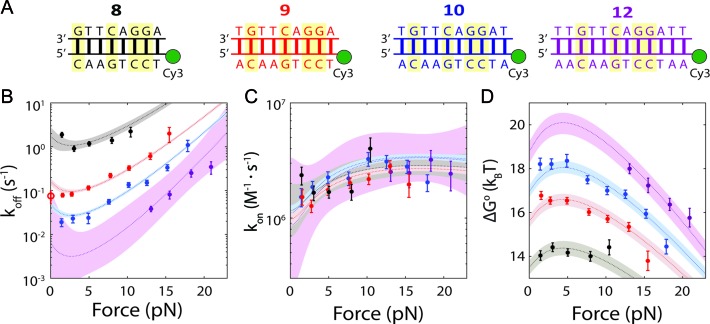
Force-dependence of oligonucleotide hybridization kinetics and thermodynamics. (A) The four oligonucleotides used in this study, bound to their complementary sequences on the DNA construct (GC pairs highlighted). (B and C) Force-dependence of the unbinding (k_off) and binding (k_on) rate constants for each probe length (error bars: s.e.m.). The dotted lines show the force-dependent model (Equations 3–5) using parameters obtained from the globally fitted data (Table 1). Open circle: measured zero-force unbinding rate constant from (11). Shaded regions represent 95% confidence intervals. (D) Force-dependence of the standard-state equilibrium free energy ΔG°(F) between bound and unbound states for each probe length. The dotted lines show the force-dependent model (Equation 6) using parameters from the literature and those determined empirically. Shaded regions represent 95% confidence intervals.

RESULTS

We measured the hybridization kinetics of short oligonucleotides of varying lengths using a recently described instrument combining high-resolution optical tweezers with single-molecule fluorescence microscopy (19). A DNA construct containing a 19-nt ssDNA site—containing a random sequence flanked by poly-dT spacers—between two long dsDNA handles was tethered between two beads held in optical traps (Figure 1A). Holding this construct at constant tension, we observed the binding and unbinding of fluorescently-labeled oligonucleotide ‘probes’ complementary to the sequence of the ssDNA site as indicated by a stepwise increase and decrease in the fluorescence signal from the single Cy3 fluorophore attached to the probes, respectively (Figure 1B). The lifetimes of each state (bound, 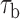; unbound, 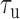) were measured from the fluorescence signal as a function of tension on the tethered DNA strand and for different probe lengths (ℓ = 8, 9, 10, 12 nt). At certain forces, binding and unbinding events could also be detected from the change in molecular extension of the tethered DNA. Lifetimes measured in this manner agreed within error of those measured by fluorescence (see Supplementary Figure S2). We made sure to work under conditions where photobleaching of the dye labeling the probe had a negligible effect on the measured probe lifetime (Supplementary Figure S3 and Supplementary Method S2). For each probe length, the measured bound- and unbound-state lifetimes followed single exponential distributions (Figure 1C and D, respectively), indicating a single rate-limiting step. We determined from the lifetime distributions the unbinding rate constant 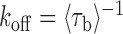and the second-order binding rate constant 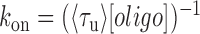, where [oligo] is the concentration of oligonucleotide probe (see Materials and Methods). The fluorescent dye had little to no effect on the unbinding rate constants (Supplementary Figure S2 and Supplementary Method S1). The length of the poly-dT spacers flanking the binding site varied (3–6 nt) across different probe lengths, but did not appear to affect the kinetics significantly. Removal of one of the spacers decreased k_off nearly 50-fold, likely from stabilizing base-stacking interactions between the bound probe and one of the dsDNA handles (Supplementary Figure S1).

Figure 2B and C show the effect of tension on the unbinding and binding rates, respectively, with each color representing a different oligonucleotide length. Unbinding rates vary strongly as a function of length and force, whereas binding rates appear independent of length and show a weak but detectable dependence on force. According to Bell's model (25), the rate constants for transitions between bound and unbound states should depend exponentially on force, as 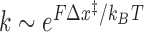, where Δx^‡ is the distance between the initial state and transition state along the mechanical reaction coordinate, k_B is the Boltzmann constant and T is the absolute temperature. Since the unbinding rate constants depend much more strongly on force than those for binding, it follows that the transition state is ‘closer’ to the unbound state than to the bound state. However, the rates do not strictly follow an exponential force dependence expected from Bell's model. The non-exponential behavior becomes apparent in the unbinding rates at lower forces (F = 1–8 pN; Figure 2B), and is consistently observed across a variety of different conditions (Supplementary Figures S4 and S5). Control experiments rule out the possibility that this non-exponential behavior is an artifact due to photobleaching of the dye labeling the probe, which could lead to an underestimate of the bound state lifetime (Supplementary Figure S3 and Supplementary Method S2). A deviation from exponential force dependence indicates that the distance from the bound state to the transition state of the reaction Δx^‡ along the pulling coordinate does not remain constant as force is applied (26,27). The need for a model allowing distances along the pulling coordinate to depend on force is also made clear by plotting the standard-state equilibrium free energy difference between bound and unbound states, obtained from the ratio of binding and unbinding rate constants, 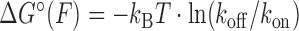, (with k_on in M⁻¹s⁻¹) versus force (Figure 2D).

To interpret the data, we adopted a generalized kinetic model in which distances are allowed to be force dependent. The force-dependent unbinding rate constant can be described by an Arrhenius-like equation:

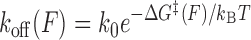(3)

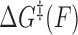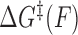where is the force-dependent activation energy for unbinding, and is the attempt rate. can be expressed as (26,28):

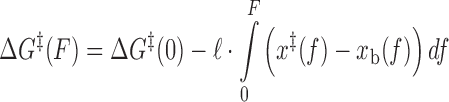(4)

where ℓ is the length of the oligonucleotide, and x^‡(F) and x_b(F) are the force-dependent extensions of the transition state and bound state per base pair, respectively. In the limit that the extension difference Δx^‡ ≡ x^‡ – x_b is force-independent, Equations (3) and (4) reduce to Bell's equation. Likewise, assuming a two-state reaction with a single barrier, the binding rate can be written as:

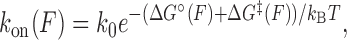(5)

in which 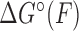is given by

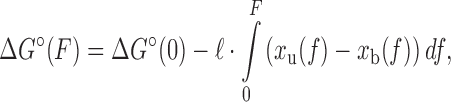(6)

where x_u(F) is the force-dependent extension of the unbound state per base pair and ΔG°(0) is the standard-state hybridization free energy at zero force.

Application of Equations (3–6) to the data requires us to model the force dependences, i.e. elastic properties, of the bound, unbound and transition states through the functions x_b(F), x_u(F), and x^‡(F), respectively. The bound and unbound states correspond to dsDNA and ssDNA (Figure 1A), whose elastic properties are well established for long polymers, though contested at short length scales (29–31). Nevertheless, our prior measurements of the extension change between short (9-nt) ssDNA and dsDNA (19) indicate that the standard, long-polymer WLC model of elasticity (32–34) is sufficient to describe the data across most of the force range assayed. We thus modeled x_b(F) with the WLC model, using a persistence length P_b = 53 nm and helix rise h_b = 0.34 nm/bp, as reported for dsDNA (34,35). For x_u(F), we used force-extension curves of our construct to constrain WLC parameters. Fitting to the WLC model using a fixed contour length per nucleotide h_u = 0.60 nm/nt yielded an optimal value of the persistence length P_u = 1.32 ± 0.07 nm (Supplementary Figure S6 and Supplementary Method S3), consistent with values reported in the literature for short strands of ssDNA (36–40). We validated our models for x_b(F) and x_u(F) against the force-dependent equilibrium free energy difference ΔG°(F). As shown in Figure 2D, the data are fitted well to Equation (6) with no adjustable parameters other than the zero-force free energy for each probe length, ΔG°(0). Moreover, the values for ΔG°(0) are in very good agreement with those reported for the equilibrium hybridization free energies of the specific oligonucleotide sequences we used (Supplementary Figure S7 and Supplementary Method S4) (41,42). This good agreement also shows that the poly-dT spacers and dsDNA handles in our construct have a minimal effect on the oligonucleotide hybridization reaction.

We next considered x^‡(F). A number of models have been proposed for the hybridization transition state (13,43,44), but none have been verified directly. In one candidate model (13), the transition state corresponds to a nucleated duplex where a few native base-pairs have formed. To test this nucleated duplex model, we fitted the unbinding and binding rates globally using a force-dependent extension in Equations (3–5) in which n native base-pairs (dsDNA) are formed and ℓ – n remain unpaired (ssDNA) (Supplementary Figure S8 and Supplementary Method S5). However, we found fits to the data in Figure 2B and C (Supplementary Figure S8) to be poor (reduced chi-squared χ²_red = 6.1), failing to reproduce the force dependence of the binding rates and yielding n = 0 native base pairs, corresponding to a purely ssDNA transition state, a model proposed by Ho et al. (43). We thus considered another model where the transition state behaves as a homogeneous polymer with unique elastic parameters. For simplicity, we assumed that the transition state extension scales linearly with oligonucleotide length over the narrow range investigated (8–12 nt). Globally fitting the binding and unbinding rate constant data (Figure 2B and C) to this model yielded better fits (reduced chi-squared χ²_red = 2.9) with values of P^‡ = 2.6 ± 0.2 nm and h^‡ = 0.54 ± 0.01 nm/nt (s.e.m.; see Materials and Methods). Although these values are similar to those reported for ssDNA (36–39), they differ from those used to describe the unbound state in our data, indicating that the transition state is close in form to ssDNA, except stiffer (higher P) and more compact (lower h). This difference is reflected in the weak force-dependence of the binding rate data (Figure 2C).

To confirm the above model, we devised an alternate method of quantifying the transition state force dependence. As done previously for RNA hairpins (27,45), we solved Equations (3–6) for the transition state extension to obtain an expression to extract x^‡(F) directly from our unbinding rate constant data and the validated model for the bound state extension x_b(F):

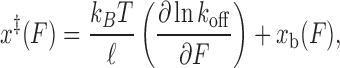(7)

and a similar expression in terms of the binding rate k_on and unbound state extension x_u(F). This exercise allows us to visualize directly the transition state force dependence and also validates the assumption made above that the transition state extension scales linearly with probe length over the range assayed (Supplementary Figure S9). Figure 3 shows the force-extension curve, x^‡(F), that results when scaling all transition state extensions by length and averaging them together. Although x^‡(F) lies close to ssDNA, it is better fit by the homogeneous polymer model described above and used in the global fits.

Figure 3.

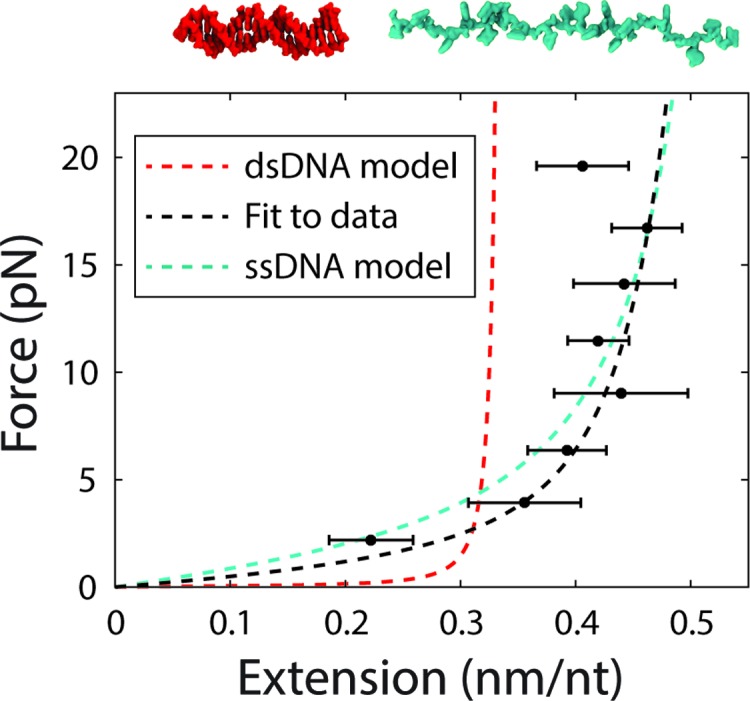
Force-extension curve of the transition state for hybridization. The end-to-end extension of the transition state was calculated from Equation (7). The model for the transition state using the fitted parameters for P^‡ and h^‡ (black dotted line) is plotted alongside the models for dsDNA (red dotted line) and ssDNA (cyan dotted line) for comparison.

To test the generality of our findings, we repeated these measurements not only at high ionic strength (high Mg²⁺) but also with an RNA hybridizing probe in place of DNA (Supplementary Figures S4 and S5). The high ionic strength also allowed us to extend our measurements to ℓ = 7 nt by reducing the rate of unbinding (Supplementary Figure S10). Under all conditions the elastic parameters for the transition state were comparable to each other, indicating a similar transition state structure (Table 1).

Table 1. Obtained parameters from fitting of data.

	DNA, 0 mM Mg2+	DNA, 20 mM Mg2+	RNA-DNA, 20 mM Mg2+
P‡ (nm)	2.6 ± 0.2	1.92 ± 0.08	2.7 ± 0.5
h‡ (nm/nt)	0.54 ± 0.01	0.54 ± 0.01	0.53 ± 0.01
Pu (nm)	1.32 ± 0.07	1.07 ± 0.05	1.07 ± 0.05

DISCUSSION

The kinetics of any two-state reaction are determined by the transition state that is visited when passing from one state to the other. Here, we have characterized the transition state for nucleic acid hybridization by measuring the kinetics of the reaction under force applied to the target strand. Across the range of conditions assayed, our analysis indicates a transition state that is similar to ssDNA. At first glance, our findings appear to stand in contrast to those in prior studies. Strunz et al. (13) extracted the rates of oligonucleotide melting from force-ramp measurements where force was applied across opposite 5′ ends of short duplexes. Fitting the force-dependent melting rates to Bell's equation, they determined that the distance from the bound state to the transition state, Δx^‡, was a constant ∼1 Å per bp of the duplex. However, as discussed above, Bell's model can be inappropriate in many cases despite its common use. Our binding and unbinding rates show clear non-exponential behavior over our force range (Figure 2B and C), which indicates that Δx^‡ is not constant. If we consider only forces >10 pN such as those assayed in Strunz et al., our measured unbinding rate constants display approximate single-exponential behavior (Figure 2B). Fits of the high-force data to Bell's equation provides us with a linear relation of Δx^‡ = 1.4 ± 0.2 Å/bp, similar to that of Strunz et al. and in reasonable agreement with our prior estimate also using Bell's model (19). Our generalized model, which allows for force-dependent distances to the transition state, is demonstrably better at fitting the data over the entire range of forces assayed, but remains consistent with the results of Strunz et al. in the high force range. Nevertheless, our findings illustrate the caution needed in interpreting parameters extracted from Bell's model.

Our model approximates Bell's equation in the high force range and captures the deviations from exponential force dependence in the rates k_off and k_on observed at lower forces (<10 pN). One question our results raise is how the rates behave at and near zero force. Our model predicts a ‘roll-over’ in k_off below ∼1.5 pN (Figure 2B, Supplementary Figures S4 and S5), suggesting that low forces would stabilize the DNA duplex, a result that has been discussed theoretically (43,46). The lack of data below ∼1.5 pN in our experiments makes it difficult to determine this behavior directly. Single-molecule FRET measurements of hybridization performed by Cisse et al. (11) at zero force using an identical sequence to the 9-nt probe used here and under similar experimental conditions yield a k_off ranging between 0.05 to 0.1 s⁻¹, which compares well to our 9-nt probe data (Figure 2B). However, the FRET result suggest that the force-dependence of the unbinding rate constants vanishes below 1.5 pN, in disagreement with our model. It is possible that the hybridization reaction coordinate no longer projects well onto the pulling coordinate (i.e. the end-to-end extension) at these forces, resulting in force-independent rates (17). Assays more sensitive to this low-force range will be necessary to quantify this behavior accurately.

An important question is the nature of the transition state. As shown in our analysis above, our data are best described by a simple homogeneous worm-like polymer. Some studies have proposed that the hybridizing strands must first be ‘pre-aligned’ or ‘pre-ordered’ prior to base pairing (44,47,48). Such ‘pre-ordering’ may be reflected in the persistence length for the transition state, which is larger than that of the unbound state. This means that the transition state is slightly stiffer than the unbound state. We speculate that some amount of single-stranded base-stacking or electrostatic stiffening from the increased number of backbone phosphate charges as two strands approach one another could lead to an increased stiffness (49). The ‘pre-aligning’ mechanism is supported by the observation that annealing is not diffusion-limited (47) and that only one in 100–1000 diffusional encounters successfully produces a duplex (44). The binding rates we measure, extrapolated to zero force, range between 10⁶–10⁷ M^–1·s^–1 (across the range of Mg²⁺ concentrations assayed; Supplementary Figure S10), consistent with this picture (Figure 2C). Presumably, the low success rate arises because the strands must be in the correct register and alignment with respect to one another to anneal successfully. Although this configuration is entropically unfavorable, a simple, polymer elasticity-based estimate of the probability that a 5–13 nt oligonucleotide in solution is extended and aligned with the strand under tension is consistent with the 10⁻²–10⁻³ success probabilities previously measured by fluorescence correlation spectroscopy (FCS) (44) (Supplementary Method S6). Our observation that the binding rates increase with force (Figure 2C, Supplementary Figures S4 and S5) also suggests that force may pre-align the tethered strand by extending it, promoting hybridization. Further characterization will be necessary for a more quantitative comparison to our data. We note that the dependence of the hybridization reaction on polymer elasticity may also apply to protein folding, which has been proposed to be driven mainly by the elastic properties of the polypeptide chain (50).

Irrespective of the detailed transition state structure, it is important to note that our assumption that the transition state extension scales linearly with probe length can only hold over short lengths, since it is unreasonable to expect long strands (>>10 nt) to pre-order before annealing. We can use our simple estimate of the probability that a short ssDNA length is aligned with the strand under tension above to place a bound on the maximum length that can be pre-aligned. Based on this model (Supplementary Method S6), probabilities that a segment ≳13 nt is pre-aligned to the tethered strand must be ≲10⁻³. This provides evidence that the unique structural properties of the transition state we report are confined to lengths within the range of those used in this study (8–12 nt).

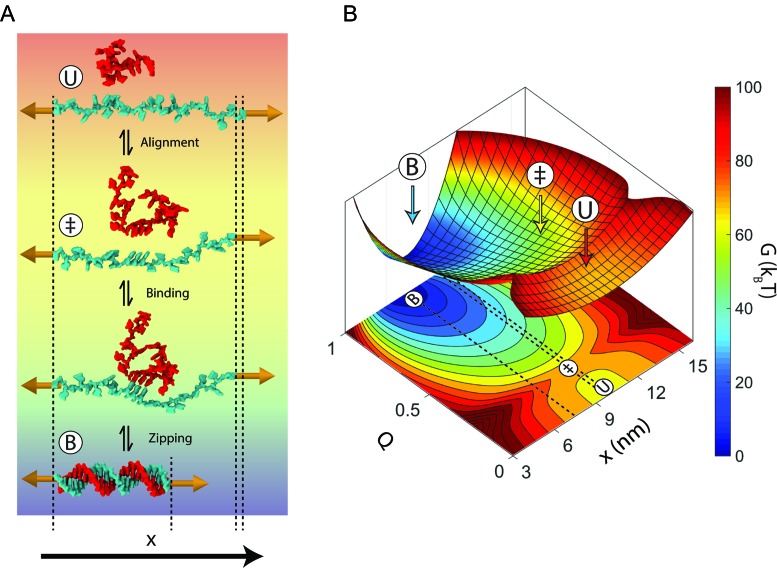
Using our generalized model for the transition state, we can construct a schematic energy landscape that encapsulates the hybridization reaction (Figure 4). The extensions of the bound, unbound and transition states are calculated from the elasticity models described above (Table 1). We note that there are forces at which the equilibrium states have the same extension as the transition state (bound, ∼3 pN; unbound, ∼12 pN; Figure 2B, C and Figure 3), making the activation barrier disappear in the extension coordinate. This behavior implies that extension is a poor coordinate at these forces and that a simple 1D model of the energy landscape is insufficient (17). It is therefore helpful to introduce a second coordinate, Q, representing the number of native contacts formed to illustrate the hybridization reaction (51). The free energy difference ΔG° and extension differences between the bound and unbound states are taken directly from our data (Figure 2D), whereas Q is schematic. The total free energy difference between the bound state and the transition state 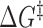was calculated from the zero-force unbinding rate constants, assuming an intrinsic rate constant k₀ = 10⁷ s⁻¹, in accordance with literature values (7,8,36) (Supplementary Figure S7).

Figure 4.

Model for nucleic acid hybridization. (A) Schematic depicting nucleic acid hybridization of a 22-nt oligonucleotide (red) to a complementary strand (cyan) under a force of 15 pN. In the unbound state (U), the strand under tension encounters a random-coil oligonucleotide. Most encounters between these two strands do not result in duplex formation because they are not aligned properly with respect to one another. When both strands transiently form a short stretch of aligned nucleotides (‡), they are prepared to bind to one another. The two strands then bind and rapidly zip together to form the bound-state duplex (B). The dsDNA in this schematic was created using Visual Molecular Dynamics (VMD) (59) using Protein Data Bank (PDB) entry 1BNA. (B) Model energy landscape corresponding to the schematic in A at 15 pN. Two reaction coordinates are shown: the end-to-end extension of the strand held under tension, x, and the fraction of native duplex contacts formed, Q. Dotted lines on the x-Q projection are shown to clarify the end-to-end extension of each state.

A model of the transition state as a pre-ordered, single-stranded nucleic acid is attractive as it may help explain the mechanism of protein-mediated hybridization in the cell. Oligonucleotides do not hybridize very quickly on their own, but a protein may speed up the reaction by pre-ordering a single-stranded nucleic acid for binding a target. There are several noteworthy examples of such proteins: crystal structures of DNA-degrading CRISPR-Cas9 and RNA-silencing Argonaute reveal a short stretch of ‘seed’ ssNA (RNA for Cas9 and human Argonaute-2, DNA for some bacterial Argonautes) pre-ordered in preparation for binding their target (52–55). Our results suggest that this convergent ‘seed’ mechanism may not only increase the specificity of the guide for its target, but also the rate at which they bind by mimicking the transition state for hybridization.

We also expect our results to help in the design and modeling of DNA nanotechnology. For example, recently developed DNA-based force sensors (56) would benefit from a detailed model for force-dependent melting rates, which has been lacking to-date (28). Nucleic acid-based nanomachines are another example. Most nanomachines rely on strand-displacement, where an invading strand displaces an incumbent strand (57). This process is generally very slow, but kinetic control may be possible through application of force on the incumbent strand to increase its off-rate (58). We thus anticipate our model for the force- and length-dependence of hybridization rate constant to be useful in predicting and designing force-sensitive nucleic acid-based nanostructures.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Science Foundation [MCB-0952442 (CAREER) and PHY-1430124 (Center for the Physics of Living Cells)]; National Institutes of Health [R21 RR025341]. Funding for open access charge: National Science Foundation [PHY-1430124].

Conflict of interest statement. None declared.