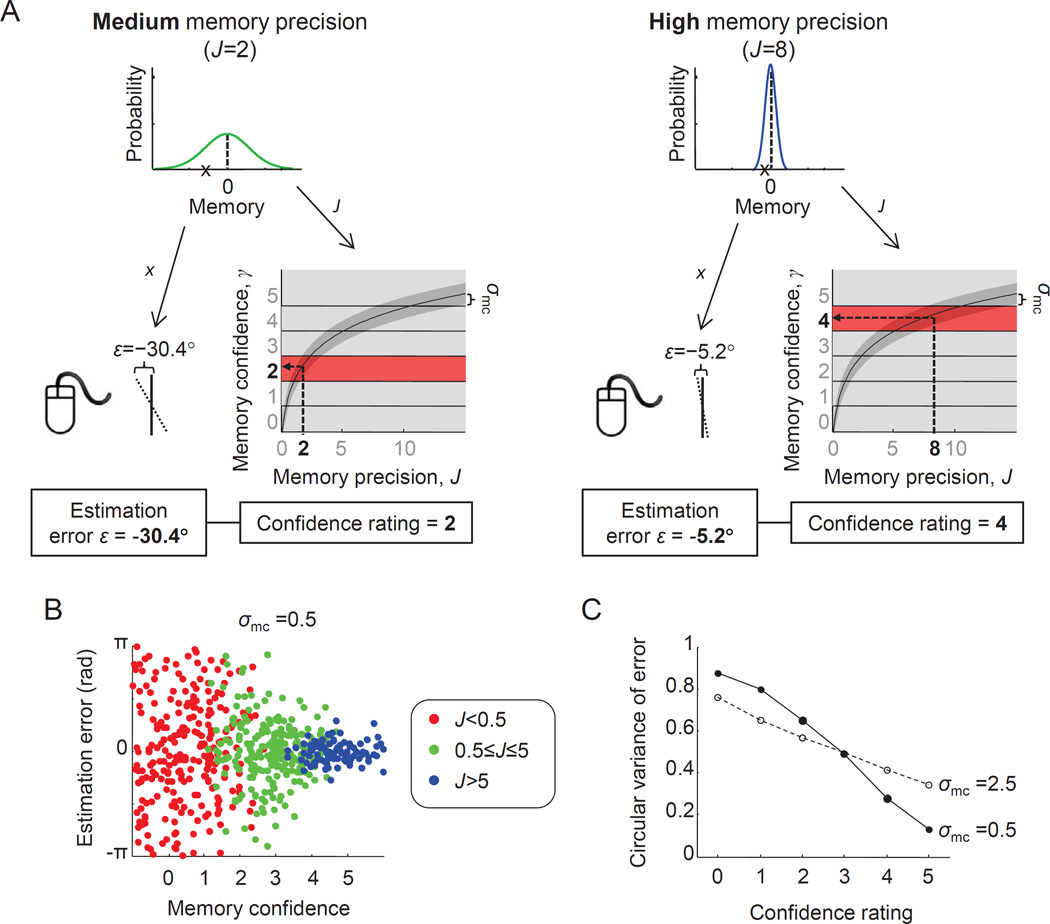
Figure 2. A Fechnerian model of working memory confidence.

(A) Illustration of how our proposed model jointly produces a near-continuous estimation error and a discrete confidence rating in a delayed-estimation experiment. The example on the left shows a trial in which a memory is encoded with medium precision (J=2) and the one on the right a trial in which it is encoded with high precision (J=8). Precision, J, determines the width of the noise distribution and is also the variable that is mapped – through Fechner's law – to a confidence rating. Hence, J affects both the subject's estimation error and her confidence. (B) Simulation results from 1000 trials, with J drawn on each trial from a gamma distribution with a mean of 1.5 and a scale parameter of 10. Each dot shows the estimation error (y-axis) and confidence (x-axis) of one trial. Trial-to-trial variability in J induces a negative correlation between estimation error and confidence: when precision is low (red), estimation errors tend to be larger and confidence tends to be lower than when precision is medium (green) or high (blue). (C) Circular variance of the error as a function of confidence rating in the same simulation, for two different values of σ_mc. The strength of the negative correlation depends on the amount of metacognitive noise.