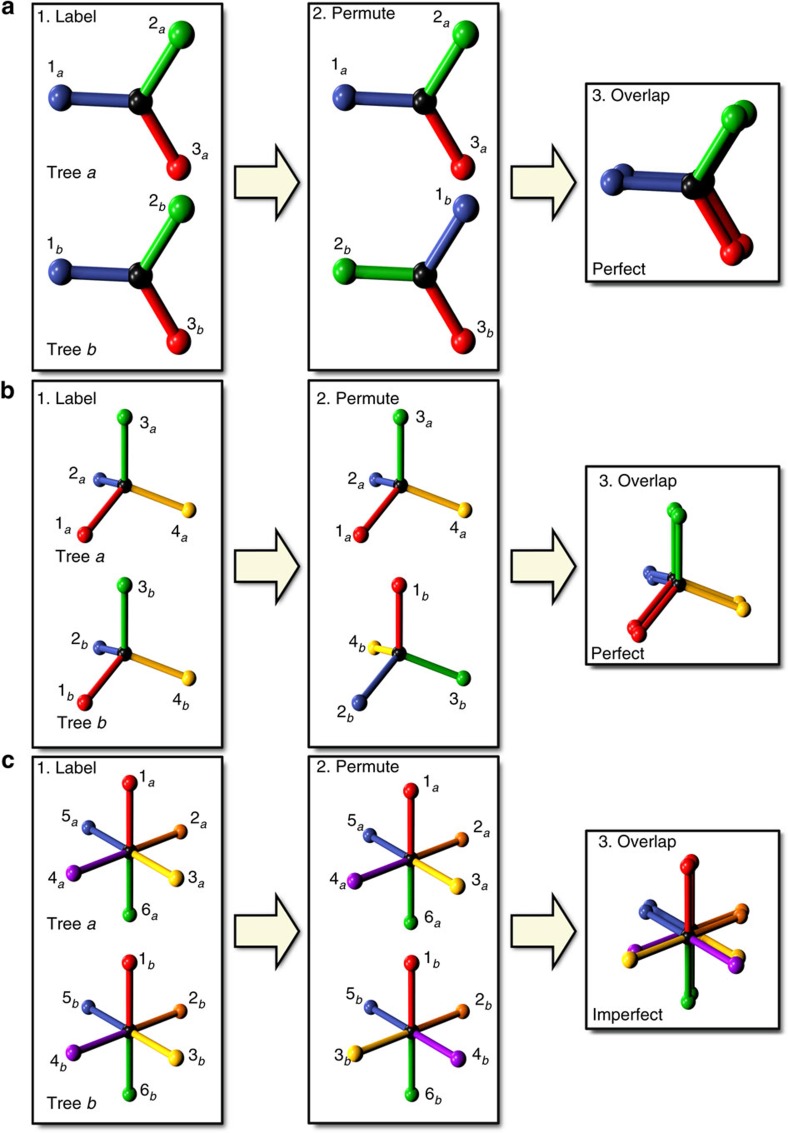
Figure 2. Comparison of 1-trees illustrated with trihedra, tetrahedra and octahedra.

Two identical trihedral trees (a) are labelled by their edges. The edges of tree b are then permuted. Tree b can then be rotated around the edge 3_b axis and made to perfectly overlap tree a. Similarly, two identical tetrahedral trees are labelled (b), and then the edges of tree b permuted. Reflection of tree B in the plane of edges 2_b and 4_b, followed by rotation around the new edge 3_b axis, brings the two trees into alignment. Two identical octahedral trees (c) can also be compared. We apply a permutation to tree B's edges. When overlapped, the two trees are now mismatched; their yellow and purple edges are not aligned and cannot be made so by any congruent transformation without creating a new mismatch.