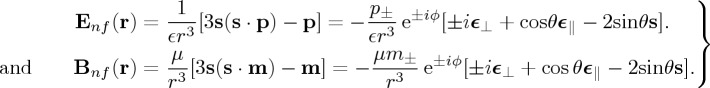Chiral optical fields: a unified formulation of helicity scattered from particles and dichroism enhancement

Abstract

We establish a general unified formulation which, using the optical theorem of electromagnetic helicity, shows that dichorism is a phenomenon arising in any scattering—or diffraction—process, elastic or not, of chiral electromagnetic fields by objects either chiral or achiral. It is shown how this approach paves the way to overcoming well-known limitations of standard circular dichroism, like its weak signal or the difficulties of using it with magnetodielectric particles. Based on the angular spectrum, representation of optical fields with only right circular or left circular plane waves, we introduce beams with transverse elliptic polarization and possessing a longitudinal component. Then, our formulation for general optical fields shows how to enhance the extinction rate of incident helicity (and therefore the dichroism signal) versus that of energy of the light scattered or emitted by a particle, or vice versa.

This article is part of the themed issue ‘New horizons for nanophotonics’.

1. Introduction

Chiral fields are acquiring increasing attention due to their potential as probes of matter at the nanoscale [1–9], of which life molecules are of paramount importance, or as high information capacity signals in communication channels [8,10–13] with control and transfer of angular momentum, which includes recently developed structured materials and metasurfaces. The conservation of the electromagnetic helicity of wavefields (or, equivalently, chirality when they are quasi-monochromatic; we shall indistinctly use both terms for such fields) [4,6,14,15] was recently shown [16] to lead to a new optical theorem which characterizes the excitation and emission of field helicity—or chirality—by bodies, and that we believe should play a growing relevant role in coming years with the progress of research on applications of twisted light.

In this context, we pointed out [16] that circular dichroism (CD) [17–19], i.e. the difference in absorption—or emission—of energy by molecular objects according to the handness of circularly polarized light (CPL), is a particular case of this optical theorem for scatterers, and hence it does not need to resort to quantum mechanics as usually done in its standard formulation. Thus, this phenomenon is just a consequence of the conservation of helicity of electromagnetic fields on scattering.

Different studies have discussed what kind of structures are necessary to produce chiral fields and whether CD requires those objects being chiral. However, some works have recently shown that this effect can be obtained with achiral objects [20]. Moreover, separating the existence of chirality from dichroism effects may be a problem in some observations [21,22]. Nonetheless no general and unified framework, not limited to particular structures, has been yet established.

In this paper, we show that dichorism is not only an effect due to absorption and e.g. fluorescent re-emission by molecules; but it constitutes a property of any scattering interaction, elastic or not, of electromagnetic twisted fields. Thus, based on the aforementioned optical theorem for the helicity, we generalize the concept of dichroism and demonstrate how it appears not only with CPL waves, but also with arbitrary chiral optical fields. This allows the design of an illumination that enhances the information content of the scattered signal, overcoming well-known limitations of standard CD detection, like its weak signal or its difficulties with magnetic objects [23].

For comprehensiveness, we next present a summary of concepts associated with the helicity and its optical theorem. Then, we show how general optical fields, expressed by its angular spectrum of plane waves, may be represented as a superposition of CPL components of right handed (RCP) and/or left-handed (LCP) polarization. This explicitly formulates in a quantitative manner previous descriptions of helicity of general wavefields, and permits us to introduce a class of elliptically polarized hypergeometric beams, as well as their Hermite and Laguerre derivations, which naturally appear when such representation is applied to a Gaussian angular spectrum.

We then establish how the helicity optical theorem, applied to arbitrary fields and to chiral optical beams in particular, leads to a unified generalization of the theory of dichroism. A first consequence of which is to put forward the way of enhancing either the extinction of helicity and hence the dichroic signal, or the extinction of intensity. Such configurations and detections are amenable to future experiments.

(a). The excitation of helicity

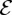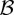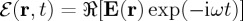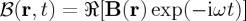Quasimonochromatic fields have a time-harmonic dependence, i.e. their electric and magnetic vectors and are described in terms of their complex representations E and B as: and , respectively. ℜ denoting real part. Then, the two fundamental quantities we deal with in this work are the helicity density, 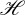, and the density of flow of helicity, 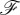, which in a non-absorbing dielectric medium of permittivity ϵ, permeability μ and refractive index 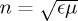are [6,16]: 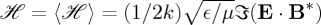and 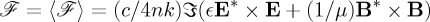. 〈⋅〉 denoting time-average, ℑ meaning imaginary part and k=nω/c. It must be recalled that for these time-harmonic fields 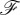coincides with the spin angular momentum density and is [4,6,15,16] k² times the flow of chirality. On the other hand, 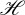is k² times the chirality. Also, they fulfil the continuity equation [4,6,15,16]: 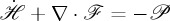. Where the helicity dissipation on interaction of the fields with matter is represented by .

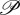Let a quasi-monochromatic field, whose space-dependent complex representation is denoted as E_i,B_i, illuminate a particle which we consider magnetodielectric and bi-isotropic [24,25], dipolar in the wide sense, i.e. if for instance it is a sphere, its magnetodielectric response is characterized by its electric, magnetic and magnetoelectric polarizabilities: α_e, α_m, α_em, α_me, given by the first-order Mie coefficients as α_e=i(3/2k³)a₁, α_m=i(3/2k³)b₁, α_em=i(3/2k³)c₁, α_me=i(3/2k³)d₁=−α_em. a₁, b₁ and c₁=−d₁ standing for the electric, magnetic and magnetoelectric first Mie coefficients, respectively [25,26]. The condition α_em=−α_me expressing that the object is chiral. We remark that by particle we shall understand small objects such as atoms, molecules, material macroscopic particles or quantum dots.

The electric and magnetic dipole moments, p and m, induced in the particle by this incident field are

1.1

At any point outside this scattering object, the total field is written as E(r)=E_i(r)+E_s(r), B(r)=B_i(r)+B_s(r). The subindex s denoting the scattered, or radiated, field.

The optical theorem that rules the conservation of helicity described by the above-mentioned equation, 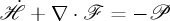, is [16]

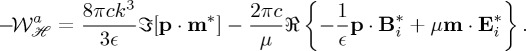1.2

On the left side of (1.2), 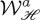is the rate of dissipation by the particle of the incident field helicity. It comes from the integration of in a volume that contains this body. On the other hand, from the Gauss divergence theorem the terms in the right side of (1.2) arise from the flow of 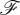across a surface that contains the particle [16]. The first of these terms represents the total helicity scattered or radiated by the object, whereas the second one constitutes the extinction of helicity of the incident wave on scattering. This latter extinction term should be used for determining both dissipated and radiated, or scattered, helicity by a dipolar particle in an arbitrary, homogeneous or inhomogeneous, embedding medium. To emphasize this interpretation, we recall its analogy with the well-known optical theorem for energies [27]

1.3

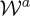being the rate of energy absorption from the illuminating wave. In the right side of (1.3), the first term constitutes the total energy scattered by the dipolar object, whereas the second one represents the energy extinguished from the illuminating field, or rate of energy excitation in the scattering object.

Henceforth, we remark the analogous role played by the right-side terms in both optical theorems (1.2) and (1.3). As it is well known, (ω/2)ℑ[p⋅E*+m⋅B*] has been extensively employed for characterizing dipole optical interactions [28–30]. We thus expect that progress on research of radiation–matter interactions with chiral fields will give rise to a growing use of the helicity extinction in equation (1.2): 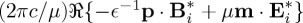. Based on this reasoning, we find it natural to introduce an enhancement factor 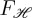for the emission of helicity in analogy with the Purcell factor for a radiating electric and/or magnetic dipole: F=1+(3/2k³)[ℑ{p⋅E*+m⋅B*}]/[ϵ⁻¹|p|²+μ|m|²], viz.

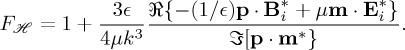1.4

In this connection, and analogously to the complex Poynting vector theorem of energy conservation (see section 6.10 of [31] and also [21,22]), the integration of the above-mentioned continuity equation for a lossy particle of volume V with constitutive parameters ϵ=ϵ_R+iϵ_I and μ=μ_R+iμ_I, in the absence of induced currents, yields (1.2) with: 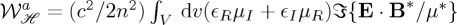; which links fields in, or close to, the object with those in any other region of space; in particular in the far-zone.

2. The angular spectrum of circularly polarized plane wave components

We address the wide variety of fields propagating in a half-space z>0, or z<0, free from sources, represented by an angular spectrum of plane waves [32,33]. This includes optical fields. Such representation of either incident and scattered fields, with subindex i and s respectively, is

2.1

The integration being done on the contour 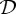that contains both propagating and evanescent waves [32,33]. s=(s_⊥,s_z) is the unit wavevector of the plane wave component of amplitude e_i,s(s_⊥) and b_i,s(s_⊥) , where s_⊥=(s_x,s_y,0) and 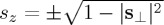if |s_⊥|²≤1 (propagating components), and 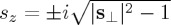if |s_⊥|²>1 (evanescent components). 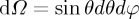. 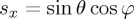, , 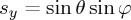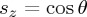. 0≤φ≤2π, 0≤θ≤π/2 for propagating components and θ=π/2−iδ, 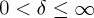for evanescent components. The + or − sign in s_z applies according to whether propagation is in z>0 or z<0, respectively. We shall assume the first case. For z<0, the results are similar. In general, all plane wave components are elliptically polarized. For the incident and scattered fields one has: b_i,s(s_⊥)=ns×e_i,s(s_⊥), e_i,s(s_⊥)⋅s=b_i,s(s_⊥)⋅s=0. The complex amplitudes of the scattered, or radiated, field angular spectrum being

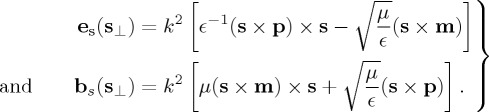2.2

For each plane wave component with wavevector ks of either the incident or the scattered field (2.1), we consider an orthonormal set of unit vectors (cf. figure 1) {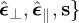 from which we define an helicity basis of rotating vectors: 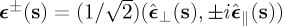, ϵ^±*(s)⋅ϵ^∓(s)=0. Then each incident or scattered component complex amplitude is expressed as the sum of a left-handed (LCP, sign ‘+’) and a right-handed (RCP, sign ‘−’) circularly polarized plane wave in its corresponding framework { 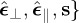according to

2.3

and

2.4

With equation ∇⋅E=0 imposing according to (2.1) that ϵ^±(s)⋅s=0. In this representation, the helicity density of each incident or scattered plane wave component reads

2.5

That is, as the difference between the LCP and RCP intensities of this angular component of wavevector ks. S₃(s_⊥) is the fourth Stokes parameter [27,34]. Also 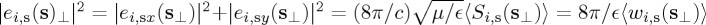. 〈S_i,s(s_⊥)〉 and 〈w_i,s(s_⊥)〉 representing the time-averaged Poynting vector magnitude and electromagnetic energy density, respect- ively: 〈w_i,s(s_⊥)〉=〈w_ei,s(s_⊥)〉+〈w_mi,s(s_⊥)〉 . 〈w_ei,s(s_⊥)〉=(ϵ/16π)|e_i,s(s_⊥)|², 〈w_mi,s(s_⊥)〉=(1/16πμ)|b_i,s(s_⊥)|².

Figure 1.

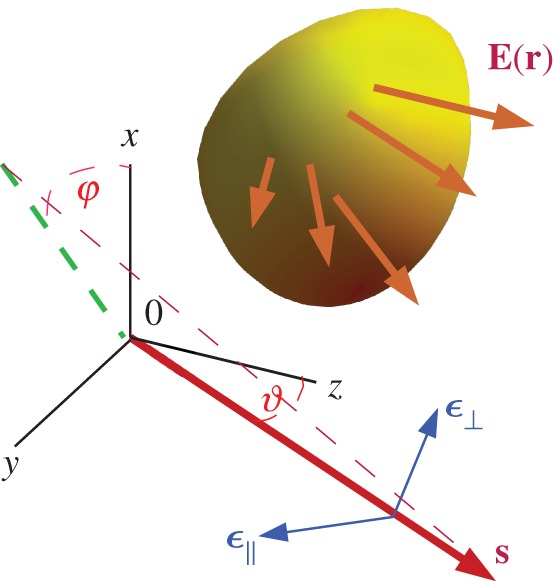
A field E(r), with wavefront shown by the brown-yellow surface, propagates into the half-space z>0 along arbitrary directions (light-brown arrows). In the 0XY Z framework, the propagation vector along s of each plane wave component of E(r) has polar and azimuthal angles θ and ϕ. The polarization of each of these plane waves is characterized by the orthonormal system {ϵ_⊥,ϵ_∥,s}. The unit vector ϵ_∥ is in the polar plane containing both s and its projection(green broken line) on OXY , and points in the rotation sense of θ. On the other hand, ϵ_⊥ is normal to this plane and points against the sense of rotation of ϕ. (Online version in colour.)

Therefore, for the incident or the scattered field we have from (2.1), (2.3) and (2.4) the following splitting into LCP and RCP waves

2.6

and

2.7

Assuming the particle chiral, α_em=−α_me, and introducing equations (2.7) into (1.1) we write

2.8

With

2.9

And substituting (2.1) into (2.9), we see that p_±(r) and m_±(r) also admit an angular spectrum representation like (2.1), their respective angular spectra being

2.10

So that from (2.10), (2.8) and (2.2), we obtain for the scattered field angular spectrum

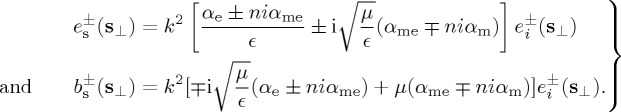2.11

We obtain the helicity densities 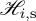for either the incident or scattered fields by introducing (2.3) and (2.4) into (2.1), and inserting the result into the definition introduced in §1a: 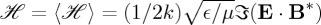. Then since after taking imaginary parts the cross-terms containing the integrand factors 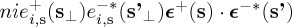and 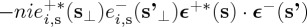cancel each other, we finally get

2.12

Equation (2.12) introduced in the optical theorem for the helicity, (1.2), accounts for all chirality effects due to the interaction of waves with dipolar particles, both in the propagating region (real 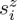) of the angular spectrum, as in the evanescent domain (imaginary 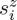). The latter applies in particular for the interaction of plasmon polaritons with particles on metallic surfaces.

Expressions (2.12) are of particular importance in the far zone , where [32,33]

2.13

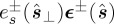plays the role of the CPL complex amplitude for a radiated, or scattered, field, and 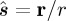now belongs to the domain of propagating components only. Dropping the sub-indices i,s to simplify notation, equations (2.12) and (2.13) lead for either the incident or the scattered field to

2.14

And their density of flow of helicity is , which in agreement with the conservation of helicity, expresses on integration in a large sphere surrounding the scatterer that the outgoing helicity flow of the field across any plane z=constant, or closed surface, outside the scattering volume, which equals the flow of helicity across any sphere at infinity, is equal to c/n times the total helicity enclosed by that sphere: 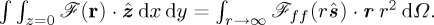Where now the solid angle Ω spans on the whole sphere of real angles only. Taking into account (2.12), and in analogy with the flow of energy [32,33], one sees that the evanescent components do not contribute to the flux of helicity across the plane z=0 in the half-space z≥0.

(a). A particular case: incident elliptically polarized plane wave

The significance of the optical theorem (1.2) for the helicity—or chirality—of wavefields is illustrated considering one of the simplest and most employed configurations: one elliptically polarized incident plane wave impinging on a dipolar particle with wavevector ks_i along OZ. According to (2.3) and (2.4) the fields are . .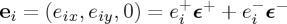

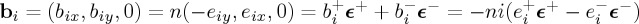So that the incident helicity density reads

2.15

Also, according to (2.8) and (2.9): .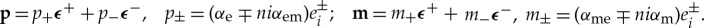

On introducing, these dipole moments and fields into the optical theorems of helicity (1.2) and energy (1.3), they yield for the rate of helicity and energy extinction

2.16

and

2.17

respectively. Equation (2.16) is identical to the CD law, usually mechanoquantically formulating molecular absorption and fluorescence effects [18]. However, equations (2.16) and (2.17), obtained from classical electrodynamics, include the rate of helicity and energy dissipation both by absorption and scattering (or diffraction), and generalize the CD theory to any wide sense dipolar ‘particle’ or structure.

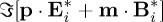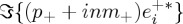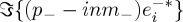In other words, the CD phenomenon is not only characterized by the operation of taking the difference of energy absorption and emission by chiral molecules as they are separately illuminated by RCP and LCP waves; i.e. as this absorbed energy is and , respectively, as usually considered so far [17–19]. But CD is also, and fundamentally, one of the physical manfestations of the conservation law of electromagnetic helicity—or chirality—and is represented by the left-side extinction term of (2.16), 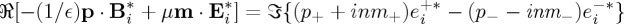of the helicity optical theorem (1.2); being involved in any scattering and/or absorption process of LCP and RCP electromagnetic waves, thus characterizing the rate of extinction helicity, or chirality. In addition, as shown by equation (2.10) and (2.16), CD arises not only due the chirality of the scattering object, represented by α_me, but also and primarily by the mere induction of their electric and/or magnetic dipoles.

Hence it is not surprising that the ratio of the extinction of incident field helicity (2.16) and energy (2.17) is identical to the well-known dissymmetry factor of CD [4,17,19]. Moreover, adding and substracting (2.16) and (2.17) yield the energy excitation by extinction of the respective LCP or RCP component of the incident elliptically polarized light according to the dipole handness p_± and/or m_±:

2.18

(b). The special case of an incident circularly polarized plane wave

Let the field incident on the particle be just one CPL component, either LCP or RCP, then and p=p_±ϵ^±, m=m_±ϵ^±, and (2.18) lead to

2.19

and

2.20

From which we obtain

2.21

Thus, apart from a constant factor, for CPL incidence the scattered helicity equals in modulus the scattered energy plus the rates of dissipation of helicity and energy, and has a sign that depends on the handness of the incident light. Of course (2.19)–(2.21) are consistent, as they should, with equations (2.16) and (2.17), which for CPL become

2.22

A comparison of (2.22) with (2.16) and (2.17) shows that the excitation of the particle by both the LCP and RCP components of an elliptically polarized plane wave is equivalent to performing two observations separately: one with an LCP plane wave only, and another one with only RCP (each of which is ruled by (2.22) with the corresponding sign), and then substracting or adding the respective excitations given by the left sides of (2.22). This operation reproduces the left side of (2.16) and (2.17), respectively. In other words, equations (2.16) and (2.17) show that the LCP and RCP components of an incident elliptically polarized plane wave do not interfere and, hence, interact independently of each other with the particle.

As regards equation (2.20), because often in molecular spectroscopy |m_±|≪|p_±|, the value of 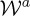and/or 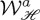contributes to that of |p_±|. Nonetheless, equation (2.20) is also compatible with the electric and magnetic dipoles excited by CPL light, and the absorption rates, fulfilling

2.23

Hence this is a sufficient condition for an electric–magnetic dipole to emit chiral light. Particularly remarkable is this latter case is when the dissipation rates of helicity and energy either cancel each other, or the particle introduces no energy or helicity losses, 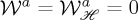, so that all energy and helicity extinguished from the incident field are re-radiated by elastic scattering. As seen from (2.20), in that case 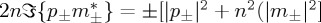, which states that then the optical theorems for helicity, equation (2.16), and energy, equation (2.17), are equivalent, and the scattered helicity is proportional to the scattered intensity and has a sign that depends on the handness of the incident light, whereas the density of helicity flow (spin) is proportional to that of energy flow (Poynting vector). Thus in such a situation the optical theorems for helicity (1.2) and energy (1.3) are equivalent (see also [6,16]).

Equation (2.23) also has some important consequences.

• — The far-zone scattered field is circularly polarized. 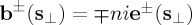(cf. equations (2.2)). This circular polarization holds with respect to the Cartesian system of orthogonal axes defined by the unit vectors: (ϵ_⊥,ϵ_∥,s) (figure 1). ϵ_⊥ and ϵ_∥ being respectively perpendicular and parallel to the polar plane (which now becomes the scattering plane) delimited by s and its projection on OXY ; i.e. 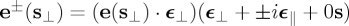and .

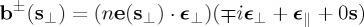From the above it should also be noticed that it is the handness of the dipole moments, and not necessarily the chirality α_me, the relevant characteristic for these CD effects. Besides, this CPL property of the scattered field is just a consequence of the optical theorems of energy and helicity, and does not presupose in the particle neither chirality, α_em=−α_me, nor duality, ϵ⁻¹α_e=μα_m [16]. Although the combination of both theorems imposes [16] that the existence of one these two last properties of the particle polarizabilities implies the other.

• — In the near field zone, the scattered wave in the basis (ϵ_⊥,ϵ_∥,s) has

  2.24

Thus, this field being CPL at points r along the polar axis OZ (θ=0, or θ=π).

3. Excitation of helicity and energy with general optical fields: the role of angular spectra with right-circular and left-circular polarization

Returning to equations (2.6)–(2.10) for general optical fields, we have from the optical theorem for the helicity (1.2) the following expression for its extinction from the incident field on scattering by the particle-induced dipole:

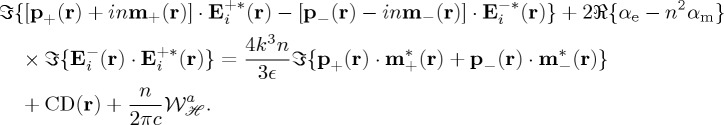3.1

While the extinction of incident energy is according to the standard optical theorem (1.3)

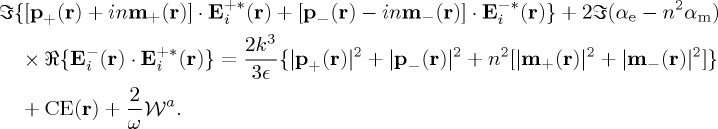3.2

The terms CD(r) and CE(r) are

3.3

and

3.4

In these equations, r denotes the position vector of the centre of the particle immersed in the illuminating field. Now, in contrast with the scattering of an incident elliptically polarized plane wave discussed above, the scattered helicity and energy convey interference between 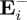and .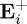

Note that by virtue of the asymptotic expression (2.13), in the far-zone 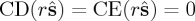as 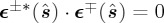. It is also interesting to observe from (3.1)–(3.4) that if the particle is dual, α_e=n²α_m, the terms of interference between E⁺ and E⁻ are zero and so are CD(r) and CE(r) for any r. Then (3.1) and (3.2) reduce to equations similar to (2.16) and (2.17).

However, the important point is that now the appearance of the interference factor 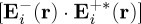in (3.1) and (3.2) allows one to choose the incident field such that eithe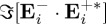r or 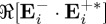is zero, or small, for the extinction rates of helicity (3.1) and of intensity (3.2), respectively. We thus shall analyse the consequences of 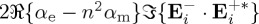or 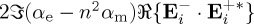being non-zero in the left sides of (3.1) and (3.2), respectively, as a consequence of the choice of illumination on the particle.

Using (2.9) the left sides of (3.1) and (3.2) are in terms of the polarizabilities and fields

3.5

By means of (3.5) we now address the rate of extinction of helicity 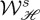(cf. equation (17) in [16]) and energy 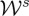in the particle, given by the left sides of (3.1) and (3.2), as functions of the polarizabilities

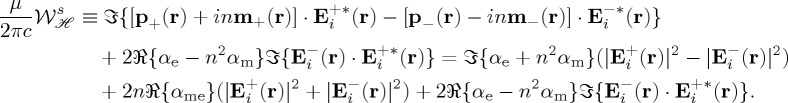3.6

and

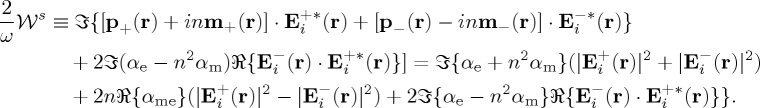3.7

Note that 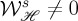even if α_me=0 and . It should be remarked that in the particular case of incident CPL plane waves, or CPL beams without longitudinal component, one has (choosing propagation along e.g. OZ): 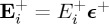, 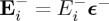; and as 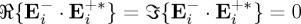, equation (3.1) becomes (2.16) and equation (3.2) reduces to (2.17). Hence, in this case 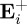and 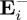do not interfere, and when 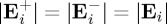equations (3.6) and (3.7) are similar to those of standard circular dichroism which our formulation shows that yields the rate of helicity extinction, first with an incident LCP wave, and then with one being RCP, both of the same amplitude. In such a situation, (3.6) and (3.7) become respectively proportional to the well-known numerator, 4nα^R_me|E_i(r)|² and denominator, of the CD dissymmetry factor [4,23]. (The superscripts R and I denoting real and imaginary part.)

However, our general equations (3.6) and (3.7) cover many other configurations (in particular those so-called superchiral fields [4], which is known, however, to be limited to molecules with α_m≃0 [23]). We next show the broader scope of (3.6) and (3.7) with chiral optical beams possessing a longitudinal component, which as we shall show, plays a key role. We will see that according to whether one chooses such illuminating beams yielding eithe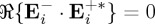r or 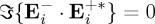one respectively enhances the extinction rate of helicity (3.6) versus that of energy (3.7) (and thus the ratio between them) or vice versa. Note that because out of resonance the real part of the polarizabilities are usually greater than the imaginary parts, the last term of (3.6) may be larger than that of (3.7). Hence, one may produce bigger enhancement in 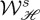than in 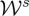with those choices of ℜ and ℑ of .

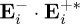4. Optical beams whose angular spectrum representation contains left-circular and right-circular plane waves

In the paraxial approximation ∂_z≃ik_z, so that the equation ∇⋅E=0 implies that E_z=(i/k)∇_⊥⋅E_⊥ [35]; (⊥ denotes transversal, i.e. XY component). The electric vector of an optical beam is then written in terms of its angular spectrum as [32,33]

4.1

Having denoted r=(R,z), R=(x,y,0), s=(s_⊥,s_z), s_⊥=(s_x,s_y,0).

We shall consider the Gaussian beam, i.e. the one from which other fields, like Hermite and Laguerre–Gaussian beams, are generated [36].

We write for (4.1) the decomposition (2.3) of each component into LCP and RCP waves by expressing the Gaussian angular spectrum [32,33] as 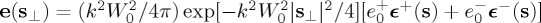. 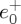and 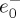being complex constants, and W₀ standing for the beam waist at z=0. Then, we express the beam as

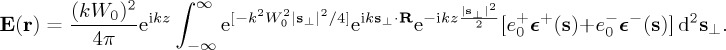4.2

Recalling that 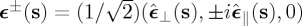, and writing in the Cartesian basis 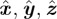(figure 1): 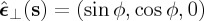, , 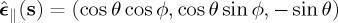, 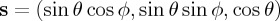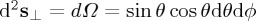. 0≤θ≤π, 0≤ϕ≤2π.

Performing the ϕ and θ integrals we obtain (see integrals 3.937.2 and 6.631.1 of [37]) after making 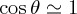in all factors of the integrand but not in the exponentials as involved in the paraxial approximation, and writing 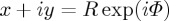, Φ being the azimuthal angle, we derive

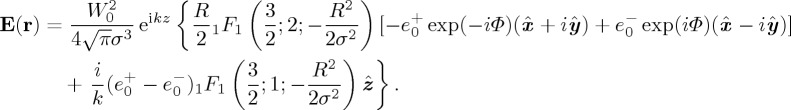4.3

₁F₁ is Kummer’s confluent hypergeometric function [38]. 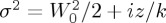. Equation (4.3) represents a hypergeometric beam which, containing LCP and RCP plane waves, differs from some previously put forward [39]. A generalization of this beam to arbitrary index m with vortices 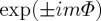and topological charge m is made by including a factor 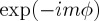in e(s_⊥). Note from (4.3) that due to the paraxial approximation the transversal XY -component of E is the sum of two fields (cf. equation (2.7)): one, E⁺, is LCP and has a complex amplitude proportional to 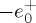; the other, E⁻, is RCP and its amplitude factors 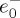. 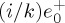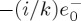These two CPL beams also have a longitudinal component E_z, proportional to and , respectively, as shown by the last term of (4.3). Next, we see the relevance of this longitudinal component to control the dipole emission, enhancing either the emitted helicity or energy. Using (4.3), we obtain for the incident energy and helicity factors in the left side of (3.6) and (3.7) (we now drop the subindex i in those equations, understanding that the incident electric field is (4.3))

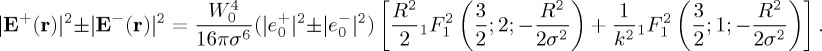4.4

Of course the choice of the upper or lower sign in ± of (4.4) yields the beam energy or the helicity (cf. equation (2.12)), respectively.

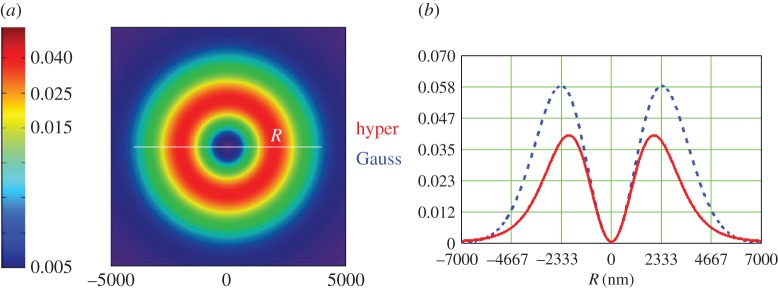
Figure 2 shows the transversal intensity distribution |E⁺|²+|E⁻|² of this beam, given by equation (4.4) at z=0, for 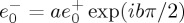, b real, 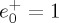(in arbitrary units) a=1 , λ=589 nm, W₀=4λ. This choice of the value of 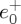and the presence of the factor 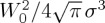of the beam amplitude in (4.2) produces small values of these intensities. Also as R²≫λ², apart from points close to R=0 the second term of (4.4), given by the longitudinal component of the beam, hardly contributes to this intensity distribution. However as seen next, this longitudinal component becomes crucial when the helicity, extinguished from the incident beam and thus radiated or scattered by the particle is considered. For comparison, we also show this intensity distribution when the ₁F₁ functions of (4.4) are substituted by a Gaussian with the same value of σ². The difference between both distributions is small due to the similar shapes of the Gaussian and these hypergeometric functions. On the other hand, the real (and imaginary) part of the product E⁻⋅E⁺ reduces to

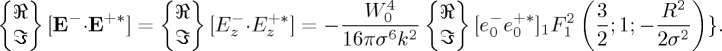4.5

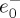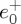So that either of these quantities, ℜ[⋅] or ℑ[⋅], may be made arbitrarily small (or zero) depending on the choice of parameters and for the beam, which may make arbitrarily small (or zero) the factor 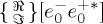. In the next section, we show the relevance of this choice in connection with equations (3.6) and (3.7). For example, choosing as for figure 2 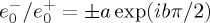, a and b being real, the value of 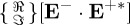will oscillate as 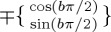, thus possessing several zero values in the interval 0≤b≤4.

Figure 2.

Intensity |E⁺|²+|E⁻|² (cf. equation (4.4)) at z=0 of the hypergeometric beam of equation (4.3) . (a) Colour map of the transversal distribution. (b) A cut of this spatial distribution as a function of the coordinate R along a diameter (full red).The distribution when the ₁F₁ functions are replaced by a Gaussian of the same σ is also shown (broken blue line). (Online version in colour.)

Note that a kind of Hermite and Laguerre–Gaussian beam modes (m,n) are straightforwardly worked out from (4.3) on making upon E(r) the operations 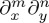and (∂_x+i∂_y)^m(∂_x−i∂_y)^m+n, respectively [36]. Likewise, Bessel beams with LCP and RCP angular components may be described by equation (4.2) using an angular spectrum .

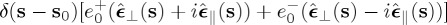5. Example: enhancing the extinction of either chirality or energy

As an illustration of the relevance of equations (3.6) and (3.7), we consider a helical molecule with α^R_e=1.04×10⁻² nm³, α^I_me=6.2×10⁻⁵ nm³, α^R_me=0, in an environment with ϵ=μ=1 at an illumination wavelength λ=589 nm. 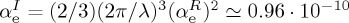nm³≪α^R_e, |α_m|<10⁻⁵|α_e| [19,40].

These polarizabilities yield according to (3.6) and (3.7) for the helicity extinction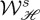

5.1

and for the total emitted energy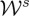

5.2

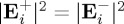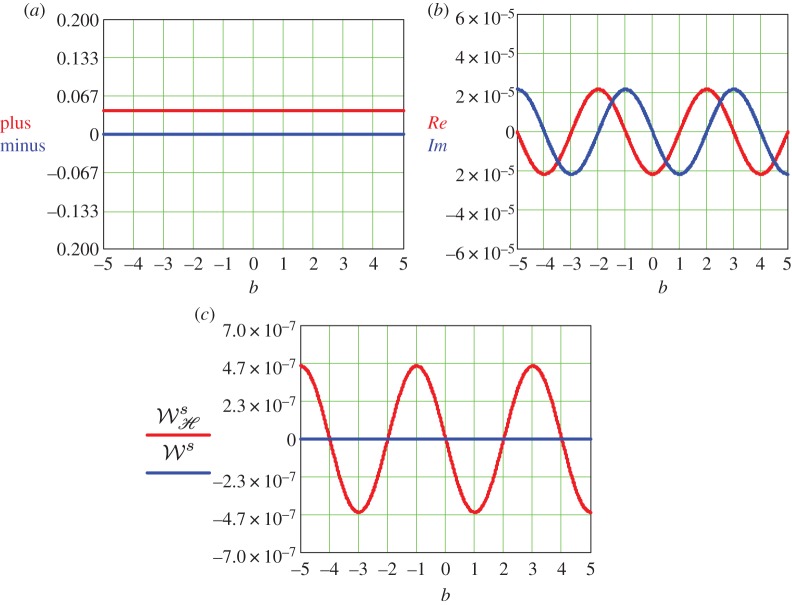
We see from (5.1) that objects with such a purely imaginary α_me would produce no signal in a standard circular dichroism configuration, i.e. under illumination with plane CPL waves, for which , E⁻⋅E^+*=0. (We recall that in such experiments the objects (molecules) usually have α^R_me≤10⁻³α^I_e, but α^R_me≠0.) However, impinging the particle by LCP and RCP beams with longitudinal component, like those of equation (4.3), and for example choosing as above 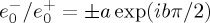, figure 3 shows, at R=2000 nm and z=0, 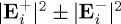, as well as ℜ (and ℑ) of [E⁻⋅E^+*] as functions of b for W₀=4λ, a=1. The incident helicity, given by the quantity minus of figure 3, is zero as 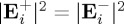. As seen, the oscillations of the term 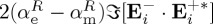of (5.1) and of 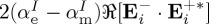of (5.2) lead to those of the helicity 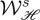and energy 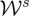extinction rates, respectively. The latter is constantly zero due to the very small value of the factor 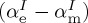for these polarizabilities.

Figure 3.

(a) Intensity, plus = |E⁺|² + |E⁻|² (red line), and helicity, minus = |E⁺|² − |E⁻|² (blue line) (cf. equation (4.4)), as a function of b for the hypergeometric beam of equation (4.3) at z=0 and near the peak at R=2000 nm (figure 2b). 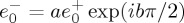, 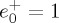(in arbitrary units), a=1. (b) Re=ℜ[E⁻⋅E^+*] and Im=ℑ[E⁻⋅ E^+*](cf. equation (4.5)), for the same beam and choice of parameters. (c) Extinction rate of helicity 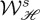(full red) and energy 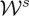(broken blue) in terms of b. (Online version in colour.)

The corresponding quotient between 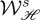and 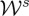would be very large in this case. Therefore, this is just an illustration of how such a ratio may be enhanced depending on the constitutive parameters of the particle and choice of the beam. Other objects with different values of the polarizabilities may yield similar enhancements of either the emitted helicity—chirality—or energy depending on whether ℑ[E⁻⋅E^+*] dominates upon ℜ[E⁻⋅E^+*] in (3.6) and (3.7), or vice versa. For instance, were the ‘particle’ magnetodielectric with α^I_m comparable to α^R_e, or just one or two orders of magnitude smaller (a difficult case to deal with conventional circular dichroism [23]), the factor 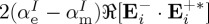will give rise to an amplitude of the oscillations in 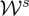comparable to that in 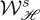, or one or two orders of magnitude lower. However, the phase shift of the oscillations of 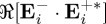and 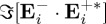(cf. Re and Im in figure 3) allows us to tailor the beam, producing an enhancement 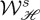of or of .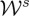

6. Concluding remarks

Based on a recent optical theorem put forward for the electromagnetic helicity, or chirality, extinction rate of quasi-monochromatic wavefields [16], which characterizes the emitted or scattered helicity by extinction of that of the incident field, we have demonstrated that dichroism is not only a manifestation of molecular absorption, but it is a universal phenomenon which appears in the scattering or diffraction of twisted waves. This provides a general basic answer to the question on the conditions under which an object produces chiral fields and/or dichroism, and whether a chiral scatterer is required to produce such effect.

In this respect, we have established that both dichroism and chirality of emitted or scattered wavefields from wide sense dipolar particles are consequences of the helicity of the illumination, or of the mutual relationship between the emitting electric and magnetic dipoles; but these phenomena do not require the object constitutive parameters, refractive indices and polarizabilities, to be those of a chiral structure. For example, as we have shown, to obtain a circularly polarized emitted or scattered field, it is a sufficient condition that the particle-induced electric and magnetic dipoles rotate and differ from each other by only a ±π/2 phase; but no chiral cross-polarizability α_me is necessary. Thus, an achiral particle (α_me=0) may produce dichroism on scattering of a chiral incident wave. Henceforth, the standard concept of circular dichroism is generalized to include fields with both LCP and RCP components and a net helicity.

Based on the angular spectrum representation, we have introduced new families of optical beams with right-circular and left-circular polarization, and with longitudinal components. Tailoring these fields, used in our optical theorem as incident waves on the scattering particle, overcomes previous limitations of circular dichroism without needing to place nearby additional objects to enhance the signal [29,30,41]. Depending on the parameters chosen for these beams, the enhancement of the extinction rate of helicity and/or of energy is produced, i.e. the dichroism scattered signal is either augmented or lowered. This not only provides a new procedure for object (and particularly enantiomeric) characterization on illumination with twisted beams, but it also yields a way of controlling the helicity and energy of radiated wavefields by using such scattering particles as secondary sources.

Competing interests

I declare I have no competing interests.

Funding

Work supported by MINECO, grant nos. FIS2012-36113-C03-03, FIS2014-55563-REDC and FIS2015-69295-C3-1-P.