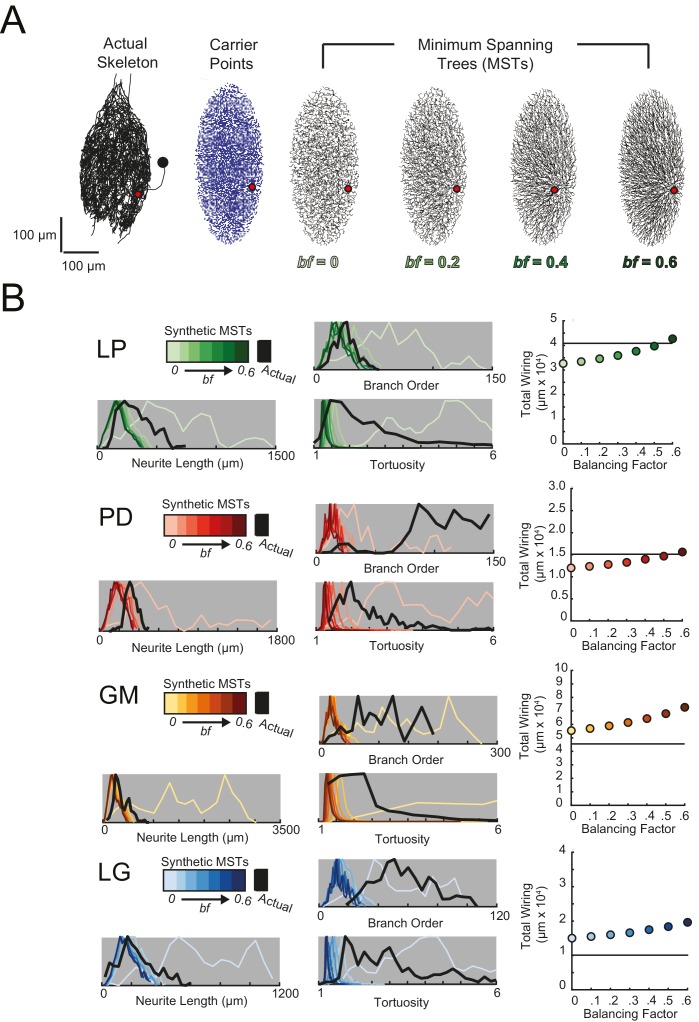
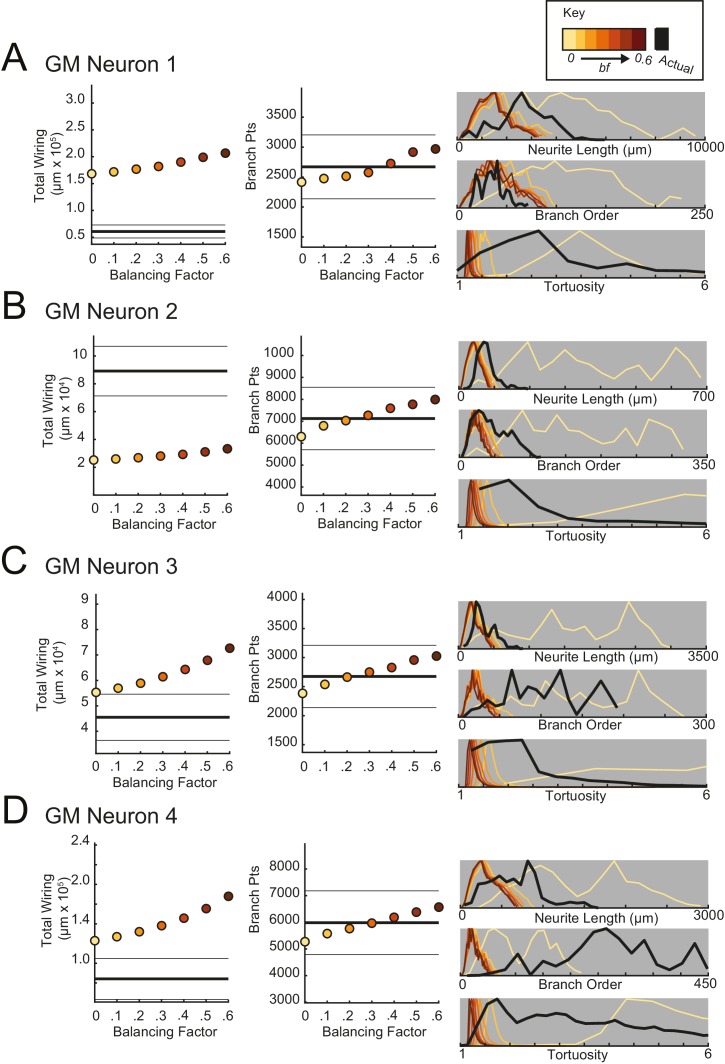
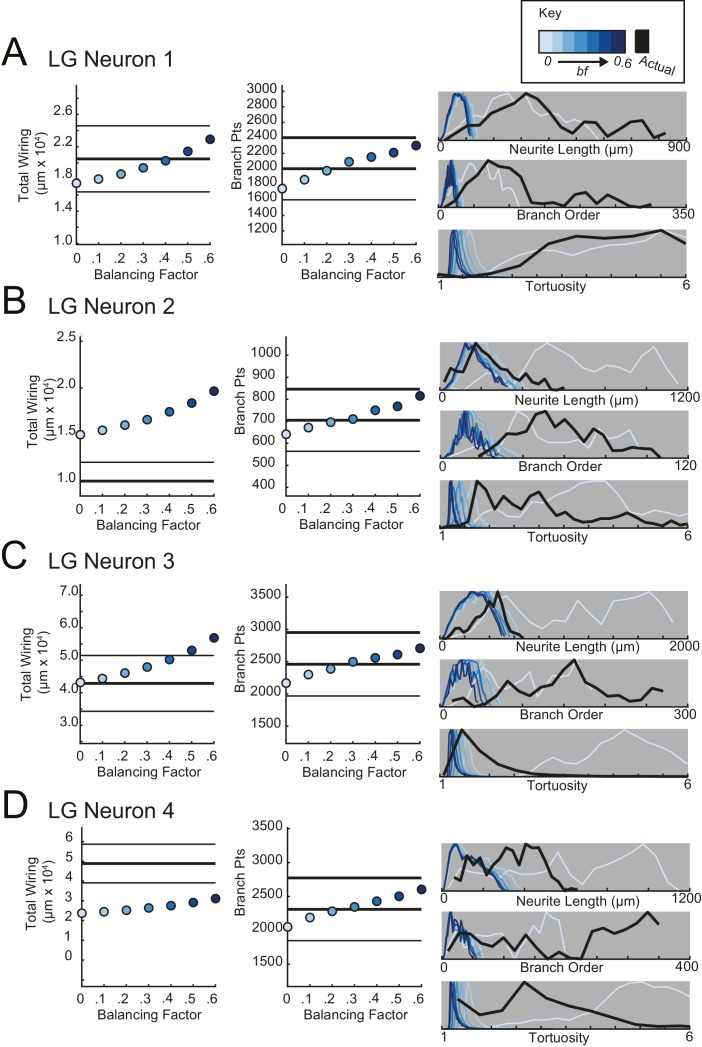
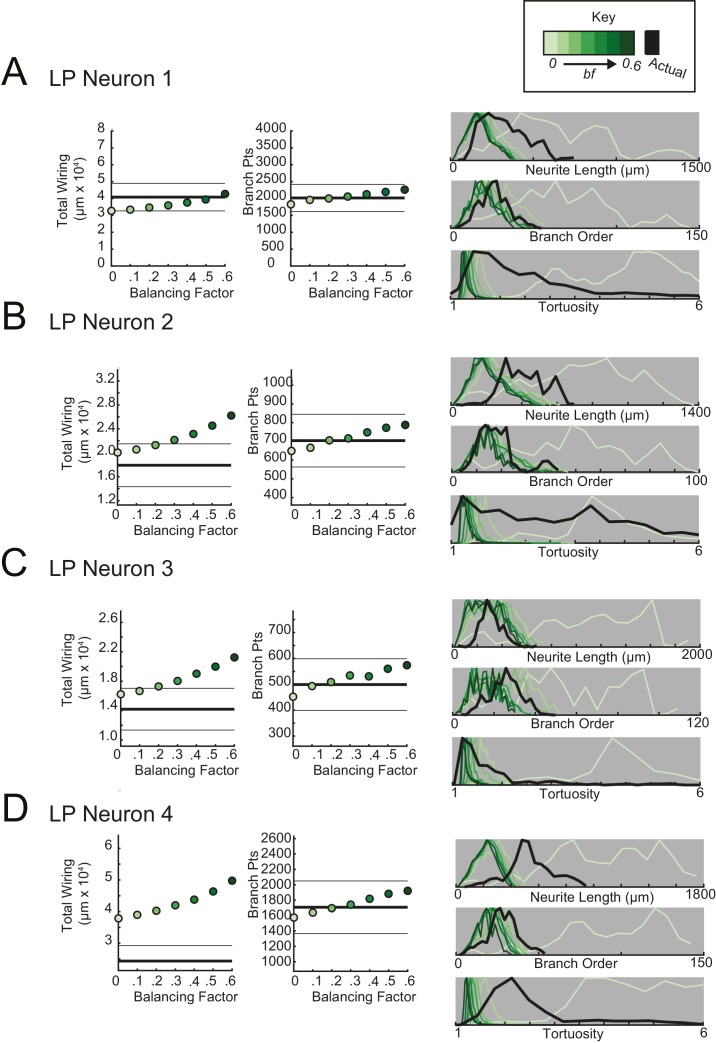
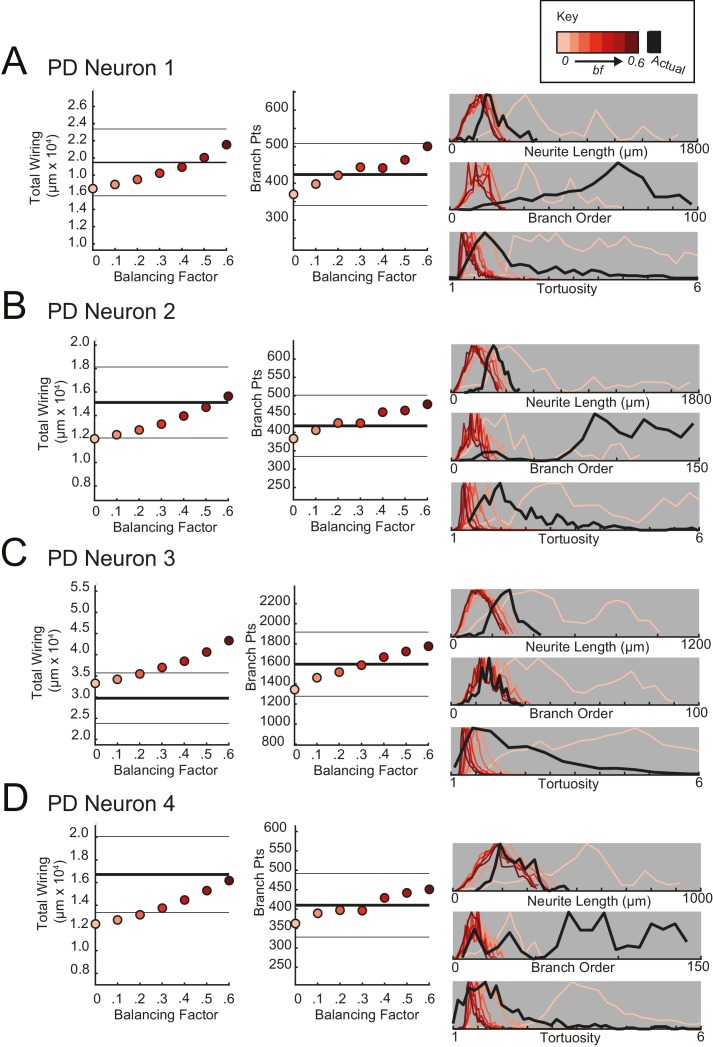
Figure 11. Minimal Spanning Trees (MSTs) adhering to wiring optimization rules do not recapitulate the morphological features of individual STG neurons.
Synthetic MSTs adhering to the wiring cost rule: total cost = wiring cost + bf * path length cost (where bf = balancing factor) were generated using the TREEs toolbox (described in Materials and methods and by Cuntz et al., 2010). (A) An example of four synthetic minimal spanning trees (right) with varying bf values generated from the first branch point (location indicated as red circle on actual skeleton of an LP neuron; left) as the root. The carrier points (blue) were randomly generated from points uniformly distributed across the elliptical volume approximating the actual volume occupied by the neuron. The number of carrier points was tuned such that the MSTs had branch point number within 20% of the actual neuron’s branch point number (Table 3). Scale bars apply to skeleton, carrier point, and MST plots. (B) Morphological features of synthetic trees generated with bf values between 0.1 and 0.6 plotted against measurements from four actual STG neurons (one of each type, indicated on left and by color). Features of actual neurons are shown with black lines, whereas synthetic neurite tree data are plotted in the color scale described in the key for each neuron. Total wiring lengths, branch order distributions, neurite length distributions, and tortuosity distributions were calculated excluding axons for all synthetic and actual neurite trees. Branch order, neurite length, and tortuosity distributions were normalized to the maximum within each data set (for each bf value and actual neurite tree) for direct comparison of distributions despite varying neurite path counts.