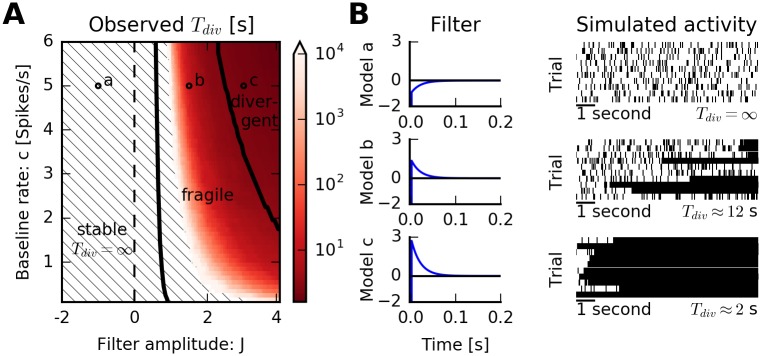
Fig 5. Predicted stability reflects simulation outcomes: Exponential spike-history filter.

(A) Spike trains are simulated from a nonlinear Hawkes model with baseline firing rate c and an auto-history kernel η(s) = J exp(−s/τ) with amplitude J, time constant τ = 0.02 s, and absolute refractory period τ_ref = 2 ms. The QR approximation qualitatively predicts three classes of dynamics (separated by thick lines). Color indicates average divergence times estimated from simulations. In the dashed region, no finite divergence times were observed. (B) An example of a spike-history filter for each of the dynamics is shown together with a spike raster of simulated activity. Purely inhibitory filters produce stable dynamics (top, J = −1, c = 5 s⁻¹). For fragile models, after an episode of irregular firing, dynamics switches into a tonic firing mode close to the limit frequency 1/τ_ref (middle, J = 1, c = 5 s⁻¹). For divergent models, the only stable fixed point is close to the limit frequency (bottom, J = 3, c = 5 s⁻¹). After a brief transient, the model switches to the tonic firing mode at limit frequency. All dynamics observed in simulations are in accordance with the prediction from the QR approximation.