Bridging, brokerage and betweenness

Abstract

Valente and Fujimoto (2010) proposed a measure of brokerage in networks based on Granovetter’s classic work on the strength of weak ties. Their paper identified the need for finding node-based measures of brokerage that consider the entire network structure, not just a node’s local environment. The measures they propose, aggregating the average change in cohesion for a node’s links, has several limitations. In this paper we review their method and show how the idea can be modified by using betweenness centrality as an underpinning concept. We explore the properties of the new method and provide point, normalized, and network level variations. This new approach has two advantages, first it provides a more robust means to normalize the measure to control for network size, and second, the modified measure is computationally less demanding making it applicable to larger networks.

1. Introduction

The ideas of bridging and brokerage have a long tradition in social network analysis. Granovetter’s (1973) classic paper on the strength of weak ties and the work that followed by various authors demonstrated that being in a position of control over bridging ties can empower actors. Burt (1995, 2007) further developed these ideas using ego network measures in his books on structural holes and brokerage and closure. Gould and Fernandez (1989) also took an ego approach in their classification of brokerage roles on data with categorical attributes. Shetty and Adibi (2005) develop entropy-based measures of edges which are then aggregated for each node to provide node level measures of importance. Valente and Fujimoto (2010) introduce a brokerage measure for nodes based upon an edge cohesion measure. A similar idea had in 2009 been implemented in UCINET (Borgatti et al., 2002). The k-local bridges routine (Granovetter, 1973) was extended to include node level statistical summaries and these can be viewed as a measure of brokerage. In all of these papers the underlying assumption is that actors control resources which are flowing through the ties that they are incident to. Bridging is an edge property that measures the extent to which an edge forms a bridge. Brokerage is defined as control over bridging and is a node level property. By control over bridging we mean that a node’s brokerage is a function of the bridging scores of the edges it is incident to.

In their paper Valente and Fujimoto (2010) propose a measure that indicates the degree to which a node occupies a brokerage position in a network. In their method they systematically delete each edge in the graph and calculate the change in the amount of cohesion in the network, where cohesion is the average reciprocal distance between all pairs of vertices. This gives a value for each edge and the average of the edges incident to each vertex gives the brokerage score for that vertex. Their rationale for taking the average is that each edge requires resources to maintain it and so high degree nodes should be penalized for having many ties. We shall refer to their measure of brokerage as VF-brokerage or simply VF. (Note they call their measure a bridging measure but we prefer the term brokerage as it is more consistent with the literature.) This process is very similar to both the UCINET k-local bridge and the algorithm described by Shetty and Adibi (2005).

We summarize the process as follows.

1. Systematically delete each edge in the network.

2. Once an edge is deleted measure the effect of the deletion on a network metric by calculating how much it has changed and assign this value to the edge.

3. For each vertex assign a brokerage score which is the average of the edge values incident to it.

Step 2 for k-local bridges assigns edges the distance between the nodes it previously connected and for the VF measure step 2 assigns the change in the average reciprocal distance between all pairs of vertices. The Shetty and Adibi (2005) approach is similar but cannot be specified in the same way using this process.

One limitation with the k-bridge measure is that it only considers the change in distance between the end points of the bridge and does not look at the effect of deletion on the whole network. As a consequence in some circumstances the measure is very insensitive to network structure. If we look at the case in which the deleted edge is a graph theoretic bridge (an edge whose removal increases the number of components), then we can see the measure does not distinguish between bridges that bridge two large components, as opposed to a bridge that connects a singleton to the rest of the network. As an extreme example, in a tree every node would get the same brokerage score regardless of its structural position. The VF-brokerage does not suffer from this problem and will take account of the position of the bridges in the network.

There are however three issues with the VF measure that we propose to address. First, Valente and Fujimoto argue that pendant vertices should be given a score of zero arguing: “Conceptually, bridging nodes cannot be nodes linked to only one other node. The one link these nodes have does not influence distances between other nodes” (p. 215). The argument they make is that the pendant nodes do not bridge anything as they do not lie on any shortest paths where they are not endpoints. This is of course true and we understand the reason for this argument, however, this categorizes pendants the same as isolates. Although pendants have less brokerage potential than nodes that are within a shortest path, they may have some resource which they can use by virtue of the one connection they have. Clearly this will depend on the data and application area and is not a serious issue or criticism of their measure; but does require a trivial change if an analyst felt this was not valid for their situation.

A second, and more serious concern, of the VF approach is that they only apply this reasoning to pendant vertices and not any vertex with that property. There could be vertices of higher degree that have no brokerage potential. That is, they are not on any shortest path except as an endpoint, but are not also set to zero. Such vertices would have a vertex betweenness score of zero and are quite common in many networks. This occurs when the induced neighborhood of a vertex is a complete graph (see vertex 12 in Fig. 1 for an example). For pendant vertices this neighborhood is simply the complete graph K₂ (here we used closed neighborhoods, those that include ego, the same holds if we use open neighborhoods, those with ego removed, in this case the graph would be K₁).

Fig. 1.

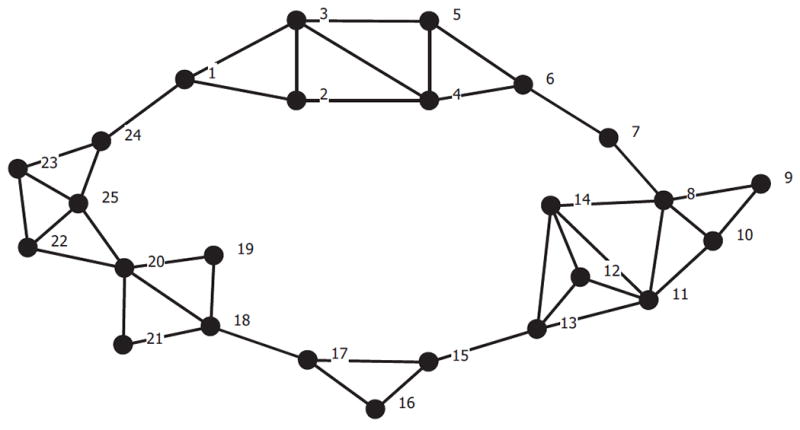
Granovetter’s hypothetical network reported in the strength of weak ties article.

A third issue is with the way they normalize their measure. A point we shall return to later.

2. A simplified brokerage measure

As already discussed by Valente and Fujimoto the measure they discuss is actually an edge centrality computed by examining its influence on a graph invariant measure when the edge is deleted. Both Koschützki et al. (2005) and Everett and Borgatti (2010) discuss this general method for defining edge centralities but the concept is much older; for a review see Koschützki et al. (2005). The original term for these was vitality measures but Everett and Borgatti (2010) suggested naming them induced centrality measures.

Rather than using an induced centrality, that is edge deletion, to obtain edge centralities, another approach is to use a standard edge centrality measure such as edge betweenness (Anthonisse, 1971). Edge betweenness has been well researched and can be calculated with standard algorithms available in most network analysis platforms. In addition edge betweenness is defined exactly the same for directed as well as undirected networks and so naturally extends to the directed case. Finally edge betweenness is a measure which takes account of the sizes of the node sets the edge is between. We therefore propose a two stage process as follows:

1. Calculate an edge centrality measure.

2. For each vertex assign a brokerage score which is the average of the edge centralities which are incident to it.

Clearly this is the same as the process discussed in the introduction, as in that case the edge centralities were given by induced centrality methods for edges. We suggest here that we use edge betweenness as the centrality measure. There is one real advantage in using edge betweenness as a consequence of the following theorem which is an extension of a result due to Koschutzki et al. (2005, p. 31).

Theorem 1

In a directed graph with n vertices the betweenness of a vertex v is the sum of the edge betweenness scores of the out-going (or in-coming) ties minus k, where k is the number of vertices that v can reach (or can reach v).

Proof

Koschützki et al. (2005) prove the result for strongly connected graphs (in which case k = n − 1) and it is a simple matter to extend their proof to the case when the graph is not strongly connected so that k < n − 1.

In an undirected connected graph the result is similar but this time we need to halve the sum of the betweenness scores before subtracting n − 1. This is a consequence of the way vertex betweenness was defined for undirected graphs as opposed to directed graphs. For undirected graphs we look at all shortest paths between pairs of vertices i and j where i < j. For directed graphs we look at all pairs.

We can now use this result to calculate brokerage in a similar way to Valente and Fujimoto (2010) using any software package that calculates standard node betweenness. Let t_jk denote the total number of shortest paths in an undirected graph G connecting vertex j to vertex k and t_jik be the number of shortest paths connecting j to k that pass through vertex i then the standard node betweenness of i, C_B(i) is given by:

$$C_B(i)=\sum _{j=k}\left(\frac{t_{\mathit{jik}}}{t_{\mathit{jk}}}\right)$$ (1)

The property of pendants being set to zero is retained here for direct comparison with VF. For undirected networks this leads to the following method.

1. Calculate standard vertex betweenness as given in (Eq. (1).

2. Double each score and add n − 1 to every non-pendant entry.

3. Divide each non-zero score by the degree of the relevant vertex.

The correlations between this new measure and the VF-brokerage one using the examples given in the VF paper range from 0.77 to 1.0. Regardless of the correlation, both methods tend to identify the same nodes as having highest brokerage scores. The higher correlations are for the toy example networks in Fig. 3 in the Valente and Fujimoto paper. The lower correlations are for the Kirke (2004) network of adolescents, 0.765, and for the network provided in Granovetter’s (1973) original strength of weak ties article (Fig. 4 in their paper) shown here in Fig. 1.

Fig. 3.

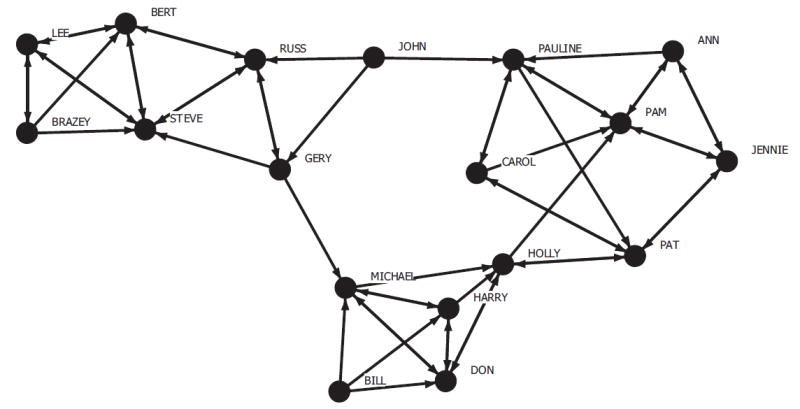
The campnet dataset.

Their original un-normalized brokerage scores labeled “Link Deletion (VF-brokerage)” and those derived from the method described above labeled “Edge Betweenness Divided by Degree” are given in Table 1.

Table 1.

Link deletion brokerage scores compared to betweenness brokerage scores all given as a percentage.

ID	Link deletion (VF-brokerage)	Edge betweenness divided by degree	Normalized EV-brokerage
1	1.3	46.511	29.814
2	0.3	17.668	11.325
3	0.3	23.044	14.771
4	0.3	23.286	14.926
5	0.3	17.768	11.389
6	1.2	47.527	30.465
7	3.0	72.09	46.21
8	0.9	33.956	21.766
9	0.3	12	0
10	0.3	10.667	6.837
11	0.3	20.498	13.139
12	0.2	8	0
13	1.2	43.117	27.638
14	0.3	17.923	11.488
15	1.6	56.606	36.285
16	0.4	12	0
17	1.6	56.184	36.014
18	1.3	42.605	27.31
19	0.4	12	0
20	0.6	32.964	21.13
21	0.4	12	0
22	0.3	11.8	7.564
23	0.2	10.667	6.837
24	1.4	46.273	29.661
25	0.5	31.955	20.483

We see that both measures place all 10 cutpoints (namely 1, 6, 7, 8, 13, 15, 17, 18, 20, 24) in the first 10 places but the rank ordering is slightly different. However the real issue is not the minor differences between the cutpoint rankings but the way some non-brokerage nodes acquire higher scores in the VF measure than in the betweenness based measure. Three of the five nodes that have betweenness scores of zero, 16, 19 and 21, are ranked in the middle for VF, yet fall in the last six scores for the new measure. For example, actor 16 is ranked 12th out of 25 in VF whereas it is tied with nodes 19 and 21 in the 19th through 21st ranking in the revised brokerage.

We suggested above that if the application area implies that actors only acquire brokerage by connecting pairs of actors that do not include themselves then we should set all actors with this property a value of zero, and not just the pendants. In this case the following would be a more appropriate brokerage measure for the undirected case.

EV Brokerage for undirected graphs

For each component of size n.

1. Calculate standard vertex betweeneess.

2. Double each score and add n − 1 to every non-zero entry.

3. Divide each non-zero score by vertex degree.

We shall call this measure EV-brokerage. If the analyst feels that actors can acquire brokerage from themselves to their neighbors then step 2 becomes simply add n − 1 to every vertex and this is then the same as using edge betweenness throughout. Implementing these steps on the Granovetter data yields exactly the same as in column 2 in Table 1 except vertices 9, 12, 16, 19 and 21 will have values set to zero.

3. Normalization

Valente and Fujimoto (2010) claim that the measure they introduce is at a maximum for a star and they use this value to normalize their measure and they imply the following conjecture.

Conjecture. Let v_max be a vertex with the maximum VF-brokerage over all graphs G with n vertices. Then the VF-brokerage score of v_max is given by 1/(n − 1).

Actually they state the value is 1/(2n − 2) for a star but they have an error in their calculation and it should be as given in the conjecture. Nevertheless this conjecture is false. As a counter example consider two copies of the complete graph K₄ connected by a path of length 2 with v as the vertex of degree 2 on the path (Fig. 2). The resultant graph has 9 vertices and v has a VF-brokerage score of 0.132 whereas the conjecture states the maximum should be 0.125.

Fig. 2.

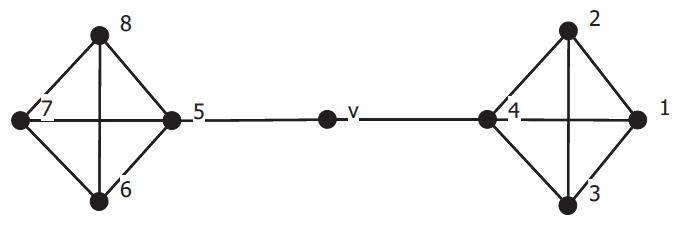
A maximally bridgeable network with v having the highest brokerage score.

While it is true that the highest change in the average reciprocal distance occurs when the edges of a star are removed; dividing by the degree of the vertex to obtain their score counteracts the high values obtained. We conjecture that maximal VF-brokerage occurs when a vertex connects two vertices of two otherwise unconnected cliques of equal size by a path of length two. However we do not explore this further here but as a consequence anyone applying VF-brokerage should not use the formula they propose for normalization, but use the point scores.

The following theorem, which uses a similar structure but relaxes the clique condition, allows us to normalize the EV-brokerage measure. To prove this result we first require the following lemma proved in Everett et al. (2004).

Lemma

If a vertex u is neither a pendant or cutpoint of a graph G then there exists a subgraph K of G such that the betweeness of u in K is greater than the betweenness of u in G.

Theorem 2

Let v_max be a vertex with the maximum EV-brokerage over all graphs G with n vertices, where n > 2. Then the EV-brokerage score of v_max is given by

$$\begin{array}{c}{v}_{\max }=(n^2-1)/4\mathrm{if\; n\; is\; odd}\\ v_{\max }=(n^2-2)/4\mathrm{if\; n\; is\; even}\end{array}$$ (2)

Proof

We shall give a slightly simplified proof for the sake of clarity but the argument can be made rigorous.

Since n is larger than 2 then clearly v_max will not be a pendant vertex. By the lemma v_max must be a cutpoint since if it were not there would be a subgraph K in which v_max would have higher betweenness and, as it is a subgraph, the same or lower degree and hence a strictly higher EV-brokerage score. Let H be the component of G containing v_max. Suppose G is not connected then connecting any component of G different from H with a component of H − v_max will result in a graph in which the EV-brokerage score must increase, since the betweenness of v_max must increase and its degree will be unaffected. It follows that G is connected.

Let the components of G − v_max be B₁, B₂, …, B_k. The betweenness centrality of v_max will be highest when the order of each of these components differs by at most one. It follows that each component has order (n − 1)/k with some rounded down and the rest rounded up. Since geodesics in G with endpoints in different B_i must pass through v_max then each pair of Bi’s contributes ((n − 1)/k)² to the betweenness of v_max. As there are k blocks it follows that there are k(k − 1)/2 pairs of blocks so that the betweenness of v_max is approximately given by

$$\frac{1}{2}k(k-1){\left(\frac{n-1}{k}\right)}^2$$ (3)

The EV-brokerage of v_max is now obtained by the construction described above, that is, doubling this value, adding n − 1, and dividing the total by the degree of v_max(=k). This yields a value for EV-brokerage of v_max approximately given by

$$\frac{k(k-1){(n-1)}^2+k^2(n-1)}{k^3}$$ (4)

where k is vertex degree of v_max and n is the network size. As k increases this value decreases for fixed n as it is dominated by the denominator. It follows EV-brokerage is at a maximum when k has the minimum value of 2. If n is odd then formula 2 is exact and the result follows by substituting k = 2. If n is even then G − v_max will have two components one of size n/2 and the other of size (n − 2)/2. It follows that the betweenness of v_max is n(n − 2)/4 and so the EV-brokerage is n(n − 2)/4 + (n − 1)/2 which reduces to (n² − 2)/4.

We note that if n = 1 or 2 then any EV-brokerage cannot be non-zero.

It should be noted that the theorem carries over with minor changes for the directed graph case and the same result holds. If we apply the normalization to Fig. 1 then we obtain the normalized EV-brokerage scores reported in the final column of Table 1.

It can be seen from the proof of the theorem that the overall structure of the graph on which the maximum score is obtained is not important. The only property we require is that the vertices are evenly distributed either side of the cutpoint v_max. They can have any structure and so there are a large number of configurations which give the same maximum value. The only limitation would be on the number of edges in each component and this implies the graph can have at most (n² − 4n + 11)/4 edges for n odd and (n² − 4n + 12)/4 for n even.

4. Aggregate brokerage and brokerization

Freeman (1979) introduced the idea of centralization, which measures the extent to which centrality is focused on one or a few nodes in the network. We can apply a similar idea to our brokerage measure which we call brokerization. For Freeman a star graph provided the structure in which the central vertex had all the centrality and all other vertices had the minimum centrality over all connected graphs. For the EV-brokerage we simply require that the graph described in the theorem above (Fig. 2) is one in which B₁ and B₂ are complete graphs to ensure that the EV-brokerage of nodes in B₁ and B₂ are minimized. In this case all vertices except those connected to v will have EV-brokerage scores of zero. A simple calculation will show that the values of the non-normalized EV-brokerage of the two vertices adjacent to v are: (n² − 5)/(n − 1) for n odd (for both vertices), and (n² − 2)/n and (n² − 10)(n − 2) when n is even (the first term for the larger of the two sets B₁ and B₂ and the second for the smaller).

If we now calculate the value of the brokerization on these extreme examples using non-normalized scores we obtain values for the denominator in any brokerization normalization and these are:

$$\begin{array}{c}\mathrm{For\; n\; odd}\\ \frac{(n^2-1)(n-1)}{4}-\frac{2(n^2-5)}{n-1}\end{array}$$ (5)

$$\begin{array}{c}\mathrm{For\; n\; even}\\ \frac{(n^2-1)(n-1)}{4}-\frac{2(n^3-2n^2-12n+4)}{n(n-2)}\end{array}$$ (6)

Applying this to the Granovetter example we obtain a value of 0.20 or 20%. This compares with just over 14% for betweenness centralization. Hence the brokerage is slightly more concentrated in one, or few, actor(s) than betweenness.

The aggregate brokerage in a network is simply the sum of all the brokerage scores of the vertices. The following theorem gives the maximum possible scores over all graphs but we first make use of a simple lemma. The lemma has been noted by others but has not been stated explicitly in print, it is a direct consequence of a result first noted by Freeman (1980) and more recently by Brandes et al. (2016). We give a simple direct proof.

Lemma 3

Let B(G) be the sum of the betweenness scores of every vertex in G. If x is an edge that is on a cycle then B(G − x) > B(G).

Proof

Since G − x is still connected then the lengths of some geodesics must strictly increase. Since each non-endpoint vertex on a geodesic acquires betweenness from the geodesic it follows that the total betweenness must increase.

Note this implies that the graph with the highest total betweenness must be a path as it is the tree with the longest possible geodesics.

Theorem 4

Let G be a graph on n vertices with the maximum possible aggregate non-normalized EV-brokerage. Then the aggregate non-normalized EV-brokerage of G is given by: For n odd

$$\left(\frac{n^2-1}{4}\right)\left(\frac{2n+3}{3}\right)-(n-1)\left(\frac{n+5}{4}\right)$$ (7)

$$\begin{array}{c}\mathit{For\; n\; even}\\ \frac{n(n+1)(n+2)}{6}-\frac{n^2+3n-2}{2}\end{array}$$ (8)

Proof

As already noted a path has the highest possible total betweenness. Since every non-pendant vertex has the lowest possible degree it follows that over all graphs of size n a path containing n vertices has the highest aggregate EV-brokerage.

As the proof for the odd and even case are similar we shall just prove the even case. The betweenness score for a vertex of distance k > 0 from the nearest endpoint of P_n is given by k(n − k − 1). It follows that the EV-brokerage score will be k(n − k − 1) + (n − 1)/2 for each of the non-end vertices. Hence the aggregate score will be

$$2\sum _{k=1}^{\frac{n}{2}-1}\left[k(n-k-1)+\frac{n-1}{2}\right]$$ (9)

Which after a small amount of manipulation reduces to the result in the theorem.

Again applying this to the Granovetter example we have that the sum of all the (non-normalized) EV-brokerage scores is 663 this is the sum of the values in column two of Table 1 but with 9, 12, 16, 19 and 21 set to zero. For n = 25 the above formula yields a maximum possible score of 2576 giving a normalized aggregate brokerage of 0.26 or 26%.

5. Directed data

Both vertex and edge betweenness are directly applicable to directed data and as mentioned above we can apply our extended version of the Koschützki et al. (2005) result. As a consequence we define in-EV-brokerage of a vertex v as follows.

1. Calculate standard directed betweeneess of v, C_B(v).

2. If C_B(v) is non-zero add j to it, where j is the number of vertices that can reach v.

3. Divide each non-zero sum by the in-degree of v.

In a similar way we define the out-EV-brokerage of v as follows

1. Calculate standard directed betweeneess of v, C_B(v).

2. If CB(v) is non-zero add k to it, where k is the number of vertices that v can reach.

3. Divide each non-zero sum by the out-degree of v.

We then define the EV-brokerage of v as the average of the in-EV-brokerage and the out-EV-brokerage of v. This makes the assumption that resources to maintain in-coming ties are the same as those to maintain out-going ties. But if the analyst wants to reflect that maintaining out-going ties uses more resources than incoming ties then they can take a weighted average of the two values rather than the average, or better compare the results with the overall mean. Normalization of in-EV-brokerage, out-EV-brokerage and directed EV-brokerage is exactly the same as the undirected case i.e. using (Eqs. (1) and (2) of Theorem 2.

Table 2 column 1 reports the non-normalized EV-brokerage for the campnet data, shown in Fig. 3 and available in UCINET (Borgatti et al., 2002). Column 1 is the average of columns 2 and 3 which are the in-EV-brokerage and out-EV-brokerage scores for each vertex. Columns 4 and 5 are the sum of the in-edge betweenness and out-betweenness scores for all the edges incident with the vertex and columns 6 and 7 are the in and out degrees of the actors. It follows that column 2 (3) is constructed by dividing elements of column 4 (5) by corresponding entries in column 6 (7). Furthermore, columns 4 and 5 are constructed from columns 8, 9 and 10 as described in the steps above.

Table 2.

Brokerage scores for campnet data given as a percentage.

ID	1 EV-brokerage	2 In-EV-brokerage	3 Out-EV-brokerage	4 Sum in-edge betweenness	5 Sum out-edge betweenness	6 In-degree	7 Out-degree	8 Number in-reachable (j)	9 Number out-reachable (k)	10 Node between-ness
1	26.472	23.833	29.111	95.333	87.333	4	3	17	9	78.333
2	0	0	0	0	0	1	3	6	15	0
3	6.306	9.167	3.444	18.333	10.333	2	3	17	9	1.333
4	11.867	9.9	13.833	49.5	41.5	5	3	17	9	32.5
5	15.146	14.125	16.167	56.5	48.5	4	3	17	9	39.5
6	6.444	7.778	5.111	23.333	15.333	3	3	17	9	6.333
7	7.271	7.375	7.167	29.5	21.5	4	3	17	9	12.5
8	5.958	8.75	3.167	17.5	9.5	2	3	17	9	0.5
9	20.785	18.958	22.611	75.833	67.833	4	3	17	9	58.833
10	0	0	0	0	0	0	3	0	10	0
11	5.167	3.667	6.667	11	20	3	3	6	15	5
12	8.389	8.333	8.444	33.333	25.333	4	3	17	9	16.333
13	0	0	0	0	0	0	3	0	16	0
14	5.111	6.444	3.778	19.333	11.333	3	3	17	9	2.333
15	26.778	30.333	23.222	60.667	69.667	2	3	6	15	54.667
16	7.589	4.567	10.611	22.833	31.833	5	3	6	15	16.833
17	7.236	4.917	9.556	19.667	28.667	4	3	6	15	13.667
18	17.056	13.333	20.778	53.333	62.333	4	3	6	15	47.333

We see that the actor with the highest EV-brokerage, 15, did not have the highest betweenness score which is node 1. In these data the top 3 outgoing ties were used and hence everyone has the same out-degree. However this does not mean that out-EV-brokerage has the same rank ordering as the betweenness scores. We see that node 9 has the second highest betweenness but it is node 15 that has the second highest out-EV-brokerage score.

6. Some extensions and discussion

Computationally the method we propose is of O(nm) where m is the number of edges and n is the number of vertices (Brandes, 2001). This is computationally far more efficient than the VF algorithm and can be used to analyze large sparse networks. Typically in social networks actors need to use resources to maintain ties and so the m will be bounded so that large networks are sparse.

One simple extension is to use some of the many variants of betweenness. In their paper Valente and Fujimoto use average reciprocal distance as their cohesion measure. This of course gives less value to longer paths. The software package UCINET (Borgatti et al., 2002) has an implementation of betweenness which also allows for the weighting of longer paths so they contribute less or ignoring paths that are longer than a prescribed value. Either of these could be used to extend the brokerage method described here. UCINET also has an attribute weighted betweenness measure that incorporates attribute values of the vertices on the geodesic paths. For valued data flow betweenness can be used as an alternative to the regular betweenness scores. All these extensions use node betweenness rather than edge betweenness but given the relationship between the node and the edge version this is not seen as a major issue. We do not pursue any of these (or any other obvious extensions here) but merely highlight these as possibilities analysts could explore if it was relevant for their data. In addition Brandes (2008) gives a number of variants on shortest path centrality algorithms and these can all be used as a basis for node brokerage measures. These readily available extensions make us optimistic that the many uses to which centrality measures have been put, will now be applied to brokerage.

One of the central preoccupations thus far in the study of social networks has been to develop various measures of centrality. This is to be expected as central positions are important to many processes on, for, and of networks. Brokerage, on the other hand, has received considerably less attention, perhaps in part because it can be less intuitive to understand what occupying a brokerage position means (it is not prominence, for example), and perhaps because it is unclear whether brokerage is advantageous or deleterious. By introducing several computational methods for calculating brokerage, and highlighting the various measures available, we hope to stimulate more research on how to conceptualize, measure, and understand brokerage in networks.

Like centrality measures, we offer various nuanced definitions of what it means for a node to occupy a brokerage position. Brokerage can be characterized as having links that reduce the overall cohesiveness (as measured by inverse distances) of a network, or they can be nodes with links that have high betweenness, or those which disconnect a graph when removed. In the EV and VF expositions, the chief insight was to calculate brokerage by dividing by each node’s degree. Although this conceptually need not always be the case, to date this seems the key distinguishing feature between brokerage and centrality. A an actor incident with many bridge like connections is central, one with few, is a broker.

Node centrality has been associated with processes that occur on networks such as diffusion of innovations (Rogers, 2003), opinion leadership (Valente and Davis, 1999), and behavioral influences (Alexander et al., 2001). Some studies have linked brokerage to similar processes, notably Burt’s application of constraint and brokerage to success (Burt, 1995). Other research has confirmed, contradicted, and expanded the association between brokerage and outcomes. These studies, however, have relied on brokerage measures confined to the local, neighborhood environment: Constraint, a useful and flexible measure of brokerage requires only the local neighborhood for its computation. While this is certainly an advantage, it is possible that sociometric measures of brokerage, defined and elaborated here, may provide more insights into how occupying a brokerage position can affect such outcomes.

In addition, our intuition is that a macro-level understanding of how “bridgeable” a network is, that is, the extent that the network is characterized by one or a few brokers/bridges will provide important insights into role of network structure on outcomes. A highly brokered network is likely more vulnerable to attack, and more dependent on one or a few actors to remain functional. Such structures are likely unstable and being able to measure such structures is likely to provide important diagnostics for organizational and community performance.

We do not feel this is the last word on brokerage or bridging, but hope that we have clarified some of the conceptual and mathematical underpinnings of these concepts so they can be applied more readily to substantive phenomena.