Abstract
To conduct a patient-specific computational modeling of the aortic valve, 3D aortic valve anatomic geometries of an individual patient need to be reconstructed from clinical 3D cardiac images. Currently, most of computational studies involve manual heart valve geometry reconstruction and manual FE model generation, which is both time-consuming and prone to human errors. A seamless computational modeling framework, which can automate this process based on machine learning algorithms, is desirable, as it can not only eliminate human errors and ensure the consistency of the modeling results, but also allows fast feedback to clinicians and permits a future population-based probabilistic analysis of large patient cohorts. In this study, we developed a novel computational modeling method to automatically reconstruct the 3D geometries of the aortic valve from CT images. The reconstructed valve geometries have built-in mesh correspondence, which bridges harmonically for the consequent FE modeling. The proposed method was evaluated by comparing the reconstructed geometries from ten patients to those manually created by human experts, and a mean discrepancy of 0.69 mm was obtained. Based on these reconstructed geometries, FE models of valve leaflets were developed, and aortic valve closure from end systole to mid-diastole was simulated for seven patients and validated by comparing the deformed geometries to those manually created by human experts, and a mean discrepancy of 1.57 mm was obtained. The proposed method offers great potential to streamline the computational modeling process and enables the development of a pre-operative planning system for aortic valve disease diagnosis and treatment.
Keywords: aortic valve geometry reconstruction, cardiac image analysis, machine learning, aortic valve finite element model
1. INTRODUCTION
Noninvasive cardiac imaging modalities, such as echocardiography, cardiac magnetic resonance imaging, and computed tomographic imaging (CT) are now used extensively for heart valve disease diagnosis and risk evaluation. Although most valvular disease evaluation is performed on two-dimensional images, patient cardiac image data can offer 3D volumetric, time-resolved data, allowing the 3D reconstruction of anatomical heart valve geometries. When integrated with computational models, such as finite element (FE) models, native heart valve function can be investigated, and pre-operative planning tools can be developed to assess a particular interventional procedure for individual patients (1).
Computational models (2–9) have been developed to investigate the structural biomechanical interaction between the native aortic root and a deployed transcatheter valve during the transcatheter aortic valve replacement (TAVR) procedure. One of the limitations of these studies is that the development of a 3D aortic valve computational model from 3D clinical image data often requires manual annotation software (e.g. Avizo or Mimics), which is tedious and time-consuming, preventing fast feedback to clinicians and accurate model prediction. More importantly, all current models lack mesh correspondence, i.e., different number of nodes and different element connectivity between different patients, preventing patient-population based computational analysis. Thus, an image analysis method for automatic 3D aortic valve geometry reconstruction with built-in mesh correspondence will greatly facilitate computational modeling of the aortic valve.
Currently, most of the studies on automatic cardiac image segmentation and geometry reconstruction (10–16) focus on shape estimation of the left and right atriums and ventricles, the ventricular outflow tract, and the aorta. There are a few works related to valve shape estimation. Zheng et al. (17) developed a method for aorta segmentation and landmark detection from 3D C-Arm CT images, which was aimed for 3D visualization during transapical aortic valve implantation. Pouch et.al. (18) proposed a method based on intensity-based image registration to estimate aortic leaflet shapes from 3D echocardiographic images requiring only three landmarks chosen by the user. Ionasec et al. (19) proposed a new method for geometry reconstruction of the mitral-aortic complex from 3D CT images, utilizing a large number of aortic valve shapes (more than 600) manually delineated from 3D images to serve as training data. To ensure that the meshes have no tangled faces, Palmer et al. (20) developed an aortic root segmentation method with shape constraints and mesh regularization. The primary motivations for these aortic valve shape reconstruction methods have been for real-time visualization of valve function in the clinical setting and measurement of key anatomical parameters such as aortic root diameter, not for accurate computational modeling of aortic valve biomechanics.
The objective of this study was to develop a computational framework for patient-specific modeling of the aortic valve (AV). To achieve this goal, we developed a machine learning based image analysis method to automatically reconstruct the 3D geometries of the aortic valve from clinical 3D CT images, and performed FE analysis using the reconstructed geometries. The spatial distribution of the nodes on each aortic valve mesh generated by this method, is highly uniform. All the meshes have correspondence between different patients, which is desirable for the FE model development process and can facilitate a population-based probabilistic analysis of the aortic valve biomechanics.
2. METHODS
2.1 Image analysis method for aortic valve shape reconstruction
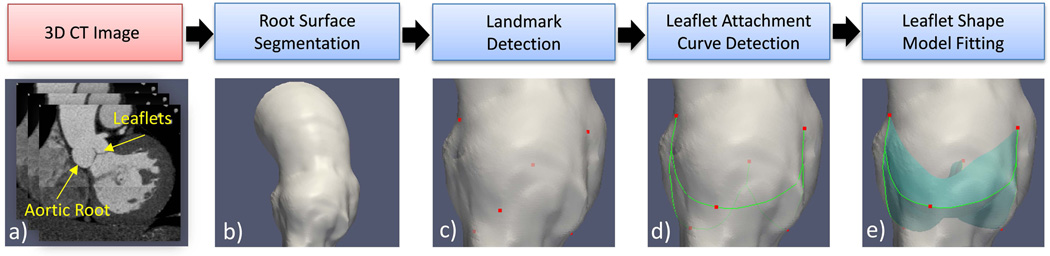
Figure 1 depicts the overall AV shape reconstruction process starting from a 3D CT image of a patient. Briefly, the surface of the aortic root is first obtained via a standard level-set based image segmentation algorithm described in detail in (21–23). Given the aortic root surface, six landmarks are detected by the landmark detectors (section 2.1.4) developed using machine learning techniques and a novel shape dictionary learning (SDL) algorithm to build dictionary-based statistical shape models (D-SSM) (section 2.1.3). Then, the leaflet attachment curves between the detected landmarks are found by the curve detectors (section 2.1.5) similar to the landmark detectors. Finally, given the detected leaflet attachment curves, the leaflet shape model is fitted to the input image (section 2.1.6) using a novel linear coding (LC) based algorithm for shape model fitting, to obtain the leaflet geometry represented by single-layer triangle meshes. All the algorithms were implemented in C++ and Matlab.
Figure 1.
The shape reconstruction process illustrated by the steps of a) an input 3D CT image composed of 2D slices. b) Root surface segmented from the input image. c) Detected Landmarks (red dots) on the root surface d) Detected leaflet attachment curves (green curves) on the root surface. e) leaflet geometry reconstructed by model fitting. The input image a) is used in all the steps from b) to e).
2.1.1 Image data
Full phase cardiac multi-slice CT (MSCT) scans were collected from patients at Hartford Hospital (Hartford, CT) (24). Institutional Review Broad approval to review de-identified images was obtained for this study. Image data from ten patients (4 females and 6 males) between the ages of 48 and 85 years, who did not have severe aortic stenosis, calcification, or bicuspid aortic valve, were selected for this study. The MSCT examination was performed on a GE LightSpeed 64-channel volume computed tomography scanner. The spatial resolution of the image data was 0.49×0.49×1.25 mm, and the temporal resolution was less than 200 ms depending on the heart rate and pitch. Typically, image data encompassing 10 phases over the cardiac cycle were obtained for a patient.
2.1.2 Generation of training set of aortic valve shapes with mesh correspondence
The training set of aortic valve shapes was generated in two steps: 1) segmentation of aortic valve images and manual generation of aortic valve meshes; and 2) automatic remeshing to establish mesh correspondence.
Step 1 Manual Annotation
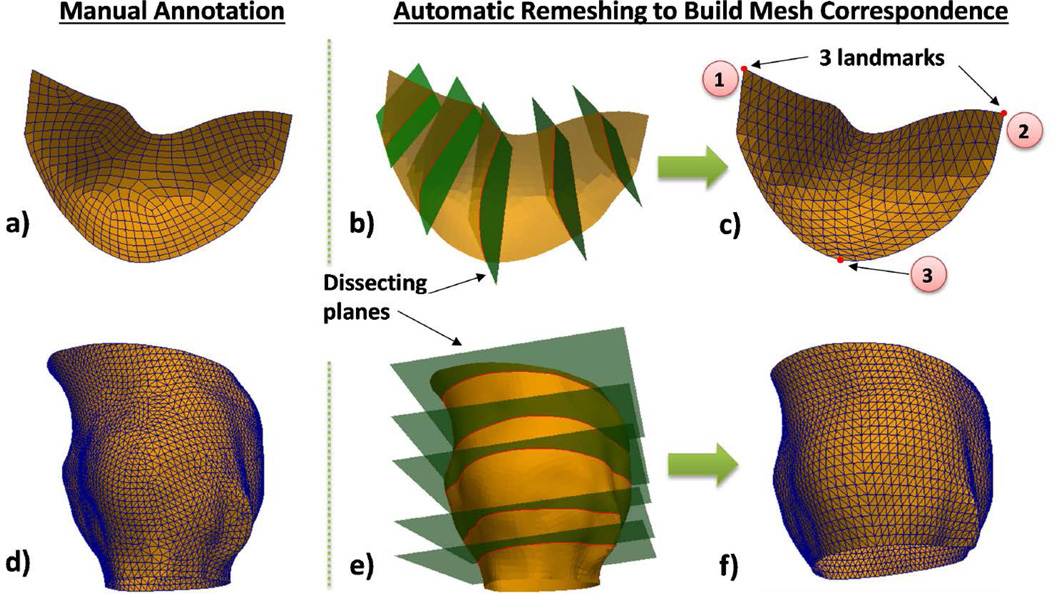
First, 1) Aortic valve surface geometries were manually segmented from CT images by human experts using image visualization software Avizo (FEI, Burlington, MA): the aortic root was segmented by using intensity thresholding and pixel editing, and the leaflets were segmented by using the brush tool. 2) The segmentation results were imported in Hypermesh (Altair Engineering Inc., MI) to generate surface meshes by identifying the leaflet attachment curves and then stitching the meshes of leaflets and the mesh of the root surface together. 3) The resulting meshes were superimposed with the raw image data to check for potential discrepancies, and 1)&2) were repeated if necessary until the meshes reached the desired quality visually judged by the operator. This approach is very similar to those (6, 25–27) in the literature. These meshes (Figure 2a&d) do not have correspondence between different patients: each mesh has a different number of nodes and different element connectivity.
Figure 2.
(a) Manually generated meshes of a leaflet and (d) an aortic root surface; automatic remeshing achieved by cutting the leaflet (b) and root (e) surfaces using planes and resampling the intersection curves to obtain the final meshes of the leaflet (c) and the root (f). Three landmark points are used: ①left commissure, ②right commissure, ③hinge. Since mesh topology is fixed for all the patients, mesh correspondence is established.
Step 2 Automatic Remeshing
We developed a remeshing method based on cut-planes (28) to build aortic valve meshes with correspondence between patients (Figure 2a–c). Briefly, the boundary curve of the random leaflet mesh from Step 1 is evenly resampled into a set of points (i.e., nodes), and a set of cut-planes are used to cut the leaflet surface to produce a set of intersection curves at these points. Each of the cut-planes is perpendicular to the plane defined by three anatomical landmarks: two commissure points and one hinge point (Figure 2c), and pass two points of the resampled boundary curve: one point on the lower boundary (left-commissure to hinge to right-commissure) and one point on the upper boundary (left-commissure to right-commissure). By resampling these intersection curves and triangulating the sampled points, a new leaflet mesh is built consistently, and mesh correspondence between patients is maintained by the fixed mesh topology.
A similar approach is used for remeshing the aortic root surface, shown in Figure 2d–f. The aortic root surface is cut with a set of parallel planes (i.e. cut-planes) spaced at equal distances to produce a set of intersection curves. The bottom cut-plane contains the three hinges of the three leaflets. To align the cut-planes to the landmarks, the normal vector N of a cut-plane is adjusted by N = aN1 + (1 − a)N2, and a = 1 − dist1/(dist1 + dist2) if the cut-plane is below or level with the plane determined by the three commissures of the three leaflets. Here, N1 is the normal vector of the plane determined by the three hinges, N2 is the normal vector of the plane determined by the three commissures, dist1 is the distance between the cut-plane and the average position of the hinges, and dist2 is the distance between the cut-plane and the average position of the commissures. If the cut-plane is above the plane determined by the commissures, then its normal vector is equal to N2. By resampling these intersection curves and triangulating the sampled points, a new root surface mesh is built consistently with mesh correspondence between patients.
2.1.3 Algorithms for building dictionary-based statistical shape model
In this study, we developed a novel shape dictionary learning (SDL) algorithm based on sparse coding with locality-induced sparseness (29, 30) which is a technique in machine learning, to build a dictionary-based statistical shape model (D-SSM) without any assumption of shape distributions. The SDL algorithm is used for building landmark detectors (section 2.1.4) and leaflet attachment curve detectors (section 2.1.5).
A shape dictionary is a collection of different shapes, where a shape d(m) in the dictionary D = [d(1), …, d(m), …, d(M)], is a mesh describing the geometry of an object, and can be represented by a column vector containing all the point coordinates of the mesh. A D-SSM is a dictionary of representative shapes that can well describe a shape distribution. The SDL algorithm consists of two parts: Part-1 is to build an initial shape dictionary, and Part-2 is to refine the shape dictionary. Part-1 and Part-2 both use the same training data. The details of the SDL algorithm Part-1 and Part-2 are provided in the tables Algorithm-1 and Algorithm-2 in the appendix, respectively. Here we briefly describe the key concepts of the SDL algorithm. Randomly selected training shapes may be used to assemble an initial dictionary; however, the shapes in the initial dictionary must exhibit a large range of variation. In some cases, the randomly selected training shapes can be very similar to each other, resulting in bad initialization. Thus, in Part-1 of the SDL algorithm, training shapes are selected such that the average similarity between the selected shapes in the initial dictionary is minimized. Starting from the initial shape dictionary, in Part-2 of the SDL algorithm, the dictionary is updated such that it can better represent the shape distribution than the initial dictionary. At each training cycle, a shape in the dictionary is updated by a weighted linear combination of this shape and several other training shapes. Therefore this shape in the dictionary can represent not only itself but also some other shapes in the training set, and as a result, the whole dictionary can better represent the shape distribution. Note that the SDL algorithm is in an on-line style (31), i.e. it uses a small subset of the training shapes at each training cycle, which can reduce computer memory usage.
2.1.4 Landmark detection
We built landmark detectors to automatically locate the 6 anatomical landmarks at 3 commissures and 3 hinges (Figure 1c and Figure 2c), given the aortic root surface. To locate the commissures, first, we built a single-commissure detector that can find the commissures individually; and then, to improve computational efficiency, we built a joint-commissure-detector upon three single-commissure detectors, to find the three commissures simultaneously. Hinge detectors were built in the same way. The details of commissure detectors are described as follows.
Detecting a single landmark point is equivalent to detecting the local shape of the heart near that point. Using the SDL algorithm in section 2.1.3, a dictionary of local shapes around the commissures was built. An example of local shapes is given in Figure 3b. For each local shape d(m) in the dictionary, a standard logistic-regression based classifier (32) was trained by using the image features extracted at the points of that local shape. Training samples of image features can be obtained by sampling the image region around the aortic root. Once the classifier is trained, given the image features extracted according to the local shape d(m) at a candidate point pc, the classifier will output a confidence value hm(pc) which will be high if the point pc is near a commissure. The single-commissure detector is a set of such classifiers, and it outputs the maximum confidence value at a candidate point pc, i.e., max{h1(pc), …, hm(pc), …}. The output hm(pc) of the classifier associated with d(m) is given by
| (1) |
where , and is a spatial point, and {λ0, …, λJ} are scalar coefficients determined by logistic regression (32, 33). The function is defined as
| (2) |
Here, and are image intensities at two spatial points and . Recall that d(m) is also a mesh composed by some points from the root surface mesh and some points from the leaflet meshes as shown in Figure 3(b). If the point of d(m) is from the root surface mesh, then (i.e. inside the root) and where is the mesh normal at point and ρ is set to 2mm in experiments. If the point is from the leaflet meshes, then and . σm is the standard deviation of local pixel intensities, which is calculated by using the pixel intensities sampled at the points . ε is a scalar determined by a brute-force search approach.
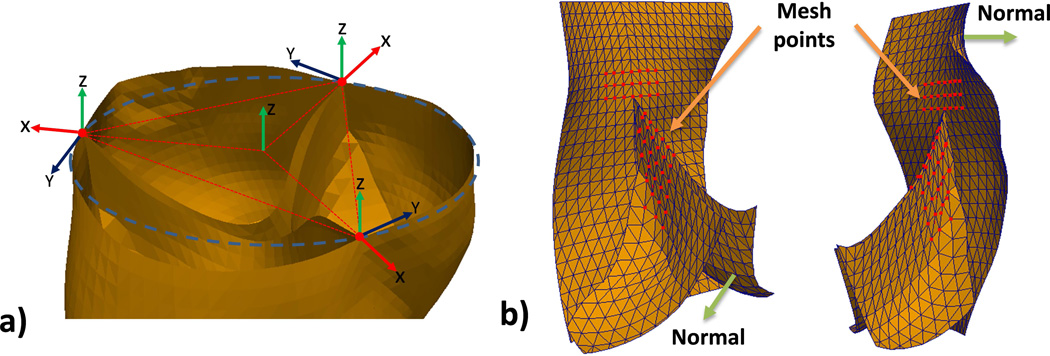
Figure 3.
a) Example of the Local Coordinate Systems determined by three candidate points (red). In this example, the three candidate points happen to be exactly the same as the commissure points; b) A local shape around a commissure, which is composed of the selected mesh-points (red).
A joint-commissure-detector was built to find the three commissure points simultaneously for computational efficiency, and it is obtained by simply arranging three single-commissure-detectors along a circle with three local coordinate systems as shown in Figure 3a. Given the diameter of the circle (i.e. aortic root diameter) and three candidate points on the circle, the joint-commissure-detector outputs the average of the confidence values from the three single-commissure-detectors positioned at the candidate points. After scanning the root surface with a range of feasible diameters, the joint-commissure-detector will find three points with the highest confidence value as the commissure points.
2.1.5 Leaflet attachment curve detection
Once the landmarks (three commissures and three hinges) are found, the leaflet-sinus attachment curves (Figure 1d) between these landmarks are obtained by evaluating candidate curves on the aortic root surface and selecting the best one. The candidate curves are generated by connecting the points on the aortic root surface mesh between a commissure point and a nearby hinge point in different ways. The optimal curve is then identified by using a point detector similar to the single-landmark detectors in section 2.1.4. The point detector was built to evaluate the likelihood of a point being on the attachment curves. The score of a candidate curve is the sum of the detector outputs (confidence values) at individual points of the curve. Between two landmarks, the candidate curve with the highest score is selected and then resampled at equal intervals to obtain the same number of points as the leaflet attachment curves on the leaflet meshes.
2.1.6 Leaflet shape model fitting
Following leaflet attachment curve detection, the leaflet shape dictionary (i.e. shape model) is fitted to the input 3D CT image, I, to infer the unknown shape, X, of the leaflets in the input image, using a linear coding (LC) based algorithm we developed. The algorithm has four steps.
Step-1
Transform all the shapes in the dictionary to the image space by using thin plate spline (TPS) transform (34) according to the detected leaflet attachment curves to obtain a transformed dictionary: D̃ = [d(1), …, d(m), …, d(M)]. Each shape d(m) represents the geometry of three leaflets inside the aortic root, and consists of three triangle meshes (Figure 2c).
Step-2
Find a subset of shapes {d(m1), … d(mk), …, d(mK)} in the transformed dictionary, which are the most similar to the unknown shape X, by measuring the similarity defined as:
| (3) |
Here, is a point, and K is set to 3 in experiments. is the pixel intensity at point in the filtered image Ig which is obtained by first computing the gradient magnitude image from the input image I, and then performing isotropic Gaussian-filtering with sigma equal to 2mm. The rationale is that if d(mk) is similar to X, then the image gradient magnitude will be high near each point of d(mk), because in a 3D CT image, the pixel intensity level of the leaflets is much lower than the pixel intensity level of the surrounding blood inside the root.
Step-3
Perform linear coding (LC) to infer the unknown shape by
| (4) |
with the following constraint on the coefficients: , ck ≥ 0. A brute-force search is utilized to obtain the optimal coefficients such that the summation of the image gradient magnitudes near X̂ is maximized, i.e., maximizing the objective function E(X̂) defined by
| (5) |
Here, the shape X̂ is a mesh composed of three meshes of three leaflets, where X̂ = [p1, …, pi, …, pL] and pi is a spatial point, L is the total number of points, qi is a point inside the blood pool, and qi = pi − pni, ni is the leaflet mesh normal at point pi, ρ is set to 2mm in experiments, and I(pi) is the image intensity at point pi. Again, the rationale is that if X̂ is close to X, then the image gradient magnitude will be high near each point of X̂, because the pixel intensity level of the leaflets is much lower relative to that of the surrounding blood pool.
Step-4
Refine the mesh X̂ by iteratively deforming it locally to the image intensity boundary along the mesh normal directions and applying a standard mesh smoothing algorithm (28). The resulting deformed X̂ is the reconstructed geometry of the leaflets from the input image, represented by three triangle meshes as shown in Figure 1e. Since mesh correspondence exists among the shapes in the shape dictionary, and the reconstructed shape has the same mesh topology as the shapes in the dictionary, then the reconstructed shape has the same mesh correspondence.
2.1.7 Validation of the image analysis method
The 3D CT images of the ten patients studied were used for validation of the proposed image analysis method in a leave-one-out approach (32). Accordingly, 1) 9 patient data were randomly selected to create a training set (section 2.1.2). 2) The training set was used to train the algorithms of the image analysis method (sections 2.1.3–2.1.6). 3) The image analysis method was applied to the 3D image of the remaining patient not included in the training set, to automatically reconstruct the AV geometry. 4) The reconstructed geometry was compared to that manually created by human experts using the point-to-mesh distance metric (18) to calculate the reconstruction error, assuming the manually created meshes as the ground truth. The point-to-mesh distance metric between two surface meshes S1 and S2 is the average distance between a point (on S1, S2) and a surface (S2, S1). The process was repeated ten times to obtain the mean and standard deviation of the reconstruction errors.
2.2 Finite Element (FE) modeling of the aortic valve leaflet deformation
Patient-specific FE modeling of the aortic valve was performed for seven patients to analyze in vivo valve closure from end systole to mid diastole. To simply the FE study, the aortic root deformation was not simulated, thus only the valve leaflets were considered in the FE study. By using the proposed image analysis method, the initial geometries of the valve leaflets were reconstructed at the end systole phase, where the leaflets are partially open and assumed to be in the stress-free state. The triangle meshes were extruded by a uniform thickness of 1 mm, which is typical for human aortic leaflets (35), to obtain AV FE models with 6-node “brick” elements (1536 C3D6 elements). Then FE simulations of aortic valve closure from end systole to mid diastole were performed.
2.2.1. Aortic valve material modeling
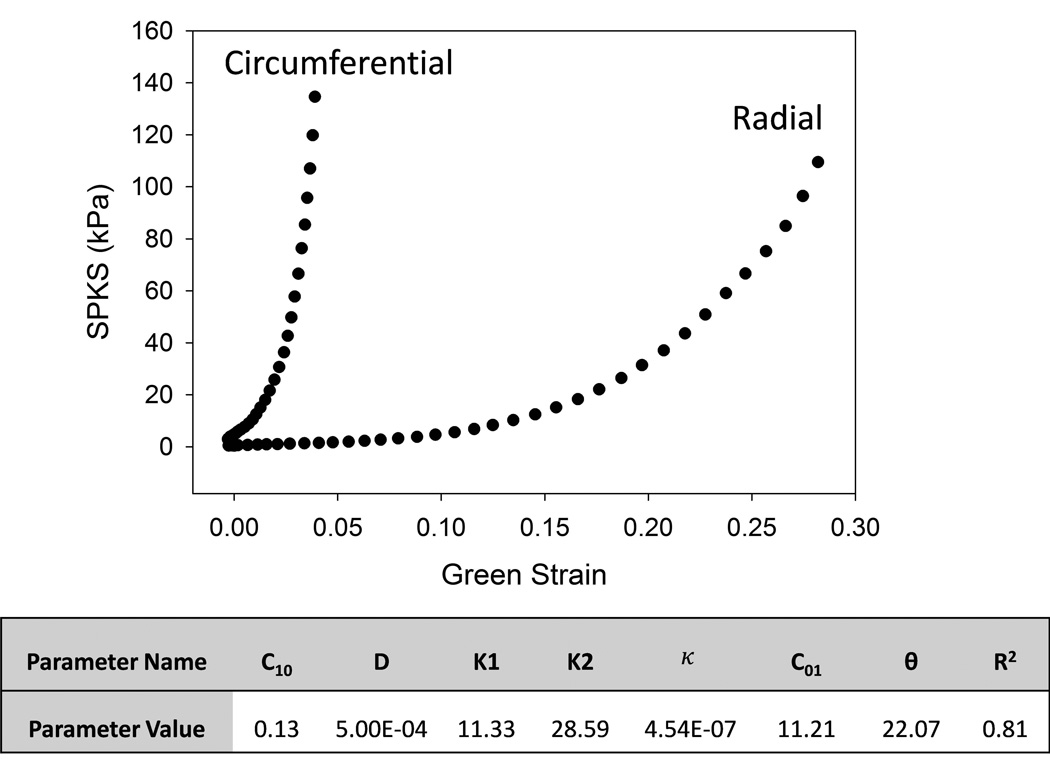
Human AV leaflet material properties were adopted from a 80 year old female patient in Martin and Sun (35) for this study, as shown in Figure 4. The leaflet mechanical behaviors were modeled with a modified Holzapfel-Gasser-Ogden material model (36). The strain energy function, W, can be expressed as:
| (6) |
where C10, C01, k1, k2 and D are material constants determined through fitting of the experimental data, Ī1 and Ī4i are the strain invariants, κ is a dispersion parameter, and J is the determinant of the deformation gradient. The fiber orientation was defined through Ī4i = m0i · Cm0i, where C is the right Cauchy Green tensor, with m01 = [cosθ, sinθ, 0] and m02 = [cosθ, − sinθ, 0], and θ is the angle between the fiber and the circumferential direction. The material model was implemented into ABAQUS Explicit 6.13 (SIMULIA, Providence, RI) (37).
Figure 4.
The stress-strain responses of aortic leaflets obtained from biaxial tests of a human cadaver heart. The table displays the material parameters and the goodness of fit (R2) obtained from model fitting.
2.2.2 Loading and boundary conditions
Aortic valve closure was simulated in Abaqus Explicit in a two-step analysis. In the first step, nodal displacements were prescribed at each leaflet attachment curve (ATC) of the FE model as kinematic boundary conditions to describe the motion of the aortic root from end systole to mid diastole. By using the proposed image analysis method, the nodal boundary conditions were determined by the reconstructed AV geometries. Since mesh correspondence is established by the image analysis method, the displacement of each node on the ATC from end systole to mid diastole was obtained by measuring the displacement between corresponding nodes at each respective phase. In the second step, a mean transvalvular pressure of 95 mmHg was applied to the aortic surface of each leaflet to simulate valve closure. The deformed valve leaflet geometry and strain values were extracted and analyzed.
2.2.3 FE model validation
FE model validation was performed by comparing the mid-diastolic deformed valve leaflet geometries from the FE simulations to those manually created by human experts, and point-to-mesh distances were computed to quantitatively determine the error in the FE predicted end-diastolic geometries. Again, the manually created meshes were assumed as the ground truth. Based on the resolution of the CT images (0.49×0.49×1.25 mm), a mean error greater than 2 mm was considered to be significant.
3. RESULTS
3.1 Automatic aortic valve shape reconstruction
The proposed image analysis method was evaluated on clinical 3D CT images at the end systole phase from ten patients in a leave-one-out approach (section 2.1.7). The reconstruction accuracy was measured by comparing the reconstructed shapes to the “ground truth” shapes generated manually by human experts using the point-to-mesh distance metric (section 2.1.7). We also tried to compare the proposed method with the related methods in the literature. However, direct comparisons with those methods are problematic because different methods are designed for different applications with different imaging modalities. Nonetheless, the results of the related methods are cited directly from the corresponding papers.
The landmark detection accuracy achieved with our proposed method is compared with that obtained by Zheng et al. (17) in Table-1. The results demonstrate the ability of the landmark detectors built upon the local shape dictionaries. The aortic valve shape reconstruction accuracy obtained in this study, 0.69±0.13 mm, is compared to that obtained by the method proposed by Ionasec et al. (19) in Table-2: the results demonstrate the ability of the linear coding based shape inference algorithm. We also tested the proposed method with manually obtained landmarks, i.e. landmark detectors were disabled (Proposed* in Table-2).
Table-1.
Landmark Detection Accuracy (unit: mm)
| Method | Modality | Resolution | Hinge Error | Commissure Error |
|---|---|---|---|---|
| Proposed | CT | 0.49×0.49×1.25 | 1.90±1.41 | 2.00±1.43 |
| Zheng et. al 2012 (17) |
C-arm CT | 0.7~0.84 isotropic | 2.09±1.18 | 2.17±1.31 |
Table-2.
Shape Reconstruction Accuracy (unit: mm)
| Method | CT Resolution | valve | Landmark | Error |
|---|---|---|---|---|
| Proposed | 0.49×0.49×1.25 | aortic | auto-detect | 0.69±0.13 |
| Proposed* | manual | 0.65±0.11 | ||
| Ionasec et al. 2010 (19) |
in slice: 0.28~1 thickness: 0.4~2 |
aortic & mitral | auto-detect | 1.36±0.93 |
3.2 Aortic valve FE model simulation
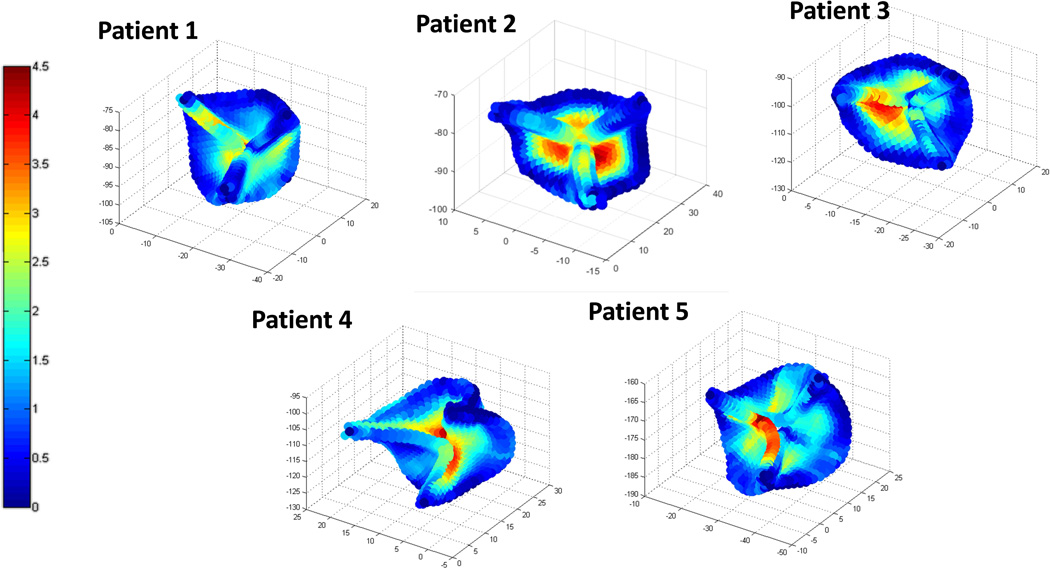
The deformed FE valve meshes of the seven patients at mid diastole were obtained and compared to those manually created by human experts. As reported in Table-3, the average point-to-mesh distance was 1.57 mm. The distributions of the distances for five patients with less than 2 mm average point-to-mesh distance are plotted in Figure 5. The distances were the largest at the regions near the belly (center of the leaflet) and the nodule near the free-edges.
Table-3.
Accuracy of Deformed FE geometries
| Patient ID | Age | Error (mm) |
|---|---|---|
| 1 | 75 | 1.25±0.78 |
| 2 | 85 | 1.52±1.08 |
| 3 | 61 | 1.35±1.02 |
| 4 | 68 | 1.33±0.82 |
| 5 | 73 | 2.03±1.52 |
| 6 | 73 | 1.43±1.01 |
| 7 | 69 | 2.09±1.50 |
Figure 5.
3D representation of the point-to-mesh distance errors between the deformed FE meshes and those manually created by human experts for five patients. (Unit: mm)
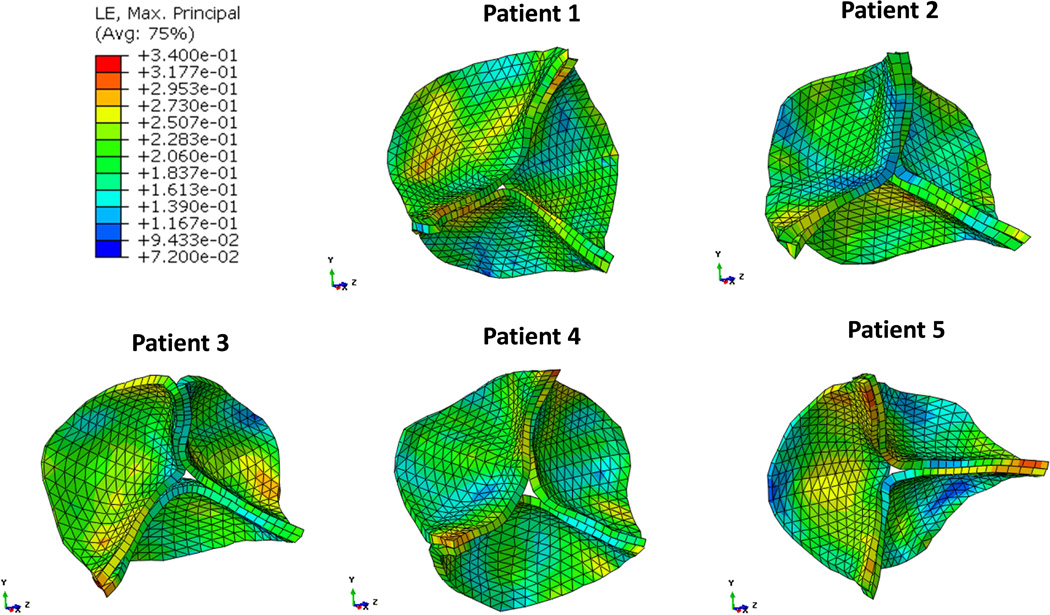
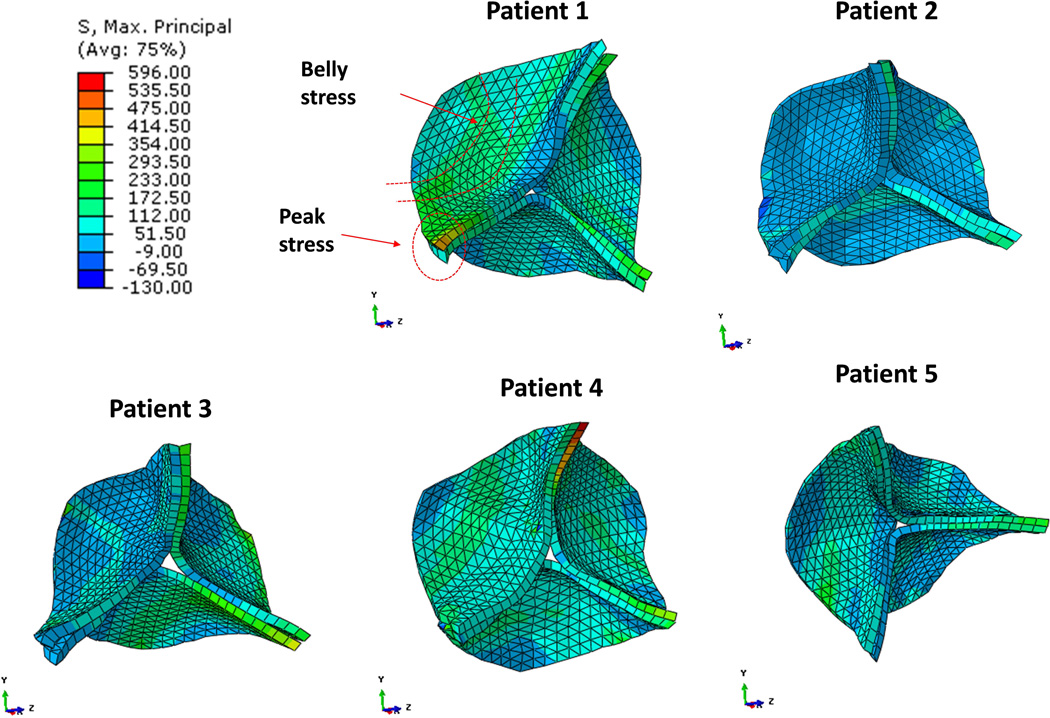
The strain distributions of the five valve models with average point-to-mesh distance less than 2 mm are shown in Figure 6. The stress-strain patterns were different among all the patients or among the three leaflets of each individual patient due to the asymmetrical geometries. Overall, the maximum principal strain was more uniform in the belly region with average values ranging 0.18 to 0.25 during valve closure. Peak strain of 0.34 was observed at the commissural regions. Figure 7 shows the valve maximum principal stress from the five patients at the same aortic valve closure phase. The stresses were 172 – 354 kPa at the center of the belly regions, and were highest near the commissural regions, 475 – 596 kPa. Compressive stresses were observed at regions near the leaflet attachment line and at free-edge regions where leaflets were coapted and became slightly corrugated.
Figure 6.
Maximum principal strain distributions in the circumferential (top) and radial (bottom) directions during diastole from five patients.
Figure 7.
Maximum principal stress distributions during diastole from five patients.
4. DISCUSSION
Advantage of the proposed image analysis method
Reconstruction of the aortic valve shape from 3D CT images is challenging because the thickness of the leaflets is small, ~1 mm, which is much smaller than 2 pixels in the 3D CT images with resolution 0.49×0.49×1.25 mm, and the aortic valve shape varies across different patients. Simple algorithms such as intensity thresholding are insufficient for AV segmentation, and the level-set based image segmentation algorithms (21, 22) can automatically identify the surface of relatively large objects such as the aortic root surface, but are not effective for small and thin leaflets. Thus, we developed a novel image analysis method with several algorithms assembled in a pipeline (Figure 1). The method utilizes machine learning techniques for building shape models and training classifier-based detectors to leverage prior knowledge about aortic valve shapes.
In this study, we proposed a SDL algorithm for building a D-SSM of the AV local shapes used for classifier-based detectors. These shape dictionaries eliminate the need for feature location searching during the training of the classifiers, and therefore only a relatively small amount of training data is required, compared to the related methods (17, 19) which used hundreds of training images. Once the type of image features is determined (e.g. image gradient), image feature selection is used to find the optimal locations in the images to extract those image features. In the literature (13, 17, 32, 38), feature selection is usually conducted in a brute-force search manner, and a substantial amount of training data is required to find the features that are statistically significant. Using our method, since we have the dictionaries of the local shapes, we only need to extract image features at the points of the local shapes, and image features at other locations are simply irrelevant or unnecessary. In this study, the type of features were pre-determined, i.e., handcrafted. Recently, deep learning methods have been successfully used for image segmentation (39–42), in which features are learned automatically. We will combine deep learning and the D-SSM in future work.
We proposed a LC based algorithm to infer the unknown shape of the AV from image data by using the leaflet shape dictionary. The shape dictionary is spatially transformed to the image space according to the detected leaflet attachment curves, and then the transformed shapes become more similar to the unknown shape than the original shapes. The transformed dictionary represents the shape distribution conditioned on leaflet attachment curves, which is better than the original dictionary. Therefore, again, this means only a relatively small number of training shapes are required. As pointed out by Palmer et al. (20), mesh self-intersection could occur during mesh deformation and can be solved by using mesh regularization. The LC based algorithm can also ensure that AV meshes have no self-intersection because a linear combination of meshes of similar shapes will not lead to self-intersection as long as the individual meshes have no such issue.
The D-SSM approach is very generic for shape modeling. Coupling with the LC based shape inference algorithm, the D-SSM approach may be used for geometry reconstruction of other objects from medical images. A D-SSM represents the probability distribution of shapes from a certain population. The traditional principle component analysis based statistical shape model (PCA-SSM) (34, 43) assumes a Gaussian distribution, and therefore may not represent irregular distributions in real situations. Based on sparse coding with locality-induced sparseness (29, 30), D-SSM models do not assume any particular distribution and are capable of representing any kind of distribution.
Finite element modeling of the human aortic valve
The built-in mesh correspondence is highly attractive for FE analysis. From one simulation to another, only the nodal coordinates and boundary conditions had to be updated: the material property, element and surface definitions (for the pressure loading conditions) could remain unchanged. The mesh correspondence facilitated the definition of patient-specific ATC boundary conditions from end systole to mid diastole. We found that the dynamic motion of the aortic roots described by the displacement of the ATC in the model was crucial for achieving proper AV closure. Without changing the ATC locations, the leaflets were not able to close properly.
The simulation results were consistent with AV FE results presented in the literature. The physiological stress-strain distributions of the patient valves during closure were not uniform among the three leaflets or within a single leaflet. This finding is consistent with results by Grande et al. (44) where they found varying stresses and strains across the leaflet area. They reported average leaflet peak stresses of 482 kPa at the belly near the coaptation surfaces for all leaflets. In our models, stresses at the belly regions were lower, between 60 – 279 kPa. The peak stresses ranging from 121 – 457 kPa were found at the commissure regions in our models; however, Grande et al. (44) found peak stress of 537 kPa at the free margin, where we found much lower stresses ranging 8 – 80kPa. This discrepancy could be in part due to differences in their model (44) versus ours including: the thickness definition - varying thickness across valve leaflet versus our uniform thickness assumption, the constitutive models used - linear elastic versus our nonlinear hyperelastic model, and the source of the experimental tissue property data used - animal versus our human data. Our finding of highest stress at the commissure region was in agreement with the FE study of 10 human AV models by Labrosse et al. (27), who consistently found highest stress at the top of the commissures with a magnitude of 1,007 ± 719 kPa. The relatively lower stress on the free-edge region observed in this study was in agreement with a study by Conti et al. (45) where the leaflet free-margin zone stresses ranged from 0 – 12 kPa for the non-coronary leaflet and between 0 – 42 kPa for the right and left coronary leaflets. The maximum stresses in the belly regions of the leaflets of 603 – 759 kPa reported in (45), were consistent with our results. However, the minimum stresses reported in (45) were lower compared to in our models (<12 kPa versus 20 – 23 kPa). This discrepancy could be due to differences in the aortic valve leaflet material property definitions—in (45) the leaflets were prescribed the highly compliant response of the porcine aortic valve, whereas the leaflets were prescribed the much stiffer response of the aged human aortic valve in this study.
Clinical relevance
This work integrates the automatic extraction of 3D aortic valve geometries from clinical image data and the generation of FE models with mesh correspondence, in the development of a seamless computational modeling framework for efficient patient-specific AV analyses. One potential application of this framework is to model the TAVR deployment process. Patient-specific TAVR computational models could be used to investigate the biomechanical interaction between the device and the surrounding tissue in order to determine the proper TAVR device, sizing, and positioning for an individual patient to maximize the likelihood of success. There are several patient-specific TAVR computational models presented in the literature (2–7); however, these models were developed without automatic segmentation of image data and automatic FE model generation. The clinical image-to-AV model procedure developed in this study will be expanded in future studies to include valve calcification and surrounding tissues. Ultimately, we hope this procedure could facilitate efficient and accurate model prediction, making simulation-based pre-TAVR planning a clinical reality.
Furthermore, the D-SSM developed in this study will enable large population-based computational studies. Given the D-SSM model of the aortic valve, a new aortic valve shape of a virtual patient can be generated by using the LC algorithm (section 2.1.6) in three steps: 1) randomly select a few shapes from the dictionary; 2) randomly choose a set of coefficients stratifying the constraint associated with Eq.(4); 3) compute the new shape using Eq.(4). By sampling from the shape distribution represented by the D-SSM, we can generate a large variety of new aortic valve shapes of virtual patients with mesh correspondence between these virtual patients, and use these shapes to build computational models and perform probabilistic analysis. Such analyses for TAVR, for instance, would provide insight into improved TAVR device design, sizing and positioning guidelines, and patient-screening criteria.
Limitations
Only one set of human material properties was used in the FE simulations. The in vivo material properties of the 7 patients are likely to be different from the material properties that we obtained from the explanted cadaver heart. In this study, the data from an 80 year old female patient was used, which might be representative of aged human valve responses. Currently there is a lack of databases of human material properties, thus, we cannot even have age- and gender- match between the modeled patient and available ex vivo data. In addition, we assumed that AVs have homogeneous properties and a uniform thickness. It has been shown that AV tissue properties vary at different regions, e.g., between the belly and commissure regions (46). Since the current biaxial testing method can only measure material properties of a small region (~5 × 5 mm2), more sophisticated testing and modeling tools are needed to characterize regional properties of the aortic valve. The CT data used in this study had relatively low resolution. However, the proposed methods are valid for input images with higher resolution, and would perform even better because the image features would have less noise in higher resolution images. In the future work, we will develop algorithms to extract thickness information from higher resolution images, and handle calcifications. Also, before the proposed methods can be applied for clinical applications, more patient image data are needed for training and validation.
5. CONCLUSIONS
We have developed a machine learning based image analysis method to automatically reconstruct the 3D geometries of the aortic valve from 3D CT images. The reconstructed valve geometries were directly used in FE models to simulate aortic valve closure on a patient specific level. The image analysis method is composed of several novel algorithms, including the strategy of image feature extraction to build detectors, the SDL algorithm for building D-SSM, and the LC based algorithm for shape inference. The proposed method was evaluated on clinical 3D CT images, and the results showed a good agreement with human experts. We also showed that by accounting for accurate patient-specific geometries, dynamic leaflet attachment curve motion, and experimentally derived human tissue properties, we were able to predict human aortic valve closure. Since the D-SSM approach is very generic, it may also be used for geometry reconstruction of other objects (e.g. the mitral valve). The proposed method offers great potential to streamline the computational modeling process and enables the development of a pre-operative planning system for valve disease diagnosis and treatment.
Acknowledgments
Research for this project was funded in part by NIH grant R01 HL104080.
APPENDIX
Algorithm-1.
SDL Algorithm Part-1 to build an initial dictionary
|
Repeat the following steps from training cycle 1 to T, and get the output. Input at the current training cycle t : (Dt−1 and Rt − 1 are empty at t = 1) A dictionary from the previous training cycle t − 1 A vector describing the “experience” of the dictionary New training data = [X(1), …, X(n), …, X(N)], each X(n) is a shape in the training set Start:
The corresponding vector is from R̃. |
Algorithm-2.
SDL Algorithm Part-2 to refine the dictionary
|
Repeat the following steps from training cycle 1 to T, and get the output. Input at the current training cycle t : A dictionary from the previous training cycle t−1. D0 is the final output of the SDL Algorithm Part-1. M is the number of shapes, and it does not change in SDL Part-2. A vector describing the “experience” of the dictionary. R0 = [1, …, 1], i.e., every element is 1. New training data X = [X(1), …, X(n), …, X(N)], each X(n) is a shape in the training set. Start:
The updated vector |
Footnotes
CONFLICT OF INTEREST STATEMENT
None.
REFERENCES
- 1.Sun W, Martin C, Pham T. Computational modeling of cardiac valve function and intervention. Annu Rev Biomed Eng. 2014;16:53–76. doi: 10.1146/annurev-bioeng-071813-104517. PubMed PMID: 24819475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Auricchio F, Conti M, Morganti S, Reali A. Simulation of transcatheter aortic valve implantation: a patient-specific finite element approach. Computer methods in biomechanics and biomedical engineering. 2014;17(12):1347–1357. doi: 10.1080/10255842.2012.746676. Epub 2013/02/14. PubMed PMID: 23402555. [DOI] [PubMed] [Google Scholar]
- 3.Capelli C, Bosi GM, Cerri E, Nordmeyer J, Odenwald T, Bonhoeffer P, Migliavacca F, Taylor AM, Schievano S. Patient-specific simulations of transcatheter aortic valve stent implantation. Med Biol Eng Comput. 2012;50(2):183–192. doi: 10.1007/s11517-012-0864-1. [DOI] [PubMed] [Google Scholar]
- 4.Dwyer HA, Matthews PB, Azadani A, Ge L, Guy TS, Tseng EE. Migration forces of transcatheter aortic valves in patients with noncalcific aortic insufficiency. The Journal of thoracic and cardiovascular surgery. 2009;138(5):1227–1233. doi: 10.1016/j.jtcvs.2009.02.057. Epub 2009/09/15. PubMed PMID: 19748632. [DOI] [PubMed] [Google Scholar]
- 5.Morganti S, Conti M, Aiello M, Valentini A, Mazzola A, Reali A, Auricchio F. Simulation of transcatheter aortic valve implantation through patient-specific finite element analysis: two clinical cases. J Biomech. 2014;47(11):2547–2555. doi: 10.1016/j.jbiomech.2014.06.007. Epub 2014/07/08. PubMed PMID: 24998989. [DOI] [PubMed] [Google Scholar]
- 6.Wang Q, Kodali S, Primiano C, Sun W. Simulations of transcatheter aortic valve implantation: implications for aortic root rupture. Biomechanics and modeling in mechanobiology. 2015;14(1):29–38. doi: 10.1007/s10237-014-0583-7. Epub 2014/04/17. PubMed PMID: 24736808; PMCID: Pmc4199942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wang Q, Sirois E, Sun W. Patient-specific modeling of biomechanical interaction in transcatheter aortic valve deployment. J Biomech. 2012;45(11):1965–1971. doi: 10.1016/j.jbiomech.2012.05.008. Epub 2012/06/16. PubMed PMID: 22698832; PMCID: Pmc3392407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Morganti S, Brambilla N, Petronio AS, Reali A, Bedogni F, Auricchio F. Prediction of patient-specific post-operative outcomes of TAVI procedure: The impact of the positioning strategy on valve performance. Journal of Biomechanics. 2015 doi: 10.1016/j.jbiomech.2015.10.048. [DOI] [PubMed] [Google Scholar]
- 9.Jaegere Pd, Santis GD, Rodriguez-Olivares R, Bosmans J, Bruining N, Dezutter T, Rahhab Z, Faquir NE, Collas V, Bosmans B, Verhegghe B, Ren C, Geleinse M, Schultz C, Mieghem Nv, Beule MD, Mortier P. Patient-Specific Computer Modeling to Predict Aortic Regurgitation After Transcatheter Aortic Valve Replacement JACC: Cardiovascular Interventions. 2016;9(5):508–512. doi: 10.1016/j.jcin.2016.01.003. [DOI] [PubMed] [Google Scholar]
- 10.Huang X, Dione DP, Compas C, Papademetris X, Lin B, Bregasi A, Sinusas AJ, Staib L, Duncan JS. Contour tracking in echocardiographic sequences via sparse representation and dictionary learning. Medical Image Analysis. 2014;18(2):253–271. doi: 10.1016/j.media.2013.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhu Y, Papademetris X, Sinusas AJ, Duncan JS. Segmentation of the left ventricle from cardiac MR images using a subject-specific dynamical model. IEEE Transactions on Medical Imaging. 2010;29(3):669–687. doi: 10.1109/TMI.2009.2031063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ecabert O, Peters J, Weese J, editors. Modeling shape variability for full heart segmentation in cardiac computed-tomography images. SPIE Medical Imaging. 2006 [Google Scholar]
- 13.Zheng Y, Barbu A, Georgescu B, Scheuering M, Comaniciu D. Four-chamber heart modeling and automatic segmentation for 3-D cardiac CT volumes using marginal space learning and steerable features. IEEE Transaction on Medical Imaging. 2008;27(11):1668–1681. doi: 10.1109/TMI.2008.2004421. [DOI] [PubMed] [Google Scholar]
- 14.Lorenz C, Berg Jv. A comprehensive shape model of the heart. Medical Image Analysis. 2006;10(4):657–670. doi: 10.1016/j.media.2006.03.004. [DOI] [PubMed] [Google Scholar]
- 15.Lin N, Papademetris X, Sinusas AJ, Duncan JS, editors. Analysis of Left Ventricular Motion Using a General Robust Point Matching Algorithm. Medical Image Computing and Computer Assisted Intervention. 2003 [Google Scholar]
- 16.Schneider RJ, Perrin DP, Vasilyev NV, Marx GR, Nido PJd, Howe RD. itral annulus segmentation from four-dimensional ultrasound using a valve state predictor and constrained optical flow. Medical image analysis. 2012;16(2):497–504. doi: 10.1016/j.media.2011.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zheng Y, John M, Liao R, Nöttling A, Boese J, Kempfert J, Walther T, Brockmann G, Comaniciu D. Automatic aorta segmentation and valve landmark detection in C-arm CT for transcatheter aortic valve implantation. IEEE Transactions on Medical Imaging. 2012;31(12):2307–2321. doi: 10.1109/TMI.2012.2216541. [DOI] [PubMed] [Google Scholar]
- 18.Pouch AM, Wang H, Takabe M, Jackson BM, Sehgal CM, III, JHG, Gorman RC, Yushkevich PA. Automated Segmentation and Geometrical Modeling of the Tricuspid Aortic Valve in 3D Echocardiographic Images. Medical Image Computing and Computer Assisted Intervention. 2013;1:485–492. doi: 10.1007/978-3-642-40811-3_61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ionasec RI, Voigt I, Georgescu B, Wang Y, Houle H, Vega-Higuera F, Navab N, Comaniciu D. Patient-Specific Modeling and Quantification of the Aortic and Mitral Valves From 4-D Cardiac CT and TEE. IEEE Transactions on Medical Imaging. 2010;29(9):1636–1651. doi: 10.1109/TMI.2010.2048756. [DOI] [PubMed] [Google Scholar]
- 20.Palmer RI, Xie X, Tam G, editors. the British Machine Vision Conference (BMVC) BMVA Press; 2015. Automatic Aortic Root Segmentation with Shape Constraints and Mesh Regularisation. [Google Scholar]
- 21.Yang J, Staib L, Duncan JS. Neighbor-constrained segmentation with level set based 3-D deformable models. IEEE Transactions on Medical Imaging. 2004;23(8):940–948. doi: 10.1109/TMI.2004.830802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, Gerigb G. User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. NeuroImage. 2006;31(3):1116–1128. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]
- 23.Freedman DA. Statistical Models: Theory and Practice. Cambridge University Press; 2009. [Google Scholar]
- 24.Wang Q, Book G, Contreras Ortiz S, Primiano C, McKay R, Kodali S, Sun W. Dimensional Analysis of Aortic Root Geometry During Diastole Using 3D Models Reconstructed from Clinical 64-Slice Computed Tomography Images. Cardiovascular Engineering and Technology. 2011;2(4):324–333. [Google Scholar]
- 25.Schievano S, Migliavacca F, Coats L, Khambadkone S, Carminati M, Wilson N, Deanfield JE, Bonhoeffer P, Taylor AM. Percutaneous Pulmonary Valve Implantation Based on Rapid Prototyping of Right Ventricular Outflow Tract and Pulmonary Trunk from MR Data. Radiology. 2007;242(2):490–497. doi: 10.1148/radiol.2422051994. [DOI] [PubMed] [Google Scholar]
- 26.Sun W, Martin C, Pham T. Computational Modeling of Cardiac Valve Function and Intervention. Annual Review of Biomedical Engineering. 2014;16:53–76. doi: 10.1146/annurev-bioeng-071813-104517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Labrosse MR, Beller CJ, Boodhwani M, Hudson C, Sohmer B. Subject-specific finite-element modeling of normal aortic valve biomechanics from 3D+t TEE images. Med Image Anal. 2015;20(1):162–172. doi: 10.1016/j.media.2014.11.003. Epub 2014/12/06. PubMed PMID: 25476416. [DOI] [PubMed] [Google Scholar]
- 28.Botsch M, Kobbelt L, Pauly M, Alliez P, Levy B. Polygon Mesh Processing. A K Peters/CRC Press; 2010. [Google Scholar]
- 29.Yu K, Zhang T, Gong Y. Nonlinear Learning using Local Coordinate Coding. Neural Information Processing Systems. 2009 [Google Scholar]
- 30.Wang J, Yang J, Yu K, Lv F, Huang T, Gong Y. Locality-constrained Linear Coding for Image Classification. Computer Vision and Pattern Recognition. 2010 [Google Scholar]
- 31.Bottou L. Online Algorithms and Stochastic Approximations. Cambridge University Press; 1998. [Google Scholar]
- 32.Devijver PA. Pattern Recognition: A Statistical Approach. London, GB: Prentice-Hall; 1982. [Google Scholar]
- 33.Fan R-E, Chang K-W, Hsieh C-J, Wang X-R, Lin C-J. LIBLINEAR: A library for large linear classification. Journal of Machine Learning Research. 2008;9 [Google Scholar]
- 34.Heimann T, Meinzer H-P. Statistical shape models for 3D medical image segmentation: a review. Medical Image Analysis. 2009;13(4):543–563. doi: 10.1016/j.media.2009.05.004. [DOI] [PubMed] [Google Scholar]
- 35.Martin C, Sun W. Biomechanical characterization of aortic valve tissue in humans and common animal models. Journal of Biomedical Materials Research: Part A. 2012;100A(6):1591–1599. doi: 10.1002/jbm.a.34099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gasser TC, Ogden RW, Holzapfel GA. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J R Soc Interface. 2006;3:15–35. doi: 10.1098/rsif.2005.0073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wang Q, Primiano C, Sun W. Can isolated annular dilatation cause significant ischemic mitral regurgitation? Another look at the causative mechanisms. Journal of Biomechanics. 2014;47(8):1792–1799. doi: 10.1016/j.jbiomech.2014.03.033. [DOI] [PubMed] [Google Scholar]
- 38.Viola P, Jones M. Robust Real-time Object Detection. International Journal of Computer Vision. 2001 [Google Scholar]
- 39.Ciresan D, Giusti A, Gambardella L, Schmidhuber J. Deep Neural Networks Segment Neuronal Membranes in Electron Microscopy Images. Advances in Neural Information Processing Systems. 2012 [Google Scholar]
- 40.Arel I, Rose DC, Karnowski TP. Deep Machine Learning - A New Frontier in Artificial Intelligence Research. IEEE Computational Intelligence Magazine. 2010;5(4):13–18. [Google Scholar]
- 41.Schmidhuber J. Deep Learning in Neural Networks: An Overview. Neural Networks. 2015;61:85–117. doi: 10.1016/j.neunet.2014.09.003. [DOI] [PubMed] [Google Scholar]
- 42.Ghesu FC, Krubasik E, Georgescu B, Singh V, Zheng Y, Hornegger J, Comaniciu D. Marginal Space Deep Learning: Efficient Architecture for Volumetric Image Parsing. IEEE Transactions on Medical Imaging. 2016;35(5):1217–1228. doi: 10.1109/TMI.2016.2538802. [DOI] [PubMed] [Google Scholar]
- 43.Cootes TF, Taylor CJ, Cooper DH, Graham J. Active shape models - their training and application. Computer Vision and Image Understanding. 1995;61:38–59. [Google Scholar]
- 44.Grande KJ, Cochran RP, Reinhall PG, Kunzelma KS. Stress variations in the human aortic root and valve: The role of anatomic asymmetry. Ann Biomed Eng. 1998;26(4):534–545. doi: 10.1114/1.122. [DOI] [PubMed] [Google Scholar]
- 45.Conti CA, Votta E, Della Corte A, Del Viscovo L, Bancone C, Cotrufo M, Redaelli A. Dynamic finite element analysis of the aortic root from MRI-derived parameters. Med Eng Phys. 2010;32(2):212–221. doi: 10.1016/j.medengphy.2009.12.003. Epub 2010/01/12. doi: S1350-4533(09)00264-1 [pii]. PubMed PMID: 20060766. [DOI] [PubMed] [Google Scholar]
- 46.Brewer R, Mentzer R, Deck J, Ritter R, Trefil J, Nolan S. An in vivo study of the dimensional changes of the aortic valve leaflets during the cardiac cycle. Journal of Thoracic and Cardiovascular Surgery. 1977;74:645–650. [PubMed] [Google Scholar]