Personalized Dose Finding Using Outcome Weighted Learning

Abstract

In dose-finding clinical trials, it is becoming increasingly important to account for individual level heterogeneity while searching for optimal doses to ensure an optimal individualized dose rule (IDR) maximizes the expected beneficial clinical outcome for each individual. In this paper, we advocate a randomized trial design where candidate dose levels assigned to study subjects are randomly chosen from a continuous distribution within a safe range. To estimate the optimal IDR using such data, we propose an outcome weighted learning method based on a nonconvex loss function, which can be solved efficiently using a difference of convex functions algorithm. The consistency and convergence rate for the estimated IDR are derived, and its small-sample performance is evaluated via simulation studies. We demonstrate that the proposed method outperforms competing approaches. Finally, we illustrate this method using data from a cohort study for Warfarin (an anti-thrombotic drug) dosing.

1 Introduction

Dose finding plays an important role in clinical trials, which aim to assess drug toxicity, identify maximum tolerated doses for safety, and determine drug efficacy, while at the same time recognizing the potential that overdosing can increase the risk of side effects and underdosing can diminish the effects of the therapeutic drug. A typical design for dose finding trials is a double-blinded Phase II trial that is conducted to identify the no-effect, the mean effective, and the maximal effective doses (Chevret, 2006). In such trials, patients are randomized to a few fixed safe dose levels for a candidate drug. A single dose level is usually determined by comparing the average outcome of each dose level and then extrapolating for future recommendations. However, this one-size-fits-all approach is not optimal when treatment responses to the drug are heterogeneous among patients, since what works for some patients may not necessarily work for others. Hence, personalized treatment, which tailors drug dose levels according to individual health conditions and disease prognosis, is desirable. Furthermore, the flexibility of using continuous individualized dose levels can help improve clinical practice and increase a patient’s compliance. For example, it is widely known that Warfarin, a common drug for the prevention of thrombosis and thromboembolism, is administered in varying doses, ranging from 10mg to 100mg per week depending on the patient’s individual clinical and genetic factors (The International Warfarin Pharmacogenetics Consortium, 2009).

As the future of personalized medicine continues to gain prominence as a vital mechanism for the effective treatment of multiple diseases and conditions, there is a growing amount of literature dedicated to the development of study designs and methods for personalized treatment, yet these approaches remain restricted to a finite number of options. A randomized trial design, where the finite treatment options are randomly assigned to patients, is the most valid design to estimate the optimal individualized treatment rule (ITR), which is the treatment decision rule determined by a patient’s pre-treatment condition that aims to maximize the expected beneficial clinical outcome, also known as the reward. To infer the ITR using data from such a trial, earlier work has proposed certain parametric or semiparametric models to group patients into subgroups according to their risk levels (Eagle et al., 2004; Marlowe et al., 2007; Cai et al., 2010). However, the parametric/semiparametric model assumption is likely to be invalid due to the complexity of disease mechanisms and individual heterogeneity. More recently, the literature has proposed the use of powerful statistical learning methods, which perform well in analyzing data with high complexity and can be categorized into two groups, namely indirect methods and direct methods. The most popular indirect method is called Q-learning, which is essentially a two-step regression-based approach (Qian and Murphy, 2011; Chakraborty and Moodie, 2013; Moodie et al., 2014; Zhao et al., 2009). Its first step consists of fitting a regression model for the conditional expectation of the reward given the treatments, covariates, and the treatment-covariate interactions. The regression model can be either a parametric regression with complexity penalization, such as LASSO, or a nonparametric learning method, such as a regression tree (Breiman et al., 1984) or support vector regression (SVR, Vapnik (1995); Smola and Schölkopf (2004)). In the second step, the optimal treatment for a given covariate value is obtained as the treatment option that maximizes the predicted mean reward estimated from the regression model in the first step. Some alternative regression-based methods based on regret or contrasts between treatment responses have also been suggested for the first step (Robins, 2004; Moodie et al., 2009; Henderson et al., 2010; Schulte et al., 2014; Wallace and Moodie, 2015), which are equivalent to Q-learning in a randomized trial setting (Schulte et al., 2014).

In regards to the potential over-fitting in the first step of Q-learning, which can lead to a less than optimal ITR, direct methods have been proposed by Zhao et al. (2012). Specifically, Zhao et al. (2012) introduced the framework of outcome weighted learning (O-learning) to directly find the optimal binary treatment rule, where the problem of finding the optimal ITR is formulated as a weighted binary classification with the rewards as weights. The authors demonstrated superior performance of O-learning over indirect methods especially when the sample size is small, which is not uncommon in clinical trials. In other relevant work, Zhang et al. (2012a,b) proposed a robust semiparametric regression function for maximization to infer the optimal rule; comparatively, the O-learning approach in Zhao et al. (2012) is more robust and can handle higher dimensional covariates.

Extending the current designs and methods to personalized dose finding is not trivial because there can be an infinite number of treatment options per a given interval. To infer the optimal individualized dose rule (IDR), a good design should ensure each candidate dose level has a potential chance to be observed in the trial and the different outcomes from patients receiving different dose levels should only be attributed to dose level difference. Therefore, a randomized dose trial design, where each patient receives a dose level randomly chosen from a continuous distribution within the range of safe doses, should be adopted. Indeed, we will show that such a design can lead to a consistent optimal IDR asymptotically.

When analyzing data from such a design, the existing methods for handling finite treatment options can no longer be applied. First, for Q-learning, the performance can be sensitive to the regression model specification in the first step. To identify the IDR, both the main and interaction effect of a continuous dose variable and many covariates on the reward need to be correctly specified. Furthermore, since the regression model in the first step has a high potential for nonlinear interactions, the optimization in the second step will be a nonlinear optimization problem for each given set of covariate values, which can be very unstable and computationally intensive when the dimension of covariates is not small. On the other hand, existing direct methods, including for example outcome weighted learning, which maximizes the value associated with each IDR by using patients whose dose assignment follows this rule, are not applicable since only a few patients are likely to be given the dose level specified by the rule for each covariate value. This is because the dose level follows a continuous distribution, so that the probability of observing a dose equal to the rule-specified dose is zero. We will further elaborate on this in the next section.

In this paper, we advocate the randomized trial design for personalized dose finding and show that this design leads to a consistent optimal IDR. Using data from such a design, we propose a robust outcome weighted learning method to infer the optimal IDR. Our proposed method is a non-trivial extension of O-learning for binary treatments proposed by Zhao et al. (2012). Specifically, we show that the dose finding problem is a weighted regression with individual rewards as weights. We then propose a nonconvex loss function for optimization, and provide a difference of convex functions (DC) algorithm to solve the corresponding optimization problem. We show that this loss function can lead to consistent estimation of the optimal dose. As far as we know, this is the first direct method for estimating IDR where treatment options are on a continuum.

The outline of the rest of the paper is as follows: In Section 2, we first introduce appropriate background information on IDRs and provide an overview of O-learning for binary treatment options. We then discuss how to extend O-learning for estimating an optimal IDR using data from a randomized dose trial, such that there is no unmeasured confounding. Section 3 describes the DC algorithm for solving the optimization problem. The theoretical properties of our method are provided in Section 4. Since existing data comes mostly from observational studies, we extend our approach to analyze such data in Section 5. In Section 6, we demonstrate through simulation studies that our proposed method can identify optimal IDRs which lead to a better predicted clinical outcome than competing methods. In Section 7, the proposed method is applied to analyzing data from a Warfarin study. A concluding discussion is given in Section 8. Most of the proofs are deferred to the Appendix. Sample simulation codes are included as the web supplementary file.

2 Method

2.1 Individualized Dose Rule

As previously mentioned, we consider a randomized dose trial where each patient receives a dose level randomly selected from a continuous distribution in an interval within a safe dose range. Particularly, this assignment can be achieved using a random number generator. Thus, we assume the data are collected from a randomized trial with dose assignment A, which could have many dose levels even in this finite sample, and we assume patient-level covariates consist of a d-dimensional vector X = (X₁, X₂, …, X_d)^T ∈ 𝒳. The traditional dose finding trial is usually designed to identify the best dose level among some small number of fixed dose levels. In contrast, we allow A to be continuous over a bounded interval 𝒜 (a safe dose range). Without loss of generality, we assume that 𝒜 = [0, 1]. The clinical beneficial outcome, the reward, is denoted as R and assumed to be bounded and positive. An IDR is a map f : 𝒳 → 𝒜 that outputs a dose suggestion based on a patient’s covariate value. A value function corresponding to this IDR, as denoted by 𝒱(f), is defined as the expected reward in the population if the dose levels for the subjects follow the rule f, i.e., A = f(X). Specifically, if we let R^*(a) be the outcome that would be observed if the dose level a were given, then 𝒱(f) = E[R^*(f(X))].

We assume the Stable Unite Treatment Value Assumption (SUTVA) (see Rubin (1978)). That is, R = Σ_a I(A = a)R^*(a). Then under a randomized dose design, since A is independent of R^*(a) given X, we obtain

$$\begin{array}{l}\mathcal{V}(f)=E[R^{\ast }(f(\mathbf{X}))]\\ =E_{\mathbf{X}}[E\{R^{\ast }(f(\mathbf{X}))\mid \mathbf{X}\}]=E_{\mathbf{X}}[E\{R^{\ast }(f(\mathbf{X}))\mid A=f(\mathbf{X}),\mathbf{X}\}]\\ =E_{\mathbf{X}}[E\{R\mid A=f(\mathbf{X}),\mathbf{X}\}].\end{array}$$ (1)

As a result, the optimal rule f_opt = argmax_f𝒱(f). Note that f_opt does not change if R is replaced by R + g(X) for any known function g(X) (a common choice of g(X) is a constant function). Also, f_opt is invariant in the scale of R. Thus, without loss of generality, we assume that R is positive by subtracting from R its lower bound.

Therefore, we conclude that for any IDR f, 𝒱(f) can be estimated consistently using the mean of the reward among subjects whose dose levels are the same as f(X). In other words, a randomized dose design can consistently evaluate the values from all IDRs to lead to a consistent optimal IDR when the sample size is large enough. This justifies the use of such a design in personalized dose finding.

2.2 O-learning for personalized dose finding

In this section, we propose a learning method to estimate f_opt using data from a randomized dose trial which consist of n observations (A_i, X_i, R_i), i = 1, …, n. The essential idea is to use empirical data to estimate 𝒱(f) then directly optimize this estimated function for f_opt. Specifically, we extend the O-learning method in Zhao et al. (2012) for binary treatment options to our setting, but with non-trivial modifications.

When A is a binary treatment, both Qian and Murphy (2011) and Zhao et al. (2012) show that 𝒱(f) is equal to E[RI(A = f(X))/p(A|X)], where p(a|X) is the randomization probability of A = a given X. Therefore, 𝒱(f) can be empirically approximated by $n^{-1}{\sum }_{i=1}^n{R}_{i}I(A_i=f({\mathbf{X}}_i))/p(A_i\mid {\mathbf{X}}_i)$. Thus, estimating f_opt can be carried out by maximizing the above function, which is also equivalent to minimizing

$${\mathcal{R}}_n(f)=n^{-1}\sum _{i=1}^n{R}_{i}I(A_i\ne f({\mathbf{X}}_i))/p(A_i\mid {\mathbf{X}}_i).$$

However, since minimizing this function is infeasible due to the discontinuity of the indicator function, the O-learning method in Zhao et al. (2012) proposes to minimize a surrogate version of the above loss function by replacing the indicator function with a hinge loss function defined as

$$n^{-1}\sum _{i=1}^n{R}_{i}I{(1-A_{i}f({\mathbf{X}}_i))}_{+}/p(A_i\mid {\mathbf{X}}_i)+{\lambda }_n{\Vert f\Vert }^2,$$

where x₊ = max(x, 0), ||f|| is the seminorm for f from a normed space (usually, a reproducing kernel Hilbert space) and λ_n is a tuning parameter. Equivalently, O-learning is a weighted version of a support vector machine (SVM), where each subject is weighted by his/her reward value R_i. For the binary treatment options, this minimization leads to a consistent optimal treatment rule.

Direct adaption of O-learning to our dose finding setting is not feasible when A is continuous. First, the probability p(A|X) is always zero since A is continuous. Second, in the empirical approximation to 𝒱(f) in O-learning, only a few subjects satisfy A_i = f(X_i), so this approximation is very unstable. On the other hand, it may be tempting to modify ℛ_n(f) to resolve these two issues by replacing p(A_i|X_i) with the density function of A_i given X_i and replacing I(A_i ≠ f(X_i)) with a smooth loss, such as (A_i − f(X_i))² or |A_i − f(X_i)|. However, our Lemma 1 in the Appendix shows that the estimated dose rule resulting from such a loss is not consistent for the optimal IDR. Therefore, this motivates us to find a different approximation to 𝒱(f) as detailed in the following.

First, assuming E[R|A = a, X] to be continuous in a, we note that

$$\underset{\varphi \to 0+}{lim}\frac{E[RI[A\in (a-\varphi ,a+\varphi )]/p(A\mid \mathbf{X})\mid \mathbf{X}]}{2\varphi }=E[R\mid A=a,\mathbf{X}],$$

where p(a|X) is the conditional density of A = a given X, which is known and positive by design. As a result,

$$\begin{array}{l}\underset{\varphi \to 0^{+}}{lim}E\left\{\frac{RI[A\in (f(\mathbf{X})-\varphi ,f(\mathbf{X})+\varphi )]}{2\varphi p(A\mid \mathbf{X})}\right\}=E_{\mathbf{X}}[E\{R\mid A=f(\mathbf{X}),\mathbf{X}\}]\\ =\mathcal{V}(f).\end{array}$$

If we let

$${\stackrel{\sim }{\mathcal{V}}}_{\varphi }(f)=E\left[\frac{RI[A\in (f(\mathbf{X})-\varphi ,f(\mathbf{X})+\varphi )]}{2\varphi p(A\mid \mathbf{X})}\right],$$

then 𝒱̃_ϕ(f) approximates 𝒱(f) when ϕ is sufficiently small. Hence, an IDR maximizing 𝒱̃_ϕ(f), or equivalently, minimizing

$$E\left[\frac{R}{2\varphi p(A\mid \mathbf{X})}\right]-{\stackrel{\sim }{\mathcal{V}}}_{\varphi }(f)=E\left[\frac{RI(\mid A-f(\mathbf{X})\mid >\varphi )]}{2\varphi p(A\mid \mathbf{X})}\right],$$ (2)

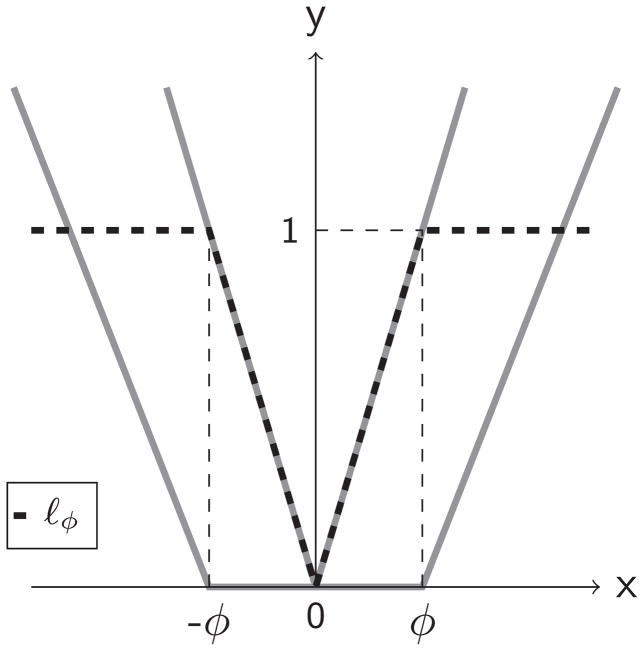
will be close to the optimal IDR. The zero-one loss I(|A − f(X)| > ϕ) in the expression often causes difficulty when optimizing using empirical data (Zhang, 2004). Thus, a continuous surrogate loss to replace the zero-one loss is more desirable. Specifically, in our method, we choose such a surrogate loss to be

$${\ell }_{\varphi }(A-f(\mathbf{X}))=min\left(\frac{\mid A-f(\mathbf{X})\mid }{\varphi },1\right).$$

Note that ℓ_ϕ(x) is the difference of two convex functions |x|/ϕ and (x/ϕ − 1)₊. Figure 1 plots the curve of ℓ_ϕ(x) and these two convex functions. Clearly, when ϕ goes to zero, ℓ_ϕ(x) converges to the indicator function I(x ≠ 0). After replacing the zero-one loss by the new surrogate loss in (2), the objective function to be minimized for the optimal IDR becomes

Figure 1.

Loss function ℓ_ϕ for dose finding in an IDR. ℓ_ϕ (black, dash) is the difference between the V shaped function (gray, solid) and U shaped function (gray, solid).

$${\mathcal{R}}_{\varphi }(f)=E\left[\frac{R{\ell }_{\varphi }(A-f(\mathbf{X}))}{\varphi p(A\mid \mathbf{X})}\right],$$

and the counterpart to 𝒱̃_ϕ(f) is

$$V_{\varphi }(f)=E\left[\frac{R}{\varphi p(A\mid \mathbf{X})}\right]-{\mathcal{R}}_{\varphi }(f)=E\left[\frac{Rmax(1-\mid A-f(\mathbf{X})\mid /\varphi ,0)}{\varphi p(A\mid \mathbf{X})}\right].$$

Finally, using the data from a randomized dose trial, we propose to minimize the empirical version of ℛ_ϕn(f) for some constant ϕ_n, which will be chosen data adaptively, denoted by

$${\widehat{\mathcal{R}}}_{{\varphi }_n}(f)=\frac{1}{n}\sum _{i=1}^n\frac{R_i{\ell }_{{\varphi }_n}[A_i-f({\mathbf{X}}_i)]}{{\varphi }_{n}p(A_i\mid {\mathbf{X}}_i)},$$

to estimate the optima IDR. Furthermore, to prevent overfitting, we penalize the complexity of f(X) as in the standard support vector machine. Consequently, our O-learning method solves the following optimization problem:

$$\underset{f}{min}\left\{\frac{1}{n}\sum _{i=1}^n\frac{R_i{\ell }_{{\varphi }_n}(A_i-f({\mathbf{X}}_i))}{2{\varphi }_{n}p(A_i\mid {\mathbf{X}}_i)}+{\lambda }_n{\Vert f\Vert }^2\right\},$$ (3)

where ||f|| is some seminorm for f, and λ_n controls the severity of the penalty on f. For example, if we assume a linear decision rule, f(X) = X^Tw + b and ||f|| is the Euclidean norm of w, kernel tricks can be used to obtain a nonlinear rule by assuming f is from a reproducing kernel Hilbert space and || · || is the corresponding norm.

3 Computational Algorithm

The objective function in (3) is nonconvex, and nonconvex optimization is known to be difficult. However, noting that ℓ_ϕ is the difference of the two convex functions defined earlier, we will adapt the difference of convex functions (DC) algorithm (An and Tao, 1997) to tackle this nonconvex optimization. We first discuss the algorithm for the linear learning rule, where f(X) is a linear function of X, and then extend it to a nonlinear learning rule where f(X) is chosen from a Reproducing Kernel Hilbert Space (RKHS).

3.1 Learning a linear IDR

Consider f(X) = X^Tw + b. To simplify the notation, we absorb the p(A|X) into R, as p(A|X) is known in a randomized trial. We can formulate the objective function as follows:

$$S(\mathbf{\Theta })=\frac{{\lambda }_n}{2}\Vert \mathbf{w}{\Vert }_2^2+\frac{1}{n{\varphi }_n}\sum _{i=1}^n{R}_{i}min(\frac{\mid A_i-({\mathbf{X}}_i^T\mathbf{w}+b)\mid }{{\varphi }_n},1),$$

where λ_n is the tuning parameter and Θ = (w^T, b)^T. From Figure 1, we express the objective function S as the difference of two convex functions, S(Θ) = S₁(Θ) − S₂(Θ), where

$$S_1(\mathbf{\Theta })=(\frac{{\lambda }_n}{2}\Vert \mathbf{w}{\Vert }_2^2+\frac{1}{n{\varphi }_n}\sum _{i=1}^n{R}_i\frac{\mid A_i-({\mathbf{X}}_i^T\mathbf{w}+b)\mid }{{\varphi }_n})$$

and

$$S_2(\mathbf{\Theta })=\frac{1}{n{\varphi }_n}\sum _{i=1}^n{R}_i{(\frac{\mid A_i-({\mathbf{X}}_i^T\mathbf{w}+b)\mid }{{\varphi }_n}-1)}_{+}.$$

Then, the DC algorithm is essentially an iterative sequence of convex minimization problems for solving the original nonconvex minimization problem. Specifically, we initialize Θ⁰, then repeatedly update Θ via

$${\mathbf{\Theta }}^{t+1}={\text{argmin}}_{\mathbf{\Theta }}(S_1(\mathbf{\Theta })-{[\nabla S_2({\mathbf{\Theta }}^t)]}^T(\mathbf{\Theta }-{\mathbf{\Theta }}^t))$$

until convergence of Θ, where ∇S₂(Θ^t) is the gradient function of S₂(Θ) evaluated at Θ^t. For the initial value of Θ, we use a least squares estimator to predict A with X as predictors using the observations with a large observed reward, e.g. the observations with R_i in the upper 50th percentile of the training data.

The minimization step to obtain Θ^t+1 is a convex minimization, which we will detail in the following. In this step, if we define $Q_i^{(t)}=I(\mid a_i-{\mathbf{X}}_i^T{\mathbf{w}}^t-b^t\mid \le {\varphi }_n)$, where ${\mathbf{X}}_i^T{\mathbf{w}}^t+b^t$ is the temporary predicted optimal dose with w^t and b^t being the solution from the t-th iteration, then after some algebra, the objective function for this step, denoted by S^(t+1)(Θ), equals

$$\frac{{\lambda }_n}{2}\Vert \mathbf{w}{\Vert }_2^2+\frac{1}{n{\varphi }_n^2}\sum _{i=1}^n{R}_i{Q}_i^{(t)}\mid a_i-{\mathbf{X}}_i^T\mathbf{w}-b\mid .$$

Consequently, the convex subproblem is a weighted penalized median regression problem. Note that the t-th iteration result only impacts S^t+1 through $Q_i^t$. Thus, if the observed patient receives a dose that is close to the surrogate optimal dose ( $Q_i^{(t)}=1$), then that observation will contribute to the objective function of the t + 1 step subproblem, otherwise it will not contribute. Let $\mathcal{T}=\{i:Q_i^{(t)}=1\}$. Divide the objective function by λ_n and introduce slack variables into S^(t+1)(Θ); then the primary optimization problem at the t+1-th iteration becomes

$$\underset{\mathbf{w},b,\xi ,\stackrel{\sim }{\xi }}{min}\frac{1}{2}\Vert \mathbf{w}{\Vert }_2^2+\frac{1}{n{\lambda }_n{\varphi }_n^2}\sum _{i\in \mathcal{T}}({\xi }_i+{\stackrel{\sim }{\xi }}_i)R_i,$$ (4)

subject to ξ_i, ξ̃_i ≥ 0, $a_i-{\mathbf{X}}_i^T\mathbf{w}-b\le {\xi }_i,-(a_i-{\mathbf{X}}_i^T\mathbf{w}-b)\le {\stackrel{\sim }{\xi }}_i$, ∀i ∈ 𝒯. Using Lagrangian multipliers and employing some algebra, we end up minimizing

$$\begin{array}{c}\frac{1}{2}\Vert \mathbf{w}{\Vert }_2^2+\frac{1}{n{\lambda }_n{\varphi }_n^2}\sum _{i\in \mathcal{T}}({\xi }_i+{\stackrel{\sim }{\xi }}_i)R_i-\sum _{i\in \mathcal{T}}{\alpha }_i({\xi }_i-a_i+{\mathbf{X}}_i^T\mathbf{w}+b)\\ -\sum _{i\in \mathcal{T}}{\stackrel{\sim }{\alpha }}_i({\stackrel{\sim }{\xi }}_i+{\alpha }_i-{\mathbf{X}}_i^T\mathbf{w}-b)-\sum _{i\in \mathcal{T}}{u}_i{\xi }_i-\sum _{i\in \mathcal{T}}{\stackrel{\sim }{u}}_i{\stackrel{\sim }{\xi }}_i\end{array}$$

subject to

$$\begin{array}{c}\mathbf{w}-\sum _{i\in \mathcal{T}}{\alpha }_i{\mathbf{X}}_i+\sum _{i\in \mathcal{T}}{\stackrel{\sim }{\alpha }}_i{\mathbf{X}}_i=0;-\sum _{i\in \mathcal{T}}{\alpha }_i+\sum _{i\in \mathcal{T}}{\stackrel{\sim }{\alpha }}_i=0;\\ \frac{R_i}{n{\lambda }_n{\varphi }_n^2}-{\alpha }_i-u_i=0;\frac{R_i}{n{\lambda }_n{\varphi }_n^2}-{\stackrel{\sim }{\alpha }}_i-{\stackrel{\sim }{u}}_i=0.\end{array}$$

After plugging in the equations obtained from the above constraints, we obtain the following convex dual problem:

$$\underset{\alpha ,\stackrel{\sim }{\alpha }}{min}\frac{1}{2}\sum _{i\in \mathcal{T}}\sum _{j\in \mathcal{T}}({\alpha }_i-{\stackrel{\sim }{\alpha }}_i)\langle {\mathbf{X}}_i,{\mathbf{X}}_j\rangle ({\alpha }_j-{\stackrel{\sim }{\alpha }}_j)-\sum _{i\in \mathcal{T}}({\alpha }_i-{\stackrel{\sim }{\alpha }}_i)a_i$$

subject to

$$\sum _{i\in \mathcal{T}}({\alpha }_i-{\stackrel{\sim }{\alpha }}_i)=0;0\le {\alpha }_i\le \frac{R_i}{n{\lambda }_n{\varphi }_n^2},0\le {\stackrel{\sim }{\alpha }}_i\le \frac{R_i}{n{\lambda }_n{\varphi }_n^2},\forall i\in \mathcal{T},$$

where 〈·, ·〉 denotes inner product, i.e. ${\mathbf{X}}_i^T{\mathbf{X}}_j$. This dual problem is a quadratic programming (QP) problem and is solvable via many standard optimization packages. Once its solution is obtained, the coefficients w can be recovered by the relation w = Σ_i∈𝒯(α_i − α̃_i)X_i. After the solution of w is derived, b can be obtained by solving either a sequence of Karush-Kuhn-Tucker conditions or linear programming (Boyd and Vandenberghe, 2004).

In the DC algorithm, the iterations stop when ||w^t+1 − w^t|| is smaller than a pre-specified small constant (10⁻⁸ in our simulations). Note that since the convex function S₂(Θ) is replaced by its affine majorization, the DC algorithm is also a special case of the minorize-maximize or majorize-minimize (MM) algorithm (Hunter and Lange, 2004). Additionally, the objective function S(Θ) is bounded below by 0, and S^(t) is descending after each iteration, and it is thus guaranteed that the DC algorithm converges to a local minimizer in finite steps (An and Tao, 1997).

3.2 Learning a nonlinear IDR

To allow more flexible functional forms for the decision, we define the kernel K(·, ·) as a symmetric, continuous and positive semidefinite function mapping from 𝒳 × 𝒳 to ℝ. A Reproducing Kernel Hilbert Space (RKHS) H_K associated with K is the completion of the linear span of all functions K(·, X), X ∈ 𝒳. In addition, there always exists a transform of X, Φ(·) such that Φ(X_i)^T Φ(X_j) = K(X_i, X_j). We further assume that the decision function for optimal dose f(X) is from H_K, i.e., f(X) = w^T Φ(X) + b (Vapnik (1995); Smola and Schölkopf (2004)). Using similar derivations to that done in the linear learning setting, we obtain the following dual problem for nonlinear learning:

$$\underset{\alpha ,\stackrel{\sim }{\alpha }}{min}\frac{1}{2}\sum _{i\in \mathcal{T}}\sum _{j\in \mathcal{T}}({\alpha }_i-{\stackrel{\sim }{\alpha }}_i)K({\mathbf{X}}_i,{\mathbf{X}}_j)({\alpha }_j-{\stackrel{\sim }{\alpha }}_j)-\sum _{i\in \mathcal{T}}({\alpha }_i-{\stackrel{\sim }{\alpha }}_i)a_i$$

subject to

$$\sum _{i\in \mathcal{T}}({\alpha }_i-{\stackrel{\sim }{\alpha }}_i)=0;0\le {\alpha }_i\le \frac{R_i}{n{\lambda }_n{\varphi }_n^2},0\le {\stackrel{\sim }{\alpha }}_i\le \frac{R_i}{n{\lambda }_n{\varphi }_n^2},\forall i\in \mathcal{T}.$$

After solving the above QP problem, we can recover the coefficients w via

$$\mathbf{w}=\sum _{i=1}^{n}I(i\in \mathcal{T})({\alpha }_i-{\stackrel{\sim }{\alpha }}_i).$$

Then we obtain the intercept b using the same methods as in Section 3.1. According to the representation theorem of Kimeldorf and Wahba (1971), we obtain that at each iteration $f(\mathbf{X})={\sum }_{i=1}^{n}I(i\in \mathcal{T})({\alpha }_i-{\stackrel{\sim }{\alpha }}_i)K(\mathbf{X},{\mathbf{X}}_i)+b$. In our paper, we implement nonlinear learning via the Gaussian kernel, i.e. $K({\mathbf{X}}_i,{\mathbf{X}}_j)=exp(-{\gamma }^{-2}\Vert {\mathbf{X}}_i-{\mathbf{X}}_j{\Vert }_2^2)$, where γ > 0 is the parameter for K(., .). We denote the RKHS induced by the Gaussian kernel as H_γ.

3.3 Tuning parameter selection

We choose the tuning parameters by cross validation. Ideally, we wish to find an unbiased estimate for the true value function so that one can use it to evaluate the prediction performance associated with each tuning parameter using tuning data. However, since the true value function, 𝒱(f), cannot be well estimated in the current setting with continuous dose levels, we suggest the use of an approximate estimate 𝒱_ε(f) where ε is a very small parameter as the criterion function (we set ε = 0.01 in our numerical studies). Therefore, we propose the following procedure for tuning ϕ_n: We divide the data into training and tuning sets and consider a sequence of candidate values for ϕ_n, say Φ = {0.4, 0.35, 0.3, 0.25, 0.2, 0.15, 0.1, 0.05}. For each ϕ_n, we estimate the optimal IDR, denoted by f̂_ϕn, using the training data where λ_n is selected using another cross-validation with the training data only. We then evaluate the predicted value function as the empirical estimate of 𝒱_ε (f̂_ϕn) using the tuning data. Then, the optimal choice of ϕ_n is the one maximizing the average of the predicted values across all the tuning sets.

4 Theoretical Results

In this section, we study the asymptotic behavior of the minimizer (f̂_n), which solves the optimization problem (3). In particular, we will show that 𝒱(f̂_n) converges to 𝒱(f_opt) with a certain rate. This result implies that the estimated rule is an optimal rule asymptotically. As an interesting supplement to this argument, we prove in the Appendix that it is not appropriate to use convex losses, such as least squares loss or absolute deviations loss, to replace the nonconvex loss ℓ_ϕ under the O-learning framework. Our first result shows that our approximation of the value function is valid.

Theorem 1

For any measurable function f : 𝒳 → ℝ, if sup_{(a,x)∈𝒜×𝒳} |∂E(R|A = a,X = x)/∂a| ≤ C for a bounded constant C, then |𝒱_ϕ(f) − 𝒱(f)| ≤ Cϕ_n.

Proof

First, we have

$$\begin{array}{l}{\mathcal{V}}_{\varphi }(f)=E\left\{\frac{R}{{\varphi }_{n}p(A\mid \mathbf{X})}max(1-\frac{\mid A-f(\mathbf{x})\mid }{{\varphi }_n},0)\right\}\\ =E_{\mathbf{X}}\left\{\frac{1}{{\varphi }_n^2}{\int }_{\mid f(x)-a\mid \le {\varphi }_n}[{\varphi }_n-\mid a-f(x)\mid ]E(R\mid A=a,\mathbf{X}=\mathbf{x})da\right\}\\ =E_{\mathbf{X}}\left\{\frac{1}{{\varphi }_n^2}{\int }_{\mid z\mid \le {\varphi }_n}[{\varphi }_n-\mid z\mid ]E(R\mid A=z+f(\mathbf{x}),\mathbf{X}=\mathbf{x})dz\right\}.\end{array}$$

After Taylor expansion, we obtain

$$\begin{array}{l}{\mathcal{V}}_{\varphi }(f)=E_{\mathbf{X}}\left\{\frac{1}{{\varphi }_n^2}{\int }_{\mid z\mid \le {\varphi }_n}[{\varphi }_n-\mid z\mid ]\left[E(R\mid A=a,\mathbf{X}=\mathbf{x})+{z\frac{\partial E(R\mid A=a,\mathbf{X}=\mathbf{x})}{\partial a}|}_{a=f(\mathbf{x})}+o(z)\right]dz\right\}.\\ =V(f)+E_{\mathbf{X}}\left\{\frac{1}{{\varphi }_n^2}{\int }_{\mid z\mid \le {\varphi }_n}[{\varphi }_n-\mid z\mid ]\left[{z\frac{\partial E(R\mid A=a,\mathbf{X}=\mathbf{x})}{\partial a}|}_{a=f(\mathbf{x})}+o(z)\right]dz\right\}.\end{array}$$

Therefore,

$$\mid {\mathcal{V}}_{\varphi }(f)-\mathcal{V}(f)\mid =\left|E_{\mathbf{X}}\left\{\frac{1}{{\varphi }_n^2}{\int }_{\mid z\mid \le {\varphi }_n}[{\varphi }_n-\mid z\mid ]\left[{z\frac{\partial E(R\mid A=a,\mathbf{X}=\mathbf{x})}{\partial a}|}_{a=f(\mathbf{x})}+o(z)\right]dz\right\}\right|.$$

By the condition in Theorem 1, we conclude that

$$\mid {\mathcal{V}}_{\varphi }(f)-\mathcal{V}(f)\mid \le C{\int }_{\mid z\mid \le {\varphi }_n}\frac{{\varphi }_n\mid z\mid -z^2}{{\varphi }_n^2}dz=C{\varphi }_n.$$

The theorem thus holds.

Assume that the kernel function in the reproducing kernel Hilbert space in (3) is a Gaussian kernel. Then our main result establishes the convergence rate of 𝒱(f̂_n) − 𝒱(f_opt), as given in the following theorem.

Theorem 2

Assume that the optimal rule $f_{\mathit{opt}}\in B_{1,\infty }^{\alpha }({ℝ}^d)$, a Besov space, i.e. $B_{1,\infty }^{\alpha }({ℝ}^d)=\{f\in L_{\infty }(({ℝ}^d)):{\mathit{sup}}_{t>0}(t^{-\alpha }{\omega }_{r,L_1(({ℝ}^d))}(f,t))<\infty \}$, where ω is the modulus of continuity. Then, for any ε > 0, d/(d + τ) < p < 1, τ > 0, and parameter γ_n for the Gaussian kernel,

$$\mathcal{V}(f_{\mathit{opt}})-\mathcal{V}({\widehat{f}}_n)\le c_1{\left[\frac{1}{{\gamma }_n^{(1-p)(1+\epsilon )d}{\lambda }_n^p{\varphi }_n^{2}n}\right]}^{\frac{1}{2-p}}+c_2\frac{{\tau }^{1/2}}{{\varphi }_n{n}^{1/2}}+c_3\frac{\tau }{{\varphi }_{n}n}+c_4\frac{{\lambda }_n}{{\gamma }_n^d}+c_5\frac{{\gamma }_n^{\alpha }}{{\varphi }_n^2}+c_6{\varphi }_n$$

with probability P_n not less than 1 − 3e^−τ. The constants c₁ to c₆ are independent of n.

With properly chosen parameters γ_n, λ_n, ϕ_n, the right hand side of the inequality will go to 0 as n goes to infinity. The last term is due to the use of 𝒱_ϕ to approximate 𝒱. The other terms are from the approximation error due to H_γ and the stochastic error due to the finite sample size. We can choose λ_n, γ_n, and ϕ_n to balance the approximation accuracy and the stochastic variability as follows:

$${\lambda }_n={\left(\frac{1}{n}\right)}^{1/4},{\gamma }_n={\left(\frac{1}{n}\right)}^{\frac{3/\alpha }{4+3d/\alpha }},{\varphi }_n={\left(\frac{1}{n}\right)}^{\frac{1}{4+3d/\alpha }}.$$

Then, the optimal rate for the value function approximation using the estimated rule is

$$\mathcal{V}(f_{\mathit{opt}})-\mathcal{V}({\widehat{f}}_n)=O_p\left({\left(\frac{1}{n}\right)}^{\frac{1}{4+3d/\alpha }}\right).$$

Theorem 2 implies that the value of the estimated rule f̂_n from O-learning converges to the optimal value function. Clearly, the convergence rate decreases as the dimension of prognostic variables increases. Moreover, if f_opt is smooth enough, i.e. α goes to infinity, the optimal convergence rate of O-learning with Gaussian kernel is close to the rate n^−1/4. Note that the rate cannot be close to n⁻¹, the rate proved by Zhao et al. (2012) for a binary treatment rule. The main reason is due to the continuous nature of the dose, i.e. the data used for learning are only from subjects who have received similar dose levels.

5 Extension to Observational Studies

In the above development, we assumed that the training data was from a randomized dose trial. However, in practice, the training data can also come from observational data, where the distribution of receiving a particular dose given the covariates is unknown and therefore needs to be estimated. More importantly, similar to causal inference using observational data, we make the no unobserved confounders assumption. That is, conditional on all covariates X, the observed dose level, A, is independent of all potential outcomes R^*(a). Under this assumption, the proposed O-learning approach remains valid except that the density p(a|X) needs to be estimated by the observed data.

A simple approach to estimate p(a|X) is based on some parametric model, for example, the logarithm of the observed dose follows a normal distribution with mean as a linear function of the covariates and splines of the covariates (Imai and Van Dyk, 2004). In addition, more nonparametric methods such as boosting (Bühlmann and Hothorn, 2007; Zhu et al., 2015), Random Forests (Breiman, 2001), and SVR can be used to estimate the mean function in the above model. In our numerical studies, we will utilize the latter to estimate the mean of the normal distribution for the logarithm of A given X.

6 Simulation Study

6.1 Simulation for a randomized trial

We have conducted extensive simulations to assess the performance of the proposed method with various training sample sizes. In these simulations, we generate d-dimensional vectors of prognostic variables, X = (X₁, …, X_d)^T, independently from Uniform[−1, 1]. Treatment A is generated from Uniform[0, 2] independently of X. The response R is normally distributed in N(Q₀(X,A), 1), where Q₀(X,A) reflects the interaction between the treatment and the prognostic variables and is chosen to vary according to the following scenarios:

• Scenario 1:

  $$\begin{array}{c}{Q}_0(\mathbf{X},A)=8+4X_1-2X_2-2X_3-25\times {(f_{\mathit{opt}}(\mathbf{X})-A)}^2,\\ f_{\mathit{opt}}(\mathbf{X})=1+0.5X_1+0.5X_2.\end{array}$$
• Scenario 2:

  $$\begin{array}{c}{Q}_0(\mathbf{X},A)=8+4cos(2\pi X_2)-2X_4-8X_5^3-15\times \mid f_{\mathit{opt}}(\mathbf{X})-A\mid ,\\ f_{\mathit{opt}}(\mathbf{X})=0.6(-0.5<X_1<0.5)+1.2(X_1>0.5)+1.2(X_1<-0.5)+X_4^2+0.5log(\mid X_7\mid +1)-\mathrm{0.6.}\end{array}$$

In Scenario 1, we set d = 30, and the optimal IDR is a linear function of X, and in Scenario 2, d = 10, and the optimal IDR is a nonlinear function of X.

We apply the proposed method to estimate the optimal IDR for each simulated data set. We estimate both a linear IDR (called L-O-learning) and a non-linear IDR using the Gaussian kernel (called K-O-learning). In our O-learning methods, we fix ϕ_n to be 0.1, and the tuning parameters λ_n and γ_n are selected by 5-fold cross validation. For comparison, two competing regression-based methods (the LASSO and SVR) are also considered for estimation. Both methods are two-step procedures similar to Q-learning: in the first step, we estimate the conditional mean of R given (A,X) using either a linear regression model with LASSO penalty (Tibshirani, 1996) or support vector regression (Vapnik, 1995; Smola and Schölkopf, 2004). Then in the second step, for each X, we search for the optimal dose level for A which maximizes the estimated regression mean. Specifically, the covariates used in the LASSO model are (X, A,X²,XA,A²). In other words, we assume that given X, the treatment dose and the reward have a quadratic relationship. Therefore, the second step for finding the optimal dose can be solved analytically. In the SVR method, a Gaussian kernel is used to estimate the non-linear relationship between R and A, as well as the interaction between A and X (Zhao et al., 2009). However, the closed form of the optimal dose in the second step does not exist. We use a grid search procedure to find the optimal treatment dose. In particular, we choose 400 equally spaced grids within the interval (0, 2). The tuning parameters in both LASSO and SVR are selected using 5-fold cross validation. We utilize the R (R Core Team, 2013) package “glmnet” for the LASSO (Friedman et al., 2010) and the “kernlab” package for SVR (Karatzoglou et al., 2004). We evaluate the performance of all methods by comparing the expected values under the estimated rules. The expected values are calculated from the average values of a testing set with 5000 observations. The estimated reward is calculated by plugging the estimated optimal dose into the true underlying value function.

The results from 200 replicates are summarized in Table 1. Each column is the average value function of a method evaluated from the testing set. The standard deviation of the estimated values are given in parentheses. Our methods clearly outperform the competing regression-based methods in most cases, and the difference is more dramatic for small sample size situations. When the sample size is large, L-O-learning and the LASSO work better in Scenario 1, where the true optimal IDR is linear; while K-O-learning and SVR work better in Scenario 2 with a nonlinear true optimal rule. In Figure 2, we also show the mean absolute deviation between the predicted optimal doses and the true optimal doses for all the simulations. The results in the figure show a similar pattern as that in Table 1: the proposed O-learning methods perform best in scenarios with small sample sizes.

Table 1.

Average 𝒱̂(f) from 200 replicates from randomized trials

	n	K-O-learning	L-O-learning	SVR	LASSO
Scenario 1	50	4.78 (0.48)	4.83 (1.40)	−12.21 (7.53)	−15.62 (6.61)
	100	5.69 (0.40)	5.39 (0.93)	−2.57 (6.34)	−9.76 (5.21)
	200	6.68 (0.26)	6.85 (0.34)	3.46 (1.97)	−1.91 (4.65)
	400	7.28 (0.15)	7.41 (0.14)	6.13 (0.47)	7.95 (0.01)
	800	7.54 (0.08)	7.67 (0.08)	7.36 (0.12)	7.97 (0.01)
Scenario 2	50	2.00 (0.29)	1.16 (0.71)	−1.96 (1.70)	−5.58 (2.79)
	100	2.19 (0.43)	1.57 (0.52)	0.24 (1.42)	−4.12 (2.17)
	200	2.84 (0.37)	2.02 (0.30)	2.01 (0.84)	−3.37 (1.38)
	400	3.69 (0.27)	2.30 (0.18)	3.47 (0.37)	−0.92 (3.12)
	800	4.41 (0.19)	2.49 (0.10)	4.35 (0.19)	1.92 (0.69)

Note: the numbers in boldface are the largest for each row.

Figure 2.

Boxplots of the absolute difference of the predicted optimal doses from the truth.

Furthermore, regression-based methods tend to be more sensitive to covariate dimension. To demonstrate this, we conduct additional simulations for Scenario 1 with covariate dimension d = 50 and training sample size n = 800. The estimated value of SVR is 5.51, which is much smaller than the result of the SVR in Table 1 with d = 30. On the other hand, the average value based on our K-O-learning is 7.45, which is comparable to its value when d = 30 and n = 800.

Finally, we also compare the values from the proposed methods to the ones corresponding to fixed dose levels. Specifically, the respective optimal fixed doses are 1.00 for Scenario 1 and 0.85 for Scenario 2, with the respective values equal to 3.8 and 2.7. From Table 1, when the sample size is greater than 100, our methods already yield a larger value function than the optimal value based on either fixed dose. This result indicates that our proposed randomized trial design with our proposed O-learning method can lead to a better dose rule than the fixed dose rule identified through a traditional dose finding trial.

6.2 Simulation for an observational study

In this section, we study three scenarios where the training data are from observational studies. In particular, we want to quantify the performance change of our methods when the propensity score estimation is biased. The simulation setting is the same as in Scenario 2, except the distribution of A may depend on X. Specifically, let TruncN(μ, a, b, σ) denote the truncated normal distribution with mean μ, lower bound a, upper bound b, and standard deviation σ. The dose assignment for Scenario 3–5 follows:

• Scenario 3:

  $$A~\{\begin{array}{l}\text{TruncN}(-0.5+0.5X_1+0.5X_2,0,2,0.5),\text{when}{X}_3<0;\hfill \\ \text{TruncN}(\mid 0.5+1.5X_2\mid ,0,2,1),\text{when}{X}_3>0.\hfill \end{array}$$
• Scenario 4:

  $$A~\text{TruncN}(f_{\mathit{opt}}(\mathbf{X}),0,2,0.5).$$

For both scenarios, dose levels are skewed as compared to the randomized scenarios. When implementing the proposed methods, we first estimate p(a|X) using a log-normal model where the mean is estimated using the boosting algorithm from Zhu et al. (2015). Then, we estimate the optimal IDR using the O-learning procedure. For comparison, we also evaluate the estimated optimal IDR from the proposed method which ignores the propensity score adjustment, i.e., setting p(a|X) to be constant, and from SVR (a regression-based approach).

From the results in Table 2, we observe that the effect of using propensity score adjustment is small for the proposed O-learning methods. In Scenario 3, the O-learning method ignoring the propensity score adjustment performs slightly worse as compared to the one using the propensity scores, yet it is slightly better in Scenario 4. In both scenarios, our methods still outperform SVR. The current simulation scenarios show that the proposed method appears to not be sensitive to misspecified propensity score models, in contrast to the usual observation when treatment options are discrete or even binary. The apparent robustness of our method for the mis-specification of the propensity score is probably due to the choice of the loss function ℓ_ϕ and the use of the DC algorithm. We have shown in Section 3 that in each subproblem of the DC algorithm, only observations whose observed dose is close to the predicted optimal dose will contribute to the loss function. It is reasonable to assume that observations with large observed rewards are more likely to receive the dose close to the optimal. Hence, the observed reward will largely determine which observations contribute most to the loss function and the propensity score will only impact the scale of such contributions. Furthermore, it appears that the errors in the propensity score are largely diluted when treatment is continuous, i.e. patients with large propensity score receiving nearly optimal treatment is a rare occurrence within a simulation. For these reasons, the performance of our methods does not change much with or without using the propensity score. This is an issue we plan on investigating more in the future, along with deriving an accompanying theoretical explanation. Note that for Scenario 4, patients receive doses near the optimal dose level. In particular, the value function of the observed dose assignment rule is about 2.7. As compared to Scenario 2, this suggests our method may have advantages when the observed dose is close to the optimal dose level; however, this is not observed for the SVR approach.

Table 2.

Average 𝒱̂(f) from 200 replicates for observational studies

	n	K-O-learning	K-O-learning-ps	SVR
Scenario 3	200	2.68 (0.30)	2.74 (0.29)	1.99 (0.83)
	800	4.06 (0.30)	4.19 (0.20)	4.09 (0.28)
Scenario 4	200	3.29 (0.28)	3.23 (0.28)	−0.95 (1.57)
	800	4.91 (0.14)	4.73 (0.17)	3.04 (0.52)

Note: “K-O-learning” is the proposed method for a nonlinear IDR, but treating p(A|X) as constant; “K-O-learning-ps” is the proposed method for a linear IDR using the estimated p(A|X). The numbers in boldface are the largest in each row.

7 Warfarin Dosing

Warfarin is a commonly used medicine for preventing thrombosis and thromboembolism. Proper dosing of Warfarin is vitally important, as overdosing predisposes patients to a high risk of bleeding, while underdosing diminishes the drug’s preemptive protection against thrombosis. The international normalized ratio (INR) is a measure of how rapidly the blood can clot, and the INR is actively monitored to ensure the dose of Warfarin is safe and effective. For normal people, the INR is typically 1, but for patients prescribed Warfarin, the therapeutic INR range is typically between 2 to 3 (The International Warfarin Pharmacogenetics Consortium, 2009). Predicting the optimal dose for Warfarin remains an open problem in the medical community, with many methods having been proposed to refine the optimal dose rule (The International Warfarin Pharmacogenetics Consortium, 2009; Hu et al., 2012). The InternationalWarfarin Pharmacogenetics Consortium (2009) compared three methods for predicting Warfarin dose: models by clinical data, models by pharmacogenetic data, and a single fixed dose rule. The paper concluded that pharmacogenetic data yields a better performance for predicting the optimal dose. In The International Warfarin Pharmacogenetics Consortium (2009), patient samples were used for training the prediction model only if the patient’s INR was therapeutically stable and between the 2 to 3 range upon habitually taking Warfarin. The authors fitted a linear model with the received dose as the response and the pharmacogenetic data result as the predictor. Such an approach is valid when the doses received by the patients in the training data are optimal (optimal dose assumption). Later studies found that the pharmacogenetic model proposed by The International Warfarin Pharmacogenetics Consortium (2009) for optimal Warfarin dose identification is suboptimal for elderly patients. Hence, it is reasonable to assume that the optimal dose assumption may be violated in some settings.

For the following analysis, we use the data set from The International Warfarin Pharmacogenetics Consortium (2009). To estimate the optimal dose, we utilize both pharmacogenetic and clinical variables, including age, height, weight, race, CYP2C9 genotype, and VKORC1 genotype, and the use of two classes of medications: Cytochrome P450 enzyme (including phenytoin, carbamazepine, and rifampin) and Amiodarone (Cordarone)). After removing observations with missing data in these covariates, there remained a total of 1732 patients with 189 patients having INRs not in the 2 to 3 range. Instead of using patients with INRs between 2 to 3 after treatment and making the optimal dose assumption, we include all of these 1732 patients in our analysis. To convert the INR to a direct measure of reward, we code R_i = −|INR_i − 2.5| for the i-th individual, as INR = 2.5 is in the ideal range. Note that the study consists of observational data rather than a randomized trial, hence we need to estimate the propensity score for O-learning. Particularly, we use the method described in Section 5 to estimate the optimal IDR.

We randomly split the data into training and testing sets 100 times, independently. We consider the scenario that the training set contains 800 samples, and the testing set contains the rest. The performances of different methods are evaluated by comparing the predicted doses and observed doses across these 100 splits. We choose the interval 10 to 100 for the grids since the 5th and 95th quantiles are 14.77mg/week and 70mg/week in the observed data, respectively.

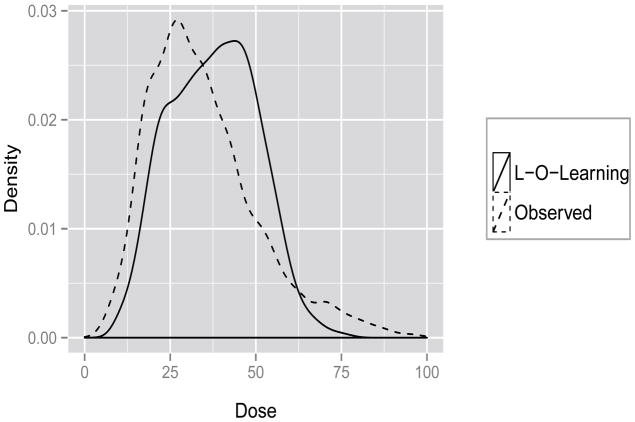
Usually, in practice, the true relationship between dose and reward is unknown, hence we need to estimate the value function for a given dose rule. A potential criterion is 𝒱_ϕ (·), which will involve tuning parameters. We examine whether the methods can yield a reasonable estimated optimal dose as an alternative criterion. The LASSO method predicts all optimal doses to be 10mg/week or 100mg/week due to a vanishing quadratic term for all 100 random splits. Instead, the SVR method predicts that about 70 percent of the patients have optimal doses at extreme values: 20 percent with 10mg/week and 50 percent with 100mg/week. On the other hand, the dose prediction from O-learning is more reasonable, as shown in the density plots from Figure 3 (from one random split for illustration). In the dataset, the majority of the observed doses yield an INR within 2 to 3, hence the observed values should not be far away from optimal. For this reason, we expect the correlation of predicted optimal dose and observed dose to be relatively high if the prediction model performs well. The correlation between predicted dose and observed dose (Corr) for L-O-learning is about 0.60 (sd = 0.08), and the Corr for K-O-learning is 0.32 (sd = 0.06), Corr for SVR is −0.06 (sd = 0.02). In general, L-O-learning performs the best. In addition, L-O-learning suggests decreasing the dose if patients are taking Amiodarone and increasing the dose if patients are taking Cytochrome P450 enzyme (including phenytoin, carbamazepine, and rifampin). This dose suggestion is consistent with what is reported in the literature (Holbrook et al., 2005; The International Warfarin Pharmacogenetics Consortium, 2009). As a remark, our results only reveal some potential predictive biomarkers which the optimal dose levels should depend on. Future trials based on the proposed randomized dose designs are warranted to confirm these findings.

Figure 3.

Distribution of observed and predicted Doses.

8 Discussion

The proposed O-learning method appears to be more effective than alternative approaches in both simulation studies and in the Warfarin example, especially when the training sample size is relatively small. Our method has advantages over regression-based methods through the direct estimation of the optimal dose. As a result, our method is more robust to model specification of the reward. In contrast to O-learning, one needs to correctly specify the model between reward (outcome) and treatment together with the covariates to successfully identify the optimal dose using the indirect methods. Note that the loss function proposed in this paper can be further generalized to |A − f(X)|_ϕ1 − |A − f(X)|_ϕ2 with 0 ≤ ϕ₁ < ϕ₂. In particular, the current loss function is a special case of this general loss with ϕ₁ = 0. Such a generalization provides further robustness to our method at the cost of adding additional tuning parameters in the implementation. Future investigation will also include a comparison between our approaches and other methods based on regrets or contrasts (Murphy, 2003; Robins, 2004).

From the formula in Section 2.1, it is clear that the theoretical solution of f_opt(X) is invariant if we replace the R by R + g(X), where g(X) can be any known function of X. However, analogous to the phenomenon illustrated in Zhou et al. (2015) for personalized binary treatment, the choice of g(X) will impact the performance of O-learning especially when the sample size is small. Choosing a function that can minimize the variance for the dose finding problem would be of great interest. Zhou et al. (2015) recommended a choice of g(X) such that R + g(X) can be interpreted as the residual of a regression model. The authors argued that the residual better reflected the net treatment benefit than the original outcome. In Section 6, we have shown that O-learning and regression-based approaches have different strengths and weaknesses, hence a potential choice of g(X) could come from the regression-based approach.

In practice, the reward could be censored. Techniques such as the inverse probability of censoring weighting could be used to weight the observations; however, such a procedure can yield a less efficient rule. A similar problem can occur when the training data comes from an observational study, as in the Warfarin example. For both situations, it would be valuable to develop doubly robust estimators for IDR. Additional considerations can include accounting for drug toxicity (Thall and Russell, 1998; Laber et al., 2014) and variable selection when estimating the optimal treatment dose.

For some complex diseases, sequential treatments are needed, hence dynamic treatment regimes in place of single stage treatment rules are more useful. For Warfarin dosing, patients need to take the medicine for a set amount of time to become therapeutic, possibly causing the optimal dose to vary over time. Recently, Rich et al. (2014) proposed an adaptive strategy under the framework of structured nested mean models. In addition, other methods for estimating dynamic treatment regimes under a reinforcement learning framework (Sutton and Barto, 1998) have also been proposed in several papers, including Murphy (2003), Zhao et al. (2009) and Moodie et al. (2012), to solve multiple stage optimal treatment problems. Extensions of our proposed method for dynamic treatment regimes would be of great interest.

APPENDIX

A Inconsistency of weighted SVR for IDR estimation

The following Lemma 1 demonstrates that the theoretical minimizer for weighted support vector regression with absolute deviations loss (a special case of ε-insensitive loss used in SVR) is not consistent, i.e. it does not yield a function that maximizes 𝒱(f).

Lemma 1

Let $f_{\mathit{abs}}(\mathbf{X})={\mathit{argmin}}_{f}E\left[\frac{R\mid A-f(\mathbf{X})\mid }{p(A\mid \mathbf{X})}\right]$, then f_abs(X) ≠ f_opt(X).

Proof

By definition, $E[\frac{R\mid A-f(\mathbf{X})\mid }{p(A\mid \mathbf{X})}]=\int E(R\mid a,\mathbf{x})\mid a-f(\mathbf{x})\mid p(\mathbf{x})\mathit{dadx}$. Let p̃(a|x) ∝ E(R|a, x)p(x), then for any given x, f_abs(x) is the median of a with respect to density p̃(a|x). On the other hand, we have proved that f_opt = argmaxE_X[E{R|A = f(X), X}]. This implies that for any given x, f_opt(x) is the mode of a with respect to density p̃(a|x). If p̃(a|x) is not symmetric, then f_abs(x) ≠ f_opt(x). As a result, f_abs(X) ≠ f_opt(X).

Hence, it is not proper to use the absolute deviance loss in O-learning for dose finding. Similarly, we can show that using certain other loss functions, such as quadratic loss, is not consistent either. This follows by the argument that $f_{\mathit{quad}}(\mathbf{X})=\text{argmin}E\left[\frac{R{(A-f(\mathbf{X}))}^2}{p(A\mid \mathbf{X})}\right]$, and for given x, f_quad(x) is the mean of a with respect to density p̃(a|x).

B Proof of Theorem 2

Let $f_{\varphi }^{\ast }$ be the minimizer of ℛ_ϕ(f) and by definition ${\mathcal{R}}_{\varphi }(f)=E\left(\frac{R}{{\varphi }_{n}p(A\mid X)}\right)-{\mathcal{V}}_{\varphi }(f)$. Then

$$\begin{array}{l}\mathcal{V}(f_{\mathit{opt}})-\mathcal{V}({\widehat{f}}_n)=E(R\mid A=f_{\mathit{opt}})-E(R\mid A={\widehat{f}}_n)\\ \le {\mathcal{V}}_{\varphi }(f_{\mathit{opt}})-{\mathcal{V}}_{\varphi }({\widehat{f}}_n)+2C{\varphi }_n\le {\mathcal{R}}_{\varphi }({\widehat{f}}_n)-{\mathcal{R}}_{\varphi }(f_{\mathit{opt}})+2C{\varphi }_n\\ \le {\mathcal{R}}_{\varphi }({\widehat{f}}_n)-{\mathcal{R}}_{\varphi }(f_{\varphi }^{\ast })+c_6{\varphi }_n.\end{array}$$ (5)

The first inequality is due to Theorem 1, and the second follows by the definition of ℛ_ϕ. C is the same constant used in Theorem 1 and c₆ = 2C. Denoting ${\mathcal{R}}_{\varphi }^{\ast }={\mathcal{R}}_{\varphi }(f_{\varphi }^{\ast })$, we can see that

$${\mathcal{R}}_{\varphi }({\widehat{f}}_n)-{\mathcal{R}}_{\varphi }^{\ast }\le {\lambda }_n\Vert {\widehat{f}}_n{\Vert }_k^2+{\mathcal{R}}_{\varphi }({\widehat{f}}_n)-{\mathcal{R}}_{\varphi }^{\ast }=\frac{1}{{\varphi }_n}\left[{\lambda }_n{\varphi }_n\Vert {\widehat{f}}_n{\Vert }_k^2+{\varphi }_n{\mathcal{R}}_{\varphi }({\widehat{f}}_n)-{\varphi }_n{\mathcal{R}}_{\varphi }^{\ast }\right].$$ (6)

Next, we want to bound $\mathbb{G}={\lambda }_n{\varphi }_n\Vert {\widehat{f}}_n{\Vert }_k^2+{\varphi }_n{\mathcal{R}}_{\varphi }({\widehat{f}}_n)-{\varphi }_n{\mathcal{R}}_{\varphi }^{\ast }$. The reason for scaling by the factor ϕ_n is that the corresponding loss function after scaling becomes $L_{\varphi }(\mathbf{X},A,f(\mathbf{X}))=\frac{R{\ell }_{\varphi }(A-f(\mathbf{X}))}{p(A\mid \mathbf{X})}$. L_ϕ(X, A, f(X)) is a bounded loss function when ϕ_n → 0, and such a property will facilitate the proof. In the following theorem, let f̂_n = f_D,λn, ℛ_L,P = ϕ_nℛ_ϕ, and ${\mathcal{R}}_{L,P}^{\ast }={\varphi }_n{\mathcal{R}}_{\varphi }(f_{\varphi }^{\ast })$. Hence, $f_{\varphi }^{\ast }$ is also the minimizer for ℛ_L,P. In the following steps, we rely on the theorem proved by Steinwart and Christmann (2008), given as follows:

Theorem 7.23 (Oracle inequality for SVMs using benign kernels, Steinwart and Christmann, 2008)

Let L : X × A × ℝ → [0, ∞) be a loss function. Also, let H be a separable RKHS of a measurable kernel over X and P be a distribution on X × A. If the following conditions are satisfied:

• (A1)L satisfies the supremum bound L(.) ≤ B for a B > 0.
• (A2)L is a locally Lipschitz continuous loss that can be clipped at M > 0.
• (A3)The variance bound ${\mathbb{E}}_P{(L\circ \stackrel{\sim }{f}-L\circ f_{L,P}^{\ast })}^2\le V·{({\mathbb{E}}_P(L\circ \stackrel{\sim }{f}-L\circ f_{L,P}^{\ast }))}^v$ is satisfied for constants ν ∈ [0, 1], V ≥ B^2−ν, and all f ∈ H.
• (A4)For fixed n ≥ 1, there exist constants p ∈ (0, 1) and a ≥ B such that the entropy number ${\mathbb{E}}_{D_X~P_X^n}{\mathfrak{e}}_i(id:H\to L_2(D_X))\le a{i}^{-\frac{1}{2p}}$, i ≥ 1.

Fix an f₀ ∈ H and a constant B₀ ≥ B such that L ∘ f₀ ≤ B₀. Then, for all fixed τ > 0 and λ_n > 0, the SVM using H and L satisfies

$${\lambda }_n{\varphi }_n\Vert f_{D,{\lambda }_n}{\Vert }_H^2+{\mathcal{R}}_{L,P}({\stackrel{\sim }{f}}_{D,{\lambda }_n})-{\mathcal{R}}_{L,P}^{\ast }\le 9({\lambda }_n{\varphi }_n\Vert f_0{\Vert }_H^2+{\mathcal{R}}_{L,P}(f_0)-{\mathcal{R}}_{L,P}^{\ast })+K_0{(\frac{a^{2p}}{{({\lambda }_n{\varphi }_n)}^{p}n})}^{\frac{1}{2-p-v+vp}}+3{(\frac{72V\tau }{n})}^{\frac{1}{2-v}}+\frac{15B_0\tau }{n}$$

with probability Pⁿ not less than 1 − 3e^−τ, where K₀ ≥ 1 is a constant only depending on p, M, B, ν, and V.

We will verify conditions (A1)–(A4) for our setting as follows: The loss function in our problem is $L_{\varphi }(\mathbf{X},A,f(\mathbf{X}))=\frac{R{\ell }_{\varphi }(A-f(\mathbf{X}))}{p(A\mid \mathbf{X})}$. For our problem, it is reasonable to assume the rewards are bounded and p(A|X) is bounded such that R/p(A|X) ∈ [0, B], where B is some finite constant. Hence, we have L_ϕ(.) ≤ B for (A1).

Note that f̃ is a clipped version of f (via Winsorization) for some value M, such that t̃ = I(|t| ≤ M)t + I(|t| > M)sign(t)M. The risks of L_ϕ(.) loss satisfy ℛ(f̃) ≤ ℛ(f), if we set M to be some large value, i.e. larger than the range of the dose. Hence, L_ϕ(·) can be clipped. This implies we can investigate the clipped version of the loss instead of the original loss function without loss of generality (Steinwart and Christmann, 2008). Furthermore, L_ϕ(.) is Lipschitz continuous with Lipschitz constant equal to B/ϕ_n, hence it is also locally Lipschitz continuous. As a result, condition (A2) is satisfied.

Furthermore, (A3) is true since ${\mathbb{E}}_P{(L_{\varphi }\circ \stackrel{\sim }{f}-L_{\varphi }\circ f_{\varphi }^{\ast })}^2\le 2{\mathbb{E}}_P[{(L_{\varphi }\circ \stackrel{\sim }{f})}^2+{(L_{\varphi }\circ f_{\varphi }^{\ast })}^2]\le 4B^2$.

The benign kernel we implement in the algorithm is the Gaussian kernel. By Theorem 7.34 of Steinwart and Christmann (2008), we have that (A4) holds with the constant a being set equal to $c_{\epsilon ,p}{\gamma }_n^{-\frac{(1-p)(1-\epsilon )d}{2p}}$.

So far, all the conditions needed for Theorem 7.23 are satisfied, hence by plugging in $a=c_{\epsilon ,p}{\gamma }_n^{-\frac{(1-p)(1+\epsilon )d}{2p}}$, ν = 0, V = 4B², and B₀ = B, we obtain

$$\mathbb{G}\le 9A({\lambda }_n)+K_0{[\frac{1}{{\gamma }_n^{(1-p)(1+\epsilon )d}{\lambda }_n^p{\varphi }_n^{p}n}]}^{\frac{1}{2-p}}+36\sqrt{2}B{(\tau /n)}^{\frac{1}{2}}+15B(\tau /n),$$ (7)

where $A({\lambda }_n)={\lambda }_n{\varphi }_n\Vert f_0{\Vert }_{H_{\gamma n}}^2+{\mathcal{R}}_{L,P}(f_0)-{\mathcal{R}}_{L,P}^{\ast }$.

The next step is to bound the approximation error A(λ_n). Since any f₀ ∈ H_γ is valid for Equation (7), we can study a specific choice of f₀ and the corresponding bound for A(λ_n). To construct this f₀, for r ∈ ℕ and γ > 0, we define the function 𝒦 : ℝ^d → ℝ as $\mathcal{K}(x)={\sum }_{j=1}^r\left(\begin{array}{c}r\\ j\end{array}\right){(-1)}^{1-j}\frac{1}{j^d}{\left(\frac{2}{{\gamma }^2\varphi }\right)}^{d/2}{\mathcal{K}}_{j\gamma /\sqrt{2}}(x)$, where ${\mathcal{K}}_{\gamma }=exp(-{\gamma }^2\Vert x{\Vert }_2^2)$ for all x ∈ R^d. Assuming that $f_{\varphi }^{\ast }\in L_2({ℝ}^d)\cap L_{\infty }({ℝ}^d)$, we can define f₀ by convolving 𝒦 with this optimal decision function (Eberts and Steinwart, 2013), that is

$$f_0:=\mathcal{K}\ast f_{\varphi }^{\ast }={\int }_{{ℝ}^d}\mathcal{K}(X-t)f_{\varphi }^{\ast }(t)dt,x\in {ℝ}^d.$$ (8)

With the help of two theorems in Eberts and Steinwart (2013), we can show that f₀ is contained in H_γ, and that it is a suitable function for bounding A(λ_n).

By the construction of f₀, the approximation error for our problem is written as:

$$A({\lambda }_n)={\lambda }_n{\varphi }_n\Vert f_0{\Vert }_{H_{\gamma n}}^2+{\mathcal{R}}_{L,P}(f_0)-{\mathcal{R}}_{L,P}^{\ast }={\lambda }_n{\varphi }_n\Vert \mathcal{K}\ast f_{\varphi }^{\ast }{\Vert }_{H_{\gamma n}}^2+{\mathcal{R}}_{L,P}(\mathcal{K}\ast f_{\varphi }^{\ast })-{\mathcal{R}}_{L,P}^{\ast }.$$

By Theorem 2.3 of Eberts and Steinwart (2013), we have:

$$A({\lambda }_n)\le {\lambda }_n{\varphi }_n{({\gamma }_n\sqrt{\pi })}^{-d}{(2^r-1)}^2\Vert f_{\varphi }^{\ast }{\Vert }_{L_2({ℝ}^d)}^2+{\mathcal{R}}_{L,P}(\mathcal{K}\ast f_{\varphi }^{\ast })-{\mathcal{R}}_{L,P}^{\ast }.$$

By the Lipschitz continuity property of the loss function L_ϕ,

$$A({\lambda }_n)\le {\lambda }_n{\varphi }_n{({\gamma }_n\sqrt{\pi })}^{-d}{(2^r-1)}^2\Vert f_{\varphi }^{\ast }{\Vert }_{L_2({ℝ}^d)}^2+\frac{B}{{\varphi }_n}{\mid \mathcal{K}\ast f_{\varphi }^{\ast }-f_{\varphi }^{\ast }\mid }_{L_1(P_X)}.$$

By Theorem 2.2 of Eberts and Steinwart (2013),

$$A({\lambda }_n)\le {\lambda }_n{\varphi }_n{({\gamma }_n\sqrt{\pi })}^{-d}{(2^r-1)}^2{\Vert f_{\varphi }^{\ast }\Vert }_{L_2({ℝ}^d)}^2+\frac{B}{{\varphi }_n}{C}_{r,1}\Vert g\Vert L_p(P_X){\omega }_{r,L_1({ℝ}^d)}(f_{\varphi }^{\ast },{\gamma }_n/2).$$ (9)

Recall that we assume $f_{\mathit{opt}}\in B_{1,\infty }^{\alpha }({ℝ}^d)$, a Besov space, and if we further assume $f_{\varphi }^{\ast }\in B_{1,\infty }^{\alpha }({ℝ}^d)$, i.e. $B_{1,\infty }^{\alpha }({ℝ}^d)=\{f\in L_{\infty }(({ℝ}^d)):{\mathit{sup}}_{t>0}(t^{-\alpha }{\omega }_{r,L_1(({ℝ}^d))}(f,t))<\infty \}$, then ${\omega }_{r,L_1({ℝ}^d)}(f_{\varphi }^{\ast },{\gamma }_n/2)<c_0{\gamma }_n^{\alpha }$, where c₀ is a constant. Plugging this into inequality (9), and combining with the assumption $f_{\varphi }^{\ast }\in L_2({ℝ}^d)\cap L_{\infty }({ℝ}^d)$, we obtain

$$A({\lambda }_n)\le c_1{\lambda }_n{\varphi }_n{\gamma }_n^{-d}+c_2{\gamma }_n^{\alpha }{\varphi }_n^{-1}.$$ (10)

Combining Equation (6), Equation (7) and Equation (10), we obtain that:

$${\mathcal{R}}_{\varphi }({\widehat{f}}_n)-{\mathcal{R}}_{\varphi }(f_{\varphi }^{\ast })\le c_1{\left[\frac{1}{{\gamma }_n^{(1-p)(1+\epsilon )d}{\lambda }_n^p{\varphi }_n^{2}n}\right]}^{\frac{1}{2-p}}+c_2\frac{{\tau }^{1/2}}{{\varphi }_n{n}^{1/2}}+c_3\frac{\tau }{{\varphi }_{n}n}+c_4\frac{{\lambda }_n}{{\gamma }_n^d}+c_5\frac{{\gamma }_n^{\alpha }}{{\varphi }_n^2}.$$ (11)

Combining Equation (5) and Equation (11) now yields the desired result.