FIGURE 1.
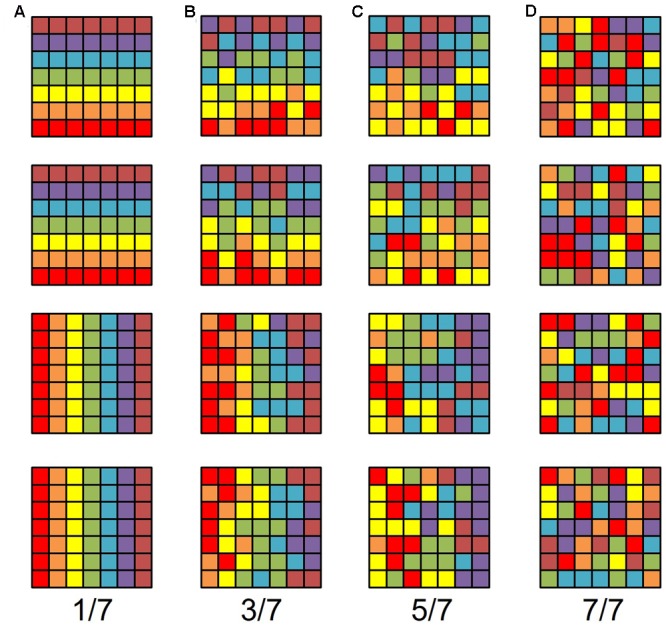
Model gradients. Each row represents one sensory gradient evenly distributed across a piece of cortical surface consisting of a 7 × 7 matrix of voxels. The color code is such that each color represents a stimulus value within 1/7 of the overall stimulus space, ranging from the lowest value in red, in order to the highest value in brown. For example, red would represent an eccentricity preference from fixation value 0.00–1.57° of visual angle with our 11°-radius bar stimulus, green would be 4.71–6.28°, and brown would be 9.43–11.00°. Each column represents gradients with a different amount of random noise in each voxel, such that there is no random noise in the left-most column and completely random noise in the right-most column. In other words, the acceptable noise for each voxel is zero in the leftmost column and looser as one moves rightward. In (A), each voxel represents exactly 1/7th of the stimulus space that it should (e.g., if the voxel should be green, it is, without variation). In (B), if a voxel should represent a particular 1/7th of the stimulus range in the gradient, it can with equal probability represent an adjacent color, such that the true value falls somewhere within 3/7th of the stimulus range, centered on the correct value (e.g., if a voxel should be green, it can be yellow, green, or blue with equal probability). In (C), if a voxel should represent a particular 1/7th of the stimulus range in the gradient, it can with equal probability represent 5/7th of the stimulus range, centered on the correct value (e.g., if a voxel should be green, it can be tan, yellow, green, blue, or purple, with equal probability). In (D), it doesn’t matter what 1/7th of the stimulus space the voxel should represent given the gradient, any color can be assigned to each voxel, with equal probability. Note that gradients in (B) are still identifiable as the same gradients in (A), despite significant noise. Note also that the gradients in (C) have more structure than completely random noise in (D), but are visibly less orderly than the gradients in (B).
