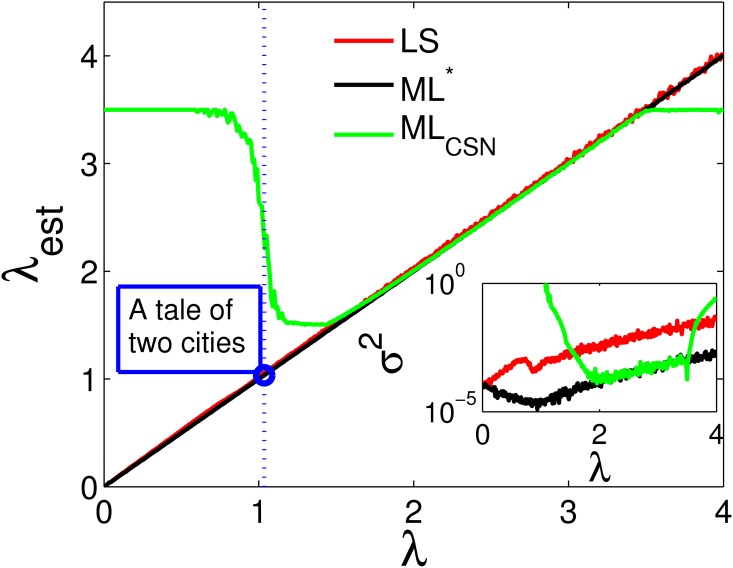
Fig 3. Comparison of the three power-law exponent estimators, LS, ML_CSN, and ML*.

For 400 values of λ in the range between 0 and 4, we sample N = 10,000 events from Ω = {1, ⋯, 1,000}, from a power-law probability distribution p(x|λ, Ω) ∝ x^−λ. The estimated exponents λ_est for the estimators LS (red), the ML_CSN (green, ${\lambda }_{\text{est}}=\widehat{\lambda }$), and the new ML* (black, λ_est = λ*), are plotted against the true value of the exponent λ of the probability distribution samples are drawn from. Clearly, below λ ∼ 1.5 the ML_CSN estimator no longer works reliably. ML_CSN and ML* work equally well in a range of 1.5 < λ < 3.5. Outside this range ML* performs consistently better than the other methods. The inset shows the mean-square error σ² of the estimated exponents. The LS-estimator has a much higher σ² over the entire region, than the ML*-estimator. The blue dot represents the ML* estimate for the Zipf exponent of C. Dickens’ “A tale of two cities”. Clearly, this exponent could never reliably be obtained from the rank ordered distribution using ML_CSN, whereas ML* works fine even for values of λ ∼ 0.