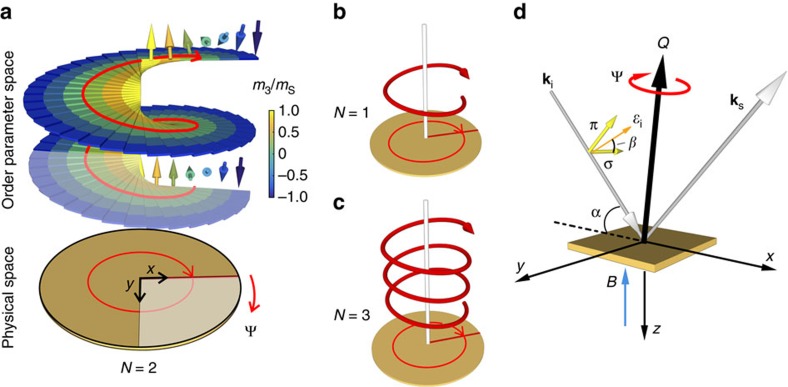
Figure 1. Concept of winding number and experimental setup.

(a) For classical spins in two-dimensional space, the spin configuration that carries a winding number of N, as described by equation (1), can be equivalently constructed by mapping the two-dimensional physical space using one-dimensional helices. In order parameter space, the one-dimensional helices are rotated azimuthally by NΨ from the base position (see, for example, bottom spin helix for Ψ=0°), and projected onto physical space at the azimuthal position Ψ. The helices are stacked up in order parameter space for illustrative purposes following the red helical guideline. The example shows the situation for N=2 where the order parameter space maps the physical space twice. The shaded quarter-circle in physical space (below) corresponds to a covered half-circle in order parameter space (above). Simplified plots for the N=1 and N=3 cases are shown in b,c, respectively. (d) When Ψ covers the range from 0° to 360°, the scattered intensity will exhibit a periodicity that only depends on N. Both circularly or linearly polarized incident light is used, allowing for two measurement strategies: CD plots and PAMs. In both cases, the diffraction condition is met for the wavevector Q, which contains the topological motif's modulation wavevector for different azimuthal angles Ψ. The polarization angle β of the incident light polarization vector 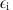is defined with respect to σ-polarization (β=0°; β=90° corresponds to π-polarization).