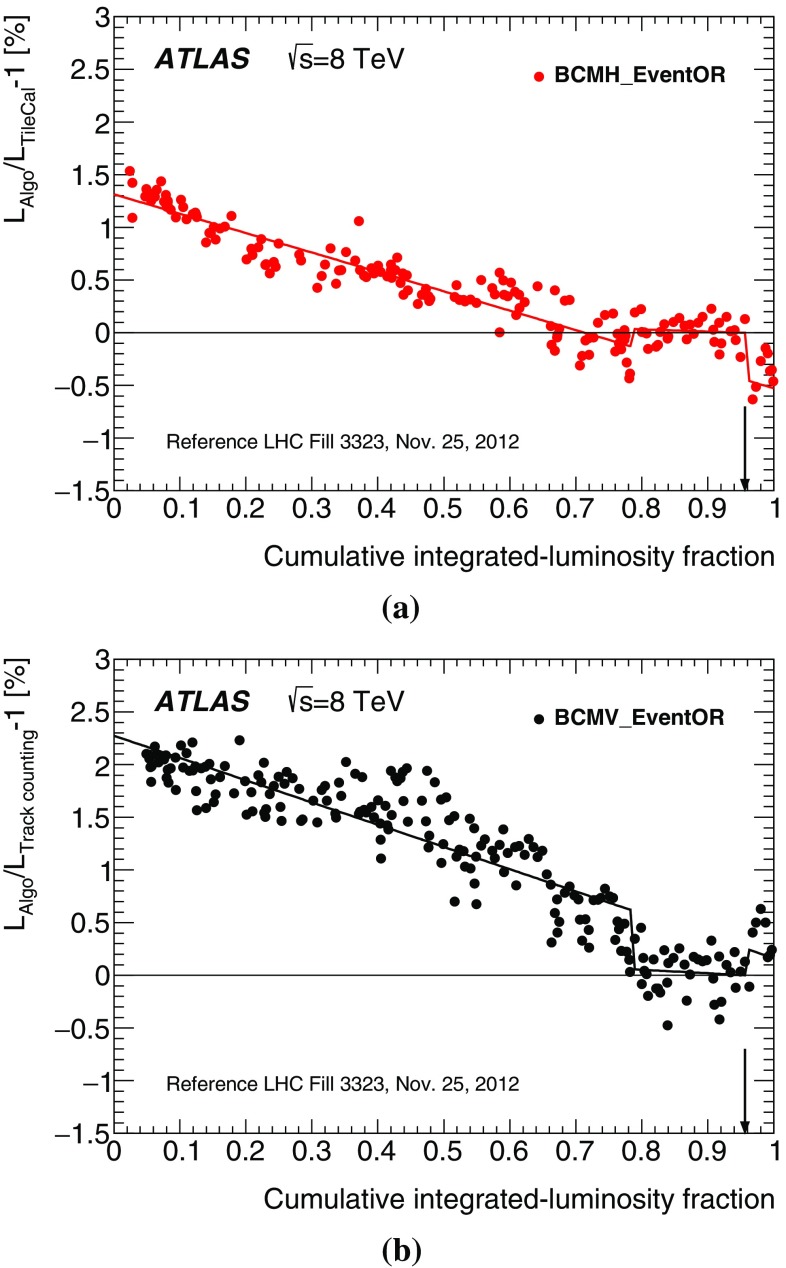
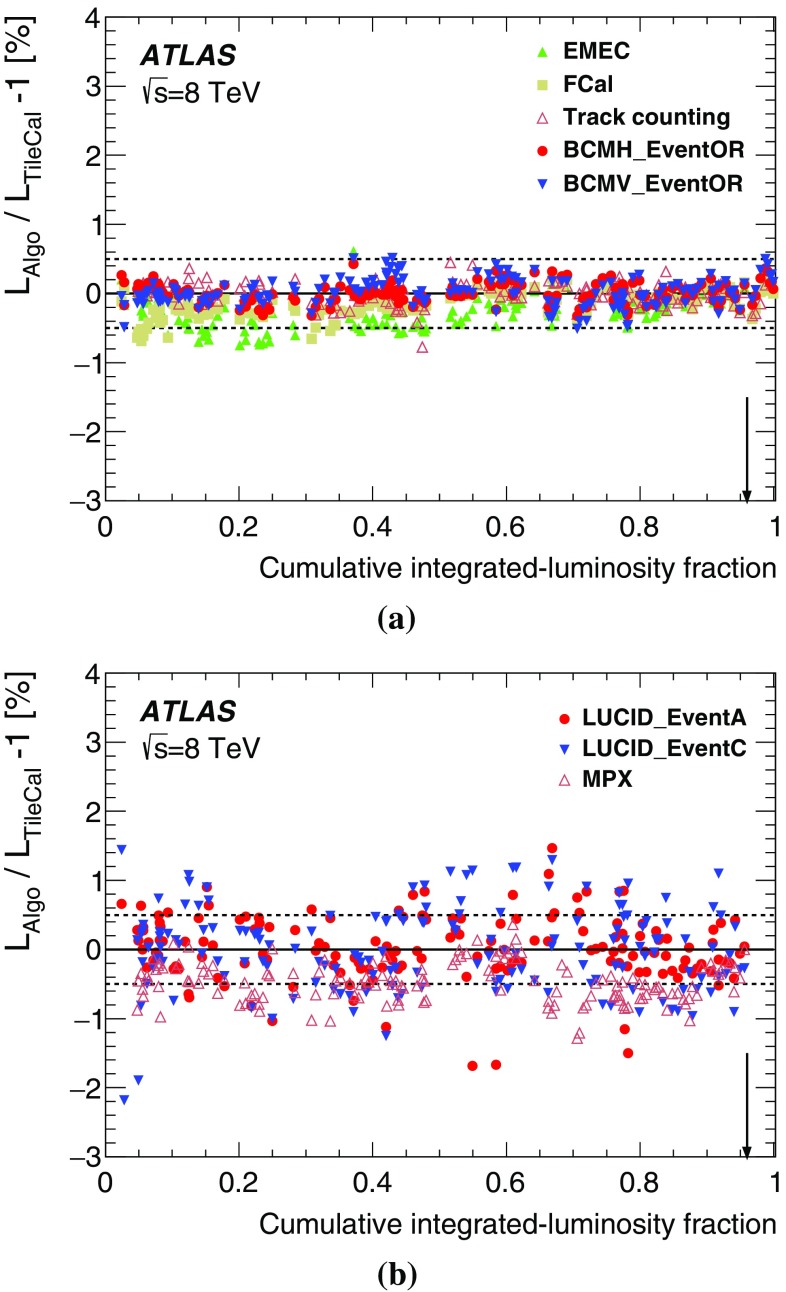
M Aaboud
M Aaboud
180Faculté des Sciences, Université Mohamed Premier and LPTPM, Oujda, Morocco
180,
G Aad
G Aad
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
B Abbott
B Abbott
144Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
144,
J Abdallah
J Abdallah
92University of Iowa, Iowa City, IA USA
92,
O Abdinov
O Abdinov
14Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
14,
B Abeloos
B Abeloos
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
R Aben
R Aben
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
O S AbouZeid
O S AbouZeid
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
N L Abraham
N L Abraham
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
H Abramowicz
H Abramowicz
203Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
203,
H Abreu
H Abreu
202Department of Physics, Technion: Israel Institute of Technology, Haifa, Israel
202,
R Abreu
R Abreu
147Center for High Energy Physics, University of Oregon, Eugene, OR USA
147,
Y Abulaiti
Y Abulaiti
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
B S Acharya
B S Acharya
164Departamento de Fisica Teorica y del Cosmos and CAFPE, Universidad de Granada, Granada, Spain
164,
L Adamczyk
L Adamczyk
60AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Kraków, Poland
60,
D L Adams
D L Adams
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
J Adelman
J Adelman
139Department of Physics, Northern Illinois University, DeKalb, IL USA
139,
S Adomeit
S Adomeit
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
T Adye
T Adye
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
A A Affolder
A A Affolder
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
T Agatonovic-Jovin
T Agatonovic-Jovin
16Institute of Physics, University of Belgrade, Belgrade, Serbia
16,
J Agricola
J Agricola
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
J A Aguilar-Saavedra
J A Aguilar-Saavedra
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
164Departamento de Fisica Teorica y del Cosmos and CAFPE, Universidad de Granada, Granada, Spain
159,164,
S P Ahlen
S P Ahlen
30Department of Physics, Boston University, Boston, MA USA
30,
F Ahmadov
F Ahmadov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
G Aielli
G Aielli
173INFN Sezione di Roma Tor Vergata, Rome, Italy
174Dipartimento di Fisica, Università di Roma Tor Vergata, Rome, Italy
173,174,
H Akerstedt
H Akerstedt
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
T P A Åkesson
T P A Åkesson
111Fysiska institutionen, Lunds universitet, Lund, Sweden
111,
A V Akimov
A V Akimov
126P.N. Lebedev Physical Institute of the Russian, Academy of Sciences, Moscow, Russia
126,
G L Alberghi
G L Alberghi
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
J Albert
J Albert
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
S Albrand
S Albrand
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
M J Alconada Verzini
M J Alconada Verzini
100Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
100,
M Aleksa
M Aleksa
45CERN, Geneva, Switzerland
45,
I N Aleksandrov
I N Aleksandrov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
C Alexa
C Alexa
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
G Alexander
G Alexander
203Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
203,
T Alexopoulos
T Alexopoulos
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
M Alhroob
M Alhroob
144Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
144,
M Aliev
M Aliev
102INFN Sezione di Lecce, Lecce, Italy
103Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
102,103,
G Alimonti
G Alimonti
121INFN Sezione di Milano, Milan, Italy
121,
J Alison
J Alison
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
S P Alkire
S P Alkire
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
B M M Allbrooke
B M M Allbrooke
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
B W Allen
B W Allen
147Center for High Energy Physics, University of Oregon, Eugene, OR USA
147,
P P Allport
P P Allport
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
A Aloisio
A Aloisio
134INFN Sezione di Napoli, Naples, Italy
135Dipartimento di Fisica, Università di Napoli, Naples, Italy
134,135,
A Alonso
A Alonso
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
F Alonso
F Alonso
100Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
100,
C Alpigiani
C Alpigiani
184Department of Physics, University of Washington, Seattle, WA USA
184,
M Alstaty
M Alstaty
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
B Alvarez Gonzalez
B Alvarez Gonzalez
45CERN, Geneva, Switzerland
45,
D Álvarez Piqueras
D Álvarez Piqueras
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
M G Alviggi
M G Alviggi
134INFN Sezione di Napoli, Naples, Italy
135Dipartimento di Fisica, Università di Napoli, Naples, Italy
134,135,
B T Amadio
B T Amadio
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
K Amako
K Amako
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
Y Amaral Coutinho
Y Amaral Coutinho
32Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
32,
C Amelung
C Amelung
31Department of Physics, Brandeis University, Waltham, MA USA
31,
D Amidei
D Amidei
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
S P Amor Dos Santos
S P Amor Dos Santos
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
161Department of Physics, University of Coimbra, Coimbra, Portugal
159,161,
A Amorim
A Amorim
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
160Faculdade de Ciências, Universidade de Lisboa, Lisbon, Portugal
159,160,
S Amoroso
S Amoroso
45CERN, Geneva, Switzerland
45,
G Amundsen
G Amundsen
31Department of Physics, Brandeis University, Waltham, MA USA
31,
C Anastopoulos
C Anastopoulos
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
L S Ancu
L S Ancu
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
N Andari
N Andari
139Department of Physics, Northern Illinois University, DeKalb, IL USA
139,
T Andeen
T Andeen
13Department of Physics, The University of Texas at Austin, Austin, TX USA
13,
C F Anders
C F Anders
84Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
84,
G Anders
G Anders
45CERN, Geneva, Switzerland
45,
J K Anders
J K Anders
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
K J Anderson
K J Anderson
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
A Andreazza
A Andreazza
121INFN Sezione di Milano, Milan, Italy
122Dipartimento di Fisica, Università di Milano, Milan, Italy
121,122,
V Andrei
V Andrei
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
S Angelidakis
S Angelidakis
11Physics Department, University of Athens, Athens, Greece
11,
I Angelozzi
I Angelozzi
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
P Anger
P Anger
67Institut für Kern–und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
67,
A Angerami
A Angerami
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
F Anghinolfi
F Anghinolfi
45CERN, Geneva, Switzerland
45,
A V Anisenkov
A V Anisenkov
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
N Anjos
N Anjos
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
A Annovi
A Annovi
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
M Antonelli
M Antonelli
70INFN Laboratori Nazionali di Frascati, Frascati, Italy
70,
A Antonov
A Antonov
1Department of Physics, University of Adelaide, Adelaide, Australia
128National Research Nuclear University MEPhI, Moscow, Russia
1,128,
F Anulli
F Anulli
171INFN Sezione di Roma, Rome, Italy
171,
M Aoki
M Aoki
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
L Aperio Bella
L Aperio Bella
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
G Arabidze
G Arabidze
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
Y Arai
Y Arai
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
J P Araque
J P Araque
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
159,
A T H Arce
A T H Arce
68Department of Physics, Duke University, Durham, NC USA
68,
F A Arduh
F A Arduh
100Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
100,
J-F Arguin
J-F Arguin
125Group of Particle Physics, University of Montreal, Montreal, QC Canada
125,
S Argyropoulos
S Argyropoulos
92University of Iowa, Iowa City, IA USA
92,
M Arik
M Arik
22Department of Physics, Bogazici University, Istanbul, Turkey
22,
A J Armbruster
A J Armbruster
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
L J Armitage
L J Armitage
106School of Physics and Astronomy, Queen Mary University of London, London, UK
106,
O Arnaez
O Arnaez
45CERN, Geneva, Switzerland
45,
H Arnold
H Arnold
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
M Arratia
M Arratia
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
O Arslan
O Arslan
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
A Artamonov
A Artamonov
127Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
127,
G Artoni
G Artoni
151Department of Physics, Oxford University, Oxford, UK
151,
S Artz
S Artz
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
S Asai
S Asai
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
N Asbah
N Asbah
65DESY, Hamburg and Zeuthen, Germany
65,
A Ashkenazi
A Ashkenazi
203Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
203,
B Åsman
B Åsman
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
L Asquith
L Asquith
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
K Assamagan
K Assamagan
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
R Astalos
R Astalos
190Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
190,
M Atkinson
M Atkinson
218Department of Physics, University of Illinois, Urbana, IL USA
218,
N B Atlay
N B Atlay
187Fachbereich Physik, Universität Siegen, Siegen, Germany
187,
K Augsten
K Augsten
167Czech Technical University in Prague, Prague, Czech Republic
167,
G Avolio
G Avolio
45CERN, Geneva, Switzerland
45,
B Axen
B Axen
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
M K Ayoub
M K Ayoub
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
G Azuelos
G Azuelos
125Group of Particle Physics, University of Montreal, Montreal, QC Canada
125,
M A Baak
M A Baak
45CERN, Geneva, Switzerland
45,
A E Baas
A E Baas
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
M J Baca
M J Baca
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
H Bachacou
H Bachacou
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
K Bachas
K Bachas
102INFN Sezione di Lecce, Lecce, Italy
103Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
102,103,
M Backes
M Backes
45CERN, Geneva, Switzerland
45,
M Backhaus
M Backhaus
45CERN, Geneva, Switzerland
45,
P Bagiacchi
P Bagiacchi
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
P Bagnaia
P Bagnaia
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
Y Bai
Y Bai
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
J T Baines
J T Baines
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
O K Baker
O K Baker
228Department of Physics, Yale University, New Haven, CT USA
228,
E M Baldin
E M Baldin
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
P Balek
P Balek
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
T Balestri
T Balestri
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
F Balli
F Balli
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
W K Balunas
W K Balunas
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
E Banas
E Banas
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
Sw Banerjee
Sw Banerjee
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
A A E Bannoura
A A E Bannoura
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
L Barak
L Barak
45CERN, Geneva, Switzerland
45,
E L Barberio
E L Barberio
118School of Physics, University of Melbourne, Victoria, Australia
118,
D Barberis
D Barberis
73INFN Sezione di Genova, Genoa, Italy
74Dipartimento di Fisica, Università di Genova, Genoa, Italy
73,74,
M Barbero
M Barbero
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
T Barillari
T Barillari
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
T Barklow
T Barklow
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
N Barlow
N Barlow
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
S L Barnes
S L Barnes
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
B M Barnett
B M Barnett
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
R M Barnett
R M Barnett
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
Z Barnovska
Z Barnovska
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
A Baroncelli
A Baroncelli
175INFN Sezione di Roma Tre, Rome, Italy
175,
G Barone
G Barone
31Department of Physics, Brandeis University, Waltham, MA USA
31,
A J Barr
A J Barr
151Department of Physics, Oxford University, Oxford, UK
151,
L Barranco Navarro
L Barranco Navarro
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
F Barreiro
F Barreiro
112Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
112,
J Barreiro Guimarães da Costa
J Barreiro Guimarães da Costa
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
R Bartoldus
R Bartoldus
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
A E Barton
A E Barton
101Physics Department, Lancaster University, Lancaster, UK
101,
P Bartos
P Bartos
190Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
190,
A Basalaev
A Basalaev
155National Research Centre “Kurchatov Institute” B.P. Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
155,
A Bassalat
A Bassalat
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
R L Bates
R L Bates
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
S J Batista
S J Batista
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
J R Batley
J R Batley
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
M Battaglia
M Battaglia
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
M Bauce
M Bauce
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
F Bauer
F Bauer
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
H S Bawa
H S Bawa
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
J B Beacham
J B Beacham
142Ohio State University, Columbus, OH USA
142,
M D Beattie
M D Beattie
101Physics Department, Lancaster University, Lancaster, UK
101,
T Beau
T Beau
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
P H Beauchemin
P H Beauchemin
212Department of Physics and Astronomy, Tufts University, Medford, MA United States of America
212,
P Bechtle
P Bechtle
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
H P Beck
H P Beck
20Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
20,
K Becker
K Becker
151Department of Physics, Oxford University, Oxford, UK
151,
M Becker
M Becker
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
M Beckingham
M Beckingham
222Department of Physics, University of Warwick, Coventry, UK
222,
C Becot
C Becot
141Department of Physics, New York University, New York, NY USA
141,
A J Beddall
A J Beddall
25Faculty of Engineering and Natural Sciences, Bahcesehir University, Istanbul, Turkey
25,
A Beddall
A Beddall
23Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
23,
V A Bednyakov
V A Bednyakov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
M Bedognetti
M Bedognetti
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
C P Bee
C P Bee
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
L J Beemster
L J Beemster
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
T A Beermann
T A Beermann
45CERN, Geneva, Switzerland
45,
M Begel
M Begel
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
J K Behr
J K Behr
65DESY, Hamburg and Zeuthen, Germany
65,
C Belanger-Champagne
C Belanger-Champagne
117Department of Physics, McGill University, Montreal, QC Canada
117,
A S Bell
A S Bell
108Department of Physics and Astronomy, University College London, London, UK
108,
G Bella
G Bella
203Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
203,
L Bellagamba
L Bellagamba
27INFN Sezione di Bologna, Bologna, Italy
27,
A Bellerive
A Bellerive
44Department of Physics, Carleton University, Ottawa, ON Canada
44,
M Bellomo
M Bellomo
116Department of Physics, University of Massachusetts, Amherst, MA USA
116,
K Belotskiy
K Belotskiy
128National Research Nuclear University MEPhI, Moscow, Russia
128,
O Beltramello
O Beltramello
45CERN, Geneva, Switzerland
45,
N L Belyaev
N L Belyaev
128National Research Nuclear University MEPhI, Moscow, Russia
128,
O Benary
O Benary
203Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
203,
D Benchekroun
D Benchekroun
177Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies-Université Hassan II, Casablanca, Morocco
177,
M Bender
M Bender
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
K Bendtz
K Bendtz
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
N Benekos
N Benekos
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
Y Benhammou
Y Benhammou
203Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
203,
E Benhar Noccioli
E Benhar Noccioli
228Department of Physics, Yale University, New Haven, CT USA
228,
J Benitez
J Benitez
92University of Iowa, Iowa City, IA USA
92,
D P Benjamin
D P Benjamin
68Department of Physics, Duke University, Durham, NC USA
68,
J R Bensinger
J R Bensinger
31Department of Physics, Brandeis University, Waltham, MA USA
31,
S Bentvelsen
S Bentvelsen
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
L Beresford
L Beresford
151Department of Physics, Oxford University, Oxford, UK
151,
M Beretta
M Beretta
70INFN Laboratori Nazionali di Frascati, Frascati, Italy
70,
D Berge
D Berge
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
E Bergeaas Kuutmann
E Bergeaas Kuutmann
217Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
217,
N Berger
N Berger
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
J Beringer
J Beringer
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
S Berlendis
S Berlendis
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
N R Bernard
N R Bernard
116Department of Physics, University of Massachusetts, Amherst, MA USA
116,
C Bernius
C Bernius
141Department of Physics, New York University, New York, NY USA
141,
F U Bernlochner
F U Bernlochner
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
T Berry
T Berry
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
P Berta
P Berta
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
C Bertella
C Bertella
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
G Bertoli
G Bertoli
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
F Bertolucci
F Bertolucci
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
I A Bertram
I A Bertram
101Physics Department, Lancaster University, Lancaster, UK
101,
C Bertsche
C Bertsche
65DESY, Hamburg and Zeuthen, Germany
65,
D Bertsche
D Bertsche
144Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
144,
G J Besjes
G J Besjes
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
O Bessidskaia Bylund
O Bessidskaia Bylund
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
M Bessner
M Bessner
65DESY, Hamburg and Zeuthen, Germany
65,
N Besson
N Besson
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
C Betancourt
C Betancourt
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
S Bethke
S Bethke
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
A J Bevan
A J Bevan
106School of Physics and Astronomy, Queen Mary University of London, London, UK
106,
W Bhimji
W Bhimji
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
R M Bianchi
R M Bianchi
158Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
158,
L Bianchini
L Bianchini
31Department of Physics, Brandeis University, Waltham, MA USA
31,
M Bianco
M Bianco
45CERN, Geneva, Switzerland
45,
O Biebel
O Biebel
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
D Biedermann
D Biedermann
19Department of Physics, Humboldt University, Berlin, Germany
19,
R Bielski
R Bielski
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
N V Biesuz
N V Biesuz
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
M Biglietti
M Biglietti
175INFN Sezione di Roma Tre, Rome, Italy
175,
J Bilbao De Mendizabal
J Bilbao De Mendizabal
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
H Bilokon
H Bilokon
70INFN Laboratori Nazionali di Frascati, Frascati, Italy
70,
M Bindi
M Bindi
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
S Binet
S Binet
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
A Bingul
A Bingul
23Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
23,
C Bini
C Bini
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
S Biondi
S Biondi
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
D M Bjergaard
D M Bjergaard
68Department of Physics, Duke University, Durham, NC USA
68,
C W Black
C W Black
200School of Physics, University of Sydney, Sydney, Australia
200,
J E Black
J E Black
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
K M Black
K M Black
30Department of Physics, Boston University, Boston, MA USA
30,
D Blackburn
D Blackburn
184Department of Physics, University of Washington, Seattle, WA USA
184,
R E Blair
R E Blair
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
J-B Blanchard
J-B Blanchard
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
J E Blanco
J E Blanco
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
T Blazek
T Blazek
190Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
190,
I Bloch
I Bloch
65DESY, Hamburg and Zeuthen, Germany
65,
C Blocker
C Blocker
31Department of Physics, Brandeis University, Waltham, MA USA
31,
W Blum
W Blum
1Department of Physics, University of Adelaide, Adelaide, Australia
113Institut für Physik, Universität Mainz, Mainz, Germany
1,113,
U Blumenschein
U Blumenschein
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
S Blunier
S Blunier
47Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
47,
G J Bobbink
G J Bobbink
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
V S Bobrovnikov
V S Bobrovnikov
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
S S Bocchetta
S S Bocchetta
111Fysiska institutionen, Lunds universitet, Lund, Sweden
111,
A Bocci
A Bocci
68Department of Physics, Duke University, Durham, NC USA
68,
C Bock
C Bock
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
M Boehler
M Boehler
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
D Boerner
D Boerner
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
J A Bogaerts
J A Bogaerts
45CERN, Geneva, Switzerland
45,
D Bogavac
D Bogavac
16Institute of Physics, University of Belgrade, Belgrade, Serbia
16,
A G Bogdanchikov
A G Bogdanchikov
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
C Bohm
C Bohm
195Department of Physics, Stockholm University, Stockholm, Sweden
195,
V Boisvert
V Boisvert
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
P Bokan
P Bokan
16Institute of Physics, University of Belgrade, Belgrade, Serbia
16,
T Bold
T Bold
60AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Kraków, Poland
60,
A S Boldyrev
A S Boldyrev
214INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
216Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
214,216,
M Bomben
M Bomben
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
M Bona
M Bona
106School of Physics and Astronomy, Queen Mary University of London, London, UK
106,
M Boonekamp
M Boonekamp
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
A Borisov
A Borisov
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
G Borissov
G Borissov
101Physics Department, Lancaster University, Lancaster, UK
101,
J Bortfeldt
J Bortfeldt
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
D Bortoletto
D Bortoletto
151Department of Physics, Oxford University, Oxford, UK
151,
V Bortolotto
V Bortolotto
87Department of Physics, The Chinese University of Hong Kong, Shatin, NT Hong Kong
88Department of Physics, The University of Hong Kong, Pokfulam, Hong Kong
89Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
87,88,89,
K Bos
K Bos
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
D Boscherini
D Boscherini
27INFN Sezione di Bologna, Bologna, Italy
27,
M Bosman
M Bosman
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
J D Bossio Sola
J D Bossio Sola
42Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
42,
J Boudreau
J Boudreau
158Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
158,
J Bouffard
J Bouffard
2Physics Department, SUNY Albany, Albany, NY USA
2,
E V Bouhova-Thacker
E V Bouhova-Thacker
101Physics Department, Lancaster University, Lancaster, UK
101,
D Boumediene
D Boumediene
55Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
55,
C Bourdarios
C Bourdarios
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
S K Boutle
S K Boutle
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
A Boveia
A Boveia
45CERN, Geneva, Switzerland
45,
J Boyd
J Boyd
45CERN, Geneva, Switzerland
45,
I R Boyko
I R Boyko
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
J Bracinik
J Bracinik
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
A Brandt
A Brandt
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
G Brandt
G Brandt
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
O Brandt
O Brandt
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
U Bratzler
U Bratzler
206Graduate School of Science and Technology, Tokyo Metropolitan University, Tokyo, Japan
206,
B Brau
B Brau
116Department of Physics, University of Massachusetts, Amherst, MA USA
116,
J E Brau
J E Brau
147Center for High Energy Physics, University of Oregon, Eugene, OR USA
147,
H M Braun
H M Braun
1Department of Physics, University of Adelaide, Adelaide, Australia
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
1,227,
W D Breaden Madden
W D Breaden Madden
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
K Brendlinger
K Brendlinger
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
A J Brennan
A J Brennan
118School of Physics, University of Melbourne, Victoria, Australia
118,
L Brenner
L Brenner
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
R Brenner
R Brenner
217Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
217,
S Bressler
S Bressler
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
T M Bristow
T M Bristow
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
D Britton
D Britton
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
D Britzger
D Britzger
65DESY, Hamburg and Zeuthen, Germany
65,
F M Brochu
F M Brochu
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
I Brock
I Brock
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
R Brock
R Brock
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
G Brooijmans
G Brooijmans
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
T Brooks
T Brooks
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
W K Brooks
W K Brooks
48Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
48,
J Brosamer
J Brosamer
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
E Brost
E Brost
147Center for High Energy Physics, University of Oregon, Eugene, OR USA
147,
J H Broughton
J H Broughton
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
P A Bruckman de Renstrom
P A Bruckman de Renstrom
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
D Bruncko
D Bruncko
191Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
191,
R Bruneliere
R Bruneliere
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
A Bruni
A Bruni
27INFN Sezione di Bologna, Bologna, Italy
27,
G Bruni
G Bruni
27INFN Sezione di Bologna, Bologna, Italy
27,
L S Bruni
L S Bruni
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
BH Brunt
BH Brunt
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
M Bruschi
M Bruschi
27INFN Sezione di Bologna, Bologna, Italy
27,
N Bruscino
N Bruscino
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
P Bryant
P Bryant
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
L Bryngemark
L Bryngemark
111Fysiska institutionen, Lunds universitet, Lund, Sweden
111,
T Buanes
T Buanes
17Department for Physics and Technology, University of Bergen, Bergen, Norway
17,
Q Buat
Q Buat
188Department of Physics, Simon Fraser University, Burnaby, BC Canada
188,
P Buchholz
P Buchholz
187Fachbereich Physik, Universität Siegen, Siegen, Germany
187,
A G Buckley
A G Buckley
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
I A Budagov
I A Budagov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
F Buehrer
F Buehrer
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
M K Bugge
M K Bugge
150Department of Physics, University of Oslo, Oslo, Norway
150,
O Bulekov
O Bulekov
128National Research Nuclear University MEPhI, Moscow, Russia
128,
D Bullock
D Bullock
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
H Burckhart
H Burckhart
45CERN, Geneva, Switzerland
45,
S Burdin
S Burdin
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
C D Burgard
C D Burgard
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
B Burghgrave
B Burghgrave
139Department of Physics, Northern Illinois University, DeKalb, IL USA
139,
K Burka
K Burka
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
S Burke
S Burke
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
I Burmeister
I Burmeister
66Lehrstuhl für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
66,
E Busato
E Busato
55Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
55,
D Büscher
D Büscher
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
V Büscher
V Büscher
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
P Bussey
P Bussey
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
J M Butler
J M Butler
30Department of Physics, Boston University, Boston, MA USA
30,
C M Buttar
C M Buttar
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
J M Butterworth
J M Butterworth
108Department of Physics and Astronomy, University College London, London, UK
108,
P Butti
P Butti
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
W Buttinger
W Buttinger
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
A Buzatu
A Buzatu
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
A R Buzykaev
A R Buzykaev
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
S Cabrera Urbán
S Cabrera Urbán
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
D Caforio
D Caforio
167Czech Technical University in Prague, Prague, Czech Republic
167,
V M Cairo
V M Cairo
58INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Cosenza, Italy
59Dipartimento di Fisica, Università della Calabria, Rende, Italy
58,59,
O Cakir
O Cakir
4Department of Physics, Ankara University, Ankara, Turkey
4,
N Calace
N Calace
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
P Calafiura
P Calafiura
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
A Calandri
A Calandri
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
G Calderini
G Calderini
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
P Calfayan
P Calfayan
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
L P Caloba
L P Caloba
32Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
32,
D Calvet
D Calvet
55Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
55,
S Calvet
S Calvet
55Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
55,
T P Calvet
T P Calvet
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
R Camacho Toro
R Camacho Toro
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
S Camarda
S Camarda
45CERN, Geneva, Switzerland
45,
P Camarri
P Camarri
173INFN Sezione di Roma Tor Vergata, Rome, Italy
174Dipartimento di Fisica, Università di Roma Tor Vergata, Rome, Italy
173,174,
D Cameron
D Cameron
150Department of Physics, University of Oslo, Oslo, Norway
150,
R Caminal Armadans
R Caminal Armadans
218Department of Physics, University of Illinois, Urbana, IL USA
218,
C Camincher
C Camincher
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
S Campana
S Campana
45CERN, Geneva, Switzerland
45,
M Campanelli
M Campanelli
108Department of Physics and Astronomy, University College London, London, UK
108,
A Camplani
A Camplani
121INFN Sezione di Milano, Milan, Italy
122Dipartimento di Fisica, Università di Milano, Milan, Italy
121,122,
A Campoverde
A Campoverde
187Fachbereich Physik, Universität Siegen, Siegen, Germany
187,
V Canale
V Canale
134INFN Sezione di Napoli, Naples, Italy
135Dipartimento di Fisica, Università di Napoli, Naples, Italy
134,135,
A Canepa
A Canepa
209TRIUMF, Vancouver, BC Canada
209,
M Cano Bret
M Cano Bret
53Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University (also affiliated with PKU-CHEP), Shanghai, China
53,
J Cantero
J Cantero
145Department of Physics, Oklahoma State University, Stillwater, OK USA
145,
R Cantrill
R Cantrill
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
159,
T Cao
T Cao
63Physics Department, Southern Methodist University, Dallas, TX USA
63,
M D M Capeans Garrido
M D M Capeans Garrido
45CERN, Geneva, Switzerland
45,
I Caprini
I Caprini
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
M Caprini
M Caprini
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
M Capua
M Capua
58INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Cosenza, Italy
59Dipartimento di Fisica, Università della Calabria, Rende, Italy
58,59,
R Caputo
R Caputo
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
R M Carbone
R M Carbone
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
R Cardarelli
R Cardarelli
173INFN Sezione di Roma Tor Vergata, Rome, Italy
173,
F Cardillo
F Cardillo
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
I Carli
I Carli
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
T Carli
T Carli
45CERN, Geneva, Switzerland
45,
G Carlino
G Carlino
134INFN Sezione di Napoli, Naples, Italy
134,
L Carminati
L Carminati
121INFN Sezione di Milano, Milan, Italy
122Dipartimento di Fisica, Università di Milano, Milan, Italy
121,122,
S Caron
S Caron
137Institute for Mathematics Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
137,
E Carquin
E Carquin
48Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
48,
G D Carrillo-Montoya
G D Carrillo-Montoya
45CERN, Geneva, Switzerland
45,
J R Carter
J R Carter
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
J Carvalho
J Carvalho
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
161Department of Physics, University of Coimbra, Coimbra, Portugal
159,161,
D Casadei
D Casadei
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
M P Casado
M P Casado
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
M Casolino
M Casolino
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
D W Casper
D W Casper
213Department of Physics and Astronomy, University of California Irvine, Irvine, CA USA
213,
E Castaneda-Miranda
E Castaneda-Miranda
192Department of Physics, University of Cape Town, Cape Town, South Africa
192,
R Castelijn
R Castelijn
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
A Castelli
A Castelli
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
V Castillo Gimenez
V Castillo Gimenez
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
N F Castro
N F Castro
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
159,
A Catinaccio
A Catinaccio
45CERN, Geneva, Switzerland
45,
J R Catmore
J R Catmore
150Department of Physics, University of Oslo, Oslo, Norway
150,
A Cattai
A Cattai
45CERN, Geneva, Switzerland
45,
J Caudron
J Caudron
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
V Cavaliere
V Cavaliere
218Department of Physics, University of Illinois, Urbana, IL USA
218,
E Cavallaro
E Cavallaro
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
D Cavalli
D Cavalli
121INFN Sezione di Milano, Milan, Italy
121,
M Cavalli-Sforza
M Cavalli-Sforza
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
V Cavasinni
V Cavasinni
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
F Ceradini
F Ceradini
175INFN Sezione di Roma Tre, Rome, Italy
176Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
175,176,
L Cerda Alberich
L Cerda Alberich
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
B C Cerio
B C Cerio
68Department of Physics, Duke University, Durham, NC USA
68,
A S Cerqueira
A S Cerqueira
33Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
33,
A Cerri
A Cerri
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
L Cerrito
L Cerrito
106School of Physics and Astronomy, Queen Mary University of London, London, UK
106,
F Cerutti
F Cerutti
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
M Cerv
M Cerv
45CERN, Geneva, Switzerland
45,
A Cervelli
A Cervelli
20Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
20,
S A Cetin
S A Cetin
24Faculty of Engineering and Natural Sciences, Istanbul Bilgi University, Istanbul, Turkey
24,
A Chafaq
A Chafaq
177Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies-Université Hassan II, Casablanca, Morocco
177,
D Chakraborty
D Chakraborty
139Department of Physics, Northern Illinois University, DeKalb, IL USA
139,
S K Chan
S K Chan
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
Y L Chan
Y L Chan
87Department of Physics, The Chinese University of Hong Kong, Shatin, NT Hong Kong
87,
P Chang
P Chang
218Department of Physics, University of Illinois, Urbana, IL USA
218,
J D Chapman
J D Chapman
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
D G Charlton
D G Charlton
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
A Chatterjee
A Chatterjee
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
C C Chau
C C Chau
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
C A Chavez Barajas
C A Chavez Barajas
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
S Che
S Che
142Ohio State University, Columbus, OH USA
142,
S Cheatham
S Cheatham
101Physics Department, Lancaster University, Lancaster, UK
101,
A Chegwidden
A Chegwidden
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
S Chekanov
S Chekanov
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
S V Chekulaev
S V Chekulaev
209TRIUMF, Vancouver, BC Canada
209,
G A Chelkov
G A Chelkov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
M A Chelstowska
M A Chelstowska
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
C Chen
C Chen
93Department of Physics and Astronomy, Iowa State University, Ames, IA USA
93,
H Chen
H Chen
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
K Chen
K Chen
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
S Chen
S Chen
51Department of Physics, Nanjing University, Jiangsu, China
51,
S Chen
S Chen
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
X Chen
X Chen
54Physics Department, Tsinghua University, Beijing, 100084 China
54,
Y Chen
Y Chen
96Graduate School of Science, Kobe University, Kobe, Japan
96,
H C Cheng
H C Cheng
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
H J Cheng
H J Cheng
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
Y Cheng
Y Cheng
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
A Cheplakov
A Cheplakov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
E Cheremushkina
E Cheremushkina
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
R Cherkaoui El Moursli
R Cherkaoui El Moursli
181Faculté des , Sciences, Université Mohammed V, Rabat, Morocco
181,
V Chernyatin
V Chernyatin
1Department of Physics, University of Adelaide, Adelaide, Australia
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
1,36,
E Cheu
E Cheu
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
L Chevalier
L Chevalier
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
V Chiarella
V Chiarella
70INFN Laboratori Nazionali di Frascati, Frascati, Italy
70,
G Chiarelli
G Chiarelli
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
G Chiodini
G Chiodini
102INFN Sezione di Lecce, Lecce, Italy
102,
A S Chisholm
A S Chisholm
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
A Chitan
A Chitan
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
M V Chizhov
M V Chizhov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
K Choi
K Choi
90Department of Physics, Indiana University, Bloomington, IN USA
90,
A R Chomont
A R Chomont
55Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
55,
S Chouridou
S Chouridou
11Physics Department, University of Athens, Athens, Greece
11,
B K B Chow
B K B Chow
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
V Christodoulou
V Christodoulou
108Department of Physics and Astronomy, University College London, London, UK
108,
D Chromek-Burckhart
D Chromek-Burckhart
45CERN, Geneva, Switzerland
45,
J Chudoba
J Chudoba
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
A J Chuinard
A J Chuinard
117Department of Physics, McGill University, Montreal, QC Canada
117,
J J Chwastowski
J J Chwastowski
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
L Chytka
L Chytka
146Palacký University, RCPTM, Olomouc, Czech Republic
146,
G Ciapetti
G Ciapetti
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
A K Ciftci
A K Ciftci
4Department of Physics, Ankara University, Ankara, Turkey
4,
D Cinca
D Cinca
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
V Cindro
V Cindro
105Department of Physics, Jožef Stefan Institute, University of Ljubljana, Ljubljana, Slovenia
105,
I A Cioara
I A Cioara
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
A Ciocio
A Ciocio
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
F Cirotto
F Cirotto
134INFN Sezione di Napoli, Naples, Italy
135Dipartimento di Fisica, Università di Napoli, Naples, Italy
134,135,
Z H Citron
Z H Citron
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
M Citterio
M Citterio
121INFN Sezione di Milano, Milan, Italy
121,
M Ciubancan
M Ciubancan
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
A Clark
A Clark
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
B L Clark
B L Clark
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
M R Clark
M R Clark
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
P J Clark
P J Clark
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
R N Clarke
R N Clarke
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
C Clement
C Clement
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
Y Coadou
Y Coadou
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
M Cobal
M Cobal
214INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
216Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
214,216,
A Coccaro
A Coccaro
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
J Cochran
J Cochran
93Department of Physics and Astronomy, Iowa State University, Ames, IA USA
93,
L Coffey
L Coffey
31Department of Physics, Brandeis University, Waltham, MA USA
31,
L Colasurdo
L Colasurdo
137Institute for Mathematics Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
137,
B Cole
B Cole
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
A P Colijn
A P Colijn
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
J Collot
J Collot
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
T Colombo
T Colombo
45CERN, Geneva, Switzerland
45,
G Compostella
G Compostella
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
P Conde Muiño
P Conde Muiño
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
160Faculdade de Ciências, Universidade de Lisboa, Lisbon, Portugal
159,160,
E Coniavitis
E Coniavitis
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
S H Connell
S H Connell
193Department of Physics, University of Johannesburg, Johannesburg, South Africa
193,
I A Connelly
I A Connelly
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
V Consorti
V Consorti
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
S Constantinescu
S Constantinescu
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
G Conti
G Conti
45CERN, Geneva, Switzerland
45,
F Conventi
F Conventi
134INFN Sezione di Napoli, Naples, Italy
134,
M Cooke
M Cooke
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
B D Cooper
B D Cooper
108Department of Physics and Astronomy, University College London, London, UK
108,
A M Cooper-Sarkar
A M Cooper-Sarkar
151Department of Physics, Oxford University, Oxford, UK
151,
K J R Cormier
K J R Cormier
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
T Cornelissen
T Cornelissen
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
M Corradi
M Corradi
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
F Corriveau
F Corriveau
117Department of Physics, McGill University, Montreal, QC Canada
117,
A Corso-Radu
A Corso-Radu
213Department of Physics and Astronomy, University of California Irvine, Irvine, CA USA
213,
A Cortes-Gonzalez
A Cortes-Gonzalez
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
G Cortiana
G Cortiana
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
G Costa
G Costa
121INFN Sezione di Milano, Milan, Italy
121,
M J Costa
M J Costa
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
D Costanzo
D Costanzo
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
G Cottin
G Cottin
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
G Cowan
G Cowan
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
B E Cox
B E Cox
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
K Cranmer
K Cranmer
141Department of Physics, New York University, New York, NY USA
141,
S J Crawley
S J Crawley
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
G Cree
G Cree
44Department of Physics, Carleton University, Ottawa, ON Canada
44,
S Crépé-Renaudin
S Crépé-Renaudin
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
F Crescioli
F Crescioli
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
W A Cribbs
W A Cribbs
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
M Crispin Ortuzar
M Crispin Ortuzar
151Department of Physics, Oxford University, Oxford, UK
151,
M Cristinziani
M Cristinziani
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
V Croft
V Croft
137Institute for Mathematics Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
137,
G Crosetti
G Crosetti
58INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Cosenza, Italy
59Dipartimento di Fisica, Università della Calabria, Rende, Italy
58,59,
T Cuhadar Donszelmann
T Cuhadar Donszelmann
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
J Cummings
J Cummings
228Department of Physics, Yale University, New Haven, CT USA
228,
M Curatolo
M Curatolo
70INFN Laboratori Nazionali di Frascati, Frascati, Italy
70,
J Cúth
J Cúth
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
C Cuthbert
C Cuthbert
200School of Physics, University of Sydney, Sydney, Australia
200,
H Czirr
H Czirr
187Fachbereich Physik, Universität Siegen, Siegen, Germany
187,
P Czodrowski
P Czodrowski
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
G D’amen
G D’amen
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
S D’Auria
S D’Auria
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
M D’Onofrio
M D’Onofrio
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
M J Da Cunha Sargedas De Sousa
M J Da Cunha Sargedas De Sousa
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
160Faculdade de Ciências, Universidade de Lisboa, Lisbon, Portugal
159,160,
C Da Via
C Da Via
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
W Dabrowski
W Dabrowski
60AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Kraków, Poland
60,
T Dado
T Dado
190Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
190,
T Dai
T Dai
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
O Dale
O Dale
17Department for Physics and Technology, University of Bergen, Bergen, Norway
17,
F Dallaire
F Dallaire
125Group of Particle Physics, University of Montreal, Montreal, QC Canada
125,
C Dallapiccola
C Dallapiccola
116Department of Physics, University of Massachusetts, Amherst, MA USA
116,
M Dam
M Dam
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
J R Dandoy
J R Dandoy
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
N P Dang
N P Dang
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
A C Daniells
A C Daniells
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
N S Dann
N S Dann
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
M Danninger
M Danninger
220Department of Physics, University of British Columbia, Vancouver, BC Canada
220,
M Dano Hoffmann
M Dano Hoffmann
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
V Dao
V Dao
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
G Darbo
G Darbo
73INFN Sezione di Genova, Genoa, Italy
73,
S Darmora
S Darmora
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
J Dassoulas
J Dassoulas
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
A Dattagupta
A Dattagupta
90Department of Physics, Indiana University, Bloomington, IN USA
90,
W Davey
W Davey
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
C David
C David
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
T Davidek
T Davidek
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
M Davies
M Davies
203Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
203,
P Davison
P Davison
108Department of Physics and Astronomy, University College London, London, UK
108,
E Dawe
E Dawe
118School of Physics, University of Melbourne, Victoria, Australia
118,
I Dawson
I Dawson
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
R K Daya-Ishmukhametova
R K Daya-Ishmukhametova
116Department of Physics, University of Massachusetts, Amherst, MA USA
116,
K De
K De
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
R de Asmundis
R de Asmundis
134INFN Sezione di Napoli, Naples, Italy
134,
A De Benedetti
A De Benedetti
144Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
144,
S De Castro
S De Castro
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
S De Cecco
S De Cecco
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
N De Groot
N De Groot
137Institute for Mathematics Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
137,
P de Jong
P de Jong
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
H De la Torre
H De la Torre
112Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
112,
F De Lorenzi
F De Lorenzi
93Department of Physics and Astronomy, Iowa State University, Ames, IA USA
93,
A De Maria
A De Maria
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
D De Pedis
D De Pedis
171INFN Sezione di Roma, Rome, Italy
171,
A De Salvo
A De Salvo
171INFN Sezione di Roma, Rome, Italy
171,
U De Sanctis
U De Sanctis
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
A De Santo
A De Santo
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
J B De Vivie De Regie
J B De Vivie De Regie
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
W J Dearnaley
W J Dearnaley
101Physics Department, Lancaster University, Lancaster, UK
101,
R Debbe
R Debbe
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
C Debenedetti
C Debenedetti
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
D V Dedovich
D V Dedovich
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
N Dehghanian
N Dehghanian
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
I Deigaard
I Deigaard
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
M Del Gaudio
M Del Gaudio
58INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Cosenza, Italy
59Dipartimento di Fisica, Università della Calabria, Rende, Italy
58,59,
J Del Peso
J Del Peso
112Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
112,
T Del Prete
T Del Prete
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
D Delgove
D Delgove
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
F Deliot
F Deliot
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
C M Delitzsch
C M Delitzsch
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
M Deliyergiyev
M Deliyergiyev
105Department of Physics, Jožef Stefan Institute, University of Ljubljana, Ljubljana, Slovenia
105,
A Dell’Acqua
A Dell’Acqua
45CERN, Geneva, Switzerland
45,
L Dell’Asta
L Dell’Asta
30Department of Physics, Boston University, Boston, MA USA
30,
M Dell’Orso
M Dell’Orso
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
M Della Pietra
M Della Pietra
134INFN Sezione di Napoli, Naples, Italy
134,
D della Volpe
D della Volpe
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
M Delmastro
M Delmastro
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
P A Delsart
P A Delsart
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
C Deluca
C Deluca
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
D A DeMarco
D A DeMarco
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
S Demers
S Demers
228Department of Physics, Yale University, New Haven, CT USA
228,
M Demichev
M Demichev
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
A Demilly
A Demilly
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
S P Denisov
S P Denisov
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
D Denysiuk
D Denysiuk
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
D Derendarz
D Derendarz
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
J E Derkaoui
J E Derkaoui
180Faculté des Sciences, Université Mohamed Premier and LPTPM, Oujda, Morocco
180,
F Derue
F Derue
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
P Dervan
P Dervan
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
K Desch
K Desch
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
C Deterre
C Deterre
65DESY, Hamburg and Zeuthen, Germany
65,
K Dette
K Dette
66Lehrstuhl für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
66,
P O Deviveiros
P O Deviveiros
45CERN, Geneva, Switzerland
45,
A Dewhurst
A Dewhurst
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
S Dhaliwal
S Dhaliwal
31Department of Physics, Brandeis University, Waltham, MA USA
31,
A Di Ciaccio
A Di Ciaccio
173INFN Sezione di Roma Tor Vergata, Rome, Italy
174Dipartimento di Fisica, Università di Roma Tor Vergata, Rome, Italy
173,174,
L Di Ciaccio
L Di Ciaccio
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
W K Di Clemente
W K Di Clemente
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
C Di Donato
C Di Donato
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
A Di Girolamo
A Di Girolamo
45CERN, Geneva, Switzerland
45,
B Di Girolamo
B Di Girolamo
45CERN, Geneva, Switzerland
45,
B Di Micco
B Di Micco
175INFN Sezione di Roma Tre, Rome, Italy
176Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
175,176,
R Di Nardo
R Di Nardo
45CERN, Geneva, Switzerland
45,
A Di Simone
A Di Simone
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
R Di Sipio
R Di Sipio
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
D Di Valentino
D Di Valentino
44Department of Physics, Carleton University, Ottawa, ON Canada
44,
C Diaconu
C Diaconu
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
M Diamond
M Diamond
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
F A Dias
F A Dias
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
M A Diaz
M A Diaz
47Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
47,
E B Diehl
E B Diehl
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
J Dietrich
J Dietrich
19Department of Physics, Humboldt University, Berlin, Germany
19,
S Diglio
S Diglio
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
A Dimitrievska
A Dimitrievska
16Institute of Physics, University of Belgrade, Belgrade, Serbia
16,
J Dingfelder
J Dingfelder
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
P Dita
P Dita
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
S Dita
S Dita
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
F Dittus
F Dittus
45CERN, Geneva, Switzerland
45,
F Djama
F Djama
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
T Djobava
T Djobava
76High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
76,
J I Djuvsland
J I Djuvsland
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
M A B do Vale
M A B do Vale
34Federal University of Sao Joao del Rei (UFSJ), São João del Rei, Brazil
34,
D Dobos
D Dobos
45CERN, Geneva, Switzerland
45,
M Dobre
M Dobre
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
C Doglioni
C Doglioni
111Fysiska institutionen, Lunds universitet, Lund, Sweden
111,
T Dohmae
T Dohmae
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
J Dolejsi
J Dolejsi
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
Z Dolezal
Z Dolezal
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
B A Dolgoshein
B A Dolgoshein
1Department of Physics, University of Adelaide, Adelaide, Australia
128National Research Nuclear University MEPhI, Moscow, Russia
1,128,
M Donadelli
M Donadelli
35Instituto de Fisica, Universidade de Sao Paulo, São Paulo, Brazil
35,
S Donati
S Donati
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
P Dondero
P Dondero
152INFN Sezione di Pavia, Pavia, Italy
153Dipartimento di Fisica, Università di Pavia, Pavia, Italy
152,153,
J Donini
J Donini
55Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
55,
J Dopke
J Dopke
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
A Doria
A Doria
134INFN Sezione di Napoli, Naples, Italy
134,
M T Dova
M T Dova
100Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
100,
A T Doyle
A T Doyle
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
E Drechsler
E Drechsler
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
M Dris
M Dris
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
Y Du
Y Du
52School of Physics, Shandong University, Shandong, China
52,
J Duarte-Campderros
J Duarte-Campderros
203Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
203,
E Duchovni
E Duchovni
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
G Duckeck
G Duckeck
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
O A Ducu
O A Ducu
125Group of Particle Physics, University of Montreal, Montreal, QC Canada
125,
D Duda
D Duda
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
A Dudarev
A Dudarev
45CERN, Geneva, Switzerland
45,
E M Duffield
E M Duffield
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
L Duflot
L Duflot
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
L Duguid
L Duguid
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
M Dührssen
M Dührssen
45CERN, Geneva, Switzerland
45,
M Dumancic
M Dumancic
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
M Dunford
M Dunford
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
H Duran Yildiz
H Duran Yildiz
4Department of Physics, Ankara University, Ankara, Turkey
4,
M Düren
M Düren
77II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
77,
A Durglishvili
A Durglishvili
76High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
76,
D Duschinger
D Duschinger
67Institut für Kern–und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
67,
B Dutta
B Dutta
65DESY, Hamburg and Zeuthen, Germany
65,
M Dyndal
M Dyndal
65DESY, Hamburg and Zeuthen, Germany
65,
C Eckardt
C Eckardt
65DESY, Hamburg and Zeuthen, Germany
65,
K M Ecker
K M Ecker
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
R C Edgar
R C Edgar
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
N C Edwards
N C Edwards
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
T Eifert
T Eifert
45CERN, Geneva, Switzerland
45,
G Eigen
G Eigen
17Department for Physics and Technology, University of Bergen, Bergen, Norway
17,
K Einsweiler
K Einsweiler
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
T Ekelof
T Ekelof
217Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
217,
M El Kacimi
M El Kacimi
179Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakesh, Morocco
179,
V Ellajosyula
V Ellajosyula
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
M Ellert
M Ellert
217Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
217,
S Elles
S Elles
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
F Ellinghaus
F Ellinghaus
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
A A Elliot
A A Elliot
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
N Ellis
N Ellis
45CERN, Geneva, Switzerland
45,
J Elmsheuser
J Elmsheuser
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
M Elsing
M Elsing
45CERN, Geneva, Switzerland
45,
D Emeliyanov
D Emeliyanov
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
Y Enari
Y Enari
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
O C Endner
O C Endner
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
M Endo
M Endo
149Graduate School of Science, Osaka University, Osaka, Japan
149,
J S Ennis
J S Ennis
222Department of Physics, University of Warwick, Coventry, UK
222,
J Erdmann
J Erdmann
66Lehrstuhl für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
66,
A Ereditato
A Ereditato
20Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
20,
G Ernis
G Ernis
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
J Ernst
J Ernst
2Physics Department, SUNY Albany, Albany, NY USA
2,
M Ernst
M Ernst
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
S Errede
S Errede
218Department of Physics, University of Illinois, Urbana, IL USA
218,
E Ertel
E Ertel
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
M Escalier
M Escalier
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
H Esch
H Esch
66Lehrstuhl für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
66,
C Escobar
C Escobar
158Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
158,
B Esposito
B Esposito
70INFN Laboratori Nazionali di Frascati, Frascati, Italy
70,
A I Etienvre
A I Etienvre
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
E Etzion
E Etzion
203Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
203,
H Evans
H Evans
90Department of Physics, Indiana University, Bloomington, IN USA
90,
A Ezhilov
A Ezhilov
155National Research Centre “Kurchatov Institute” B.P. Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
155,
F Fabbri
F Fabbri
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
L Fabbri
L Fabbri
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
G Facini
G Facini
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
R M Fakhrutdinov
R M Fakhrutdinov
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
S Falciano
S Falciano
171INFN Sezione di Roma, Rome, Italy
171,
R J Falla
R J Falla
108Department of Physics and Astronomy, University College London, London, UK
108,
J Faltova
J Faltova
45CERN, Geneva, Switzerland
45,
Y Fang
Y Fang
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
M Fanti
M Fanti
121INFN Sezione di Milano, Milan, Italy
122Dipartimento di Fisica, Università di Milano, Milan, Italy
121,122,
A Farbin
A Farbin
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
A Farilla
A Farilla
175INFN Sezione di Roma Tre, Rome, Italy
175,
C Farina
C Farina
158Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
158,
T Farooque
T Farooque
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
S Farrell
S Farrell
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
S M Farrington
S M Farrington
222Department of Physics, University of Warwick, Coventry, UK
222,
P Farthouat
P Farthouat
45CERN, Geneva, Switzerland
45,
F Fassi
F Fassi
181Faculté des , Sciences, Université Mohammed V, Rabat, Morocco
181,
P Fassnacht
P Fassnacht
45CERN, Geneva, Switzerland
45,
D Fassouliotis
D Fassouliotis
11Physics Department, University of Athens, Athens, Greece
11,
M Faucci Giannelli
M Faucci Giannelli
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
A Favareto
A Favareto
73INFN Sezione di Genova, Genoa, Italy
74Dipartimento di Fisica, Università di Genova, Genoa, Italy
73,74,
W J Fawcett
W J Fawcett
151Department of Physics, Oxford University, Oxford, UK
151,
L Fayard
L Fayard
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
O L Fedin
O L Fedin
155National Research Centre “Kurchatov Institute” B.P. Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
155,
W Fedorko
W Fedorko
220Department of Physics, University of British Columbia, Vancouver, BC Canada
220,
S Feigl
S Feigl
150Department of Physics, University of Oslo, Oslo, Norway
150,
L Feligioni
L Feligioni
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
C Feng
C Feng
52School of Physics, Shandong University, Shandong, China
52,
E J Feng
E J Feng
45CERN, Geneva, Switzerland
45,
H Feng
H Feng
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
A B Fenyuk
A B Fenyuk
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
L Feremenga
L Feremenga
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
P Fernandez Martinez
P Fernandez Martinez
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
S Fernandez Perez
S Fernandez Perez
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
J Ferrando
J Ferrando
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
A Ferrari
A Ferrari
217Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
217,
P Ferrari
P Ferrari
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
R Ferrari
R Ferrari
152INFN Sezione di Pavia, Pavia, Italy
152,
D E Ferreira de Lima
D E Ferreira de Lima
84Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
84,
A Ferrer
A Ferrer
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
D Ferrere
D Ferrere
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
C Ferretti
C Ferretti
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
A Ferretto Parodi
A Ferretto Parodi
73INFN Sezione di Genova, Genoa, Italy
74Dipartimento di Fisica, Università di Genova, Genoa, Italy
73,74,
F Fiedler
F Fiedler
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
A Filipčič
A Filipčič
105Department of Physics, Jožef Stefan Institute, University of Ljubljana, Ljubljana, Slovenia
105,
M Filipuzzi
M Filipuzzi
65DESY, Hamburg and Zeuthen, Germany
65,
F Filthaut
F Filthaut
137Institute for Mathematics Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
137,
M Fincke-Keeler
M Fincke-Keeler
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
K D Finelli
K D Finelli
200School of Physics, University of Sydney, Sydney, Australia
200,
M C N Fiolhais
M C N Fiolhais
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
161Department of Physics, University of Coimbra, Coimbra, Portugal
159,161,
L Fiorini
L Fiorini
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
A Firan
A Firan
63Physics Department, Southern Methodist University, Dallas, TX USA
63,
A Fischer
A Fischer
2Physics Department, SUNY Albany, Albany, NY USA
2,
C Fischer
C Fischer
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
J Fischer
J Fischer
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
W C Fisher
W C Fisher
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
N Flaschel
N Flaschel
65DESY, Hamburg and Zeuthen, Germany
65,
I Fleck
I Fleck
187Fachbereich Physik, Universität Siegen, Siegen, Germany
187,
P Fleischmann
P Fleischmann
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
G T Fletcher
G T Fletcher
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
R R M Fletcher
R R M Fletcher
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
T Flick
T Flick
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
A Floderus
A Floderus
111Fysiska institutionen, Lunds universitet, Lund, Sweden
111,
L R Flores Castillo
L R Flores Castillo
87Department of Physics, The Chinese University of Hong Kong, Shatin, NT Hong Kong
87,
M J Flowerdew
M J Flowerdew
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
G T Forcolin
G T Forcolin
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
A Formica
A Formica
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
A Forti
A Forti
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
A G Foster
A G Foster
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
D Fournier
D Fournier
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
H Fox
H Fox
101Physics Department, Lancaster University, Lancaster, UK
101,
S Fracchia
S Fracchia
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
P Francavilla
P Francavilla
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
M Franchini
M Franchini
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
D Francis
D Francis
45CERN, Geneva, Switzerland
45,
L Franconi
L Franconi
150Department of Physics, University of Oslo, Oslo, Norway
150,
M Franklin
M Franklin
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
M Frate
M Frate
213Department of Physics and Astronomy, University of California Irvine, Irvine, CA USA
213,
M Fraternali
M Fraternali
152INFN Sezione di Pavia, Pavia, Italy
153Dipartimento di Fisica, Università di Pavia, Pavia, Italy
152,153,
D Freeborn
D Freeborn
108Department of Physics and Astronomy, University College London, London, UK
108,
S M Fressard-Batraneanu
S M Fressard-Batraneanu
45CERN, Geneva, Switzerland
45,
F Friedrich
F Friedrich
67Institut für Kern–und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
67,
D Froidevaux
D Froidevaux
45CERN, Geneva, Switzerland
45,
J A Frost
J A Frost
151Department of Physics, Oxford University, Oxford, UK
151,
C Fukunaga
C Fukunaga
206Graduate School of Science and Technology, Tokyo Metropolitan University, Tokyo, Japan
206,
E Fullana Torregrosa
E Fullana Torregrosa
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
T Fusayasu
T Fusayasu
132Nagasaki Institute of Applied Science, Nagasaki, Japan
132,
J Fuster
J Fuster
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
C Gabaldon
C Gabaldon
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
O Gabizon
O Gabizon
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
A Gabrielli
A Gabrielli
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
A Gabrielli
A Gabrielli
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
G P Gach
G P Gach
60AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Kraków, Poland
60,
S Gadatsch
S Gadatsch
45CERN, Geneva, Switzerland
45,
S Gadomski
S Gadomski
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
G Gagliardi
G Gagliardi
73INFN Sezione di Genova, Genoa, Italy
74Dipartimento di Fisica, Università di Genova, Genoa, Italy
73,74,
L G Gagnon
L G Gagnon
125Group of Particle Physics, University of Montreal, Montreal, QC Canada
125,
P Gagnon
P Gagnon
90Department of Physics, Indiana University, Bloomington, IN USA
90,
C Galea
C Galea
137Institute for Mathematics Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
137,
B Galhardo
B Galhardo
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
161Department of Physics, University of Coimbra, Coimbra, Portugal
159,161,
E J Gallas
E J Gallas
151Department of Physics, Oxford University, Oxford, UK
151,
B J Gallop
B J Gallop
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
P Gallus
P Gallus
167Czech Technical University in Prague, Prague, Czech Republic
167,
G Galster
G Galster
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
K K Gan
K K Gan
142Ohio State University, Columbus, OH USA
142,
J Gao
J Gao
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
50,115,
Y Gao
Y Gao
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
Y S Gao
Y S Gao
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
F M Garay Walls
F M Garay Walls
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
C García
C García
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
J E García Navarro
J E García Navarro
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
M Garcia-Sciveres
M Garcia-Sciveres
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
R W Gardner
R W Gardner
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
N Garelli
N Garelli
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
V Garonne
V Garonne
150Department of Physics, University of Oslo, Oslo, Norway
150,
A Gascon Bravo
A Gascon Bravo
65DESY, Hamburg and Zeuthen, Germany
65,
C Gatti
C Gatti
70INFN Laboratori Nazionali di Frascati, Frascati, Italy
70,
A Gaudiello
A Gaudiello
73INFN Sezione di Genova, Genoa, Italy
74Dipartimento di Fisica, Università di Genova, Genoa, Italy
73,74,
G Gaudio
G Gaudio
152INFN Sezione di Pavia, Pavia, Italy
152,
B Gaur
B Gaur
187Fachbereich Physik, Universität Siegen, Siegen, Germany
187,
L Gauthier
L Gauthier
125Group of Particle Physics, University of Montreal, Montreal, QC Canada
125,
I L Gavrilenko
I L Gavrilenko
126P.N. Lebedev Physical Institute of the Russian, Academy of Sciences, Moscow, Russia
126,
C Gay
C Gay
220Department of Physics, University of British Columbia, Vancouver, BC Canada
220,
G Gaycken
G Gaycken
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
E N Gazis
E N Gazis
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
Z Gecse
Z Gecse
220Department of Physics, University of British Columbia, Vancouver, BC Canada
220,
C N P Gee
C N P Gee
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
Ch Geich-Gimbel
Ch Geich-Gimbel
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
M Geisen
M Geisen
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
M P Geisler
M P Geisler
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
C Gemme
C Gemme
73INFN Sezione di Genova, Genoa, Italy
73,
M H Genest
M H Genest
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
C Geng
C Geng
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
S Gentile
S Gentile
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
S George
S George
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
D Gerbaudo
D Gerbaudo
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
A Gershon
A Gershon
203Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
203,
S Ghasemi
S Ghasemi
187Fachbereich Physik, Universität Siegen, Siegen, Germany
187,
H Ghazlane
H Ghazlane
178Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
178,
M Ghneimat
M Ghneimat
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
B Giacobbe
B Giacobbe
27INFN Sezione di Bologna, Bologna, Italy
27,
S Giagu
S Giagu
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
P Giannetti
P Giannetti
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
B Gibbard
B Gibbard
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
S M Gibson
S M Gibson
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
M Gignac
M Gignac
220Department of Physics, University of British Columbia, Vancouver, BC Canada
220,
M Gilchriese
M Gilchriese
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
T P S Gillam
T P S Gillam
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
D Gillberg
D Gillberg
44Department of Physics, Carleton University, Ottawa, ON Canada
44,
G Gilles
G Gilles
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
D M Gingrich
D M Gingrich
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
N Giokaris
N Giokaris
11Physics Department, University of Athens, Athens, Greece
11,
M P Giordani
M P Giordani
214INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
216Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
214,216,
F M Giorgi
F M Giorgi
27INFN Sezione di Bologna, Bologna, Italy
27,
F M Giorgi
F M Giorgi
19Department of Physics, Humboldt University, Berlin, Germany
19,
P F Giraud
P F Giraud
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
P Giromini
P Giromini
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
D Giugni
D Giugni
121INFN Sezione di Milano, Milan, Italy
121,
F Giuli
F Giuli
151Department of Physics, Oxford University, Oxford, UK
151,
C Giuliani
C Giuliani
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
M Giulini
M Giulini
84Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
84,
B K Gjelsten
B K Gjelsten
150Department of Physics, University of Oslo, Oslo, Norway
150,
S Gkaitatzis
S Gkaitatzis
204Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
204,
I Gkialas
I Gkialas
204Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
204,
E L Gkougkousis
E L Gkougkousis
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
L K Gladilin
L K Gladilin
129D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
129,
C Glasman
C Glasman
112Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
112,
J Glatzer
J Glatzer
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
P C F Glaysher
P C F Glaysher
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
A Glazov
A Glazov
65DESY, Hamburg and Zeuthen, Germany
65,
M Goblirsch-Kolb
M Goblirsch-Kolb
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
J Godlewski
J Godlewski
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
S Goldfarb
S Goldfarb
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
T Golling
T Golling
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
D Golubkov
D Golubkov
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
A Gomes
A Gomes
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
160Faculdade de Ciências, Universidade de Lisboa, Lisbon, Portugal
162Centro de Física Nuclear da Universidade de Lisboa, Lisbon, Portugal
159,160,162,
R Gonçalo
R Gonçalo
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
159,
J Goncalves Pinto Firmino Da Costa
J Goncalves Pinto Firmino Da Costa
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
G Gonella
G Gonella
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
L Gonella
L Gonella
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
A Gongadze
A Gongadze
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
S González de la Hoz
S González de la Hoz
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
G Gonzalez Parra
G Gonzalez Parra
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
S Gonzalez-Sevilla
S Gonzalez-Sevilla
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
L Goossens
L Goossens
45CERN, Geneva, Switzerland
45,
P A Gorbounov
P A Gorbounov
127Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
127,
H A Gordon
H A Gordon
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
I Gorelov
I Gorelov
136Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
136,
B Gorini
B Gorini
45CERN, Geneva, Switzerland
45,
E Gorini
E Gorini
102INFN Sezione di Lecce, Lecce, Italy
103Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
102,103,
A Gorišek
A Gorišek
105Department of Physics, Jožef Stefan Institute, University of Ljubljana, Ljubljana, Slovenia
105,
E Gornicki
E Gornicki
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
A T Goshaw
A T Goshaw
68Department of Physics, Duke University, Durham, NC USA
68,
C Gössling
C Gössling
66Lehrstuhl für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
66,
M I Gostkin
M I Gostkin
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
C R Goudet
C R Goudet
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
D Goujdami
D Goujdami
179Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakesh, Morocco
179,
A G Goussiou
A G Goussiou
184Department of Physics, University of Washington, Seattle, WA USA
184,
N Govender
N Govender
193Department of Physics, University of Johannesburg, Johannesburg, South Africa
193,
E Gozani
E Gozani
202Department of Physics, Technion: Israel Institute of Technology, Haifa, Israel
202,
L Graber
L Graber
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
I Grabowska-Bold
I Grabowska-Bold
60AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Kraków, Poland
60,
P O J Gradin
P O J Gradin
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
P Grafström
P Grafström
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
J Gramling
J Gramling
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
E Gramstad
E Gramstad
150Department of Physics, University of Oslo, Oslo, Norway
150,
S Grancagnolo
S Grancagnolo
19Department of Physics, Humboldt University, Berlin, Germany
19,
V Gratchev
V Gratchev
155National Research Centre “Kurchatov Institute” B.P. Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
155,
P M Gravila
P M Gravila
41West University in Timisoara, Timisoara, Romania
41,
H M Gray
H M Gray
45CERN, Geneva, Switzerland
45,
E Graziani
E Graziani
175INFN Sezione di Roma Tre, Rome, Italy
175,
Z D Greenwood
Z D Greenwood
109Louisiana Tech University, Ruston, LA USA
109,
C Grefe
C Grefe
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
K Gregersen
K Gregersen
108Department of Physics and Astronomy, University College London, London, UK
108,
I M Gregor
I M Gregor
65DESY, Hamburg and Zeuthen, Germany
65,
P Grenier
P Grenier
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
K Grevtsov
K Grevtsov
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
J Griffiths
J Griffiths
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
A A Grillo
A A Grillo
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
K Grimm
K Grimm
101Physics Department, Lancaster University, Lancaster, UK
101,
S Grinstein
S Grinstein
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
Ph Gris
Ph Gris
55Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
55,
J -F Grivaz
J -F Grivaz
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
S Groh
S Groh
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
J P Grohs
J P Grohs
67Institut für Kern–und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
67,
E Gross
E Gross
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
J Grosse-Knetter
J Grosse-Knetter
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
G C Grossi
G C Grossi
109Louisiana Tech University, Ruston, LA USA
109,
Z J Grout
Z J Grout
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
L Guan
L Guan
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
W Guan
W Guan
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
J Guenther
J Guenther
167Czech Technical University in Prague, Prague, Czech Republic
167,
F Guescini
F Guescini
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
D Guest
D Guest
213Department of Physics and Astronomy, University of California Irvine, Irvine, CA USA
213,
O Gueta
O Gueta
203Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
203,
E Guido
E Guido
73INFN Sezione di Genova, Genoa, Italy
74Dipartimento di Fisica, Università di Genova, Genoa, Italy
73,74,
T Guillemin
T Guillemin
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
S Guindon
S Guindon
2Physics Department, SUNY Albany, Albany, NY USA
2,
U Gul
U Gul
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
C Gumpert
C Gumpert
45CERN, Geneva, Switzerland
45,
J Guo
J Guo
53Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University (also affiliated with PKU-CHEP), Shanghai, China
53,
Y Guo
Y Guo
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
S Gupta
S Gupta
151Department of Physics, Oxford University, Oxford, UK
151,
G Gustavino
G Gustavino
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
P Gutierrez
P Gutierrez
144Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
144,
N G Gutierrez Ortiz
N G Gutierrez Ortiz
108Department of Physics and Astronomy, University College London, London, UK
108,
C Gutschow
C Gutschow
67Institut für Kern–und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
67,
C Guyot
C Guyot
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
C Gwenlan
C Gwenlan
151Department of Physics, Oxford University, Oxford, UK
151,
C B Gwilliam
C B Gwilliam
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
A Haas
A Haas
141Department of Physics, New York University, New York, NY USA
141,
C Haber
C Haber
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
H K Hadavand
H K Hadavand
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
N Haddad
N Haddad
181Faculté des , Sciences, Université Mohammed V, Rabat, Morocco
181,
A Hadef
A Hadef
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
P Haefner
P Haefner
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
S Hageböck
S Hageböck
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
Z Hajduk
Z Hajduk
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
H Hakobyan
H Hakobyan
1Department of Physics, University of Adelaide, Adelaide, Australia
229Yerevan Physics Institute, Yerevan, Armenia
1,229,
M Haleem
M Haleem
65DESY, Hamburg and Zeuthen, Germany
65,
J Haley
J Haley
145Department of Physics, Oklahoma State University, Stillwater, OK USA
145,
G Halladjian
G Halladjian
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
G D Hallewell
G D Hallewell
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
K Hamacher
K Hamacher
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
P Hamal
P Hamal
146Palacký University, RCPTM, Olomouc, Czech Republic
146,
K Hamano
K Hamano
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
A Hamilton
A Hamilton
192Department of Physics, University of Cape Town, Cape Town, South Africa
192,
G N Hamity
G N Hamity
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
P G Hamnett
P G Hamnett
65DESY, Hamburg and Zeuthen, Germany
65,
L Han
L Han
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
K Hanagaki
K Hanagaki
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
K Hanawa
K Hanawa
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
M Hance
M Hance
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
B Haney
B Haney
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
P Hanke
P Hanke
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
R Hanna
R Hanna
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
J B Hansen
J B Hansen
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
J D Hansen
J D Hansen
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
M C Hansen
M C Hansen
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
P H Hansen
P H Hansen
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
K Hara
K Hara
211Faculty of Pure and Applied Sciences, and Center for Integrated Research in Fundamental Science and Engineering, University of Tsukuba, Tsukuba, Japan
211,
A S Hard
A S Hard
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
T Harenberg
T Harenberg
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
F Hariri
F Hariri
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
S Harkusha
S Harkusha
123B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
123,
R D Harrington
R D Harrington
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
P F Harrison
P F Harrison
222Department of Physics, University of Warwick, Coventry, UK
222,
F Hartjes
F Hartjes
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
N M Hartmann
N M Hartmann
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
M Hasegawa
M Hasegawa
96Graduate School of Science, Kobe University, Kobe, Japan
96,
Y Hasegawa
Y Hasegawa
186Department of Physics, Shinshu University, Nagano, Japan
186,
A Hasib
A Hasib
144Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
144,
S Hassani
S Hassani
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
S Haug
S Haug
20Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
20,
R Hauser
R Hauser
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
L Hauswald
L Hauswald
67Institut für Kern–und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
67,
M Havranek
M Havranek
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
C M Hawkes
C M Hawkes
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
R J Hawkings
R J Hawkings
45CERN, Geneva, Switzerland
45,
D Hayden
D Hayden
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
C P Hays
C P Hays
151Department of Physics, Oxford University, Oxford, UK
151,
J M Hays
J M Hays
106School of Physics and Astronomy, Queen Mary University of London, London, UK
106,
H S Hayward
H S Hayward
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
S J Haywood
S J Haywood
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
S J Head
S J Head
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
T Heck
T Heck
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
V Hedberg
V Hedberg
111Fysiska institutionen, Lunds universitet, Lund, Sweden
111,
L Heelan
L Heelan
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
S Heim
S Heim
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
T Heim
T Heim
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
B Heinemann
B Heinemann
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
J J Heinrich
J J Heinrich
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
L Heinrich
L Heinrich
141Department of Physics, New York University, New York, NY USA
141,
C Heinz
C Heinz
77II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
77,
J Hejbal
J Hejbal
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
L Helary
L Helary
30Department of Physics, Boston University, Boston, MA USA
30,
S Hellman
S Hellman
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
C Helsens
C Helsens
45CERN, Geneva, Switzerland
45,
J Henderson
J Henderson
151Department of Physics, Oxford University, Oxford, UK
151,
R C W Henderson
R C W Henderson
101Physics Department, Lancaster University, Lancaster, UK
101,
Y Heng
Y Heng
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
S Henkelmann
S Henkelmann
220Department of Physics, University of British Columbia, Vancouver, BC Canada
220,
A M Henriques Correia
A M Henriques Correia
45CERN, Geneva, Switzerland
45,
S Henrot-Versille
S Henrot-Versille
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
G H Herbert
G H Herbert
19Department of Physics, Humboldt University, Berlin, Germany
19,
Y Hernández Jiménez
Y Hernández Jiménez
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
G Herten
G Herten
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
R Hertenberger
R Hertenberger
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
L Hervas
L Hervas
45CERN, Geneva, Switzerland
45,
G G Hesketh
G G Hesketh
108Department of Physics and Astronomy, University College London, London, UK
108,
N P Hessey
N P Hessey
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
J W Hetherly
J W Hetherly
63Physics Department, Southern Methodist University, Dallas, TX USA
63,
R Hickling
R Hickling
106School of Physics and Astronomy, Queen Mary University of London, London, UK
106,
E Higón-Rodriguez
E Higón-Rodriguez
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
E Hill
E Hill
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
J C Hill
J C Hill
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
K H Hiller
K H Hiller
65DESY, Hamburg and Zeuthen, Germany
65,
S J Hillier
S J Hillier
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
I Hinchliffe
I Hinchliffe
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
E Hines
E Hines
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
R R Hinman
R R Hinman
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
M Hirose
M Hirose
207Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
207,
D Hirschbuehl
D Hirschbuehl
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
J Hobbs
J Hobbs
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
N Hod
N Hod
209TRIUMF, Vancouver, BC Canada
209,
M C Hodgkinson
M C Hodgkinson
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
P Hodgson
P Hodgson
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
A Hoecker
A Hoecker
45CERN, Geneva, Switzerland
45,
M R Hoeferkamp
M R Hoeferkamp
136Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
136,
F Hoenig
F Hoenig
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
D Hohn
D Hohn
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
T R Holmes
T R Holmes
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
M Homann
M Homann
66Lehrstuhl für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
66,
T M Hong
T M Hong
158Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
158,
B H Hooberman
B H Hooberman
218Department of Physics, University of Illinois, Urbana, IL USA
218,
W H Hopkins
W H Hopkins
147Center for High Energy Physics, University of Oregon, Eugene, OR USA
147,
Y Horii
Y Horii
133Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
133,
A J Horton
A J Horton
188Department of Physics, Simon Fraser University, Burnaby, BC Canada
188,
J-Y Hostachy
J-Y Hostachy
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
S Hou
S Hou
201Institute of Physics, Academia Sinica, Taipei, Taiwan
201,
A Hoummada
A Hoummada
177Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies-Université Hassan II, Casablanca, Morocco
177,
J Howarth
J Howarth
65DESY, Hamburg and Zeuthen, Germany
65,
M Hrabovsky
M Hrabovsky
146Palacký University, RCPTM, Olomouc, Czech Republic
146,
I Hristova
I Hristova
19Department of Physics, Humboldt University, Berlin, Germany
19,
J Hrivnac
J Hrivnac
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
T Hryn’ova
T Hryn’ova
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
A Hrynevich
A Hrynevich
124National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
124,
C Hsu
C Hsu
194School of Physics, University of the Witwatersrand, Johannesburg, South Africa
194,
P J Hsu
P J Hsu
201Institute of Physics, Academia Sinica, Taipei, Taiwan
201,
S -C Hsu
S -C Hsu
184Department of Physics, University of Washington, Seattle, WA USA
184,
D Hu
D Hu
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
Q Hu
Q Hu
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
Y Huang
Y Huang
65DESY, Hamburg and Zeuthen, Germany
65,
Z Hubacek
Z Hubacek
167Czech Technical University in Prague, Prague, Czech Republic
167,
F Hubaut
F Hubaut
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
F Huegging
F Huegging
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
T B Huffman
T B Huffman
151Department of Physics, Oxford University, Oxford, UK
151,
E W Hughes
E W Hughes
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
G Hughes
G Hughes
101Physics Department, Lancaster University, Lancaster, UK
101,
M Huhtinen
M Huhtinen
45CERN, Geneva, Switzerland
45,
T A Hülsing
T A Hülsing
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
P Huo
P Huo
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
N Huseynov
N Huseynov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
J Huston
J Huston
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
J Huth
J Huth
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
G Iacobucci
G Iacobucci
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
G Iakovidis
G Iakovidis
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
I Ibragimov
I Ibragimov
187Fachbereich Physik, Universität Siegen, Siegen, Germany
187,
L Iconomidou-Fayard
L Iconomidou-Fayard
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
E Ideal
E Ideal
228Department of Physics, Yale University, New Haven, CT USA
228,
Z Idrissi
Z Idrissi
181Faculté des , Sciences, Université Mohammed V, Rabat, Morocco
181,
P Iengo
P Iengo
45CERN, Geneva, Switzerland
45,
O Igonkina
O Igonkina
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
T Iizawa
T Iizawa
223Waseda University, Tokyo, Japan
223,
Y Ikegami
Y Ikegami
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
M Ikeno
M Ikeno
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
Y Ilchenko
Y Ilchenko
13Department of Physics, The University of Texas at Austin, Austin, TX USA
13,
D Iliadis
D Iliadis
204Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
204,
N Ilic
N Ilic
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
T Ince
T Ince
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
G Introzzi
G Introzzi
152INFN Sezione di Pavia, Pavia, Italy
153Dipartimento di Fisica, Università di Pavia, Pavia, Italy
152,153,
P Ioannou
P Ioannou
1Department of Physics, University of Adelaide, Adelaide, Australia
11Physics Department, University of Athens, Athens, Greece
1,11,
M Iodice
M Iodice
175INFN Sezione di Roma Tre, Rome, Italy
175,
K Iordanidou
K Iordanidou
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
V Ippolito
V Ippolito
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
M Ishino
M Ishino
97Faculty of Science, Kyoto University, Kyoto, Japan
97,
M Ishitsuka
M Ishitsuka
207Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
207,
R Ishmukhametov
R Ishmukhametov
142Ohio State University, Columbus, OH USA
142,
C Issever
C Issever
151Department of Physics, Oxford University, Oxford, UK
151,
S Istin
S Istin
22Department of Physics, Bogazici University, Istanbul, Turkey
22,
F Ito
F Ito
211Faculty of Pure and Applied Sciences, and Center for Integrated Research in Fundamental Science and Engineering, University of Tsukuba, Tsukuba, Japan
211,
J M Iturbe Ponce
J M Iturbe Ponce
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
R Iuppa
R Iuppa
173INFN Sezione di Roma Tor Vergata, Rome, Italy
174Dipartimento di Fisica, Università di Roma Tor Vergata, Rome, Italy
173,174,
W Iwanski
W Iwanski
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
H Iwasaki
H Iwasaki
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
J M Izen
J M Izen
64Physics Department, University of Texas at Dallas, Richardson, TX USA
64,
V Izzo
V Izzo
134INFN Sezione di Napoli, Naples, Italy
134,
S Jabbar
S Jabbar
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
B Jackson
B Jackson
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
M Jackson
M Jackson
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
P Jackson
P Jackson
1Department of Physics, University of Adelaide, Adelaide, Australia
1,
V Jain
V Jain
2Physics Department, SUNY Albany, Albany, NY USA
2,
K B Jakobi
K B Jakobi
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
K Jakobs
K Jakobs
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
S Jakobsen
S Jakobsen
45CERN, Geneva, Switzerland
45,
T Jakoubek
T Jakoubek
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
D O Jamin
D O Jamin
145Department of Physics, Oklahoma State University, Stillwater, OK USA
145,
D K Jana
D K Jana
109Louisiana Tech University, Ruston, LA USA
109,
E Jansen
E Jansen
108Department of Physics and Astronomy, University College London, London, UK
108,
R Jansky
R Jansky
91Institut für Astro–und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
91,
J Janssen
J Janssen
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
M Janus
M Janus
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
G Jarlskog
G Jarlskog
111Fysiska institutionen, Lunds universitet, Lund, Sweden
111,
N Javadov
N Javadov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
T Javůrek
T Javůrek
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
F Jeanneau
F Jeanneau
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
L Jeanty
L Jeanty
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
J Jejelava
J Jejelava
75E. Andronikashvili Institute of Physics, Iv. Javakhishvili Tbilisi State University, Tbilisi, Georgia
75,
G -Y Jeng
G -Y Jeng
200School of Physics, University of Sydney, Sydney, Australia
200,
D Jennens
D Jennens
118School of Physics, University of Melbourne, Victoria, Australia
118,
P Jenni
P Jenni
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
J Jentzsch
J Jentzsch
66Lehrstuhl für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
66,
C Jeske
C Jeske
222Department of Physics, University of Warwick, Coventry, UK
222,
S Jézéquel
S Jézéquel
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
H Ji
H Ji
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
J Jia
J Jia
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
H Jiang
H Jiang
93Department of Physics and Astronomy, Iowa State University, Ames, IA USA
93,
Y Jiang
Y Jiang
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
S Jiggins
S Jiggins
108Department of Physics and Astronomy, University College London, London, UK
108,
J Jimenez Pena
J Jimenez Pena
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
S Jin
S Jin
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
A Jinaru
A Jinaru
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
O Jinnouchi
O Jinnouchi
207Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
207,
P Johansson
P Johansson
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
K A Johns
K A Johns
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
W J Johnson
W J Johnson
184Department of Physics, University of Washington, Seattle, WA USA
184,
K Jon-And
K Jon-And
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
G Jones
G Jones
222Department of Physics, University of Warwick, Coventry, UK
222,
R W L Jones
R W L Jones
101Physics Department, Lancaster University, Lancaster, UK
101,
S Jones
S Jones
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
T J Jones
T J Jones
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
J Jongmanns
J Jongmanns
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
P M Jorge
P M Jorge
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
160Faculdade de Ciências, Universidade de Lisboa, Lisbon, Portugal
159,160,
J Jovicevic
J Jovicevic
209TRIUMF, Vancouver, BC Canada
209,
X Ju
X Ju
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
A Juste Rozas
A Juste Rozas
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
M K Köhler
M K Köhler
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
A Kaczmarska
A Kaczmarska
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
M Kado
M Kado
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
H Kagan
H Kagan
142Ohio State University, Columbus, OH USA
142,
M Kagan
M Kagan
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
S J Kahn
S J Kahn
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
E Kajomovitz
E Kajomovitz
68Department of Physics, Duke University, Durham, NC USA
68,
C W Kalderon
C W Kalderon
151Department of Physics, Oxford University, Oxford, UK
151,
A Kaluza
A Kaluza
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
S Kama
S Kama
63Physics Department, Southern Methodist University, Dallas, TX USA
63,
A Kamenshchikov
A Kamenshchikov
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
N Kanaya
N Kanaya
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
S Kaneti
S Kaneti
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
L Kanjir
L Kanjir
105Department of Physics, Jožef Stefan Institute, University of Ljubljana, Ljubljana, Slovenia
105,
V A Kantserov
V A Kantserov
128National Research Nuclear University MEPhI, Moscow, Russia
128,
J Kanzaki
J Kanzaki
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
B Kaplan
B Kaplan
141Department of Physics, New York University, New York, NY USA
141,
L S Kaplan
L S Kaplan
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
A Kapliy
A Kapliy
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
D Kar
D Kar
194School of Physics, University of the Witwatersrand, Johannesburg, South Africa
194,
K Karakostas
K Karakostas
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
A Karamaoun
A Karamaoun
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
N Karastathis
N Karastathis
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
M J Kareem
M J Kareem
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
E Karentzos
E Karentzos
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
M Karnevskiy
M Karnevskiy
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
S N Karpov
S N Karpov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
Z M Karpova
Z M Karpova
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
K Karthik
K Karthik
141Department of Physics, New York University, New York, NY USA
141,
V Kartvelishvili
V Kartvelishvili
101Physics Department, Lancaster University, Lancaster, UK
101,
A N Karyukhin
A N Karyukhin
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
K Kasahara
K Kasahara
211Faculty of Pure and Applied Sciences, and Center for Integrated Research in Fundamental Science and Engineering, University of Tsukuba, Tsukuba, Japan
211,
L Kashif
L Kashif
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
R D Kass
R D Kass
142Ohio State University, Columbus, OH USA
142,
A Kastanas
A Kastanas
17Department for Physics and Technology, University of Bergen, Bergen, Norway
17,
Y Kataoka
Y Kataoka
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
C Kato
C Kato
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
A Katre
A Katre
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
J Katzy
J Katzy
65DESY, Hamburg and Zeuthen, Germany
65,
K Kawagoe
K Kawagoe
99Department of Physics, Kyushu University, Fukuoka, Japan
99,
T Kawamoto
T Kawamoto
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
G Kawamura
G Kawamura
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
S Kazama
S Kazama
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
V F Kazanin
V F Kazanin
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
R Keeler
R Keeler
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
R Kehoe
R Kehoe
63Physics Department, Southern Methodist University, Dallas, TX USA
63,
J S Keller
J S Keller
65DESY, Hamburg and Zeuthen, Germany
65,
J J Kempster
J J Kempster
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
K Kawade
K Kawade
133Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
133,
H Keoshkerian
H Keoshkerian
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
O Kepka
O Kepka
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
B P Kerševan
B P Kerševan
105Department of Physics, Jožef Stefan Institute, University of Ljubljana, Ljubljana, Slovenia
105,
S Kersten
S Kersten
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
R A Keyes
R A Keyes
117Department of Physics, McGill University, Montreal, QC Canada
117,
F Khalil-zada
F Khalil-zada
14Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
14,
A Khanov
A Khanov
145Department of Physics, Oklahoma State University, Stillwater, OK USA
145,
A G Kharlamov
A G Kharlamov
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
T J Khoo
T J Khoo
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
V Khovanskiy
V Khovanskiy
127Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
127,
E Khramov
E Khramov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
J Khubua
J Khubua
76High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
76,
S Kido
S Kido
96Graduate School of Science, Kobe University, Kobe, Japan
96,
H Y Kim
H Y Kim
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
S H Kim
S H Kim
211Faculty of Pure and Applied Sciences, and Center for Integrated Research in Fundamental Science and Engineering, University of Tsukuba, Tsukuba, Japan
211,
Y K Kim
Y K Kim
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
N Kimura
N Kimura
204Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
204,
O M Kind
O M Kind
19Department of Physics, Humboldt University, Berlin, Germany
19,
B T King
B T King
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
M King
M King
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
S B King
S B King
220Department of Physics, University of British Columbia, Vancouver, BC Canada
220,
J Kirk
J Kirk
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
A E Kiryunin
A E Kiryunin
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
T Kishimoto
T Kishimoto
96Graduate School of Science, Kobe University, Kobe, Japan
96,
D Kisielewska
D Kisielewska
60AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Kraków, Poland
60,
F Kiss
F Kiss
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
K Kiuchi
K Kiuchi
211Faculty of Pure and Applied Sciences, and Center for Integrated Research in Fundamental Science and Engineering, University of Tsukuba, Tsukuba, Japan
211,
O Kivernyk
O Kivernyk
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
E Kladiva
E Kladiva
191Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
191,
M H Klein
M H Klein
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
M Klein
M Klein
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
U Klein
U Klein
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
K Kleinknecht
K Kleinknecht
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
P Klimek
P Klimek
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
A Klimentov
A Klimentov
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
R Klingenberg
R Klingenberg
66Lehrstuhl für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
66,
J A Klinger
J A Klinger
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
T Klioutchnikova
T Klioutchnikova
45CERN, Geneva, Switzerland
45,
E -E Kluge
E -E Kluge
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
P Kluit
P Kluit
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
S Kluth
S Kluth
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
J Knapik
J Knapik
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
E Kneringer
E Kneringer
91Institut für Astro–und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
91,
E B F G Knoops
E B F G Knoops
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
A Knue
A Knue
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
A Kobayashi
A Kobayashi
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
D Kobayashi
D Kobayashi
207Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
207,
T Kobayashi
T Kobayashi
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
M Kobel
M Kobel
67Institut für Kern–und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
67,
M Kocian
M Kocian
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
P Kodys
P Kodys
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
T Koffas
T Koffas
44Department of Physics, Carleton University, Ottawa, ON Canada
44,
E Koffeman
E Koffeman
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
T Koi
T Koi
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
H Kolanoski
H Kolanoski
19Department of Physics, Humboldt University, Berlin, Germany
19,
M Kolb
M Kolb
84Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
84,
I Koletsou
I Koletsou
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
A A Komar
A A Komar
1Department of Physics, University of Adelaide, Adelaide, Australia
126P.N. Lebedev Physical Institute of the Russian, Academy of Sciences, Moscow, Russia
1,126,
Y Komori
Y Komori
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
T Kondo
T Kondo
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
N Kondrashova
N Kondrashova
65DESY, Hamburg and Zeuthen, Germany
65,
K Köneke
K Köneke
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
A C König
A C König
137Institute for Mathematics Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
137,
T Kono
T Kono
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
R Konoplich
R Konoplich
141Department of Physics, New York University, New York, NY USA
141,
N Konstantinidis
N Konstantinidis
108Department of Physics and Astronomy, University College London, London, UK
108,
R Kopeliansky
R Kopeliansky
90Department of Physics, Indiana University, Bloomington, IN USA
90,
S Koperny
S Koperny
60AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Kraków, Poland
60,
L Köpke
L Köpke
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
A K Kopp
A K Kopp
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
K Korcyl
K Korcyl
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
K Kordas
K Kordas
204Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
204,
A Korn
A Korn
108Department of Physics and Astronomy, University College London, London, UK
108,
A A Korol
A A Korol
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
I Korolkov
I Korolkov
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
E V Korolkova
E V Korolkova
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
O Kortner
O Kortner
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
S Kortner
S Kortner
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
T Kosek
T Kosek
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
V V Kostyukhin
V V Kostyukhin
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
A Kotwal
A Kotwal
68Department of Physics, Duke University, Durham, NC USA
68,
A Kourkoumeli-Charalampidi
A Kourkoumeli-Charalampidi
204Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
204,
C Kourkoumelis
C Kourkoumelis
11Physics Department, University of Athens, Athens, Greece
11,
V Kouskoura
V Kouskoura
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
A B Kowalewska
A B Kowalewska
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
R Kowalewski
R Kowalewski
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
T Z Kowalski
T Z Kowalski
60AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Kraków, Poland
60,
C Kozakai
C Kozakai
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
W Kozanecki
W Kozanecki
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
A S Kozhin
A S Kozhin
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
V A Kramarenko
V A Kramarenko
129D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
129,
G Kramberger
G Kramberger
105Department of Physics, Jožef Stefan Institute, University of Ljubljana, Ljubljana, Slovenia
105,
D Krasnopevtsev
D Krasnopevtsev
128National Research Nuclear University MEPhI, Moscow, Russia
128,
M W Krasny
M W Krasny
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
A Krasznahorkay
A Krasznahorkay
45CERN, Geneva, Switzerland
45,
J K Kraus
J K Kraus
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
A Kravchenko
A Kravchenko
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
M Kretz
M Kretz
85ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
85,
J Kretzschmar
J Kretzschmar
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
K Kreutzfeldt
K Kreutzfeldt
77II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
77,
P Krieger
P Krieger
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
K Krizka
K Krizka
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
K Kroeninger
K Kroeninger
66Lehrstuhl für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
66,
H Kroha
H Kroha
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
J Kroll
J Kroll
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
J Kroseberg
J Kroseberg
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
J Krstic
J Krstic
16Institute of Physics, University of Belgrade, Belgrade, Serbia
16,
U Kruchonak
U Kruchonak
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
H Krüger
H Krüger
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
N Krumnack
N Krumnack
93Department of Physics and Astronomy, Iowa State University, Ames, IA USA
93,
A Kruse
A Kruse
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
M C Kruse
M C Kruse
68Department of Physics, Duke University, Durham, NC USA
68,
M Kruskal
M Kruskal
30Department of Physics, Boston University, Boston, MA USA
30,
T Kubota
T Kubota
118School of Physics, University of Melbourne, Victoria, Australia
118,
H Kucuk
H Kucuk
108Department of Physics and Astronomy, University College London, London, UK
108,
S Kuday
S Kuday
5Istanbul Aydin University, Istanbul, Turkey
5,
J T Kuechler
J T Kuechler
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
S Kuehn
S Kuehn
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
A Kugel
A Kugel
85ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
85,
F Kuger
F Kuger
226Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
226,
A Kuhl
A Kuhl
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
T Kuhl
T Kuhl
65DESY, Hamburg and Zeuthen, Germany
65,
V Kukhtin
V Kukhtin
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
R Kukla
R Kukla
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
Y Kulchitsky
Y Kulchitsky
123B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
123,
S Kuleshov
S Kuleshov
48Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
48,
M Kuna
M Kuna
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
T Kunigo
T Kunigo
97Faculty of Science, Kyoto University, Kyoto, Japan
97,
A Kupco
A Kupco
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
H Kurashige
H Kurashige
96Graduate School of Science, Kobe University, Kobe, Japan
96,
Y A Kurochkin
Y A Kurochkin
123B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
123,
V Kus
V Kus
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
E S Kuwertz
E S Kuwertz
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
M Kuze
M Kuze
207Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
207,
J Kvita
J Kvita
146Palacký University, RCPTM, Olomouc, Czech Republic
146,
T Kwan
T Kwan
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
D Kyriazopoulos
D Kyriazopoulos
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
A La Rosa
A La Rosa
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
J L La Rosa Navarro
J L La Rosa Navarro
35Instituto de Fisica, Universidade de Sao Paulo, São Paulo, Brazil
35,
L La Rotonda
L La Rotonda
58INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Cosenza, Italy
59Dipartimento di Fisica, Università della Calabria, Rende, Italy
58,59,
C Lacasta
C Lacasta
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
F Lacava
F Lacava
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
J Lacey
J Lacey
44Department of Physics, Carleton University, Ottawa, ON Canada
44,
H Lacker
H Lacker
19Department of Physics, Humboldt University, Berlin, Germany
19,
D Lacour
D Lacour
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
V R Lacuesta
V R Lacuesta
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
E Ladygin
E Ladygin
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
R Lafaye
R Lafaye
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
B Laforge
B Laforge
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
T Lagouri
T Lagouri
228Department of Physics, Yale University, New Haven, CT USA
228,
S Lai
S Lai
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
S Lammers
S Lammers
90Department of Physics, Indiana University, Bloomington, IN USA
90,
W Lampl
W Lampl
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
E Lançon
E Lançon
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
U Landgraf
U Landgraf
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
M P J Landon
M P J Landon
106School of Physics and Astronomy, Queen Mary University of London, London, UK
106,
V S Lang
V S Lang
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
J C Lange
J C Lange
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
A J Lankford
A J Lankford
213Department of Physics and Astronomy, University of California Irvine, Irvine, CA USA
213,
F Lanni
F Lanni
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
K Lantzsch
K Lantzsch
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
A Lanza
A Lanza
152INFN Sezione di Pavia, Pavia, Italy
152,
S Laplace
S Laplace
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
C Lapoire
C Lapoire
45CERN, Geneva, Switzerland
45,
J F Laporte
J F Laporte
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
T Lari
T Lari
121INFN Sezione di Milano, Milan, Italy
121,
F Lasagni Manghi
F Lasagni Manghi
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
M Lassnig
M Lassnig
45CERN, Geneva, Switzerland
45,
P Laurelli
P Laurelli
70INFN Laboratori Nazionali di Frascati, Frascati, Italy
70,
W Lavrijsen
W Lavrijsen
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
A T Law
A T Law
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
P Laycock
P Laycock
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
T Lazovich
T Lazovich
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
M Lazzaroni
M Lazzaroni
121INFN Sezione di Milano, Milan, Italy
122Dipartimento di Fisica, Università di Milano, Milan, Italy
121,122,
B Le
B Le
118School of Physics, University of Melbourne, Victoria, Australia
118,
O Le Dortz
O Le Dortz
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
E Le Guirriec
E Le Guirriec
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
E P Le Quilleuc
E P Le Quilleuc
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
M LeBlanc
M LeBlanc
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
T LeCompte
T LeCompte
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
F Ledroit-Guillon
F Ledroit-Guillon
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
C A Lee
C A Lee
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
S C Lee
S C Lee
201Institute of Physics, Academia Sinica, Taipei, Taiwan
201,
L Lee
L Lee
1Department of Physics, University of Adelaide, Adelaide, Australia
1,
G Lefebvre
G Lefebvre
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
M Lefebvre
M Lefebvre
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
F Legger
F Legger
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
C Leggett
C Leggett
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
A Lehan
A Lehan
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
G Lehmann Miotto
G Lehmann Miotto
45CERN, Geneva, Switzerland
45,
X Lei
X Lei
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
W A Leight
W A Leight
44Department of Physics, Carleton University, Ottawa, ON Canada
44,
A Leisos
A Leisos
204Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
204,
A G Leister
A G Leister
228Department of Physics, Yale University, New Haven, CT USA
228,
M A L Leite
M A L Leite
35Instituto de Fisica, Universidade de Sao Paulo, São Paulo, Brazil
35,
R Leitner
R Leitner
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
D Lellouch
D Lellouch
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
B Lemmer
B Lemmer
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
K J C Leney
K J C Leney
108Department of Physics and Astronomy, University College London, London, UK
108,
T Lenz
T Lenz
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
B Lenzi
B Lenzi
45CERN, Geneva, Switzerland
45,
R Leone
R Leone
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
S Leone
S Leone
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
C Leonidopoulos
C Leonidopoulos
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
S Leontsinis
S Leontsinis
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
G Lerner
G Lerner
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
C Leroy
C Leroy
125Group of Particle Physics, University of Montreal, Montreal, QC Canada
125,
A A J Lesage
A A J Lesage
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
C G Lester
C G Lester
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
M Levchenko
M Levchenko
155National Research Centre “Kurchatov Institute” B.P. Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
155,
J Levêque
J Levêque
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
D Levin
D Levin
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
L J Levinson
L J Levinson
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
M Levy
M Levy
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
D Lewis
D Lewis
106School of Physics and Astronomy, Queen Mary University of London, London, UK
106,
A M Leyko
A M Leyko
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
M Leyton
M Leyton
64Physics Department, University of Texas at Dallas, Richardson, TX USA
64,
B Li
B Li
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
H Li
H Li
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
H L Li
H L Li
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
L Li
L Li
68Department of Physics, Duke University, Durham, NC USA
68,
L Li
L Li
53Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University (also affiliated with PKU-CHEP), Shanghai, China
53,
Q Li
Q Li
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
S Li
S Li
68Department of Physics, Duke University, Durham, NC USA
68,
X Li
X Li
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
Y Li
Y Li
187Fachbereich Physik, Universität Siegen, Siegen, Germany
187,
Z Liang
Z Liang
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
B Liberti
B Liberti
173INFN Sezione di Roma Tor Vergata, Rome, Italy
173,
A Liblong
A Liblong
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
P Lichard
P Lichard
45CERN, Geneva, Switzerland
45,
K Lie
K Lie
218Department of Physics, University of Illinois, Urbana, IL USA
218,
J Liebal
J Liebal
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
W Liebig
W Liebig
17Department for Physics and Technology, University of Bergen, Bergen, Norway
17,
A Limosani
A Limosani
200School of Physics, University of Sydney, Sydney, Australia
200,
S C Lin
S C Lin
201Institute of Physics, Academia Sinica, Taipei, Taiwan
201,
T H Lin
T H Lin
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
B E Lindquist
B E Lindquist
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
A E Lionti
A E Lionti
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
E Lipeles
E Lipeles
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
A Lipniacka
A Lipniacka
17Department for Physics and Technology, University of Bergen, Bergen, Norway
17,
M Lisovyi
M Lisovyi
84Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
84,
T M Liss
T M Liss
218Department of Physics, University of Illinois, Urbana, IL USA
218,
A Lister
A Lister
220Department of Physics, University of British Columbia, Vancouver, BC Canada
220,
A M Litke
A M Litke
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
B Liu
B Liu
201Institute of Physics, Academia Sinica, Taipei, Taiwan
201,
D Liu
D Liu
201Institute of Physics, Academia Sinica, Taipei, Taiwan
201,
H Liu
H Liu
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
H Liu
H Liu
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
J Liu
J Liu
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
J B Liu
J B Liu
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
K Liu
K Liu
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
L Liu
L Liu
218Department of Physics, University of Illinois, Urbana, IL USA
218,
M Liu
M Liu
68Department of Physics, Duke University, Durham, NC USA
68,
M Liu
M Liu
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
Y L Liu
Y L Liu
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
Y Liu
Y Liu
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
M Livan
M Livan
152INFN Sezione di Pavia, Pavia, Italy
153Dipartimento di Fisica, Università di Pavia, Pavia, Italy
152,153,
A Lleres
A Lleres
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
J Llorente Merino
J Llorente Merino
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
S L Lloyd
S L Lloyd
106School of Physics and Astronomy, Queen Mary University of London, London, UK
106,
F Lo Sterzo
F Lo Sterzo
201Institute of Physics, Academia Sinica, Taipei, Taiwan
201,
E Lobodzinska
E Lobodzinska
65DESY, Hamburg and Zeuthen, Germany
65,
P Loch
P Loch
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
W S Lockman
W S Lockman
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
F K Loebinger
F K Loebinger
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
A E Loevschall-Jensen
A E Loevschall-Jensen
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
K M Loew
K M Loew
31Department of Physics, Brandeis University, Waltham, MA USA
31,
A Loginov
A Loginov
1Department of Physics, University of Adelaide, Adelaide, Australia
228Department of Physics, Yale University, New Haven, CT USA
1,228,
T Lohse
T Lohse
19Department of Physics, Humboldt University, Berlin, Germany
19,
K Lohwasser
K Lohwasser
65DESY, Hamburg and Zeuthen, Germany
65,
M Lokajicek
M Lokajicek
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
B A Long
B A Long
30Department of Physics, Boston University, Boston, MA USA
30,
J D Long
J D Long
218Department of Physics, University of Illinois, Urbana, IL USA
218,
R E Long
R E Long
101Physics Department, Lancaster University, Lancaster, UK
101,
L Longo
L Longo
102INFN Sezione di Lecce, Lecce, Italy
103Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
102,103,
K A Looper
K A Looper
142Ohio State University, Columbus, OH USA
142,
L Lopes
L Lopes
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
159,
D Lopez Mateos
D Lopez Mateos
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
B Lopez Paredes
B Lopez Paredes
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
I Lopez Paz
I Lopez Paz
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
A Lopez Solis
A Lopez Solis
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
J Lorenz
J Lorenz
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
N Lorenzo Martinez
N Lorenzo Martinez
90Department of Physics, Indiana University, Bloomington, IN USA
90,
M Losada
M Losada
26Centro de Investigaciones, Universidad Antonio Narino, Bogotá, Colombia
26,
P J Lösel
P J Lösel
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
X Lou
X Lou
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
A Lounis
A Lounis
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
J Love
J Love
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
P A Love
P A Love
101Physics Department, Lancaster University, Lancaster, UK
101,
H Lu
H Lu
87Department of Physics, The Chinese University of Hong Kong, Shatin, NT Hong Kong
87,
N Lu
N Lu
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
H J Lubatti
H J Lubatti
184Department of Physics, University of Washington, Seattle, WA USA
184,
C Luci
C Luci
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
A Lucotte
A Lucotte
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
C Luedtke
C Luedtke
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
F Luehring
F Luehring
90Department of Physics, Indiana University, Bloomington, IN USA
90,
W Lukas
W Lukas
91Institut für Astro–und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
91,
L Luminari
L Luminari
171INFN Sezione di Roma, Rome, Italy
171,
O Lundberg
O Lundberg
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
B Lund-Jensen
B Lund-Jensen
197Physics Department, Royal Institute of Technology, Stockholm, Sweden
197,
P M Luzi
P M Luzi
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
D Lynn
D Lynn
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
R Lysak
R Lysak
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
E Lytken
E Lytken
111Fysiska institutionen, Lunds universitet, Lund, Sweden
111,
V Lyubushkin
V Lyubushkin
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
H Ma
H Ma
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
L L Ma
L L Ma
52School of Physics, Shandong University, Shandong, China
52,
Y Ma
Y Ma
52School of Physics, Shandong University, Shandong, China
52,
G Maccarrone
G Maccarrone
70INFN Laboratori Nazionali di Frascati, Frascati, Italy
70,
A Macchiolo
A Macchiolo
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
C M Macdonald
C M Macdonald
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
B Maček
B Maček
105Department of Physics, Jožef Stefan Institute, University of Ljubljana, Ljubljana, Slovenia
105,
J Machado Miguens
J Machado Miguens
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
160Faculdade de Ciências, Universidade de Lisboa, Lisbon, Portugal
154,160,
D Madaffari
D Madaffari
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
R Madar
R Madar
55Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
55,
H J Maddocks
H J Maddocks
217Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
217,
W F Mader
W F Mader
67Institut für Kern–und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
67,
A Madsen
A Madsen
65DESY, Hamburg and Zeuthen, Germany
65,
J Maeda
J Maeda
96Graduate School of Science, Kobe University, Kobe, Japan
96,
S Maeland
S Maeland
17Department for Physics and Technology, University of Bergen, Bergen, Norway
17,
T Maeno
T Maeno
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
A Maevskiy
A Maevskiy
129D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
129,
E Magradze
E Magradze
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
J Mahlstedt
J Mahlstedt
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
C Maiani
C Maiani
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
C Maidantchik
C Maidantchik
32Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
32,
A A Maier
A A Maier
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
T Maier
T Maier
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
A Maio
A Maio
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
160Faculdade de Ciências, Universidade de Lisboa, Lisbon, Portugal
162Centro de Física Nuclear da Universidade de Lisboa, Lisbon, Portugal
159,160,162,
S Majewski
S Majewski
147Center for High Energy Physics, University of Oregon, Eugene, OR USA
147,
Y Makida
Y Makida
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
N Makovec
N Makovec
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
B Malaescu
B Malaescu
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
Pa Malecki
Pa Malecki
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
V P Maleev
V P Maleev
155National Research Centre “Kurchatov Institute” B.P. Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
155,
F Malek
F Malek
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
U Mallik
U Mallik
92University of Iowa, Iowa City, IA USA
92,
D Malon
D Malon
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
C Malone
C Malone
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
S Maltezos
S Maltezos
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
S Malyukov
S Malyukov
45CERN, Geneva, Switzerland
45,
J Mamuzic
J Mamuzic
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
G Mancini
G Mancini
70INFN Laboratori Nazionali di Frascati, Frascati, Italy
70,
B Mandelli
B Mandelli
45CERN, Geneva, Switzerland
45,
L Mandelli
L Mandelli
121INFN Sezione di Milano, Milan, Italy
121,
I Mandić
I Mandić
105Department of Physics, Jožef Stefan Institute, University of Ljubljana, Ljubljana, Slovenia
105,
J Maneira
J Maneira
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
160Faculdade de Ciências, Universidade de Lisboa, Lisbon, Portugal
159,160,
L Manhaes de Andrade Filho
L Manhaes de Andrade Filho
33Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
33,
J Manjarres Ramos
J Manjarres Ramos
210Department of Physics and Astronomy, York University, Toronto, ON Canada
210,
A Mann
A Mann
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
A Manousos
A Manousos
45CERN, Geneva, Switzerland
45,
B Mansoulie
B Mansoulie
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
J D Mansour
J D Mansour
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
R Mantifel
R Mantifel
117Department of Physics, McGill University, Montreal, QC Canada
117,
M Mantoani
M Mantoani
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
S Manzoni
S Manzoni
121INFN Sezione di Milano, Milan, Italy
122Dipartimento di Fisica, Università di Milano, Milan, Italy
121,122,
L Mapelli
L Mapelli
45CERN, Geneva, Switzerland
45,
G Marceca
G Marceca
42Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
42,
L March
L March
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
G Marchiori
G Marchiori
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
M Marcisovsky
M Marcisovsky
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
M Marjanovic
M Marjanovic
16Institute of Physics, University of Belgrade, Belgrade, Serbia
16,
D E Marley
D E Marley
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
F Marroquim
F Marroquim
32Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
32,
S P Marsden
S P Marsden
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
Z Marshall
Z Marshall
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
S Marti-Garcia
S Marti-Garcia
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
B Martin
B Martin
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
T A Martin
T A Martin
222Department of Physics, University of Warwick, Coventry, UK
222,
V J Martin
V J Martin
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
B Martin dit Latour
B Martin dit Latour
17Department for Physics and Technology, University of Bergen, Bergen, Norway
17,
M Martinez
M Martinez
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
S Martin-Haugh
S Martin-Haugh
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
V S Martoiu
V S Martoiu
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
A C Martyniuk
A C Martyniuk
108Department of Physics and Astronomy, University College London, London, UK
108,
M Marx
M Marx
184Department of Physics, University of Washington, Seattle, WA USA
184,
A Marzin
A Marzin
45CERN, Geneva, Switzerland
45,
L Masetti
L Masetti
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
T Mashimo
T Mashimo
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
R Mashinistov
R Mashinistov
126P.N. Lebedev Physical Institute of the Russian, Academy of Sciences, Moscow, Russia
126,
J Masik
J Masik
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
A L Maslennikov
A L Maslennikov
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
I Massa
I Massa
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
L Massa
L Massa
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
P Mastrandrea
P Mastrandrea
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
A Mastroberardino
A Mastroberardino
58INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Cosenza, Italy
59Dipartimento di Fisica, Università della Calabria, Rende, Italy
58,59,
T Masubuchi
T Masubuchi
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
P Mättig
P Mättig
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
J Mattmann
J Mattmann
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
J Maurer
J Maurer
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
S J Maxfield
S J Maxfield
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
D A Maximov
D A Maximov
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
R Mazini
R Mazini
201Institute of Physics, Academia Sinica, Taipei, Taiwan
201,
S M Mazza
S M Mazza
121INFN Sezione di Milano, Milan, Italy
122Dipartimento di Fisica, Università di Milano, Milan, Italy
121,122,
N C Mc Fadden
N C Mc Fadden
136Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
136,
G Mc Goldrick
G Mc Goldrick
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
S P Mc Kee
S P Mc Kee
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
A McCarn
A McCarn
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
R L McCarthy
R L McCarthy
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
T G McCarthy
T G McCarthy
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
L I McClymont
L I McClymont
108Department of Physics and Astronomy, University College London, London, UK
108,
E F McDonald
E F McDonald
118School of Physics, University of Melbourne, Victoria, Australia
118,
K W McFarlane
K W McFarlane
1Department of Physics, University of Adelaide, Adelaide, Australia
81Department of Physics, Hampton University, Hampton, VA USA
1,81,
J A Mcfayden
J A Mcfayden
108Department of Physics and Astronomy, University College London, London, UK
108,
G Mchedlidze
G Mchedlidze
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
S J McMahon
S J McMahon
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
R A McPherson
R A McPherson
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
M Medinnis
M Medinnis
65DESY, Hamburg and Zeuthen, Germany
65,
S Meehan
S Meehan
184Department of Physics, University of Washington, Seattle, WA USA
184,
S Mehlhase
S Mehlhase
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
A Mehta
A Mehta
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
K Meier
K Meier
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
C Meineck
C Meineck
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
B Meirose
B Meirose
64Physics Department, University of Texas at Dallas, Richardson, TX USA
64,
D Melini
D Melini
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
B R Mellado Garcia
B R Mellado Garcia
194School of Physics, University of the Witwatersrand, Johannesburg, South Africa
194,
M Melo
M Melo
190Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
190,
F Meloni
F Meloni
20Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
20,
S B Menary
S B Menary
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
A Mengarelli
A Mengarelli
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
S Menke
S Menke
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
E Meoni
E Meoni
212Department of Physics and Astronomy, Tufts University, Medford, MA United States of America
212,
S Mergelmeyer
S Mergelmeyer
19Department of Physics, Humboldt University, Berlin, Germany
19,
P Mermod
P Mermod
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
L Merola
L Merola
134INFN Sezione di Napoli, Naples, Italy
135Dipartimento di Fisica, Università di Napoli, Naples, Italy
134,135,
C Meroni
C Meroni
121INFN Sezione di Milano, Milan, Italy
121,
F S Merritt
F S Merritt
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
A Messina
A Messina
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
J Metcalfe
J Metcalfe
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
A S Mete
A S Mete
213Department of Physics and Astronomy, University of California Irvine, Irvine, CA USA
213,
C Meyer
C Meyer
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
C Meyer
C Meyer
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
J-P Meyer
J-P Meyer
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
J Meyer
J Meyer
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
H Meyer Zu Theenhausen
H Meyer Zu Theenhausen
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
F Miano
F Miano
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
R P Middleton
R P Middleton
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
S Miglioranzi
S Miglioranzi
73INFN Sezione di Genova, Genoa, Italy
74Dipartimento di Fisica, Università di Genova, Genoa, Italy
73,74,
L Mijović
L Mijović
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
G Mikenberg
G Mikenberg
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
M Mikestikova
M Mikestikova
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
M Mikuž
M Mikuž
105Department of Physics, Jožef Stefan Institute, University of Ljubljana, Ljubljana, Slovenia
105,
M Milesi
M Milesi
118School of Physics, University of Melbourne, Victoria, Australia
118,
A Milic
A Milic
91Institut für Astro–und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
91,
D W Miller
D W Miller
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
C Mills
C Mills
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
A Milov
A Milov
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
D A Milstead
D A Milstead
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
A A Minaenko
A A Minaenko
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
Y Minami
Y Minami
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
I A Minashvili
I A Minashvili
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
A I Mincer
A I Mincer
141Department of Physics, New York University, New York, NY USA
141,
B Mindur
B Mindur
60AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Kraków, Poland
60,
M Mineev
M Mineev
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
Y Ming
Y Ming
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
L M Mir
L M Mir
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
K P Mistry
K P Mistry
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
T Mitani
T Mitani
223Waseda University, Tokyo, Japan
223,
J Mitrevski
J Mitrevski
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
V A Mitsou
V A Mitsou
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
A Miucci
A Miucci
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
P S Miyagawa
P S Miyagawa
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
J U Mjörnmark
J U Mjörnmark
111Fysiska institutionen, Lunds universitet, Lund, Sweden
111,
T Moa
T Moa
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
K Mochizuki
K Mochizuki
125Group of Particle Physics, University of Montreal, Montreal, QC Canada
125,
S Mohapatra
S Mohapatra
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
S Molander
S Molander
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
R Moles-Valls
R Moles-Valls
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
R Monden
R Monden
97Faculty of Science, Kyoto University, Kyoto, Japan
97,
M C Mondragon
M C Mondragon
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
K Mönig
K Mönig
65DESY, Hamburg and Zeuthen, Germany
65,
J Monk
J Monk
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
E Monnier
E Monnier
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
A Montalbano
A Montalbano
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
J Montejo Berlingen
J Montejo Berlingen
45CERN, Geneva, Switzerland
45,
F Monticelli
F Monticelli
100Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
100,
S Monzani
S Monzani
121INFN Sezione di Milano, Milan, Italy
122Dipartimento di Fisica, Università di Milano, Milan, Italy
121,122,
R W Moore
R W Moore
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
N Morange
N Morange
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
D Moreno
D Moreno
26Centro de Investigaciones, Universidad Antonio Narino, Bogotá, Colombia
26,
M Moreno Llácer
M Moreno Llácer
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
P Morettini
P Morettini
73INFN Sezione di Genova, Genoa, Italy
73,
D Mori
D Mori
188Department of Physics, Simon Fraser University, Burnaby, BC Canada
188,
T Mori
T Mori
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
M Morii
M Morii
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
M Morinaga
M Morinaga
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
V Morisbak
V Morisbak
150Department of Physics, University of Oslo, Oslo, Norway
150,
S Moritz
S Moritz
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
A K Morley
A K Morley
200School of Physics, University of Sydney, Sydney, Australia
200,
G Mornacchi
G Mornacchi
45CERN, Geneva, Switzerland
45,
J D Morris
J D Morris
106School of Physics and Astronomy, Queen Mary University of London, London, UK
106,
S S Mortensen
S S Mortensen
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
L Morvaj
L Morvaj
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
M Mosidze
M Mosidze
76High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
76,
J Moss
J Moss
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
K Motohashi
K Motohashi
207Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
207,
R Mount
R Mount
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
E Mountricha
E Mountricha
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
S V Mouraviev
S V Mouraviev
1Department of Physics, University of Adelaide, Adelaide, Australia
126P.N. Lebedev Physical Institute of the Russian, Academy of Sciences, Moscow, Russia
1,126,
E J W Moyse
E J W Moyse
116Department of Physics, University of Massachusetts, Amherst, MA USA
116,
S Muanza
S Muanza
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
R D Mudd
R D Mudd
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
F Mueller
F Mueller
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
J Mueller
J Mueller
158Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
158,
R S P Mueller
R S P Mueller
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
T Mueller
T Mueller
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
D Muenstermann
D Muenstermann
101Physics Department, Lancaster University, Lancaster, UK
101,
P Mullen
P Mullen
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
G A Mullier
G A Mullier
20Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
20,
F J Munoz Sanchez
F J Munoz Sanchez
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
J A Murillo Quijada
J A Murillo Quijada
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
W J Murray
W J Murray
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
222Department of Physics, University of Warwick, Coventry, UK
170,222,
H Musheghyan
H Musheghyan
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
M Muškinja
M Muškinja
105Department of Physics, Jožef Stefan Institute, University of Ljubljana, Ljubljana, Slovenia
105,
A G Myagkov
A G Myagkov
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
M Myska
M Myska
167Czech Technical University in Prague, Prague, Czech Republic
167,
B P Nachman
B P Nachman
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
O Nackenhorst
O Nackenhorst
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
K Nagai
K Nagai
151Department of Physics, Oxford University, Oxford, UK
151,
R Nagai
R Nagai
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
K Nagano
K Nagano
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
Y Nagasaka
Y Nagasaka
86Faculty of Applied Information Science, Hiroshima Institute of Technology, Hiroshima, Japan
86,
K Nagata
K Nagata
211Faculty of Pure and Applied Sciences, and Center for Integrated Research in Fundamental Science and Engineering, University of Tsukuba, Tsukuba, Japan
211,
M Nagel
M Nagel
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
E Nagy
E Nagy
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
A M Nairz
A M Nairz
45CERN, Geneva, Switzerland
45,
Y Nakahama
Y Nakahama
45CERN, Geneva, Switzerland
45,
K Nakamura
K Nakamura
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
T Nakamura
T Nakamura
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
I Nakano
I Nakano
143Faculty of Science, Okayama University, Okayama, Japan
143,
H Namasivayam
H Namasivayam
64Physics Department, University of Texas at Dallas, Richardson, TX USA
64,
R F Naranjo Garcia
R F Naranjo Garcia
65DESY, Hamburg and Zeuthen, Germany
65,
R Narayan
R Narayan
13Department of Physics, The University of Texas at Austin, Austin, TX USA
13,
D I Narrias Villar
D I Narrias Villar
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
I Naryshkin
I Naryshkin
155National Research Centre “Kurchatov Institute” B.P. Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
155,
T Naumann
T Naumann
65DESY, Hamburg and Zeuthen, Germany
65,
G Navarro
G Navarro
26Centro de Investigaciones, Universidad Antonio Narino, Bogotá, Colombia
26,
R Nayyar
R Nayyar
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
H A Neal
H A Neal
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
P Yu Nechaeva
P Yu Nechaeva
126P.N. Lebedev Physical Institute of the Russian, Academy of Sciences, Moscow, Russia
126,
T J Neep
T J Neep
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
P D Nef
P D Nef
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
A Negri
A Negri
152INFN Sezione di Pavia, Pavia, Italy
153Dipartimento di Fisica, Università di Pavia, Pavia, Italy
152,153,
M Negrini
M Negrini
27INFN Sezione di Bologna, Bologna, Italy
27,
S Nektarijevic
S Nektarijevic
137Institute for Mathematics Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
137,
C Nellist
C Nellist
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
A Nelson
A Nelson
213Department of Physics and Astronomy, University of California Irvine, Irvine, CA USA
213,
S Nemecek
S Nemecek
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
P Nemethy
P Nemethy
141Department of Physics, New York University, New York, NY USA
141,
A A Nepomuceno
A A Nepomuceno
32Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
32,
M Nessi
M Nessi
45CERN, Geneva, Switzerland
45,
M S Neubauer
M S Neubauer
218Department of Physics, University of Illinois, Urbana, IL USA
218,
M Neumann
M Neumann
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
R M Neves
R M Neves
141Department of Physics, New York University, New York, NY USA
141,
P Nevski
P Nevski
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
P R Newman
P R Newman
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
D H Nguyen
D H Nguyen
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
T Nguyen Manh
T Nguyen Manh
125Group of Particle Physics, University of Montreal, Montreal, QC Canada
125,
R B Nickerson
R B Nickerson
151Department of Physics, Oxford University, Oxford, UK
151,
R Nicolaidou
R Nicolaidou
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
J Nielsen
J Nielsen
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
A Nikiforov
A Nikiforov
19Department of Physics, Humboldt University, Berlin, Germany
19,
V Nikolaenko
V Nikolaenko
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
I Nikolic-Audit
I Nikolic-Audit
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
K Nikolopoulos
K Nikolopoulos
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
J K Nilsen
J K Nilsen
150Department of Physics, University of Oslo, Oslo, Norway
150,
P Nilsson
P Nilsson
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
Y Ninomiya
Y Ninomiya
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
A Nisati
A Nisati
171INFN Sezione di Roma, Rome, Italy
171,
R Nisius
R Nisius
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
T Nobe
T Nobe
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
L Nodulman
L Nodulman
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
M Nomachi
M Nomachi
149Graduate School of Science, Osaka University, Osaka, Japan
149,
I Nomidis
I Nomidis
44Department of Physics, Carleton University, Ottawa, ON Canada
44,
T Nooney
T Nooney
106School of Physics and Astronomy, Queen Mary University of London, London, UK
106,
S Norberg
S Norberg
144Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
144,
M Nordberg
M Nordberg
45CERN, Geneva, Switzerland
45,
N Norjoharuddeen
N Norjoharuddeen
151Department of Physics, Oxford University, Oxford, UK
151,
O Novgorodova
O Novgorodova
67Institut für Kern–und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
67,
S Nowak
S Nowak
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
M Nozaki
M Nozaki
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
L Nozka
L Nozka
146Palacký University, RCPTM, Olomouc, Czech Republic
146,
K Ntekas
K Ntekas
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
E Nurse
E Nurse
108Department of Physics and Astronomy, University College London, London, UK
108,
F Nuti
F Nuti
118School of Physics, University of Melbourne, Victoria, Australia
118,
F O’grady
F O’grady
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
D C O’Neil
D C O’Neil
188Department of Physics, Simon Fraser University, Burnaby, BC Canada
188,
A A O’Rourke
A A O’Rourke
65DESY, Hamburg and Zeuthen, Germany
65,
V O’Shea
V O’Shea
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
F G Oakham
F G Oakham
44Department of Physics, Carleton University, Ottawa, ON Canada
44,
H Oberlack
H Oberlack
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
T Obermann
T Obermann
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
J Ocariz
J Ocariz
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
A Ochi
A Ochi
96Graduate School of Science, Kobe University, Kobe, Japan
96,
I Ochoa
I Ochoa
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
J P Ochoa-Ricoux
J P Ochoa-Ricoux
47Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
47,
S Oda
S Oda
99Department of Physics, Kyushu University, Fukuoka, Japan
99,
S Odaka
S Odaka
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
H Ogren
H Ogren
90Department of Physics, Indiana University, Bloomington, IN USA
90,
A Oh
A Oh
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
S H Oh
S H Oh
68Department of Physics, Duke University, Durham, NC USA
68,
C C Ohm
C C Ohm
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
H Ohman
H Ohman
217Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
217,
H Oide
H Oide
45CERN, Geneva, Switzerland
45,
H Okawa
H Okawa
211Faculty of Pure and Applied Sciences, and Center for Integrated Research in Fundamental Science and Engineering, University of Tsukuba, Tsukuba, Japan
211,
Y Okumura
Y Okumura
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
T Okuyama
T Okuyama
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
A Olariu
A Olariu
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
L F Oleiro Seabra
L F Oleiro Seabra
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
159,
S A Olivares Pino
S A Olivares Pino
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
D Oliveira Damazio
D Oliveira Damazio
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
A Olszewski
A Olszewski
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
J Olszowska
J Olszowska
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
A Onofre
A Onofre
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
163Departamento de Fisica, Universidade do Minho, Braga, Portugal
159,163,
K Onogi
K Onogi
133Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
133,
P U E Onyisi
P U E Onyisi
13Department of Physics, The University of Texas at Austin, Austin, TX USA
13,
M J Oreglia
M J Oreglia
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
Y Oren
Y Oren
203Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
203,
D Orestano
D Orestano
175INFN Sezione di Roma Tre, Rome, Italy
176Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
175,176,
N Orlando
N Orlando
88Department of Physics, The University of Hong Kong, Pokfulam, Hong Kong
88,
R S Orr
R S Orr
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
B Osculati
B Osculati
73INFN Sezione di Genova, Genoa, Italy
74Dipartimento di Fisica, Università di Genova, Genoa, Italy
73,74,
R Ospanov
R Ospanov
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
G Otero y Garzon
G Otero y Garzon
42Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
42,
H Otono
H Otono
99Department of Physics, Kyushu University, Fukuoka, Japan
99,
M Ouchrif
M Ouchrif
180Faculté des Sciences, Université Mohamed Premier and LPTPM, Oujda, Morocco
180,
F Ould-Saada
F Ould-Saada
150Department of Physics, University of Oslo, Oslo, Norway
150,
A Ouraou
A Ouraou
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
K P Oussoren
K P Oussoren
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
Q Ouyang
Q Ouyang
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
M Owen
M Owen
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
R E Owen
R E Owen
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
V E Ozcan
V E Ozcan
22Department of Physics, Bogazici University, Istanbul, Turkey
22,
N Ozturk
N Ozturk
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
K Pachal
K Pachal
188Department of Physics, Simon Fraser University, Burnaby, BC Canada
188,
A Pacheco Pages
A Pacheco Pages
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
C Padilla Aranda
C Padilla Aranda
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
M Pagáčová
M Pagáčová
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
S Pagan Griso
S Pagan Griso
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
F Paige
F Paige
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
P Pais
P Pais
116Department of Physics, University of Massachusetts, Amherst, MA USA
116,
K Pajchel
K Pajchel
150Department of Physics, University of Oslo, Oslo, Norway
150,
G Palacino
G Palacino
210Department of Physics and Astronomy, York University, Toronto, ON Canada
210,
S Palestini
S Palestini
45CERN, Geneva, Switzerland
45,
M Palka
M Palka
61Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
61,
D Pallin
D Pallin
55Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
55,
A Palma
A Palma
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
160Faculdade de Ciências, Universidade de Lisboa, Lisbon, Portugal
159,160,
E St Panagiotopoulou
E St Panagiotopoulou
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
C E Pandini
C E Pandini
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
J G Panduro Vazquez
J G Panduro Vazquez
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
P Pani
P Pani
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
S Panitkin
S Panitkin
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
D Pantea
D Pantea
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
L Paolozzi
L Paolozzi
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
Th D Papadopoulou
Th D Papadopoulou
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
K Papageorgiou
K Papageorgiou
204Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
204,
A Paramonov
A Paramonov
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
D Paredes Hernandez
D Paredes Hernandez
228Department of Physics, Yale University, New Haven, CT USA
228,
A J Parker
A J Parker
101Physics Department, Lancaster University, Lancaster, UK
101,
M A Parker
M A Parker
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
K A Parker
K A Parker
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
F Parodi
F Parodi
73INFN Sezione di Genova, Genoa, Italy
74Dipartimento di Fisica, Università di Genova, Genoa, Italy
73,74,
J A Parsons
J A Parsons
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
U Parzefall
U Parzefall
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
V R Pascuzzi
V R Pascuzzi
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
E Pasqualucci
E Pasqualucci
171INFN Sezione di Roma, Rome, Italy
171,
S Passaggio
S Passaggio
73INFN Sezione di Genova, Genoa, Italy
73,
Fr Pastore
Fr Pastore
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
G Pásztor
G Pásztor
44Department of Physics, Carleton University, Ottawa, ON Canada
44,
S Pataraia
S Pataraia
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
J R Pater
J R Pater
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
T Pauly
T Pauly
45CERN, Geneva, Switzerland
45,
J Pearce
J Pearce
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
B Pearson
B Pearson
144Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
144,
L E Pedersen
L E Pedersen
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
M Pedersen
M Pedersen
150Department of Physics, University of Oslo, Oslo, Norway
150,
S Pedraza Lopez
S Pedraza Lopez
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
R Pedro
R Pedro
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
160Faculdade de Ciências, Universidade de Lisboa, Lisbon, Portugal
159,160,
S V Peleganchuk
S V Peleganchuk
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
D Pelikan
D Pelikan
217Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
217,
O Penc
O Penc
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
C Peng
C Peng
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
H Peng
H Peng
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
J Penwell
J Penwell
90Department of Physics, Indiana University, Bloomington, IN USA
90,
B S Peralva
B S Peralva
33Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
33,
M M Perego
M M Perego
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
D V Perepelitsa
D V Perepelitsa
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
E Perez Codina
E Perez Codina
209TRIUMF, Vancouver, BC Canada
209,
L Perini
L Perini
121INFN Sezione di Milano, Milan, Italy
122Dipartimento di Fisica, Università di Milano, Milan, Italy
121,122,
H Pernegger
H Pernegger
45CERN, Geneva, Switzerland
45,
S Perrella
S Perrella
134INFN Sezione di Napoli, Naples, Italy
135Dipartimento di Fisica, Università di Napoli, Naples, Italy
134,135,
R Peschke
R Peschke
65DESY, Hamburg and Zeuthen, Germany
65,
V D Peshekhonov
V D Peshekhonov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
K Peters
K Peters
65DESY, Hamburg and Zeuthen, Germany
65,
R F Y Peters
R F Y Peters
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
B A Petersen
B A Petersen
45CERN, Geneva, Switzerland
45,
T C Petersen
T C Petersen
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
E Petit
E Petit
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
A Petridis
A Petridis
1Department of Physics, University of Adelaide, Adelaide, Australia
1,
C Petridou
C Petridou
204Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
204,
P Petroff
P Petroff
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
E Petrolo
E Petrolo
171INFN Sezione di Roma, Rome, Italy
171,
M Petrov
M Petrov
151Department of Physics, Oxford University, Oxford, UK
151,
F Petrucci
F Petrucci
175INFN Sezione di Roma Tre, Rome, Italy
176Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
175,176,
N E Pettersson
N E Pettersson
116Department of Physics, University of Massachusetts, Amherst, MA USA
116,
A Peyaud
A Peyaud
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
R Pezoa
R Pezoa
48Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
48,
P W Phillips
P W Phillips
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
G Piacquadio
G Piacquadio
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
E Pianori
E Pianori
222Department of Physics, University of Warwick, Coventry, UK
222,
A Picazio
A Picazio
116Department of Physics, University of Massachusetts, Amherst, MA USA
116,
E Piccaro
E Piccaro
106School of Physics and Astronomy, Queen Mary University of London, London, UK
106,
M Piccinini
M Piccinini
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
M A Pickering
M A Pickering
151Department of Physics, Oxford University, Oxford, UK
151,
R Piegaia
R Piegaia
42Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
42,
J E Pilcher
J E Pilcher
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
A D Pilkington
A D Pilkington
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
A W J Pin
A W J Pin
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
M Pinamonti
M Pinamonti
164Departamento de Fisica Teorica y del Cosmos and CAFPE, Universidad de Granada, Granada, Spain
164,
J L Pinfold
J L Pinfold
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
A Pingel
A Pingel
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
S Pires
S Pires
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
H Pirumov
H Pirumov
65DESY, Hamburg and Zeuthen, Germany
65,
M Pitt
M Pitt
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
L Plazak
L Plazak
190Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
190,
M-A Pleier
M-A Pleier
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
V Pleskot
V Pleskot
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
E Plotnikova
E Plotnikova
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
P Plucinski
P Plucinski
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
D Pluth
D Pluth
93Department of Physics and Astronomy, Iowa State University, Ames, IA USA
93,
R Poettgen
R Poettgen
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
L Poggioli
L Poggioli
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
D Pohl
D Pohl
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
G Polesello
G Polesello
152INFN Sezione di Pavia, Pavia, Italy
152,
A Poley
A Poley
65DESY, Hamburg and Zeuthen, Germany
65,
A Policicchio
A Policicchio
58INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Cosenza, Italy
59Dipartimento di Fisica, Università della Calabria, Rende, Italy
58,59,
R Polifka
R Polifka
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
A Polini
A Polini
27INFN Sezione di Bologna, Bologna, Italy
27,
C S Pollard
C S Pollard
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
V Polychronakos
V Polychronakos
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
K Pommès
K Pommès
45CERN, Geneva, Switzerland
45,
L Pontecorvo
L Pontecorvo
171INFN Sezione di Roma, Rome, Italy
171,
B G Pope
B G Pope
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
G A Popeneciu
G A Popeneciu
39Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj-Napoca, Romania
39,
D S Popovic
D S Popovic
16Institute of Physics, University of Belgrade, Belgrade, Serbia
16,
A Poppleton
A Poppleton
45CERN, Geneva, Switzerland
45,
S Pospisil
S Pospisil
167Czech Technical University in Prague, Prague, Czech Republic
167,
K Potamianos
K Potamianos
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
I N Potrap
I N Potrap
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
C J Potter
C J Potter
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
C T Potter
C T Potter
147Center for High Energy Physics, University of Oregon, Eugene, OR USA
147,
G Poulard
G Poulard
45CERN, Geneva, Switzerland
45,
J Poveda
J Poveda
45CERN, Geneva, Switzerland
45,
V Pozdnyakov
V Pozdnyakov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
M E Pozo Astigarraga
M E Pozo Astigarraga
45CERN, Geneva, Switzerland
45,
P Pralavorio
P Pralavorio
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
A Pranko
A Pranko
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
S Prell
S Prell
93Department of Physics and Astronomy, Iowa State University, Ames, IA USA
93,
D Price
D Price
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
L E Price
L E Price
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
M Primavera
M Primavera
102INFN Sezione di Lecce, Lecce, Italy
102,
S Prince
S Prince
117Department of Physics, McGill University, Montreal, QC Canada
117,
M Proissl
M Proissl
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
K Prokofiev
K Prokofiev
89Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
89,
F Prokoshin
F Prokoshin
48Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
48,
S Protopopescu
S Protopopescu
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
J Proudfoot
J Proudfoot
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
M Przybycien
M Przybycien
60AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Kraków, Poland
60,
D Puddu
D Puddu
175INFN Sezione di Roma Tre, Rome, Italy
176Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
175,176,
M Purohit
M Purohit
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
P Puzo
P Puzo
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
J Qian
J Qian
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
G Qin
G Qin
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
Y Qin
Y Qin
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
A Quadt
A Quadt
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
W B Quayle
W B Quayle
214INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
215ICTP, Trieste, Italy
214,215,
M Queitsch-Maitland
M Queitsch-Maitland
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
D Quilty
D Quilty
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
S Raddum
S Raddum
150Department of Physics, University of Oslo, Oslo, Norway
150,
V Radeka
V Radeka
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
V Radescu
V Radescu
84Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
84,
S K Radhakrishnan
S K Radhakrishnan
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
P Radloff
P Radloff
147Center for High Energy Physics, University of Oregon, Eugene, OR USA
147,
P Rados
P Rados
118School of Physics, University of Melbourne, Victoria, Australia
118,
F Ragusa
F Ragusa
121INFN Sezione di Milano, Milan, Italy
122Dipartimento di Fisica, Università di Milano, Milan, Italy
121,122,
G Rahal
G Rahal
230Centre de Calcul de l’Institut National de Physique Nucléaire et de Physique des Particules (IN2P3), Villeurbanne, France
230,
J A Raine
J A Raine
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
S Rajagopalan
S Rajagopalan
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
M Rammensee
M Rammensee
45CERN, Geneva, Switzerland
45,
C Rangel-Smith
C Rangel-Smith
217Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
217,
M G Ratti
M G Ratti
121INFN Sezione di Milano, Milan, Italy
122Dipartimento di Fisica, Università di Milano, Milan, Italy
121,122,
F Rauscher
F Rauscher
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
S Rave
S Rave
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
T Ravenscroft
T Ravenscroft
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
I Ravinovich
I Ravinovich
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
M Raymond
M Raymond
45CERN, Geneva, Switzerland
45,
A L Read
A L Read
150Department of Physics, University of Oslo, Oslo, Norway
150,
N P Readioff
N P Readioff
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
M Reale
M Reale
102INFN Sezione di Lecce, Lecce, Italy
103Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
102,103,
D M Rebuzzi
D M Rebuzzi
152INFN Sezione di Pavia, Pavia, Italy
153Dipartimento di Fisica, Università di Pavia, Pavia, Italy
152,153,
A Redelbach
A Redelbach
226Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
226,
G Redlinger
G Redlinger
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
R Reece
R Reece
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
K Reeves
K Reeves
64Physics Department, University of Texas at Dallas, Richardson, TX USA
64,
L Rehnisch
L Rehnisch
19Department of Physics, Humboldt University, Berlin, Germany
19,
J Reichert
J Reichert
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
H Reisin
H Reisin
42Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
42,
C Rembser
C Rembser
45CERN, Geneva, Switzerland
45,
H Ren
H Ren
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
M Rescigno
M Rescigno
171INFN Sezione di Roma, Rome, Italy
171,
S Resconi
S Resconi
121INFN Sezione di Milano, Milan, Italy
121,
O L Rezanova
O L Rezanova
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
P Reznicek
P Reznicek
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
R Rezvani
R Rezvani
125Group of Particle Physics, University of Montreal, Montreal, QC Canada
125,
R Richter
R Richter
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
S Richter
S Richter
108Department of Physics and Astronomy, University College London, London, UK
108,
E Richter-Was
E Richter-Was
61Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
61,
O Ricken
O Ricken
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
M Ridel
M Ridel
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
P Rieck
P Rieck
19Department of Physics, Humboldt University, Berlin, Germany
19,
C J Riegel
C J Riegel
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
J Rieger
J Rieger
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
O Rifki
O Rifki
144Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
144,
M Rijssenbeek
M Rijssenbeek
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
A Rimoldi
A Rimoldi
152INFN Sezione di Pavia, Pavia, Italy
153Dipartimento di Fisica, Università di Pavia, Pavia, Italy
152,153,
M Rimoldi
M Rimoldi
20Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
20,
L Rinaldi
L Rinaldi
27INFN Sezione di Bologna, Bologna, Italy
27,
B Ristić
B Ristić
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
E Ritsch
E Ritsch
45CERN, Geneva, Switzerland
45,
I Riu
I Riu
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
F Rizatdinova
F Rizatdinova
145Department of Physics, Oklahoma State University, Stillwater, OK USA
145,
E Rizvi
E Rizvi
106School of Physics and Astronomy, Queen Mary University of London, London, UK
106,
C Rizzi
C Rizzi
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
S H Robertson
S H Robertson
117Department of Physics, McGill University, Montreal, QC Canada
117,
A Robichaud-Veronneau
A Robichaud-Veronneau
117Department of Physics, McGill University, Montreal, QC Canada
117,
D Robinson
D Robinson
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
J E M Robinson
J E M Robinson
65DESY, Hamburg and Zeuthen, Germany
65,
A Robson
A Robson
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
C Roda
C Roda
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
Y Rodina
Y Rodina
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
A Rodriguez Perez
A Rodriguez Perez
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
D Rodriguez Rodriguez
D Rodriguez Rodriguez
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
S Roe
S Roe
45CERN, Geneva, Switzerland
45,
C S Rogan
C S Rogan
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
O Røhne
O Røhne
150Department of Physics, University of Oslo, Oslo, Norway
150,
A Romaniouk
A Romaniouk
128National Research Nuclear University MEPhI, Moscow, Russia
128,
M Romano
M Romano
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
S M Romano Saez
S M Romano Saez
55Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
55,
E Romero Adam
E Romero Adam
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
N Rompotis
N Rompotis
184Department of Physics, University of Washington, Seattle, WA USA
184,
M Ronzani
M Ronzani
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
L Roos
L Roos
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
E Ros
E Ros
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
S Rosati
S Rosati
171INFN Sezione di Roma, Rome, Italy
171,
K Rosbach
K Rosbach
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
P Rose
P Rose
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
O Rosenthal
O Rosenthal
187Fachbereich Physik, Universität Siegen, Siegen, Germany
187,
N -A Rosien
N -A Rosien
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
V Rossetti
V Rossetti
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
E Rossi
E Rossi
134INFN Sezione di Napoli, Naples, Italy
135Dipartimento di Fisica, Università di Napoli, Naples, Italy
134,135,
L P Rossi
L P Rossi
73INFN Sezione di Genova, Genoa, Italy
73,
J H N Rosten
J H N Rosten
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
R Rosten
R Rosten
184Department of Physics, University of Washington, Seattle, WA USA
184,
M Rotaru
M Rotaru
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
I Roth
I Roth
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
J Rothberg
J Rothberg
184Department of Physics, University of Washington, Seattle, WA USA
184,
D Rousseau
D Rousseau
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
C R Royon
C R Royon
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
A Rozanov
A Rozanov
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
Y Rozen
Y Rozen
202Department of Physics, Technion: Israel Institute of Technology, Haifa, Israel
202,
X Ruan
X Ruan
194School of Physics, University of the Witwatersrand, Johannesburg, South Africa
194,
F Rubbo
F Rubbo
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
M S Rudolph
M S Rudolph
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
F Rühr
F Rühr
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
A Ruiz-Martinez
A Ruiz-Martinez
44Department of Physics, Carleton University, Ottawa, ON Canada
44,
Z Rurikova
Z Rurikova
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
N A Rusakovich
N A Rusakovich
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
A Ruschke
A Ruschke
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
H L Russell
H L Russell
184Department of Physics, University of Washington, Seattle, WA USA
184,
J P Rutherfoord
J P Rutherfoord
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
N Ruthmann
N Ruthmann
45CERN, Geneva, Switzerland
45,
Y F Ryabov
Y F Ryabov
155National Research Centre “Kurchatov Institute” B.P. Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
155,
M Rybar
M Rybar
218Department of Physics, University of Illinois, Urbana, IL USA
218,
G Rybkin
G Rybkin
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
S Ryu
S Ryu
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
A Ryzhov
A Ryzhov
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
G F Rzehorz
G F Rzehorz
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
A F Saavedra
A F Saavedra
200School of Physics, University of Sydney, Sydney, Australia
200,
G Sabato
G Sabato
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
S Sacerdoti
S Sacerdoti
42Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
42,
H F-W Sadrozinski
H F-W Sadrozinski
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
R Sadykov
R Sadykov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
F Safai Tehrani
F Safai Tehrani
171INFN Sezione di Roma, Rome, Italy
171,
P Saha
P Saha
139Department of Physics, Northern Illinois University, DeKalb, IL USA
139,
M Sahinsoy
M Sahinsoy
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
M Saimpert
M Saimpert
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
T Saito
T Saito
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
H Sakamoto
H Sakamoto
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
Y Sakurai
Y Sakurai
223Waseda University, Tokyo, Japan
223,
G Salamanna
G Salamanna
175INFN Sezione di Roma Tre, Rome, Italy
176Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
175,176,
A Salamon
A Salamon
173INFN Sezione di Roma Tor Vergata, Rome, Italy
174Dipartimento di Fisica, Università di Roma Tor Vergata, Rome, Italy
173,174,
J E Salazar Loyola
J E Salazar Loyola
48Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
48,
D Salek
D Salek
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
P H Sales De Bruin
P H Sales De Bruin
184Department of Physics, University of Washington, Seattle, WA USA
184,
D Salihagic
D Salihagic
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
A Salnikov
A Salnikov
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
J Salt
J Salt
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
D Salvatore
D Salvatore
58INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Cosenza, Italy
59Dipartimento di Fisica, Università della Calabria, Rende, Italy
58,59,
F Salvatore
F Salvatore
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
A Salvucci
A Salvucci
87Department of Physics, The Chinese University of Hong Kong, Shatin, NT Hong Kong
87,
A Salzburger
A Salzburger
45CERN, Geneva, Switzerland
45,
D Sammel
D Sammel
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
D Sampsonidis
D Sampsonidis
204Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
204,
A Sanchez
A Sanchez
134INFN Sezione di Napoli, Naples, Italy
135Dipartimento di Fisica, Università di Napoli, Naples, Italy
134,135,
J Sánchez
J Sánchez
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
V Sanchez Martinez
V Sanchez Martinez
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
H Sandaker
H Sandaker
150Department of Physics, University of Oslo, Oslo, Norway
150,
R L Sandbach
R L Sandbach
106School of Physics and Astronomy, Queen Mary University of London, London, UK
106,
H G Sander
H G Sander
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
M Sandhoff
M Sandhoff
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
C Sandoval
C Sandoval
26Centro de Investigaciones, Universidad Antonio Narino, Bogotá, Colombia
26,
R Sandstroem
R Sandstroem
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
D P C Sankey
D P C Sankey
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
M Sannino
M Sannino
73INFN Sezione di Genova, Genoa, Italy
74Dipartimento di Fisica, Università di Genova, Genoa, Italy
73,74,
A Sansoni
A Sansoni
70INFN Laboratori Nazionali di Frascati, Frascati, Italy
70,
C Santoni
C Santoni
55Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
55,
R Santonico
R Santonico
173INFN Sezione di Roma Tor Vergata, Rome, Italy
174Dipartimento di Fisica, Università di Roma Tor Vergata, Rome, Italy
173,174,
H Santos
H Santos
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
159,
I Santoyo Castillo
I Santoyo Castillo
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
K Sapp
K Sapp
158Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
158,
A Sapronov
A Sapronov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
J G Saraiva
J G Saraiva
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
162Centro de Física Nuclear da Universidade de Lisboa, Lisbon, Portugal
159,162,
B Sarrazin
B Sarrazin
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
O Sasaki
O Sasaki
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
Y Sasaki
Y Sasaki
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
K Sato
K Sato
211Faculty of Pure and Applied Sciences, and Center for Integrated Research in Fundamental Science and Engineering, University of Tsukuba, Tsukuba, Japan
211,
G Sauvage
G Sauvage
1Department of Physics, University of Adelaide, Adelaide, Australia
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
1,7,
E Sauvan
E Sauvan
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
G Savage
G Savage
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
P Savard
P Savard
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
C Sawyer
C Sawyer
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
L Sawyer
L Sawyer
109Louisiana Tech University, Ruston, LA USA
109,
J Saxon
J Saxon
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
C Sbarra
C Sbarra
27INFN Sezione di Bologna, Bologna, Italy
27,
A Sbrizzi
A Sbrizzi
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
T Scanlon
T Scanlon
108Department of Physics and Astronomy, University College London, London, UK
108,
D A Scannicchio
D A Scannicchio
213Department of Physics and Astronomy, University of California Irvine, Irvine, CA USA
213,
M Scarcella
M Scarcella
200School of Physics, University of Sydney, Sydney, Australia
200,
V Scarfone
V Scarfone
58INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Cosenza, Italy
59Dipartimento di Fisica, Università della Calabria, Rende, Italy
58,59,
J Schaarschmidt
J Schaarschmidt
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
P Schacht
P Schacht
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
B M Schachtner
B M Schachtner
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
D Schaefer
D Schaefer
45CERN, Geneva, Switzerland
45,
R Schaefer
R Schaefer
65DESY, Hamburg and Zeuthen, Germany
65,
J Schaeffer
J Schaeffer
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
S Schaepe
S Schaepe
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
S Schaetzel
S Schaetzel
84Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
84,
U Schäfer
U Schäfer
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
A C Schaffer
A C Schaffer
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
D Schaile
D Schaile
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
R D Schamberger
R D Schamberger
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
V Scharf
V Scharf
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
V A Schegelsky
V A Schegelsky
155National Research Centre “Kurchatov Institute” B.P. Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
155,
D Scheirich
D Scheirich
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
M Schernau
M Schernau
213Department of Physics and Astronomy, University of California Irvine, Irvine, CA USA
213,
C Schiavi
C Schiavi
73INFN Sezione di Genova, Genoa, Italy
74Dipartimento di Fisica, Università di Genova, Genoa, Italy
73,74,
S Schier
S Schier
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
C Schillo
C Schillo
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
M Schioppa
M Schioppa
58INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Cosenza, Italy
59Dipartimento di Fisica, Università della Calabria, Rende, Italy
58,59,
S Schlenker
S Schlenker
45CERN, Geneva, Switzerland
45,
K R Schmidt-Sommerfeld
K R Schmidt-Sommerfeld
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
K Schmieden
K Schmieden
45CERN, Geneva, Switzerland
45,
C Schmitt
C Schmitt
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
S Schmitt
S Schmitt
65DESY, Hamburg and Zeuthen, Germany
65,
S Schmitz
S Schmitz
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
B Schneider
B Schneider
209TRIUMF, Vancouver, BC Canada
209,
U Schnoor
U Schnoor
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
L Schoeffel
L Schoeffel
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
A Schoening
A Schoening
84Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
84,
B D Schoenrock
B D Schoenrock
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
E Schopf
E Schopf
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
M Schott
M Schott
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
J Schovancova
J Schovancova
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
S Schramm
S Schramm
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
M Schreyer
M Schreyer
226Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
226,
N Schuh
N Schuh
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
M J Schultens
M J Schultens
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
H -C Schultz-Coulon
H -C Schultz-Coulon
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
H Schulz
H Schulz
19Department of Physics, Humboldt University, Berlin, Germany
19,
M Schumacher
M Schumacher
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
B A Schumm
B A Schumm
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
Ph Schune
Ph Schune
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
A Schwartzman
A Schwartzman
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
T A Schwarz
T A Schwarz
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
Ph Schwegler
Ph Schwegler
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
H Schweiger
H Schweiger
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
Ph Schwemling
Ph Schwemling
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
R Schwienhorst
R Schwienhorst
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
J Schwindling
J Schwindling
182DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
182,
T Schwindt
T Schwindt
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
G Sciolla
G Sciolla
31Department of Physics, Brandeis University, Waltham, MA USA
31,
F Scuri
F Scuri
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
F Scutti
F Scutti
118School of Physics, University of Melbourne, Victoria, Australia
118,
J Searcy
J Searcy
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
P Seema
P Seema
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
S C Seidel
S C Seidel
136Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
136,
A Seiden
A Seiden
183Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA USA
183,
F Seifert
F Seifert
167Czech Technical University in Prague, Prague, Czech Republic
167,
J M Seixas
J M Seixas
32Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
32,
G Sekhniaidze
G Sekhniaidze
134INFN Sezione di Napoli, Naples, Italy
134,
K Sekhon
K Sekhon
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
S J Sekula
S J Sekula
63Physics Department, Southern Methodist University, Dallas, TX USA
63,
D M Seliverstov
D M Seliverstov
1Department of Physics, University of Adelaide, Adelaide, Australia
155National Research Centre “Kurchatov Institute” B.P. Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
1,155,
N Semprini-Cesari
N Semprini-Cesari
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
C Serfon
C Serfon
150Department of Physics, University of Oslo, Oslo, Norway
150,
L Serin
L Serin
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
L Serkin
L Serkin
214INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
215ICTP, Trieste, Italy
214,215,
M Sessa
M Sessa
175INFN Sezione di Roma Tre, Rome, Italy
176Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
175,176,
R Seuster
R Seuster
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
H Severini
H Severini
144Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
144,
T Sfiligoj
T Sfiligoj
105Department of Physics, Jožef Stefan Institute, University of Ljubljana, Ljubljana, Slovenia
105,
F Sforza
F Sforza
45CERN, Geneva, Switzerland
45,
A Sfyrla
A Sfyrla
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
E Shabalina
E Shabalina
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
N W Shaikh
N W Shaikh
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
L Y Shan
L Y Shan
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
R Shang
R Shang
218Department of Physics, University of Illinois, Urbana, IL USA
218,
J T Shank
J T Shank
30Department of Physics, Boston University, Boston, MA USA
30,
M Shapiro
M Shapiro
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
P B Shatalov
P B Shatalov
127Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
127,
K Shaw
K Shaw
214INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
215ICTP, Trieste, Italy
214,215,
S M Shaw
S M Shaw
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
A Shcherbakova
A Shcherbakova
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
C Y Shehu
C Y Shehu
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
P Sherwood
P Sherwood
108Department of Physics and Astronomy, University College London, London, UK
108,
L Shi
L Shi
201Institute of Physics, Academia Sinica, Taipei, Taiwan
201,
S Shimizu
S Shimizu
96Graduate School of Science, Kobe University, Kobe, Japan
96,
C O Shimmin
C O Shimmin
213Department of Physics and Astronomy, University of California Irvine, Irvine, CA USA
213,
M Shimojima
M Shimojima
132Nagasaki Institute of Applied Science, Nagasaki, Japan
132,
M Shiyakova
M Shiyakova
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
A Shmeleva
A Shmeleva
126P.N. Lebedev Physical Institute of the Russian, Academy of Sciences, Moscow, Russia
126,
D Shoaleh Saadi
D Shoaleh Saadi
125Group of Particle Physics, University of Montreal, Montreal, QC Canada
125,
M J Shochet
M J Shochet
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
S Shojaii
S Shojaii
121INFN Sezione di Milano, Milan, Italy
122Dipartimento di Fisica, Università di Milano, Milan, Italy
121,122,
S Shrestha
S Shrestha
142Ohio State University, Columbus, OH USA
142,
E Shulga
E Shulga
128National Research Nuclear University MEPhI, Moscow, Russia
128,
M A Shupe
M A Shupe
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
P Sicho
P Sicho
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
A M Sickles
A M Sickles
218Department of Physics, University of Illinois, Urbana, IL USA
218,
P E Sidebo
P E Sidebo
197Physics Department, Royal Institute of Technology, Stockholm, Sweden
197,
O Sidiropoulou
O Sidiropoulou
226Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
226,
D Sidorov
D Sidorov
145Department of Physics, Oklahoma State University, Stillwater, OK USA
145,
A Sidoti
A Sidoti
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
F Siegert
F Siegert
67Institut für Kern–und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
67,
Dj Sijacki
Dj Sijacki
16Institute of Physics, University of Belgrade, Belgrade, Serbia
16,
J Silva
J Silva
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
162Centro de Física Nuclear da Universidade de Lisboa, Lisbon, Portugal
159,162,
S B Silverstein
S B Silverstein
195Department of Physics, Stockholm University, Stockholm, Sweden
195,
V Simak
V Simak
167Czech Technical University in Prague, Prague, Czech Republic
167,
O Simard
O Simard
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
Lj Simic
Lj Simic
16Institute of Physics, University of Belgrade, Belgrade, Serbia
16,
S Simion
S Simion
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
E Simioni
E Simioni
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
B Simmons
B Simmons
108Department of Physics and Astronomy, University College London, London, UK
108,
D Simon
D Simon
55Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
55,
M Simon
M Simon
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
P Sinervo
P Sinervo
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
N B Sinev
N B Sinev
147Center for High Energy Physics, University of Oregon, Eugene, OR USA
147,
M Sioli
M Sioli
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
G Siragusa
G Siragusa
226Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
226,
S Yu Sivoklokov
S Yu Sivoklokov
129D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
129,
J Sjölin
J Sjölin
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
T B Sjursen
T B Sjursen
17Department for Physics and Technology, University of Bergen, Bergen, Norway
17,
M B Skinner
M B Skinner
101Physics Department, Lancaster University, Lancaster, UK
101,
H P Skottowe
H P Skottowe
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
P Skubic
P Skubic
144Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
144,
M Slater
M Slater
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
T Slavicek
T Slavicek
167Czech Technical University in Prague, Prague, Czech Republic
167,
M Slawinska
M Slawinska
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
K Sliwa
K Sliwa
212Department of Physics and Astronomy, Tufts University, Medford, MA United States of America
212,
R Slovak
R Slovak
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
V Smakhtin
V Smakhtin
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
B H Smart
B H Smart
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
L Smestad
L Smestad
17Department for Physics and Technology, University of Bergen, Bergen, Norway
17,
J Smiesko
J Smiesko
190Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
190,
S Yu Smirnov
S Yu Smirnov
128National Research Nuclear University MEPhI, Moscow, Russia
128,
Y Smirnov
Y Smirnov
128National Research Nuclear University MEPhI, Moscow, Russia
128,
L N Smirnova
L N Smirnova
129D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
129,
O Smirnova
O Smirnova
111Fysiska institutionen, Lunds universitet, Lund, Sweden
111,
M N K Smith
M N K Smith
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
R W Smith
R W Smith
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
M Smizanska
M Smizanska
101Physics Department, Lancaster University, Lancaster, UK
101,
K Smolek
K Smolek
167Czech Technical University in Prague, Prague, Czech Republic
167,
A A Snesarev
A A Snesarev
126P.N. Lebedev Physical Institute of the Russian, Academy of Sciences, Moscow, Russia
126,
S Snyder
S Snyder
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
R Sobie
R Sobie
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
F Socher
F Socher
67Institut für Kern–und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
67,
A Soffer
A Soffer
203Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
203,
D A Soh
D A Soh
201Institute of Physics, Academia Sinica, Taipei, Taiwan
201,
G Sokhrannyi
G Sokhrannyi
105Department of Physics, Jožef Stefan Institute, University of Ljubljana, Ljubljana, Slovenia
105,
C A Solans Sanchez
C A Solans Sanchez
45CERN, Geneva, Switzerland
45,
M Solar
M Solar
167Czech Technical University in Prague, Prague, Czech Republic
167,
E Yu Soldatov
E Yu Soldatov
128National Research Nuclear University MEPhI, Moscow, Russia
128,
U Soldevila
U Soldevila
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
A A Solodkov
A A Solodkov
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
A Soloshenko
A Soloshenko
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
O V Solovyanov
O V Solovyanov
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
V Solovyev
V Solovyev
155National Research Centre “Kurchatov Institute” B.P. Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
155,
P Sommer
P Sommer
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
H Son
H Son
212Department of Physics and Astronomy, Tufts University, Medford, MA United States of America
212,
H Y Song
H Y Song
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
A Sood
A Sood
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
A Sopczak
A Sopczak
167Czech Technical University in Prague, Prague, Czech Republic
167,
V Sopko
V Sopko
167Czech Technical University in Prague, Prague, Czech Republic
167,
V Sorin
V Sorin
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
D Sosa
D Sosa
84Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
84,
C L Sotiropoulou
C L Sotiropoulou
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
R Soualah
R Soualah
214INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
216Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
214,216,
A M Soukharev
A M Soukharev
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
D South
D South
65DESY, Hamburg and Zeuthen, Germany
65,
B C Sowden
B C Sowden
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
S Spagnolo
S Spagnolo
102INFN Sezione di Lecce, Lecce, Italy
103Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
102,103,
M Spalla
M Spalla
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
M Spangenberg
M Spangenberg
222Department of Physics, University of Warwick, Coventry, UK
222,
F Spanò
F Spanò
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
D Sperlich
D Sperlich
19Department of Physics, Humboldt University, Berlin, Germany
19,
F Spettel
F Spettel
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
R Spighi
R Spighi
27INFN Sezione di Bologna, Bologna, Italy
27,
G Spigo
G Spigo
45CERN, Geneva, Switzerland
45,
L A Spiller
L A Spiller
118School of Physics, University of Melbourne, Victoria, Australia
118,
M Spousta
M Spousta
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
R D St Denis
R D St Denis
1Department of Physics, University of Adelaide, Adelaide, Australia
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
1,78,
A Stabile
A Stabile
121INFN Sezione di Milano, Milan, Italy
121,
R Stamen
R Stamen
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
S Stamm
S Stamm
19Department of Physics, Humboldt University, Berlin, Germany
19,
E Stanecka
E Stanecka
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
R W Stanek
R W Stanek
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
C Stanescu
C Stanescu
175INFN Sezione di Roma Tre, Rome, Italy
175,
M Stanescu-Bellu
M Stanescu-Bellu
65DESY, Hamburg and Zeuthen, Germany
65,
M M Stanitzki
M M Stanitzki
65DESY, Hamburg and Zeuthen, Germany
65,
S Stapnes
S Stapnes
150Department of Physics, University of Oslo, Oslo, Norway
150,
E A Starchenko
E A Starchenko
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
G H Stark
G H Stark
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
J Stark
J Stark
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
P Staroba
P Staroba
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
P Starovoitov
P Starovoitov
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
S Stärz
S Stärz
45CERN, Geneva, Switzerland
45,
R Staszewski
R Staszewski
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
P Steinberg
P Steinberg
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
B Stelzer
B Stelzer
188Department of Physics, Simon Fraser University, Burnaby, BC Canada
188,
H J Stelzer
H J Stelzer
45CERN, Geneva, Switzerland
45,
O Stelzer-Chilton
O Stelzer-Chilton
209TRIUMF, Vancouver, BC Canada
209,
H Stenzel
H Stenzel
77II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
77,
G A Stewart
G A Stewart
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
J A Stillings
J A Stillings
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
M C Stockton
M C Stockton
117Department of Physics, McGill University, Montreal, QC Canada
117,
M Stoebe
M Stoebe
117Department of Physics, McGill University, Montreal, QC Canada
117,
G Stoicea
G Stoicea
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
P Stolte
P Stolte
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
S Stonjek
S Stonjek
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
A R Stradling
A R Stradling
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
A Straessner
A Straessner
67Institut für Kern–und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
67,
M E Stramaglia
M E Stramaglia
20Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
20,
J Strandberg
J Strandberg
197Physics Department, Royal Institute of Technology, Stockholm, Sweden
197,
S Strandberg
S Strandberg
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
A Strandlie
A Strandlie
150Department of Physics, University of Oslo, Oslo, Norway
150,
M Strauss
M Strauss
144Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
144,
P Strizenec
P Strizenec
191Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
191,
R Ströhmer
R Ströhmer
226Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
226,
D M Strom
D M Strom
147Center for High Energy Physics, University of Oregon, Eugene, OR USA
147,
R Stroynowski
R Stroynowski
63Physics Department, Southern Methodist University, Dallas, TX USA
63,
A Strubig
A Strubig
137Institute for Mathematics Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
137,
S A Stucci
S A Stucci
20Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
20,
B Stugu
B Stugu
17Department for Physics and Technology, University of Bergen, Bergen, Norway
17,
N A Styles
N A Styles
65DESY, Hamburg and Zeuthen, Germany
65,
D Su
D Su
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
J Su
J Su
158Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
158,
R Subramaniam
R Subramaniam
109Louisiana Tech University, Ruston, LA USA
109,
S Suchek
S Suchek
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
Y Sugaya
Y Sugaya
149Graduate School of Science, Osaka University, Osaka, Japan
149,
M Suk
M Suk
167Czech Technical University in Prague, Prague, Czech Republic
167,
V V Sulin
V V Sulin
126P.N. Lebedev Physical Institute of the Russian, Academy of Sciences, Moscow, Russia
126,
S Sultansoy
S Sultansoy
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
T Sumida
T Sumida
97Faculty of Science, Kyoto University, Kyoto, Japan
97,
S Sun
S Sun
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
X Sun
X Sun
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
J E Sundermann
J E Sundermann
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
K Suruliz
K Suruliz
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
G Susinno
G Susinno
58INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Cosenza, Italy
59Dipartimento di Fisica, Università della Calabria, Rende, Italy
58,59,
M R Sutton
M R Sutton
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
S Suzuki
S Suzuki
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
M Svatos
M Svatos
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
M Swiatlowski
M Swiatlowski
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
I Sykora
I Sykora
190Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
190,
T Sykora
T Sykora
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
D Ta
D Ta
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
C Taccini
C Taccini
175INFN Sezione di Roma Tre, Rome, Italy
176Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
175,176,
K Tackmann
K Tackmann
65DESY, Hamburg and Zeuthen, Germany
65,
J Taenzer
J Taenzer
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
A Taffard
A Taffard
213Department of Physics and Astronomy, University of California Irvine, Irvine, CA USA
213,
R Tafirout
R Tafirout
209TRIUMF, Vancouver, BC Canada
209,
N Taiblum
N Taiblum
203Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
203,
H Takai
H Takai
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
R Takashima
R Takashima
98Kyoto University of Education, Kyoto, Japan
98,
T Takeshita
T Takeshita
186Department of Physics, Shinshu University, Nagano, Japan
186,
Y Takubo
Y Takubo
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
M Talby
M Talby
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
A A Talyshev
A A Talyshev
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
K G Tan
K G Tan
118School of Physics, University of Melbourne, Victoria, Australia
118,
J Tanaka
J Tanaka
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
R Tanaka
R Tanaka
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
S Tanaka
S Tanaka
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
B B Tannenwald
B B Tannenwald
142Ohio State University, Columbus, OH USA
142,
S Tapia Araya
S Tapia Araya
48Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
48,
S Tapprogge
S Tapprogge
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
S Tarem
S Tarem
202Department of Physics, Technion: Israel Institute of Technology, Haifa, Israel
202,
G F Tartarelli
G F Tartarelli
121INFN Sezione di Milano, Milan, Italy
121,
P Tas
P Tas
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
M Tasevsky
M Tasevsky
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
T Tashiro
T Tashiro
97Faculty of Science, Kyoto University, Kyoto, Japan
97,
E Tassi
E Tassi
58INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Cosenza, Italy
59Dipartimento di Fisica, Università della Calabria, Rende, Italy
58,59,
A Tavares Delgado
A Tavares Delgado
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
160Faculdade de Ciências, Universidade de Lisboa, Lisbon, Portugal
159,160,
Y Tayalati
Y Tayalati
180Faculté des Sciences, Université Mohamed Premier and LPTPM, Oujda, Morocco
180,
A C Taylor
A C Taylor
136Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
136,
G N Taylor
G N Taylor
118School of Physics, University of Melbourne, Victoria, Australia
118,
P T E Taylor
P T E Taylor
118School of Physics, University of Melbourne, Victoria, Australia
118,
W Taylor
W Taylor
210Department of Physics and Astronomy, York University, Toronto, ON Canada
210,
F A Teischinger
F A Teischinger
45CERN, Geneva, Switzerland
45,
P Teixeira-Dias
P Teixeira-Dias
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
K K Temming
K K Temming
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
D Temple
D Temple
188Department of Physics, Simon Fraser University, Burnaby, BC Canada
188,
H Ten Kate
H Ten Kate
45CERN, Geneva, Switzerland
45,
P K Teng
P K Teng
201Institute of Physics, Academia Sinica, Taipei, Taiwan
201,
J J Teoh
J J Teoh
149Graduate School of Science, Osaka University, Osaka, Japan
149,
F Tepel
F Tepel
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
S Terada
S Terada
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
K Terashi
K Terashi
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
J Terron
J Terron
112Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
112,
S Terzo
S Terzo
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
M Testa
M Testa
70INFN Laboratori Nazionali di Frascati, Frascati, Italy
70,
R J Teuscher
R J Teuscher
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
T Theveneaux-Pelzer
T Theveneaux-Pelzer
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
J P Thomas
J P Thomas
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
J Thomas-Wilsker
J Thomas-Wilsker
107Department of Physics, Royal Holloway University of London, Surrey, UK
107,
E N Thompson
E N Thompson
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
P D Thompson
P D Thompson
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
A S Thompson
A S Thompson
78SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
78,
L A Thomsen
L A Thomsen
228Department of Physics, Yale University, New Haven, CT USA
228,
E Thomson
E Thomson
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
M Thomson
M Thomson
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
M J Tibbetts
M J Tibbetts
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
R E Ticse Torres
R E Ticse Torres
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
V O Tikhomirov
V O Tikhomirov
126P.N. Lebedev Physical Institute of the Russian, Academy of Sciences, Moscow, Russia
126,
Yu A Tikhonov
Yu A Tikhonov
140Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
140,
S Timoshenko
S Timoshenko
128National Research Nuclear University MEPhI, Moscow, Russia
128,
P Tipton
P Tipton
228Department of Physics, Yale University, New Haven, CT USA
228,
S Tisserant
S Tisserant
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
K Todome
K Todome
207Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
207,
T Todorov
T Todorov
1Department of Physics, University of Adelaide, Adelaide, Australia
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
1,7,
S Todorova-Nova
S Todorova-Nova
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
J Tojo
J Tojo
99Department of Physics, Kyushu University, Fukuoka, Japan
99,
S Tokár
S Tokár
190Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
190,
K Tokushuku
K Tokushuku
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
E Tolley
E Tolley
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
L Tomlinson
L Tomlinson
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
M Tomoto
M Tomoto
133Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
133,
L Tompkins
L Tompkins
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
K Toms
K Toms
136Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
136,
B Tong
B Tong
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
E Torrence
E Torrence
147Center for High Energy Physics, University of Oregon, Eugene, OR USA
147,
H Torres
H Torres
188Department of Physics, Simon Fraser University, Burnaby, BC Canada
188,
E Torró Pastor
E Torró Pastor
184Department of Physics, University of Washington, Seattle, WA USA
184,
J Toth
J Toth
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
F Touchard
F Touchard
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
D R Tovey
D R Tovey
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
T Trefzger
T Trefzger
226Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
226,
A Tricoli
A Tricoli
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
I M Trigger
I M Trigger
209TRIUMF, Vancouver, BC Canada
209,
S Trincaz-Duvoid
S Trincaz-Duvoid
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
M F Tripiana
M F Tripiana
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
W Trischuk
W Trischuk
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
B Trocmé
B Trocmé
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
A Trofymov
A Trofymov
65DESY, Hamburg and Zeuthen, Germany
65,
C Troncon
C Troncon
121INFN Sezione di Milano, Milan, Italy
121,
M Trottier-McDonald
M Trottier-McDonald
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
M Trovatelli
M Trovatelli
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
L Truong
L Truong
214INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
216Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
214,216,
M Trzebinski
M Trzebinski
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
A Trzupek
A Trzupek
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
J C-L Tseng
J C-L Tseng
151Department of Physics, Oxford University, Oxford, UK
151,
P V Tsiareshka
P V Tsiareshka
123B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
123,
G Tsipolitis
G Tsipolitis
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
N Tsirintanis
N Tsirintanis
11Physics Department, University of Athens, Athens, Greece
11,
S Tsiskaridze
S Tsiskaridze
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
V Tsiskaridze
V Tsiskaridze
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
E G Tskhadadze
E G Tskhadadze
75E. Andronikashvili Institute of Physics, Iv. Javakhishvili Tbilisi State University, Tbilisi, Georgia
75,
K M Tsui
K M Tsui
87Department of Physics, The Chinese University of Hong Kong, Shatin, NT Hong Kong
87,
I I Tsukerman
I I Tsukerman
127Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
127,
V Tsulaia
V Tsulaia
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
S Tsuno
S Tsuno
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
D Tsybychev
D Tsybychev
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
A Tudorache
A Tudorache
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
V Tudorache
V Tudorache
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
A N Tuna
A N Tuna
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
S A Tupputi
S A Tupputi
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
S Turchikhin
S Turchikhin
129D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
129,
D Turecek
D Turecek
167Czech Technical University in Prague, Prague, Czech Republic
167,
D Turgeman
D Turgeman
224Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
224,
R Turra
R Turra
121INFN Sezione di Milano, Milan, Italy
122Dipartimento di Fisica, Università di Milano, Milan, Italy
121,122,
A J Turvey
A J Turvey
63Physics Department, Southern Methodist University, Dallas, TX USA
63,
P M Tuts
P M Tuts
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
M Tyndel
M Tyndel
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
G Ucchielli
G Ucchielli
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
I Ueda
I Ueda
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
R Ueno
R Ueno
44Department of Physics, Carleton University, Ottawa, ON Canada
44,
M Ughetto
M Ughetto
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
F Ukegawa
F Ukegawa
211Faculty of Pure and Applied Sciences, and Center for Integrated Research in Fundamental Science and Engineering, University of Tsukuba, Tsukuba, Japan
211,
G Unal
G Unal
45CERN, Geneva, Switzerland
45,
A Undrus
A Undrus
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
G Unel
G Unel
213Department of Physics and Astronomy, University of California Irvine, Irvine, CA USA
213,
F C Ungaro
F C Ungaro
118School of Physics, University of Melbourne, Victoria, Australia
118,
Y Unno
Y Unno
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
C Unverdorben
C Unverdorben
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
J Urban
J Urban
191Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
191,
P Urquijo
P Urquijo
118School of Physics, University of Melbourne, Victoria, Australia
118,
P Urrejola
P Urrejola
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
G Usai
G Usai
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
A Usanova
A Usanova
91Institut für Astro–und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
91,
L Vacavant
L Vacavant
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
115,
V Vacek
V Vacek
167Czech Technical University in Prague, Prague, Czech Republic
167,
B Vachon
B Vachon
117Department of Physics, McGill University, Montreal, QC Canada
117,
C Valderanis
C Valderanis
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
E Valdes Santurio
E Valdes Santurio
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
N Valencic
N Valencic
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
S Valentinetti
S Valentinetti
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
A Valero
A Valero
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
L Valery
L Valery
15Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
15,
S Valkar
S Valkar
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
S Vallecorsa
S Vallecorsa
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
J A Valls Ferrer
J A Valls Ferrer
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
W Van Den Wollenberg
W Van Den Wollenberg
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
P C Van Der Deijl
P C Van Der Deijl
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
R van der Geer
R van der Geer
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
H van der Graaf
H van der Graaf
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
N van Eldik
N van Eldik
202Department of Physics, Technion: Israel Institute of Technology, Haifa, Israel
202,
P van Gemmeren
P van Gemmeren
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
J Van Nieuwkoop
J Van Nieuwkoop
188Department of Physics, Simon Fraser University, Burnaby, BC Canada
188,
I van Vulpen
I van Vulpen
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
M C van Woerden
M C van Woerden
45CERN, Geneva, Switzerland
45,
M Vanadia
M Vanadia
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
W Vandelli
W Vandelli
45CERN, Geneva, Switzerland
45,
R Vanguri
R Vanguri
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
A Vaniachine
A Vaniachine
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
P Vankov
P Vankov
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
G Vardanyan
G Vardanyan
229Yerevan Physics Institute, Yerevan, Armenia
229,
R Vari
R Vari
171INFN Sezione di Roma, Rome, Italy
171,
E W Varnes
E W Varnes
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
T Varol
T Varol
63Physics Department, Southern Methodist University, Dallas, TX USA
63,
D Varouchas
D Varouchas
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
A Vartapetian
A Vartapetian
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
K E Varvell
K E Varvell
200School of Physics, University of Sydney, Sydney, Australia
200,
J G Vasquez
J G Vasquez
228Department of Physics, Yale University, New Haven, CT USA
228,
F Vazeille
F Vazeille
55Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
55,
T Vazquez Schroeder
T Vazquez Schroeder
117Department of Physics, McGill University, Montreal, QC Canada
117,
J Veatch
J Veatch
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
L M Veloce
L M Veloce
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
F Veloso
F Veloso
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
161Department of Physics, University of Coimbra, Coimbra, Portugal
159,161,
S Veneziano
S Veneziano
171INFN Sezione di Roma, Rome, Italy
171,
A Ventura
A Ventura
102INFN Sezione di Lecce, Lecce, Italy
103Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
102,103,
M Venturi
M Venturi
221Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
221,
N Venturi
N Venturi
208Department of Physics, University of Toronto, Toronto, ON Canada
208,
A Venturini
A Venturini
31Department of Physics, Brandeis University, Waltham, MA USA
31,
V Vercesi
V Vercesi
152INFN Sezione di Pavia, Pavia, Italy
152,
M Verducci
M Verducci
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
W Verkerke
W Verkerke
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
J C Vermeulen
J C Vermeulen
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
A Vest
A Vest
67Institut für Kern–und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
67,
M C Vetterli
M C Vetterli
188Department of Physics, Simon Fraser University, Burnaby, BC Canada
188,
O Viazlo
O Viazlo
111Fysiska institutionen, Lunds universitet, Lund, Sweden
111,
I Vichou
I Vichou
1Department of Physics, University of Adelaide, Adelaide, Australia
218Department of Physics, University of Illinois, Urbana, IL USA
1,218,
T Vickey
T Vickey
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
O E Vickey Boeriu
O E Vickey Boeriu
185Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
185,
G H A Viehhauser
G H A Viehhauser
151Department of Physics, Oxford University, Oxford, UK
151,
S Viel
S Viel
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
L Vigani
L Vigani
151Department of Physics, Oxford University, Oxford, UK
151,
R Vigne
R Vigne
91Institut für Astro–und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
91,
M Villa
M Villa
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
M Villaplana Perez
M Villaplana Perez
121INFN Sezione di Milano, Milan, Italy
122Dipartimento di Fisica, Università di Milano, Milan, Italy
121,122,
E Vilucchi
E Vilucchi
70INFN Laboratori Nazionali di Frascati, Frascati, Italy
70,
M G Vincter
M G Vincter
44Department of Physics, Carleton University, Ottawa, ON Canada
44,
V B Vinogradov
V B Vinogradov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
C Vittori
C Vittori
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
I Vivarelli
I Vivarelli
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
S Vlachos
S Vlachos
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
M Vlasak
M Vlasak
167Czech Technical University in Prague, Prague, Czech Republic
167,
M Vogel
M Vogel
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
P Vokac
P Vokac
167Czech Technical University in Prague, Prague, Czech Republic
167,
G Volpi
G Volpi
156INFN Sezione di Pisa, Pisa, Italy
157Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
156,157,
M Volpi
M Volpi
118School of Physics, University of Melbourne, Victoria, Australia
118,
H von der Schmitt
H von der Schmitt
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
E von Toerne
E von Toerne
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
V Vorobel
V Vorobel
168Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic
168,
K Vorobev
K Vorobev
128National Research Nuclear University MEPhI, Moscow, Russia
128,
M Vos
M Vos
219Instituto de Fisica Corpuscular (IFIC) and Departamento de Fisica Atomica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
219,
R Voss
R Voss
45CERN, Geneva, Switzerland
45,
J H Vossebeld
J H Vossebeld
104Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
104,
N Vranjes
N Vranjes
16Institute of Physics, University of Belgrade, Belgrade, Serbia
16,
M Vranjes Milosavljevic
M Vranjes Milosavljevic
16Institute of Physics, University of Belgrade, Belgrade, Serbia
16,
V Vrba
V Vrba
166Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
166,
M Vreeswijk
M Vreeswijk
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
R Vuillermet
R Vuillermet
45CERN, Geneva, Switzerland
45,
I Vukotic
I Vukotic
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
Z Vykydal
Z Vykydal
167Czech Technical University in Prague, Prague, Czech Republic
167,
P Wagner
P Wagner
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
W Wagner
W Wagner
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
H Wahlberg
H Wahlberg
100Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
100,
S Wahrmund
S Wahrmund
67Institut für Kern–und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
67,
J Wakabayashi
J Wakabayashi
133Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
133,
J Walder
J Walder
101Physics Department, Lancaster University, Lancaster, UK
101,
R Walker
R Walker
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
W Walkowiak
W Walkowiak
187Fachbereich Physik, Universität Siegen, Siegen, Germany
187,
V Wallangen
V Wallangen
195Department of Physics, Stockholm University, Stockholm, Sweden
196The Oskar Klein Centre, Stockholm, Sweden
195,196,
C Wang
C Wang
51Department of Physics, Nanjing University, Jiangsu, China
51,
C Wang
C Wang
52School of Physics, Shandong University, Shandong, China
115CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
52,115,
F Wang
F Wang
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
H Wang
H Wang
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
H Wang
H Wang
63Physics Department, Southern Methodist University, Dallas, TX USA
63,
J Wang
J Wang
65DESY, Hamburg and Zeuthen, Germany
65,
J Wang
J Wang
200School of Physics, University of Sydney, Sydney, Australia
200,
K Wang
K Wang
117Department of Physics, McGill University, Montreal, QC Canada
117,
R Wang
R Wang
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
S M Wang
S M Wang
201Institute of Physics, Academia Sinica, Taipei, Taiwan
201,
T Wang
T Wang
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
T Wang
T Wang
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
W Wang
W Wang
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
X Wang
X Wang
228Department of Physics, Yale University, New Haven, CT USA
228,
C Wanotayaroj
C Wanotayaroj
147Center for High Energy Physics, University of Oregon, Eugene, OR USA
147,
A Warburton
A Warburton
117Department of Physics, McGill University, Montreal, QC Canada
117,
C P Ward
C P Ward
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
D R Wardrope
D R Wardrope
108Department of Physics and Astronomy, University College London, London, UK
108,
A Washbrook
A Washbrook
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
P M Watkins
P M Watkins
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
A T Watson
A T Watson
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
M F Watson
M F Watson
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
G Watts
G Watts
184Department of Physics, University of Washington, Seattle, WA USA
184,
S Watts
S Watts
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
B M Waugh
B M Waugh
108Department of Physics and Astronomy, University College London, London, UK
108,
S Webb
S Webb
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
M S Weber
M S Weber
20Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
20,
S W Weber
S W Weber
226Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
226,
J S Webster
J S Webster
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
A R Weidberg
A R Weidberg
151Department of Physics, Oxford University, Oxford, UK
151,
B Weinert
B Weinert
90Department of Physics, Indiana University, Bloomington, IN USA
90,
J Weingarten
J Weingarten
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
C Weiser
C Weiser
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
H Weits
H Weits
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
P S Wells
P S Wells
45CERN, Geneva, Switzerland
45,
T Wenaus
T Wenaus
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
T Wengler
T Wengler
45CERN, Geneva, Switzerland
45,
S Wenig
S Wenig
45CERN, Geneva, Switzerland
45,
N Wermes
N Wermes
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
M Werner
M Werner
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
M D Werner
M D Werner
93Department of Physics and Astronomy, Iowa State University, Ames, IA USA
93,
P Werner
P Werner
45CERN, Geneva, Switzerland
45,
M Wessels
M Wessels
83Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
83,
J Wetter
J Wetter
212Department of Physics and Astronomy, Tufts University, Medford, MA United States of America
212,
K Whalen
K Whalen
147Center for High Energy Physics, University of Oregon, Eugene, OR USA
147,
N L Whallon
N L Whallon
184Department of Physics, University of Washington, Seattle, WA USA
184,
A M Wharton
A M Wharton
101Physics Department, Lancaster University, Lancaster, UK
101,
A White
A White
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
M J White
M J White
1Department of Physics, University of Adelaide, Adelaide, Australia
1,
R White
R White
48Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
48,
D Whiteson
D Whiteson
213Department of Physics and Astronomy, University of California Irvine, Irvine, CA USA
213,
F J Wickens
F J Wickens
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
W Wiedenmann
W Wiedenmann
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
M Wielers
M Wielers
170Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
170,
P Wienemann
P Wienemann
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
C Wiglesworth
C Wiglesworth
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
L A M Wiik-Fuchs
L A M Wiik-Fuchs
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
A Wildauer
A Wildauer
131Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
131,
F Wilk
F Wilk
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
H G Wilkens
H G Wilkens
45CERN, Geneva, Switzerland
45,
H H Williams
H H Williams
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
S Williams
S Williams
138Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
138,
C Willis
C Willis
120Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
120,
S Willocq
S Willocq
116Department of Physics, University of Massachusetts, Amherst, MA USA
116,
J A Wilson
J A Wilson
21School of Physics and Astronomy, University of Birmingham, Birmingham, UK
21,
I Wingerter-Seez
I Wingerter-Seez
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
F Winklmeier
F Winklmeier
147Center for High Energy Physics, University of Oregon, Eugene, OR USA
147,
O J Winston
O J Winston
199Department of Physics and Astronomy, University of Sussex, Brighton, UK
199,
B T Winter
B T Winter
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
M Wittgen
M Wittgen
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
J Wittkowski
J Wittkowski
130Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
130,
S J Wollstadt
S J Wollstadt
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
M W Wolter
M W Wolter
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
H Wolters
H Wolters
159Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
161Department of Physics, University of Coimbra, Coimbra, Portugal
159,161,
B K Wosiek
B K Wosiek
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
J Wotschack
J Wotschack
45CERN, Geneva, Switzerland
45,
M J Woudstra
M J Woudstra
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
K W Wozniak
K W Wozniak
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
M Wu
M Wu
80Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
80,
M Wu
M Wu
46Enrico Fermi Institute, University of Chicago, Chicago, IL USA
46,
S L Wu
S L Wu
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
X Wu
X Wu
72Section de Physique, Université de Genève, Geneva, Switzerland
72,
Y Wu
Y Wu
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
T R Wyatt
T R Wyatt
114School of Physics and Astronomy, University of Manchester, Manchester, UK
114,
B M Wynne
B M Wynne
69SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
69,
S Xella
S Xella
57Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
57,
D Xu
D Xu
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
L Xu
L Xu
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
B Yabsley
B Yabsley
200School of Physics, University of Sydney, Sydney, Australia
200,
S Yacoob
S Yacoob
192Department of Physics, University of Cape Town, Cape Town, South Africa
192,
R Yakabe
R Yakabe
96Graduate School of Science, Kobe University, Kobe, Japan
96,
D Yamaguchi
D Yamaguchi
207Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
207,
Y Yamaguchi
Y Yamaguchi
149Graduate School of Science, Osaka University, Osaka, Japan
149,
A Yamamoto
A Yamamoto
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
S Yamamoto
S Yamamoto
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
T Yamanaka
T Yamanaka
205International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
205,
K Yamauchi
K Yamauchi
133Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
133,
Y Yamazaki
Y Yamazaki
96Graduate School of Science, Kobe University, Kobe, Japan
96,
Z Yan
Z Yan
30Department of Physics, Boston University, Boston, MA USA
30,
H Yang
H Yang
53Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University (also affiliated with PKU-CHEP), Shanghai, China
53,
H Yang
H Yang
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
Y Yang
Y Yang
201Institute of Physics, Academia Sinica, Taipei, Taiwan
201,
Z Yang
Z Yang
17Department for Physics and Technology, University of Bergen, Bergen, Norway
17,
W-M Yao
W-M Yao
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
Y C Yap
Y C Yap
110Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
110,
Y Yasu
Y Yasu
95KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
95,
E Yatsenko
E Yatsenko
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
K H Yau Wong
K H Yau Wong
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
J Ye
J Ye
63Physics Department, Southern Methodist University, Dallas, TX USA
63,
S Ye
S Ye
36Physics Department, Brookhaven National Laboratory, Upton, NY USA
36,
I Yeletskikh
I Yeletskikh
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
A L Yen
A L Yen
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
E Yildirim
E Yildirim
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
K Yorita
K Yorita
223Waseda University, Tokyo, Japan
223,
R Yoshida
R Yoshida
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
K Yoshihara
K Yoshihara
154Department of Physics, University of Pennsylvania, Philadelphia, PA USA
154,
C Young
C Young
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
C J S Young
C J S Young
45CERN, Geneva, Switzerland
45,
S Youssef
S Youssef
30Department of Physics, Boston University, Boston, MA USA
30,
D R Yu
D R Yu
18Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA USA
18,
J Yu
J Yu
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
J M Yu
J M Yu
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
J Yu
J Yu
93Department of Physics and Astronomy, Iowa State University, Ames, IA USA
93,
L Yuan
L Yuan
96Graduate School of Science, Kobe University, Kobe, Japan
96,
S P Y Yuen
S P Y Yuen
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
I Yusuff
I Yusuff
43Cavendish Laboratory, University of Cambridge, Cambridge, UK
43,
B Zabinski
B Zabinski
62Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
62,
R Zaidan
R Zaidan
52School of Physics, Shandong University, Shandong, China
52,
A M Zaitsev
A M Zaitsev
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
N Zakharchuk
N Zakharchuk
65DESY, Hamburg and Zeuthen, Germany
65,
J Zalieckas
J Zalieckas
17Department for Physics and Technology, University of Bergen, Bergen, Norway
17,
A Zaman
A Zaman
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
S Zambito
S Zambito
82Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
82,
L Zanello
L Zanello
171INFN Sezione di Roma, Rome, Italy
172Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
171,172,
D Zanzi
D Zanzi
118School of Physics, University of Melbourne, Victoria, Australia
118,
C Zeitnitz
C Zeitnitz
227Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
227,
M Zeman
M Zeman
167Czech Technical University in Prague, Prague, Czech Republic
167,
A Zemla
A Zemla
60AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Kraków, Poland
60,
J C Zeng
J C Zeng
218Department of Physics, University of Illinois, Urbana, IL USA
218,
Q Zeng
Q Zeng
189SLAC National Accelerator Laboratory, Stanford, CA USA
189,
K Zengel
K Zengel
31Department of Physics, Brandeis University, Waltham, MA USA
31,
O Zenin
O Zenin
169State Research Center Institute for High Energy Physics (Protvino), NRC KI, Moscow, Russia
169,
T Ženiš
T Ženiš
190Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
190,
D Zerwas
D Zerwas
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
D Zhang
D Zhang
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
F Zhang
F Zhang
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
G Zhang
G Zhang
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
H Zhang
H Zhang
51Department of Physics, Nanjing University, Jiangsu, China
51,
J Zhang
J Zhang
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
L Zhang
L Zhang
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
R Zhang
R Zhang
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
R Zhang
R Zhang
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
X Zhang
X Zhang
52School of Physics, Shandong University, Shandong, China
52,
Z Zhang
Z Zhang
148LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
148,
X Zhao
X Zhao
63Physics Department, Southern Methodist University, Dallas, TX USA
63,
Y Zhao
Y Zhao
52School of Physics, Shandong University, Shandong, China
52,
Z Zhao
Z Zhao
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
A Zhemchugov
A Zhemchugov
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
J Zhong
J Zhong
151Department of Physics, Oxford University, Oxford, UK
151,
B Zhou
B Zhou
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
C Zhou
C Zhou
68Department of Physics, Duke University, Durham, NC USA
68,
L Zhou
L Zhou
56Nevis Laboratory, Columbia University, Irvington, NY USA
56,
L Zhou
L Zhou
63Physics Department, Southern Methodist University, Dallas, TX USA
63,
M Zhou
M Zhou
198Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY USA
198,
N Zhou
N Zhou
54Physics Department, Tsinghua University, Beijing, 100084 China
54,
C G Zhu
C G Zhu
52School of Physics, Shandong University, Shandong, China
52,
H Zhu
H Zhu
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
J Zhu
J Zhu
119Department of Physics, The University of Michigan, Ann Arbor, MI USA
119,
Y Zhu
Y Zhu
50Department of Modern Physics, University of Science and Technology of China, Anhui, China
50,
X Zhuang
X Zhuang
49Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
49,
K Zhukov
K Zhukov
126P.N. Lebedev Physical Institute of the Russian, Academy of Sciences, Moscow, Russia
126,
A Zibell
A Zibell
226Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
226,
D Zieminska
D Zieminska
90Department of Physics, Indiana University, Bloomington, IN USA
90,
N I Zimine
N I Zimine
94Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
94,
C Zimmermann
C Zimmermann
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
S Zimmermann
S Zimmermann
71Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
71,
Z Zinonos
Z Zinonos
79II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
79,
M Zinser
M Zinser
113Institut für Physik, Universität Mainz, Mainz, Germany
113,
M Ziolkowski
M Ziolkowski
187Fachbereich Physik, Universität Siegen, Siegen, Germany
187,
L Živković
L Živković
16Institute of Physics, University of Belgrade, Belgrade, Serbia
16,
G Zobernig
G Zobernig
225Department of Physics, University of Wisconsin, Madison, WI USA
225,
A Zoccoli
A Zoccoli
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
M zur Nedden
M zur Nedden
19Department of Physics, Humboldt University, Berlin, Germany
19,
G Zurzolo
G Zurzolo
134INFN Sezione di Napoli, Naples, Italy
135Dipartimento di Fisica, Università di Napoli, Naples, Italy
134,135,
L Zwalinski
L Zwalinski
45CERN, Geneva, Switzerland
45;
ATLAS Collaboration231