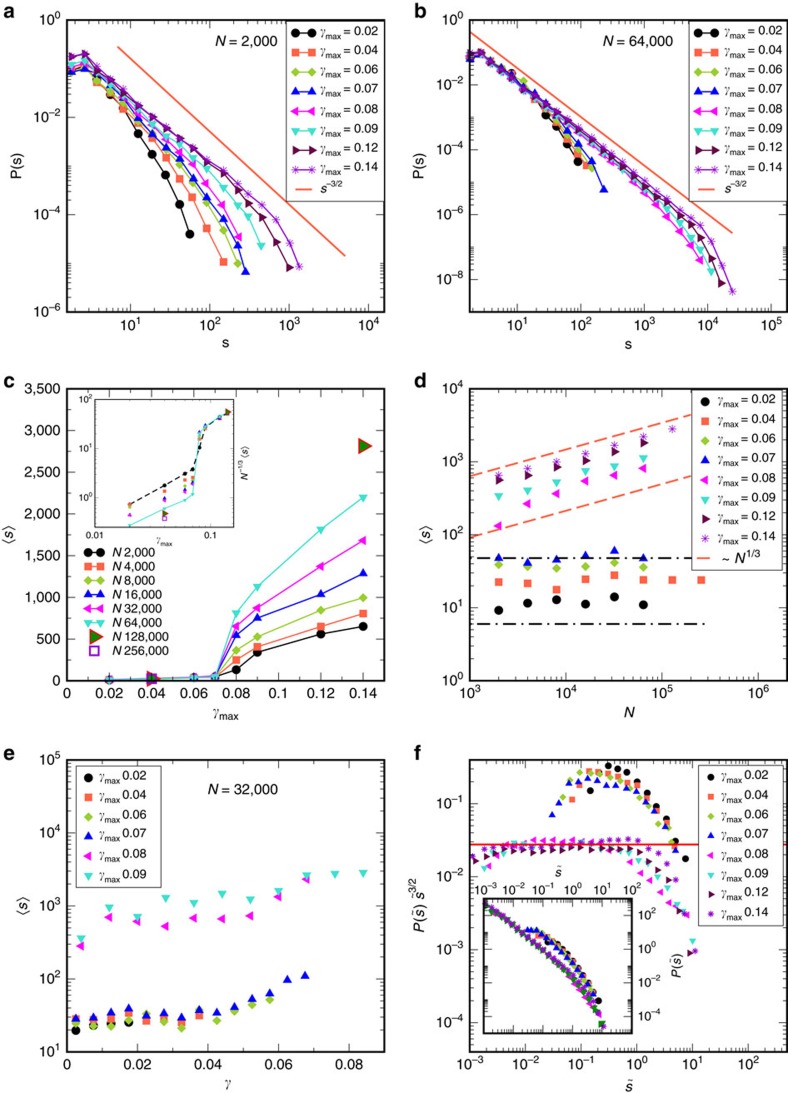
Figure 2. Statistics of avalanches as a function of strain amplitude γ_max and system size N.

(a) Cluster size distributions for N=2,000 displaying a power law with a cutoff that grows with γ_max but does not indicate sharp changes at yielding. (b) Cluster size distribution for N=64,000 displaying a sharp increase in the cutoff size across the yielding transition. The line in both panels corresponds to a power law with exponent −3/2. (c) Mean cluster size versus γ_max showing a qualitative change across the yielding transition, with strong system size dependence above γ_y. The inset shows the mean cluster size scaled with N^1/3, which describes well the size dependence above γ_y. (d) Mean cluster size versus system size N shows no significant size dependence for γ_max<γ_y but a clear N^1/3 dependence above. A crossover in behaviour is seen for γ_max=0.08. Lines, with N⁰ (constant) and N^1/3 dependence, are guides to the eye. (e) Mean cluster sizes for bins in strain γ for different γ_max for N=32,000. Mean cluster size does not depend on γ_max, and depends only mildly on strain γ, for two distinct sets, below and above yield strain γ_y. (f) Scaled cluster size 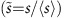distributions exhibit data collapse separately for γ_max<γ_y and γ_max>γ_y (inset). Distributions for γ_max<γ_y do not display a power law regime, whereas γ_max>γ_y do, over about two decades in 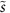, as highlighted in a plot of 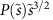versus 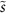. Data shown are for T=1, and averages are over the full cycle, except for (e) which are averaged over the first quadrant.