Figure 1.

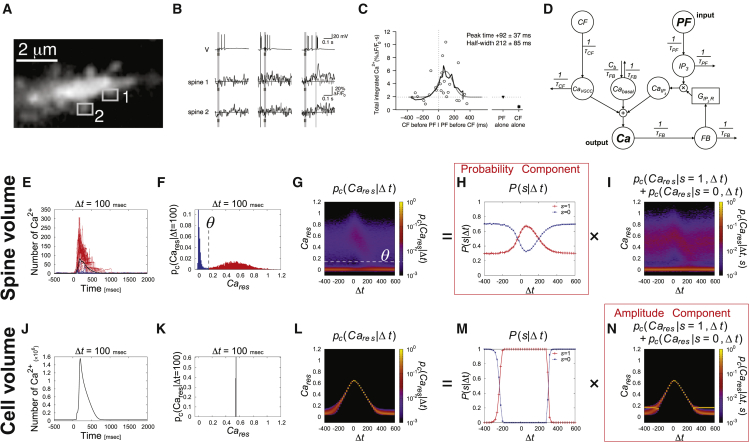
Information transfer of PF- and CF-timing by probability of Ca²⁺ increase in the simple stochastic model. (A–C) Experimental results of Ca²⁺ increase by PF and CF inputs at the spine in the cerebellar Purkinje cell (16). (A) Spines of the cerebellar Purkinje cell are shown. (B) Ca²⁺ responses in the indicated spines in (A) are shown. V indicates membrane potential and ΔF/F₀ indicates the normalized changes of the fluorescence probe of Ca²⁺. The left, middle, and right panels show the time courses with only the PF input (shaded vertical line), with the CF input (black vertical line) 60 ms before the PF input and with the PF input 60 ms before the CF input, respectively. (C) Total integrated Ca²⁺ with PF and CF inputs with various timing are shown. The gray line indicates the best fits of the raw data points to Gaussian functions. The black line indicates the box-smoothed average over three points. (D) The block diagram of the simple stochastic model in this study (see Materials and Methods) is provided. After Fig. 3, we set CF = 0 and used only PF as the input. Ca²⁺ increase in the spine volume (10⁻¹μm³) (E–I) and in the cell volume (10³μm³) (J–N) in the simple stochastic model. (E and J) Ca²⁺ increase with Δt = 100 ms is provided. Δt indicates the timing interval between PF and CF inputs, which is the timing of the PF input set as 0 and Δt with the PF input before CF input is positive, and vice versa. (E) The large Ca²⁺ increase (red) and small Ca²⁺ increase (blue) divided by θ in (F) are provided. (F and K) The probability density distribution of Ca_res is provided. Ca_res denotes the area under the curve of the time course of Ca²⁺, subtracted by the basal Ca²⁺ concentration, shown in (E) and (J). (F) The threshold θ is defined as the local minimum of the marginal distribution for Δt, given by $p_c\left(C{a}_{res}\right)={\int }_{\Delta t}{p}_c\left(C{a}_{res}|\tau \right)p_{in}\left(\tau \right)d\tau$ (see Fig. S1). (G and L) The probability density distribution of Ca_res in the spine volume (G) and cell volume (L) are provided. (H and M) The probability component of the distribution of Ca_res that exceeds the threshold $\theta$ in the spine volume (s = 1) (see Materials and Methods) is provided. Because the distribution of Ca_res in the cell volume is unimodal distribution, for convenience, we set θ = 0.157 in the cell volume, which is the same as that in the spine volume. (I and N) The amplitude component of the distribution of Ca_res (see Materials and Methods) is provided. Images are used with permission from Wang et al. (16). To see this figure in color, go online.