Full-length p53 Tetramer Bound to DNA and Its Quaternary Dynamics

Abstract

p53 is a major tumor suppressor that is mutated and inactivated in about 50% of all human cancers. Thus, reactivation of mutant p53 using small-molecules has been a long sought-after anti-cancer therapeutic strategy. Full structural characterization of the full-length oligomeric p53 is challenging because of its complex architecture and multiple highly flexible regions. To explore p53 structural dynamics, here we developed a series of atomistic integrative models with available crystal structures of the full-length p53 (fl-p53) tetramer bound to three different DNA sequences: a p21 response element, a puma response element, and a non-specific DNA sequence. Explicitly solvated, all-atom molecular dynamics simulations of the three complexes (totaling nearly 1 μs of aggregate simulation time) yield final structures consistent with electron microscopy maps and, for the first time, show the direct interactions of the p53 C-terminal with DNA. Through a collective principal component analysis, we identify sequence-dependent differential quaternary binding modes of the p53 tetramer interfacing with DNA. Additionally, L1 loop dynamics of fl-p53 in the presence of DNA is revealed, and druggable pockets of p53 are identified via solvent mapping in order to aid future drug-discovery studies.

p53, also known as “the guardian of the genome”, lies at the heart of the tumor-suppression mechanism against mutations occuring daily in the human DNA. Once activated, p53 signals for cell-cycle arrest, senescence, or apoptosis, either via transcription of various target genes ^{1, 2} or through non-transcriptional pathways ^{3, 4, 5}. As tumor initiation and maintenance requires the inactivation of p53 pathways, it is also the most frequently mutated gene in human cancers. Thus, many researchers seek small molecules that can reactivate mutant p53 ^{6, 7, 8, 9, 10, 11}. Recent research in transgenic mice demonstrated that p53 reactivation can indeed achieve tumor regression, highlighting p53 reactivation as a very promising anti-cancer therapeutic strategy ^{12, 13, 14}.

Full-length p53 (fl-p53) is in part an intrinsically disordered protein (IDP) and binds DNA as a tetramer ¹⁵. Due to high flexibility, IDPs rarely form crystals and often yield complex NMR spectra ¹⁶. Fl-p53 consists of 393 residues that form a flexible N-terminal domain (NTD), a core DNA binding domain (DBD), a flexible linker region, a tetramerization (TET) domain, and a flexible C-terminal domain (CTD) ¹⁷ (Fig. 1a). The core p53 DBD domain is the most studied because all inactivating p53 mutations occur there, and it has definite secondary and tertiary structural elements allowing structural characterization. However, the detailed DNA binding mechanism of p53 is not well characterized. Recently, scientists crystalized the tetrameric p53 DBD and TET (with the linker domain truncated) bound to a short strand of DNA, setting the stage for the current study ^{18, 19, 20}.

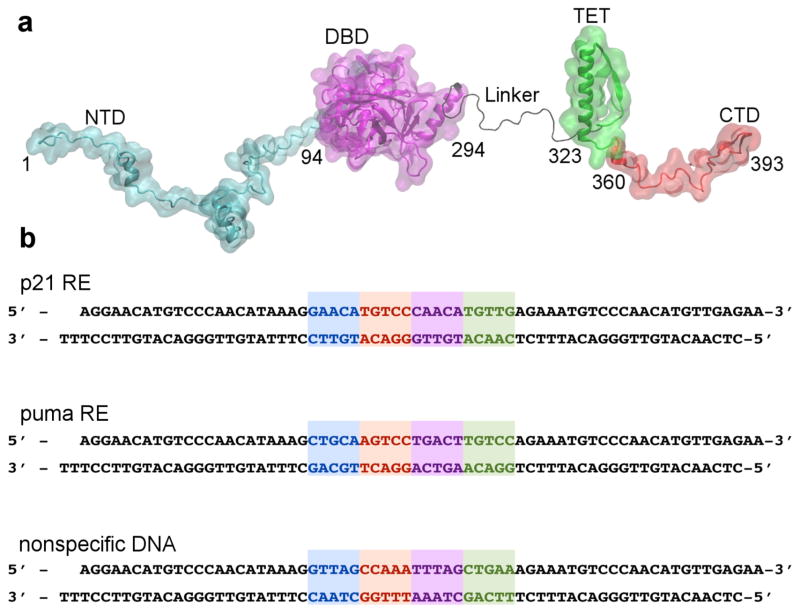
Figure 1. Full-length p53 and the different DNA set-up.

a) The full-length p53 (fl-p53) sequence with each of the five domains labeled: N-terminal domain (NTD), DNA binding domain (DBD), linker, tetrameric domain (TET), and C-terminal domain (CTD). b) The three different DNA sequences used in the simulations: the two positive response elements (REs), p21 RE and puma RE, and a non-specific DNA sequence. The binding motif consists of four pentamer repeats. Pentamers a, b, c, and d are highlighted in blue, red, purple and green, respectively.

Upon activation, p53 needs to efficiently locate and bind to its response elements (REs) on the genome in order to stimulate transcription of target genes and subsequently regulate the cell cycle by initiating DNA repair, cell-cycle arrest, or apoptosis ^{1, 2}. However, the mechanism by which p53 searches and recognizes its REs, is still under debate. REs consist of four head-to-head nucleotide pentamer repeats (RRRCWWGYYY), where R is A or G, W is A or T and Y is C or T ¹⁸ (Fig. 1b). The fl-p53 tetramer forms a dimer of dimers and each p53 monomer binds to a pentamer repeat ²¹. The fl-p53 tetramer tightly binds to the REs signaling for cell-cycle arrest (e.g. p21), while its affinity towards the pro-apoptotic REs (e.g. puma) can be either high or low ²².

The role of the CTD in facilitating p53’s DNA search has been controversial ²³. Earlier studies showed that the p53 CTD acts as a negative regulator by hindering DBD binding to the short strands of specific response elements (REs) ²⁴. However, further research suggested the opposite: the p53 CTD is needed for the DBD to recognize target sites in long or circular DNA and acts as a positive regulator ²⁵. Tafvizi et al. explained these two seemingly contradictory observations by proposing a search and a recognition binding mode, in which CTDs facilitate target-site search by sliding through the non-specific DNA while the DBDs are immobilized, moving by frequent association and dissociation ²⁶.

Lastly, the p53 L1 loop is implicated to be an important conformational switch that regulates DNA binding ^{19, 20}. The crystal structure of a recent p21-RE-bound tetrameric p53 showed that the L1 loop can adopt either an extended or recessed conformation ¹⁸. Lukman et al. performed molecular dynamics (MD) simulations of a p53 DBD monomer in the absence of DNA ²⁷. They observed that the L1 loop was the most flexible region in DBD, and can adopt both an extended and a recessed conformation, switching from one conformation to another on the nanosecond timescale ²⁷. The L1 loop also forms part of the druggable L1/S3 pocket that docks a p53-reactivating molecule ⁶. To address the structural dynamics and molecular recognition of the fl-p53, we constructed all-atom fl-p53 tetramer models bound to 3 DNAs, including two REs and a non-specific DNA, and explored their dynamics via explicitly solvated molecular dynamics (MD) simulations (Fig. 1b).

Results

Comparison of the MD simulations to the EM map

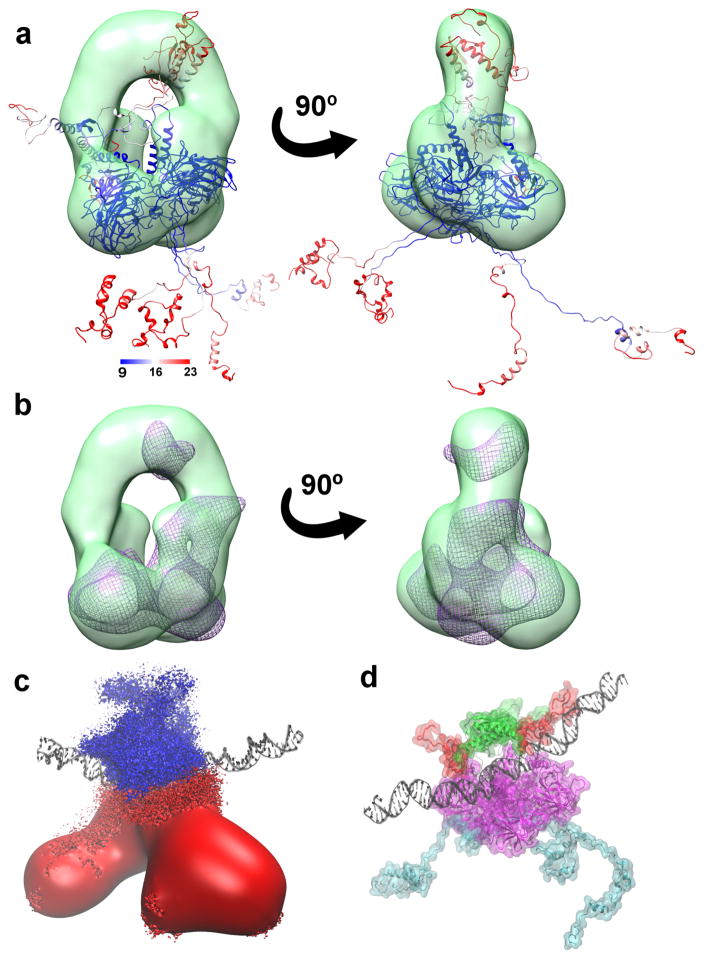
The RMSF values of the fl-p53 calculated from all the simulations combined showed that NTDs and CTDs were the most flexible, consistent with the prior electron microscopy data ²⁸. Melero et al. reported that no density of the flexible N-terminal and the C-terminal regions was found in the EM maps ²⁸. A representative cluster centroid of fl-p53 tetramer colored by the RMSF values could be fitted into the EM map, with the flexible regions mostly outside and the rigid domains inside the map (Fig 2a). Furthermore, we calculated a density map collected from the simulations and fitted it into the EM map (Fig 2b) with a correlation coefficient of 0.84.

Figure 2. Full-length p53 global conformational change.

a) A representative fl-p53 structure colored based on RMSF values and fitted into the class III EM map (depicted in green surface representation) from Melero et al²⁸ b) The simulated density map depicted as a purple wireframe surface fitted into the same EM map in panel a. c) Ensemble-averaged electrostatics map for fl-p53 tetramer. Negative electrostatic isosurface drawn at -4 kT/e is colored in red and positive electrostatic isosurface drawn at +4 kT/e is shown in blue. DNA is depicted as black ribbons for reference. d) The p53 C-terminals, highlighted in red, interacting with the DNA, depicted as black ribbons. NTD, linkers, DBD and TET were colored in cyan, black, magenta, and green, respectively.

Steady decrease of the radius of gyration

In order to monitor the global changes in the p53 tetramer, we calculated the radius of gyration values of the simulations. Radius of gyration reflects how far the protein stretches from its center of mass, and thus, a small radius of gyration indicates a more compact structure, while a large radius of gyration indicates a more elongated one. Our initial model had all flexible loops in extended conformation, and the radius of gyration decreased steadily during simulations in all systems. However, among the 3 systems with different DNA sequences, the non-specific DNA-bound system reached the lowest radius of gyration at the end of the simulations while the p21-RE-bound system reached the largest value (Supplementary Fig. 1). Our results indicated that the fl-p53 tetramer adopts the most compact form when bound to a non-specific DNA sequence, and the most elongated form when bound to the p21 RE. The fl-p53 tetramer interacting with the puma RE fell in the middle.

C-terminal domain directly contacts the DNA

The flexible C-terminal loops significantly contributed to the steady decrease radius of gyration. Moreover, ensemble-averaged electrostatics of the fl-p53 tetramer showed that the C-terminals carry a positive potential, favorable for interacting with the negatively-charged DNA backbone (Fig. 2c). Visualization of the MD trajectories revealed that the C-terminal domains of the fl-p53 tetramer approached and directly contacted the DNA in all of our simulations independent of the DNA sequence (Fig. 2d and Supplementary Fig. 1). This is a remarkable observation in 110 ns simulations given that the C-terminal domains had very extended conformations and were quite distant from the DNA initially. Especially the C-terminal of monomer C ended up contacting the DNA in every single MD simulation. In our initial model system, the C-terminal of monomer C was unintentionally built slightly closer to the DNA. Yet, the C-terminals of other monomers including monomers A and B also ended up interacting directly with the DNA.

We also performed a principal component analysis (PCA) including all fl-p53 Cαs in all simulations. The first principal component (PC1) was a motion of the CTDs becoming more compact and approaching the DNA, in line with the steady decrease of the radius of gyration (Movie S1). All three systems sampled the motion described by PC1.

Lastly, we carried out an interaction footprint analysis and identified the salt bridges between the p53 CTDs and DNA (Supplementary Table. 1). The key p53 residues that participated in the salt bridge interactions were Lys370, Lys372, Lys373, Arg379, Lys381, Lys382 and Lys386. The p53 CTDs interacted with the DNA only non-specifically via the DNA backbone atoms, and the interactions were dynamic with different parts of the DNA segments interacting at different times. The motions we observed at the molecular level directly supported the previously suggested idea that p53 CTDs do not participate in specific DNA recognition and binding, but rather participate in dynamic DNA search ²⁶.

Quaternary binding modes of p53 DBD tetramer to different DNA sequences

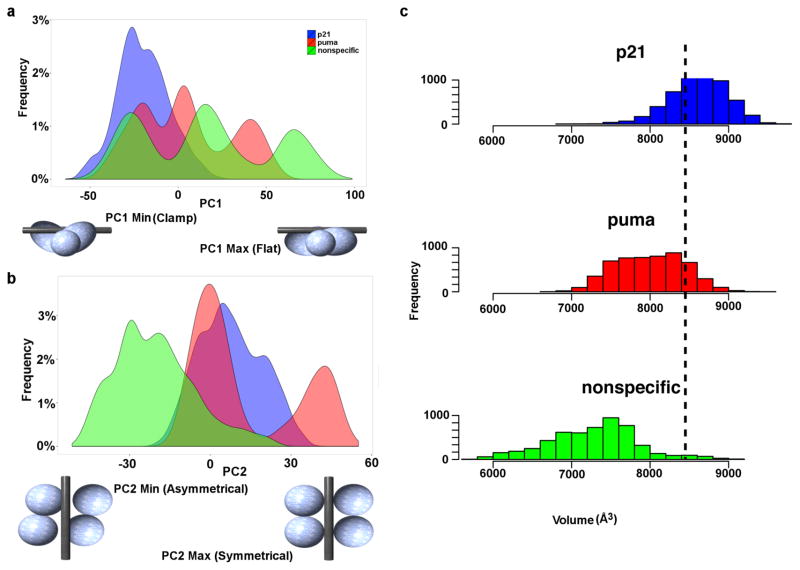
Besides the PCA on all the Cα atoms of fl-p53, we performed another PCA including only the Cα atoms of the DBDs (residues 89–291) of the p53 tetramer. Interestingly, in this case, PC1 showed a clamping/unclamping motion of the tetrameric p53 DBDs around DNA. This quaternary motion can be described in more detail as going from a more asymmetric form of the p53 DBD tetramer clamped around the DNA with 2 DBDs curved inward (low PC1 values) to a more symmetric and flat form of the p53 DBDs in which all 4 monomers are in plane (high PC1 values) (Fig. 3a and Supplementary Movie 2). In our simulations, the p21 RE system only sampled low PC1 values while the puma RE and the non-specific DNA systems extended beyond and sampled both low and high PC1 values (Fig. 3a). In other words, the p21 RE system sampled only the more clamped configuration while the puma RE and non-specific DNA systems sampled both the clamped and the flat configurations. The puma RE system spent more time sampling the more clamped configuration and less time in the flat configuration while it was vice versa in the non-specific DNA system (Fig. 3a). We should also note that all these model systems were constructed by mutating the DNA in the crystal structure of the p21-bound p53 tetramer system and thus the initial configuration was the same for all of them. The fl-p53 tetramer is known to have much higher binding affinity to the p21 RE compared to the puma RE, and a minimal binding is expected in the case of the non-specific DNA sequence. PC1 indicated that the fl-p53 tetramer adopts different DBD tetramer configurations to accommodate tighter DNA binding as in p21 RE, weak DNA binding as in puma RE, and minimal binding as in non-specific DNA.

Figure 3. Quaternary DBD binding modes.

Histograms showing the a) PC1 and b) PC2 distributions of each system. p21, puma, and the nonspecific DNA system distributions are colored in blue, red and green, respectively. The binding modes corresponding to the minimum and maximum values of PC1 and PC2 are drawn in cartoon underneath each x-axis. c) Histogram showing the distribution of the grab volume between the four DBDs during simulations of each system. The black dashed line demonstrates the initial grab volume value prior to the simulations.

On the other hand, PC2 described a cooperative binding motion of the p53 DBD tetramer upon specific DNA recognition. This quaternary motion can be described in more detail as going from an asymmetric non-cooperative mode, in which monomers A and D are pushed away from the DNA (low PC2 values), to a symmetric cooperative binding mode, in which all four monomers are in close proximity to DNA (high PC2 values) (Fig. 3b and Supplementary Movie. 3). In our simulations, both the p21-RE-bound and puma-RE-bound p53 tetramer systems sampled only high PC2 values while the non-specific DNA-bound p53 tetramer system solely sampled low PC2 values (Fig. 3b). We should again note that all of our MD simulations started from a cooperative binding mode observed in the p21-RE-bound p53 tetramer crystal structure.

To further inspect the effect of different quaternary binding modes of the p53 tetramer on the DNA binding interface, we measured the “grab volume” as a metric that quantitates the space available between four p53 DBD monomers that is open for binding and accommodation of DNA. The results from our simulations revealed that the p21-RE-bound system provided the largest grab volume to accommodate DNA followed by puma-RE-bound and then non-specific DNA-bound systems (Fig. 3c). The binding mode seen in p21-RE-bound simulations (characterized by low PC1 and high PC2 values) provided the largest grab volume for DNA accommodation, while the binding mode seen in non-specific DNA-bound simulations (characterized by high PC1 and low PC2 values) provided the smallest grab volume.

Furthermore, hydrogen-bond footprint analysis complemented our DBD PCA analysis (Supplementary Table 2). There were 10 direct hydrogen bonds we identified between fl-p53 DBDs and DNA, but here we focused on the most significant ones. The two most persistent H-bonds we observed in MD were the hydrogen bond between the Ala276 backbone and DNA, and the hydrogen bond between the Arg280 side chain and DNA. These two H-bonds were observed highly persistently only in the case of the positive REs, p21 and puma, but were very scarcely seen in the case of the non-specific DNA system. The Arg273 side chain also formed a more persistent H-bond to DNA in the p21 RE and puma RE systems compared to the non-specific DNA system, but the difference was less pronounced. Ser241 was the only residue that interacted with all three DNA sequences persistently, indicating that Ser241 is a sequence-independent H-bond donor/acceptor for DNA. This persistence of this hydrogen bond interaction across all DNA segments suggests that Ser241 may play a key role in the DNA search process. We should also note that the most persistent H-bond between Lys120 and DNA was seen only in the inner monomers (monomers B and C) of the p21 RE system and the puma RE system, less persistent in the latter. The H-bond between Lys120 and DNA was not persistent in the non-specific DNA system. Overall, more persistent H-bonds between the fl-p53 tetramer and DNA were observed in the p21 RE and puma RE systems compared to the non-specific DNA-bound system, in line with the clamped binding modes observed for the positive RE systems.

In this study, p53 DBD tetramers were explicitly shown to adopt different configurations upon binding to various DNA sequences. We observed that the p53 DBD tetramer adopts a cooperative, clamping, tight-binding mode to bind positive REs (e.g., p21 and puma) while it adopts a non-cooperative, flat, loose-binding mode to bind non-specific DNA sequences (Fig. 2a,b). These two binding modes can be related to the two-state mechanism of DNA search and recognition suggested for p53 by Tafvizi et al. based on their single-molecule experiments ²⁶. The non-cooperative, loose-binding mode we observed in the non-specific DNA case can represent the DNA search mode of the fl-p53 tetramer, while the cooperative, tight-binding mode in the p21 RE case can represent the DNA recognition mode.

DNA Distortion

Next, we examined the effects of the fl-p53 tetramer binding on the structure of the DNA. It has been shown previously that DNA bends by 27° upon binding to the fl-p53 tetramer ^{29, 30, 31}. Among our three systems, we observed that only the p21-RE-bound p53 tetramer system achieved significant DNA bending and agreed well with the experimental value (Supplementary Fig. 2).

Beyond DNA bending, further examination of the average DNA properties in our simulations revealed several sequence-dependent features. (Table 1) The minor groove width was 7.28Å ± 1.12Å, 7.78Å ± 1.13Å and 4.79Å ± 1.20Å for the p21 RE, puma RE, and non-specific DNA systems, respectively. The minor groove width for B-DNA is typically 4.2 Å ± 1.29Å ³², which is within the standard deviation of the non-specific DNA minor groove width, but significantly lower than the values observed in the positive REs. In fact, the typical value for A-DNA minor groove width is 9.70 ± 0.17Å, which is a closer value to the two values calculated for the positive REs. The much wider DNA minor grooves observed in p21-RE and puma-RE-bound fl-p53 tetramer systems suggest that the minor groove widens when the fl-p53 tetramer binds these positive REs in a DNA recognition mode.

Table 1. Comparison of average DNA properties in MD simulations of the three systems.

Average and standard deviation of the values in 3 copies of MD simulations are reported.

	p21	puma	non-specific DNA
Minor groove width	7.28 ± 1.12 Å	7.78 ± 1.13 Å	4.79 ± 1.20 Å
h-twist	29.2 ± 5.7°	30.4 ± 7.4°	34.0 ± 4.1°

Another DNA property we found to be sequence-dependent was the h-twist, which corresponds to the rotation between base pairs ³². The h-twist in our simulations were 29.2° ± 5.7°, 30.4° ± 7.4°, and 34.0° ± 4.1° for p21 RE, puma RE and non-specific DNA systems, respectively (Table 1). The two smaller values observed in the two positive REs, p21 and puma, suggested that in the DNA recognition mode, p53 binding caused a slight DNA untwisting.

L1 loop dynamics

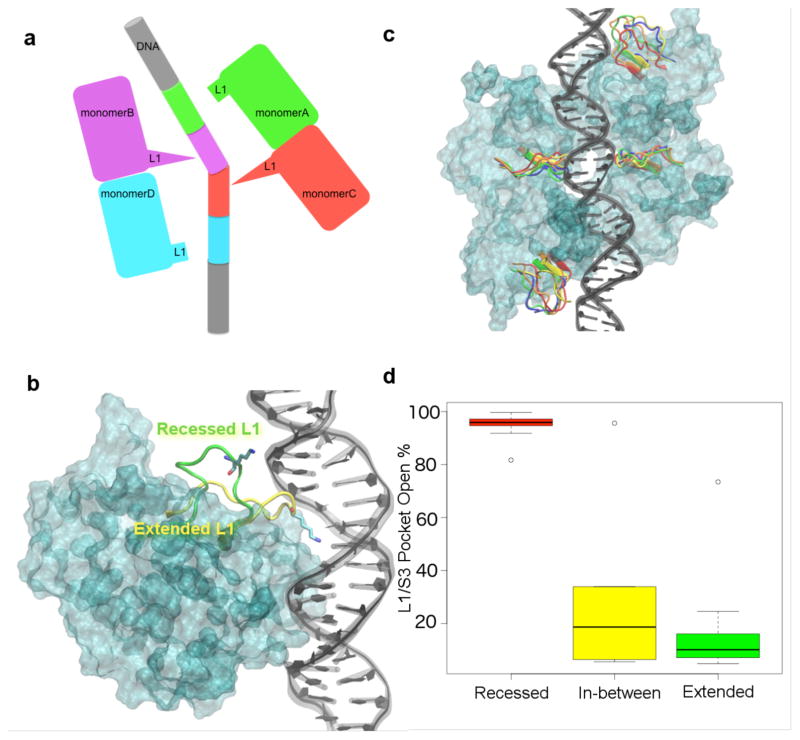
In the crystal structure of the tetrameric DBD binding to DNA, the L1 loops from the outer two monomers (monomers A and D) adopt a recessed conformation and the L1 loops from the inner two monomers (monomers B and C) adopt an extended conformation (Fig. 4a,b) ¹⁸. To monitor the L1 loop dynamics of each p53 monomer in our simulations, we measured the time-dependent RMSD of the L1 loop Cα atoms with respect to these two conformations in the crystal structure. We did not observe a complete transition of the L1 loop from recessed conformation to extended conformation or vice versa in any of the simulations. The L1 loops of the inner p53 monomers conserved the extended L1 loop conformation throughout the simulations independent of the DNA sequence (Fig. 4c and Supplementary Fig. 3–5). However, the recessed L1 loops of the outer p53 monomers were more flexible and sampled intermediate conformations in addition to the recessed conformation (Fig. 4c and Supplementary Fig. 3–5). These intermediate L1 conformations were sampled by at least one monomer in the p21 RE and non-specific DNA systems, while it was not observed in the puma RE system (Supplementary Fig. 3–5). Based on our simulations, the L1 loop conformation of a p53 monomer in DNA-bound fl-p53 tetramer system is dictated by the position of the monomer with respect to the DNA (Supplementary Fig. 6).

Figure 4. L1 loop conformations in the fl-p53 tetramer.

a) Cartoon figure depicting the two different L1 conformations in DNA-bound p53 tetramer crystal structure. The extended L1 loops are seen in monomers B and C while the recessed L1 loops are seen in monomers A and D. b) Extended L1 conformation (shown in yellow ribbons) of a p53 monomer (cyan surface) interacting with the DNA (depicted in black). Recessed L1 loop conformation from another superimposed monomer is also shown in green ribbons for comparison. Lys120 on each L1 loop is drawn in sticks. c) The conformational space the L1 loop can sample in each monomer. The L1 loops in the most-populated 5 conformations are colored in red, orange, yellow, green and blue. The DBD monomer surfaces are colored in cyan and the DNA is colored in black. d) Boxplot that shows the median, 1^st and 3^rd quantiles, and the outliers of the time percentage of the L1/S3 pocket being open at various L1 conformations.

We were interested in the L1 dynamics also because it directly effects the druggable L1/S3 pocket we previously identified ⁶ near the L1 loop and found strong evidence to be the binding site for PRIMA-1 in clinical trials ⁸. In the same study, we also discovered stictic acid to be a novel p53 reactivation compound by using the MD-generated L1/S3 pocket-open conformation in virtual screening ⁶. Using several geometric criteria as a filter for the pocket-open state, we found the L1/S3 pocket was open only about 6% of the time in 30 ns MD simulations of the DBD monomers of wild-type p53 and various p53 mutants ⁶. In order to investigate the L1/S3 pocket dynamics in fl-p53 tetramer systems, we calculated the percent time the L1/S3 pockets were open in MD simulations using the same geometric criteria established in Ref. ⁶. In the L1 loops with an initial extended conformation (monomers B and C), we found that the L1/S3 pocket was open only 7% to 15% of the time with only one exception. (Fig. 4d and Supplementary Table 3) On the other hand, we found that in most of the L1 loops with an initial recessed conformation (monomers A and D), the L1/S3 pocket was open 80% to 99% of the simulation time. (Fig. 4d and Supplementary Table 3) Much lower L1/S3 pocket-open percentages were computed only for the monomers A and D whose L1 loops spent a significant amount of time sampling the intermediate conformations. (Fig. 4d and Supplementary Table 3) Overall, we found that a recessed L1 loop conformation in the DNA-bound fl-p53 tetramer correlated with a mostly open L1/S3 pocket, while an extended L1 loop conformation correlated with a rarely open L1/S3 pocket. (Fig. 4d and Supplementary Table S3)

FTMAP provides insight into druggable pockets found in fl-p53

Besides the L1/S3 pocket, we were also interested in locating novel cryptic druggable sites in fl-p53. The solvent-mapping results from FTMAP identified multiple druggable sites in the DBD as well as in the transactivation (TAD) and the tetramerization (TET) domains. Consensus druggable sites in the TAD and TET domains were not consistently identified, presumably due to the high flexibility of these two regions. In contrast, the druggable sites on the DBD surface were consistent among all systems and all monomers. The DBD druggable sites we identified on the p53 DBD are the L1/S3 pocket, the L1 back pocket, the Tyr220 pocket, the Met160 pocket and the Gln192 pocket (Supplementary Fig. 7). The previously identified druggable L1/S3 pocket may develop further, by molecules that tunnel through the L1 back pocket. The Tyr220 pocket consisted of two pockets with a loop in between them, and was recently shown to bind a ligand that can exploit one of the Tyr220 pockets as well as the transient tunnel between the two pockets¹¹. The Tyr220 pockets in monomers B and C (the inner monomers) were at the interface of two monomers and may not be easily accessible. The Gln192 pocket predicted by FTMAP falls between the DBD and the NTD of p53. Thus, this druggable pocket would not reveal itself if we had included only the p53 DBDs in our simulations. Further studies are required to validate these predicted druggable pockets experimentally.

Discussion

We report here several integrative all-atom models of the full-length p53 tetramer bound to different DNA sequences and their respective dynamics via MD simulations that total nearly 1 μs of sampling. The resulting fl-p53 ensembles from our simulations agree and fit well into the previously determined EM maps ²⁸. (Fig. 2a,b) The best correlation value we obtained was R=0.84 between our ensemble-averaged density map of the p21-RE-bound system and the class III EM map. The closest all-atom model to a full-length p53 tetramer generated in a very recent study included only the residues between 91 and 359 lacking the NTD and CTD regions and was only simulated for approximately 100 ns in total ³³. In our longer and more structurally comprehensive simulations, the TET domains moved about 40 Å toward the DBD center of mass, and the extended CTDs became more compact and approached the DNA, while the NTDs remained mostly in extended form and very dynamic throughout simulations. The ensemble-averaged electrostatic maps of the fl-p53 showed that the TET and DBD were generally positive and the NTD was negative (Fig. 3c). This helps explain why the CTDs moved towards the DNA, while the NTDs did not, despite being highly flexible.

In every single simulation we performed, the CTDs of the p53 monomers ended up approaching and directly interacting with the DNA phosphates non-specifically via the positively charged residues including Lys372, Lys373, Lys381 and Lys382, which were also implicated to have a role in DNA binding in previous experimental studies ^{34, 35}. Arlt et al. showed the p53 CTDs to be very flexible by chemical cross-linking followed by mass spectroscopy ³⁴. They also found CTD Lys381 is capable of cross-linking with TET domain Lys357, suggesting that CTD is in close proximity to the TET domain ³⁴. Their experimental data is in line with our observations. Furthermore, Friedler et al. showed that acetylation at each of these CTD residues would weaken DNA binding ³⁵. Acetylation neutralizes the positively-charged CTD residues hindering the interaction with the negatively-charged DNA backbone. Our simulations explicitly demonstrated at the molecular level that CTDs directly interact with the DNA via non-specific electrostatic interactions and thus, the interactions are very dynamic.

Through virtual mutations of the initial DNA structure, we also integrated three different DNA sequences, namely p21 RE, puma RE and non-specific DNA, into the fl-p53 tetramer model in order to search for different quaternary DNA binding modes. p53 tetramer is known to bind tightly to the p21 RE (K_D=4.9 nM) which signals for cell-cycle arrest, and slightly weakly to the puma RE (K_D=7.1 nM) ²² which signals for apoptosis ²². Integrating a non-specific DNA sequence into our model, we wanted to explore whether there is a non-specific DNA binding mode of fl-p53 similar to the case of BamHI, for which crystal structure of a unique and loose binding mode to a non-specific DNA was captured ³⁶. Under physiological conditions, K_D values of fl-p53 for known REs are an order of magnitude lower than the K_D values of non-specific DNAs ³¹. In line with this, the persistent contacts observed between fl-p53 tetramer and positive REs in simulations were significantly weaker in the case of non-specific DNA simulations.

Using single-molecule imaging tools, the diffusive motion of individual p53 proteins was recently monitored and quantitatively characterized²⁶. Comparing the diffusive motions of different p53 constructs (namely fl-p53, NTD+DBD+TET and TET+CTD), they revealed that p53 TET+CTD construct can translocate on DNA much faster than fl-p53, while NTD+DBD+TET construct remains immobile due to the absence of CTD ²⁶. Based on these single molecule experiments, a two-state search mechanism was proposed for p53 search on DNA: a search state with mostly nonspecific binding and fast sliding, and an immobile recognition state with sequence-specific binding ^{26, 37}. In the search state, the CTDs accelerate the p53 sliding motion on DNA. And in the recognition state, the p53 DBD binds tightly and sliding is minimal ²⁶. Through principal component analysis (PCA) of p53 DBD tetramer dynamics from MD simulations of all three systems, we identified differential binding modes depending on the DNA sequence. The clamped, symmetrical, cooperative mode uniquely sampled by the p53 DBDs binding to p21 RE can represent the recognition state while the flat, asymmetrical, non-cooperative mode sampled mostly by the DBD binding to non-specific DNA sequence can represent the search state. Including both the positive REs and non-specific DNA sequence in our various simulations and performing a collective PCA, we were able to capture a conformational change motion that is indicative of multiple DNA binding modes of fl-p53, even though the timescales of our MD simulations are probably not long enough to observe the entire event in a single simulation.

We also analyzed the conformation and dynamics of the p53 L1 loop that directly interacts with DNA and forms part of the druggable L1/S3 pocket. The first crystal structure of a p53 tetramer bound to a natural RE (pdbID: 3TS8) showed that L1 loops have adopted an extended conformation in the two inner monomers (monomers B and C) and a recessed conformation in the two outer monomers (monomers A and D) ¹⁸. Prior to 2011, all p53 L1 loops in the crystal structures were found in extended conformation. Lukman et al ²⁷ performed multi-copy 100 ns simulations of a single p53 monomer DBD (without any DNA bound) and observed that the L1 loop samples both the extended and recessed conformations regardless of the starting conformation of the L1 loop. In our 110 ns simulations of the DNA-bound full-length p53 tetramer, we did not observe any full transitions of a recessed L1 loop into an extended L1 loop or vice versa. Especially, the extended L1 loop conformations were persistent in inner monomers B and C of all the simulations. Nevertheless, we have observed flexibility in both conformations with a significantly greater mobility in the recessed L1 loop conformation as shown in Fig. 4c. When one of the inner p53 monomers with an extended L1 loop conformation is superimposed onto an outer p53 monomer with a recessed L1 loop conformation in the crystal structure, there is a clear steric clash between the DNA and the extended L1 loop (Supplementary Fig. 6). Thus, the outer p53 monomer can’t adopt an extended L1 loop conformation when fl-p53 tetramer binds tightly to DNA. Our data and previous data from Lukman et al.²⁷ together indicate a conformational selection for the p53 tetramer L1 loops upon DNA binding, dictated by the position of the monomer with respect to DNA. In the inner monomers, L1 loop adopts an extended conformation due to favorable DNA interactions, while in the outer monomers, L1 loop can not sample extended conformation due to steric clash, but samples the recessed conformation as well as some intermediate ones.

The correlation between the L1 loop dynamics and the behavior of the druggable L1/S3 pocket in the DNA-bound fl-p53 tetramer system suggests that the presence of DNA affects the pocket dynamics. Supplementary Table 3 shows that the L1/S3 pocket is open at least 80% of the time on the two outer monomers, in which L1 loops adopt the recessed conformation. Whereas, the L1/S3 pocket is found open less than 15% of the time on the inner monomers, in which L1 loops strictly stick to the extended conformation. Based on our data, the L1 loop conformations are constrained by DNA binding, and profoundly alter the L1/S3 pocket open percentage. We should also note that the L1/S3 pocket open percentages in this study are much higher compared to the previous values found in single p53 DBD monomer simulations of Wassman et al. ⁶ despite using the exact same set of criteria to define an open pocket. In these previous simulations, the L1/S3 pocket was found to remain open less than 10% of the simulation time ⁶. The difference between the two results could be explained by the effect of DNA binding as well as the inclusion of fl-p53 tetramer instead of a single p53 DBD monomer.

Materials and Methods

Model Construction

Fl-p53 consists of 393 residues. As the main scaffold, we used the tetrameric p53 crystal structure pdbID:3TS8 ¹⁸, which is bound to a p21 RE. The crystal structure had 18 mutations, which were mutated back to their native amino acids to build the wild-type model. This structure includes both the catalytic DBD (residues 94–291) and the TET domain (residues 321–356), but lacks a flexible-linker region (residues 291–321) ¹⁸. The missing NTD, CTD and flexible linker region is inserted via molecular modeling and using previous partial crystal structures. The double-stranded DNA (dsDNA) sequence in the crystal structure ¹⁸ which corresponds to p21 5’ site ²² was extended on both sides to obtain a 65-nucleotide dsDNA (Fig. 1b).

We modeled the missing linker region using MOE ³⁸ and VMD ³⁹, based on chain A, residues 176–199, of pdbID:1MT6 ⁴⁰, which the Schrodinger suite identified as having the highest sequence similarity to the linker region in a BLAST search ⁴¹. We also modeled residues 91–94 using the crystal structure pdbID:2XWR ⁴². These residues have recently been identified as components of the core domain.

For each monomer, the N-terminal domain was modeled by superimposing residue 35 of crystal structures pdbID:2K8F ⁴³ (chain B, residues 1–35) and pdbID:2B3G ⁴⁴ (chain B, residues 35–56), and then connecting the two complexes. Within residues 59–91, residues 66–86 are known to adopt a poly-proline-II (PPII) structure, so we modeled that region appropriately while using an extended conformation for the remainder of the flexible linker. After modeling the four flexible N-terminal domains and integrating these into the tetrameric p53 model, relative conformations of the N-terminal domains were adjusted by optimizing dihedral angles to prevent steric clashes, using MOE.

For each monomer, the C-terminal domain was modeled by connecting the non-alpha-helical parts of pdbID:1DT7 ⁴⁵ (residues 367–378) and pdbID:1H26 ⁴⁶ (residues 378–386). The missing residues 356–367 and 386–393 are modeled in an extended conformation using MOE and integrated with VMD ³⁹. After modeling the four flexible CTDs, relative conformations of these were again adjusted by optimizing the dihedral angles using MOE.

To explore the effect of binding to different DNA sequences, we modified the DNA sequence manually to a puma RE sequence (a.k.a. puma BS2) ²², as seen in Figure 1b. Furthermore, in an attempt to capture the loose p53-DNA binding mode, we used a DNA sequence comprised of the most unlikely nucleotide at each RE position. We obtained this non-specific DNA sequence based on a sequence logo that depicts the frequency of each nucleotide to be at each of the 20 positions of the RE as a result of analyzing 100 known p53 REs ⁴⁷ (Fig. 1b).

Once the systems were built, Na⁺ ions were added to neutralize each system. In addition to conserving all crystallographic water molecules, a 12 Å TIP3P ⁴⁸ water buffer was used to solvate the system explicitly, using the Amber12 suite ⁴⁹. Zinc and its coordinating residues were modeled using the cationic dummy atom model ⁵⁰. Each system consisted of 1,592,100 atoms and was built using the Amber FF14SB force field ⁵¹.

Molecular Dynamics Simulations

Energy minimization was first performed on the p21 RE, puma RE, and non-specific DNA systems. Each system was restrained, and atom positions were gradually relaxed to allow atomic fluctuations. System relaxation was performed gradually in five steps. In the first 2,000 steps, we constrained all non-hydrogen atoms. In the second 2,000 steps, we constrained the zinc ions, protein, DNA, and non-hydrogen atoms while letting the hydrogen atoms, water molecules, and ions move freely. In the third 2,000 steps, we constrained the zinc ions, protein, and DNA heavy atoms, but set the hydrogen atoms, water molecules, ions, and the zinc-coordinating residues free. During the fourth 10,000 steps, only the protein and DNA backbone were constrained. During the final 20,000 steps, all atoms were set free. The non-bonded energy was calculated at every step. Long-range interactions were calculated using the Particle Mesh Ewald method with a cut-off distance of 10 Å ⁵². At 8 Å, a switching function was applied to improve energy conservation.

After minimizations, equilibrations were performed on the three systems. Throughout the equilibration, we held the water bonds rigid while slowly decreasing the harmonic constraints on the heavy atoms in 0.25-nanosecond (ns) increments that ultimately totaled 1 ns. Following the equilibrations, an NPT ensemble was performed with no positional constraints. Langevin dynamics kept the temperature constant at 310 K with a gamma value of 5 picoseconds/terahertz. A Langevin piston barostat held the pressure constant at 1 atm with an oscillation period of 100 femtosecond (fs) and a damping time scale of 50 fs.

Three independent MD simulations were performed for each of the three systems at 310 K and 1 atm using NAMD2.10 program ⁵³. Each MD copy for p21 RE system was 109 ns, and each MD copy for puma RE and nonspecific DNA systems were 110 ns. In total, we simulated almost 1 μs of DNA-bound fl-p53

Radius of Gyration

The radius of gyration was calculated using cpptraj, a component of the Amber suite ⁴⁹. The average radii of gyration with respect to time were calculated for two regions: the fl-p53 Cα atoms and the Cα atoms of the DBD and TET. The results were then plotted using the ggplot2 package ⁵⁴ in R.

Principle Component Analysis

Our PCA analysis followed these steps. 1) We concatenated and aligned all the trajectories using the α-carbons of residues 89 to 291 for the DBD PCA analysis, and all α-carbons for the alpha-carbon PCA analysis. 2) We created a covariance matrix using the α-carbons of the residues of interest. 3) We diagonalized the co-variant matrix to obtain the eigenvectors and the corresponding eigenvalues. 4) We projected the trajectories onto the first and second eigenvectors. 5) We generated pseudo trajectories from the first and second eigenvector to study the motion decomposed by each principal component. The above steps were performed using cpptraj⁴⁹. The resulting projections were plotted using gnuplot ⁵⁵.

Salt-Bridge Formation

The positive residues of the fl-p53 and the negative DNA phosphate backbone often formed salt bridges. To inspect these salt bridges, we first generated a list of fl-p53 Lys and Arg residues that were positioned within 5 Å of DNA, using a tool command language (tcl) script executed in VMD. We then loaded the trajectories into VMD and visually identified salt bridges between the DNA and the selected Arg/Lys residues. To quantify the analysis of the salt bridges, we manually extract the distance between the positive nitrogen atom and the negative oxygen atom and used a python script to calculated the percent bond occupancy using a distance cutoff of 3.5 Å ⁵⁶.

Volume Calculation

The grab volume between the four DBD monomers accommodate for DNA binding was calculated using POVME 2.0.⁵⁷ An inclusion sphere centered at Cartesian coordinates [128, 135, 115.5] with a radius of 17 Å fully engulfed the gap between the four monomers. A seed was planted in the center of the sphere and extended for 4 Å. POVME 2.0 calculated the volume starting from the seed and continued until it reached the boundary of the inclusion region. Volumes were calculated for every fifth simulation frame. The resulting volume distribution was plotted in the R program ⁵⁴ as a histogram.

Hydrogen-Bond Analysis

Using the VMD Hbond plugin, we generated a list of direct hydrogen bonds between the fl-p53 and various DNA sequences, using 3.5Å and 20° distance and angle cut-offs, respectively³⁹. We further condensed the list by considering only those hydrogen bonds with at least 10% occupancy. A single list was compiled by combining the data from the three copies of each system using a Kepler workflow ⁵⁸. Finally, we assigned a score to each p53 residue in the list by summing its occupancy with one or multiple DNA residues.

DNA Bending Angle and Properties Analysis

The DNA bending angle was calculated using cpptraj ⁴⁹. We manually selected phosphate atoms from nucleotides 1653, 1676, and 1697 for angle calculation. The results were plotted with the ggplot2 package in R ^{32, 54}. Additional DNA properties were analyzed using the Canal software for MD trajectories, part of the Curves+ package ³². As we were particularly interested in how the DNA conformation changed upon fl-p53 binding, we set the search sequence to the four pentamer repeats (highlighted in blue, red, purple, and green in Fig. 1b) and calculated only the DNA properties of this region.

L1 Loop Analysis

The L1 loop (residues 113 to 126) was analyzed using a tcl script in VMD³⁹. First, two monomers were extracted from the crystal structure (PDBID:3TS8 ¹⁸), containing distinct examples of the extended and recessed L1 loop, respectively. They were used as a reference for simulation trajectory alignment and subsequent L1-loop root-mean-square-deviation (RMSD) calculations. The L1 RMSD was calculated twice, with respect to the extended and recessed conformations in the crystal structure, respectively. The atom selections for the alignment and the RMSD calculations were different. The trajectory alignment was performed using the DBD Cα atoms, and the RMSD calculations were performed using the L1 loop Cα atoms. The results were plotted using gnuplot ⁵⁵. Over the course of the simulations, the L1 loop was said to have adopted the recessed or the extended conformation if the extended and recessed RMSD values did not show overlap. (Supplementary Fig. 3–5) If the two RMSD values overlapped for more than 20 ns, the L1 loop was said to have adopted an intermediate structure. Furthermore, we were interested in visualizing the conformational space that the L1 loop sampled. To this end, we used cpptraj to perform RMSD clustering using a hierarchical agglomerative (bottom-up) approach ⁴⁹. We generated five clusters and extracted the centroid frame using VMD ³⁹.

C124 Pocket Analysis and Pocket Prediction

Using the distance and angle criteria of Wassman et al. ⁶, we calculated the open C124 pocket percentage with respect to time. There are two main steps in this process: input generation and the actual calculation. We first used cpptraj ⁴⁹ to generate the four distances and one dihedral angle that serve as inputs for the calculation. We then wrote a python script to pinpoint the frames that satisfy these distance and angle criteria, from which the L1/S3 pocket opening percentage was calculated. The results were plotted using basic plotting in R ⁵⁹. To identify druggable pockets in the p53 protein, we submitted the fl-p53 monomers from the final frames of the simulations to the FTMap web server ⁶⁰. FTMAP server floods protein surfaces with various small solvent molecules to find druggable hot spots ⁶⁰. We then loaded the collective results into VMD and aligned them to the whole fl-p53 system in order to locate each predicted druggable pocket.

RMSF and fitting the Density Map Generated from MD Trajectories into the p53 EM Maps

Root-mean-square-fluctation (RMSF) was calculated using cpptraj ⁴⁹. The trajectories form the three systems were concatenated and the second half (55ns to 110ns) of the simulations was used to calculate the RMSF of individual residues. We did not include the first half of the simulations because the RMSF may be biased from the initial model construct. Then, we clustered the second half of simulations and picked the first cluster centroid as the representative structure to color by RMSF values. The lowest to highest RMSF values were colored from blue to red. Density maps of the fl-p53 without the NTD domain bound to three different DNA sequences were generated using MDFF from the second half (55 ns to 110 ns) of the trajectories ⁶¹. We excluded the NTD domains because Melero et al. did not see the NTD density in their EM map. The mdff sim function was utilized and the resolution and spacing were set to 30.0 Å and 2.2 Å, respectively, in line with the experimental data ²⁸. Chimera program is used to fit the ensemble-averaged density maps from all the systems into each of the four EM maps in Melero et al^{28, 62}. To mask out noise from the EM map, only the region that have higher values than the median density value was selected for the fitting.

Ensemble averaged electrostatic map calculation

The fl-p53 ensemble averaged electrostatic maps of the three systems were calculated with DelPhi Ensemble Electrostatics. Each ensemble was comprised of 30 ns trajectories from 80 ns to 110 ns ⁶³. The calculations were performed at zero salt concentration, and using 2.0 and 80 as the solute and solvent dielectric constants, respectively.