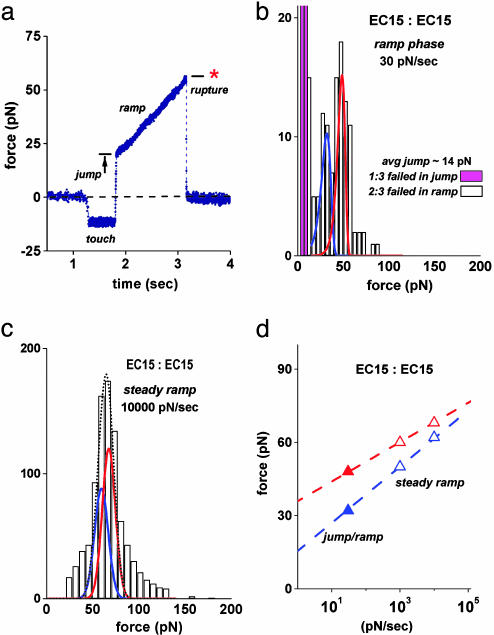
Fig. 3.
Long-lived substates of EC15 vs. EC15 interactions exposed by a jump/slow ramp force sequence and merging of these substates when tested with fast steady ramps of force. (a) A force vs. time trace obtained when testing a pairwise EC15 vs. EC15 attachment in the jump/slow ramp mode. The attachment survived the jump at 2,200 pN/sec loading rate to ≈20 pN, then lived for ≈1.5 sec under the subsequent slow ramp of 30 pN/sec, rupturing at ≈55 pN. (b) Histogram of EC15 vs. EC15 rupture forces obtained by using the jump/slow ramp mode demonstrated in a. Rising off scale, the two magenta bins illustrate the small percentage (≈33%) of attachments that broke during the jump, indicating a subpopulation of weak fast-failing EC15 vs. EC15 interactions. The majority (≈66%) of EC15 vs. EC15 attachments survived the jump and split into two narrowly distributed groups, one stronger and longer-lived than the other. Identified by blue and red color-coded curves, the distributions modeling the failure of the two strongly bound substates were matched to the bimodal histogram in b (from the jump/slow ramp test) and to the peak regions in histograms from all steady ramp tests. For the curves plotted here, the off rate for each substate was defined by an exponential dependence on force, krupt ≈ (0.01 per sec) exp(f/5 pN) for the blue substate and krupt ≈ (10–6 per sec) exp(f/3 pN) for the red substate. (c) Illustration of the fit by using Gaussian approximations for the blue and red substate distributions to the data from the steady ramp test at 10,000 pN/sec in Fig. 2b. The dotted-black curve shows the sum of the two distributions, each including the force error. (See Supporting Text and Figs. 8 and 10 for additional details and fits to histograms at other loading rates.) (d) Plot of the most frequent forces in distributions vs. the logarithms of the force rates. The open symbols map the positions of the blue and red substate distributions that matched the force statistics local to the peaks in steady ramp histograms (c). The filled symbols are positions of the two peaks in the histogram from the jump/slow ramp test (b). The errors in these most frequent forces are smaller than the size of the symbols.