Tractography in the clinics: Implementing a pipeline to characterize early brain development

Abstract

In imaging studies of neonates, particularly in the clinical setting, diffusion tensor imaging-based tractography is typically unreliable due to the use of fast acquisition protocols that yield low resolution and signal-to-noise ratio (SNR). These image acquisition protocols are implemented with the aim of reducing motion artifacts that may be produced by the movement of the neonate's head during the scanning session. Furthermore, axons are not yet fully myelinated in these subjects. As a result, the water molecules' movements are not as constrained as in older brains, making it even harder to define structure using diffusion profiles. Here, we introduce a post-processing method that overcomes the difficulties described above, allowing the determination of reliable tracts in newborns. We tested our method using neonatal data and successfully extracted some of the limbic, association and commissural fibers, all of which are typically difficult to obtain by direct tractography. Geometrical and diffusion based features of the tracts are then utilized to compare premature babies to term babies. Our results quantify the maturation of white matter fiber tracts in neonates.

Highlights

• •The proposed method enables consistent tractography in clinical datasets.
• •The tractography is used to structural positioning purposes
• •Geometrical features and diffusion variables in the tracts' paths are analyzed.
• •The gestational age was predicted with regressions in term and preterm babies.
• •The extracted features can be used as indexes of early neurodevelopment.

1. Introduction

Diffusion tensor imaging (DTI) has become one of the most widely used tools for in-vivo brain imaging. However, DTI scanning of neonates is challenging due to both physiological and technical issues. Physiologically, the image quality is affected by the low myelin content, the similarity in water content between white matter (WM) and gray matter (GM) and the differences in axonal packing in the developing brain (Huppi and Dubois, 2006, Huang et al., 2006, Cascio et al., 2007). Technical difficulties stem from the challenge of keeping a non-sedated neonate immobile in the scanner for the required amount of time to obtain good signal-to-noise (SNR) and spatial resolution and a relatively high angular resolution (Huppi and Dubois, 2006). As a result, clinical DTI scanning procedures in neonates use rapid sequences with the hope of avoiding significant motion artifacts, but at the expense of image quality.

DTI methods estimate water displacement. In WM, the primary direction of water motion is radial along the length of the axons. Thus, this technique can also elucidate the pathways and connections between neurons. In practice, DTI tractography gives an approximation of the directions of axonal bundles and provides some insight into brain connectivity. In regards to brain maturity, the connectivity between brain zones may be a more precise marker of development than the contrast between brain structures (Elysia et al., 2009, Walhovd et al., 2010). In particular, it is known that some limbic tracts such as the fornix are established after 19–20 gestational weeks (Huang et al., 2006), and should be visible via DTI methods in neonatal datasets. Some association fibers such as the Inferior Frontal Occipital Fasciculus (IFOF) and the Inferior Longitudinal Fasciculus (IFL) are not entirely developed in term babies (Huang et al., 2006, Liu et al., 2010). Commissural fibers such as the posterior thalamic radiation (PTR) and the anterior thalamic radiation (ATR) form mostly between the last trimester of pregnancy, and these tracts are not fully myelinated until the last gestational week (Prayer et al., 2006). All the above-mentioned neuronal structures are markers of the brain maturity process starting in the womb when the brain begins to form and lasting through the first years of life (Dubois et al., 2006). Hence, a proper assessment of these tracts in individual neonates may serve as a biomarker of brain development.

Unfortunately, while great strides have been made in the research setting using for example multishell diffusion techniques (Kunz et al., 2014), due to the fast imaging sequences employed, most clinical neonatal data sets do not have the required image quality to perform anatomically meaningful tractography.

The explanation as to why low-quality diffusion images are not suitable for tractography has to do with the difficulties in connecting the principal components of the diffusion ellipsoid between voxels. The intervoxel connectivity may be accomplished with one of three algorithms; streamline tracking (STT) (Basser et al., 2000), tensor deflection (TEND) (Lazar et al., 2003) and tensorlines (TL) (Weinstein et al., 1999).

These algorithms use different propagation strategies that lead to more or less smooth tracts. All of them assume a dominant eigenvector tangent to the tract pathway. However, TL, which we'll use here, can be dynamically tuned by a factor ranging between 0 and 1. Hence, using FA in TL, the level of anisotropy also modulates the tensor propagation smoothness.

Despite the slight differences in propagation criteria, the three algorithms use the same stopping critterion, which depends on the level of anisotropy and the local curvature of the reconstructed fiber exceeding a critical value (Conturo et al., 1999). To connect the current voxel with any of the neighboring ones, the inner product is used with a threshold that varies between 0.8 and 0.9, allowing discrepancies in the range 25.8 to 36.8 degrees between concomitant principal eigenvectors (Xue et al., 1999, Basser et al., 2000).

Noise is a major drawback for anatomically accurate tractography, no matter which algorithm is used. Noise can not only deflect the main component of diffusion, in which case, all cited algorithms generate fake tracts and the error is propagated with each created line, but it can also modify the diffusion pattern, and Rician noise (the one encountered in the low SNR regime) has been found to increase the FA erroneously. This combination of effects is the reason for the prolific and anatomically inconsistent tract creation when running tractography in raw clinical data.

However, here our contribution does not depend on the particular tractography used. We perform inter acquisition alignments to enable the creation of a diffusion template. The post alignment averaging of diffusion patterns allows us to diminish the non-correlated information while keeping the correlated our method retains. As the averaging procedure is performed in the tensor domain, one the diffusion patterns overlapped with the ones found in the sample selected as the model.

The alignment together with the selection of correlated regions of the averaging function enhance the SNR and keep the orientation of the primary eigenvectors aligned among acquisitions, the two crucial factors used in the tractography generation.

Here we create a post-processing pipeline that executes DTI tractography in neonatal clinical data. To do so, we create a sharp average template on which tractography can be performed, and the tracts are projected back into the images of individual subjects. We tested the efficacy of our procedure by extracting some of the tracts mentioned above, including the fornix, the IFOF, the ILF, the PTR and the ATR. To this end, we used retrospective clinical data of newborns for which direct tractography could not extract these marker tracts.

Once tracts are generated, we use them to find biomarkers of abnormal development due to prematurity. On average, one in ten neonates in the world is born with a neurodevelopmental condition, and the neurological consequences of preterm birth are the most common plight of babies that survive and are expected to reach the adulthood (Blencowe et al., 2012). These neonates - 15 million yearly worldwide - may suffer from diverse issues such as cerebral palsy, sensory deficits, learning disabilities and respiratory illnesses among others (Cooke, 2005). Some of these disorders are severe enough to prohibit independent functioning, and these conditions are often present during the whole life of the subject (Nosarti et al., 2002, Gardner et al., 2004), generating emotional and financial costs to patients' relatives and society. According to Muraskas and Parsi (2008), in the United States, a stay in the neonatal intensive care units costs 3500 USD per day, and long-term stays can sometimes cost up to 1 million USD. Additionally, the long-term costs and consequences of this condition are difficult to calculate across the lifespan, due to the high diversity of long-term outcomes across subjects. Nonetheless, Peristats (Plains, 2006) estimated at 26.2 billion USD the burden of prematurity alone in the United States in 2007. Both medical and educational expenditure, and lost productivity associated with the condition were included in the calculation.

At the time of writing of this manuscript, and despite enormous advances in scanning protocols and post-processing imaging techniques have been done, it is still difficult to detect some of the subtle abnormalities in human neonatal brains that can affect neurodevelopment, particularly in clinical settings. Finding early biomarkers of abnormal development in premature and term-born children is of primary necessity, and has been put forward as a high priority goal by the World Health Organization (WHO) (Howson and Dkinner, J.l., 2012, Blencowe et al., 2012), as well as important private organizations such as the Gates Foundation (Gates, 2014).

Using machine learning, we have successfully demonstrated that geometrical factors are highly discriminative in a complex problem such as differentiating patients with Alzheimer, mild cognitive impairment and controls (Yepes-Calderon et al., 2014) and hence; we consider that geometrical measurements may be able to characterize development in the same manner. Once an anatomically meaningful tractography is generated, we compute a set of analytical features from the geometries and diffusion variables of the tracts. It is known that myelination correlates closely with neurodevelopment (Popko, 2010, Deoni et al., 2011), and we envisage that a multivariate regression using these geometrical and diffusion-derived features can generate biomarkers of early human development and therefore, set a baseline to elucidate deviations from normality. We test this concept in a dataset of brain MRI images of premature and term-born neonates.

2. Materials and methods

2.1. Neonates data

The datasets contain diffusion MRI scans of 24 term (T) neonates 39.66 ± 0.98 and 25 pre-term (P) neonates 31.66 ± 4.05, both mean values referring to post-conceptional ages (PCA) in weeks. These subjects have been scanned at comparable chronological ages T: 43.58 ± 3.82 and P: 43.59 ± 5.41 PCA. Table 1 gives an overview of subject's scanning times. The images were pulled retroactively from the database at Children's Hospital of Los Angeles (CHLA) and screened for the absence of any delaying pathology. All studies were acquired with a 1.5T GE scanner using 25 gradient directions, a neonatal head coil, b-value = 700 s/mm² and an echo planar imaging (EPI) sequence. Slice thickness varies from 3 to 5 mm. Due to the diverse spatial resolutions found in the clinical database our procedure includes a re-sampling step to enforce comparable voxel sizes. The local IRB at the CHLA approved the use of this retrospective data.

Table 1.

List of clinical subjects in the development test. GA stands for gestational age, PCA for post-conceptional age, PNA for post-natal age and DOS for days of scan. All ages are in weeks.

Item	Term					Preterm
	Serial	Genre	GA	PNA@DOS	PCA@DOS	Serial	Genre	GA	PNA@DOS	PCA@DOS
1	001	F	31	9.43	40.43	030	M	40	2.29	42.29
2	003	M	36	1.29	37.29	031	F	40	4.43	44.43
3	004	F	26	7.00	33.00	032	M	40	1.71	41.71
4	005	F	36	4.86	40.86	033	F	40	1.43	41.43
5	006	M	36	11.29	47.29	034	M	40	2.14	42.14
6	007	M	33	14.14	47.14	035	F	40	8.57	48.57
7	008	M	25	23.29	48.29	036	M	40	10.14	50.14
8	009	F	23	27.00	50.00	037	M	37	5.00	42.00
9	010	F	29	8.29	37.29	039	F	40	8.57	48.57
10	011	M	25	26.00	51.00	040	F	37	2.29	39.29
11	013	M	35	6.14	41.14	043	F	40	1.29	41.29
12	014	F	36	9.14	49.14	044	M	41	3.86	44.86
13	015	M	28	26.14	54.14	046	M	40	1.86	41.86
14	017	M	34	5.71	39.71	047	M	40	1.43	41.43
15	018	F	24	21.86	45.86	048	F	40	1.43	41.43
16	019	M	36	2.43	38.43	049	F	40	4.29	44.29
17	020	M	28	16.14	44.14	050	M	40	0.29	40.29
18	021	M	25	17.14	42.14	052	M	39	0.57	39.57
19	022	F	36	1.00	37.00	053	M	40	12.14	52.14
20	023	M	35	2.71	37.71	055	F	40	12.29	52.29
21	024	M	28	17.86	45.86	056	M	41	0.57	41.57
22	026	F	30	7.43	47.43	057	M	40	4.00	44.00
23	027	M	31	10.57	50.57	058	M	38	1.00	39.00
24	028	F	36	2.00	38.00	343	F	39	2.43	41.43
25	029	F	34	12.00	46.00

2.2. Preprocessing

Pre-processing consists of two steps: skull-stripping and tensor estimation. This preprocessing is performed with MedInria (Toussaint et al., 2007). Skull-striping is accomplished using an automatic algorithm that first averages all diffusion-weighted images (DWI), thus creating a brain tissue enhanced image, and by then removing non-brain tissues using a uniformity criterion. Tensor estimation is done in the log-euclidean (LE) space, as in Fillard et al. (2007). Using the LE avoids the DWI shifting produce by Rician noise, which commonly affects DTI datasets with low SNR. Consequently, diffusion is not underestimated as in the algebraic strategy. The tensor estimation that we use also includes a regularization term that keeps the edges of the tensor field while smoothing homogeneous regions (Fillard et al., 2007).

2.3. Template generation

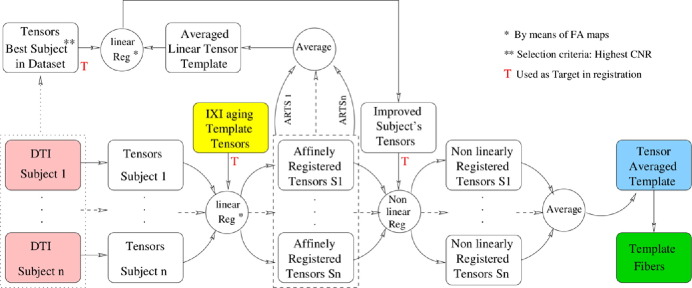
Once the tensors are estimated, we build the template following the process depicted in Fig. 1, which includes both a linear and non-linear registration steps.

Fig. 1.

Schematic description of template generation.

The linear registration removes global differences among all our data sets, including displacement, rotation, scaling and shearing (Jenkinson et al., 2002). For this purpose, we opted to do the tensor registration using the transformation matrix (TM) that results from registering the fractional anisotropy (FA) maps of our datasets to the FA map of a common template (Zhang et al., 2010). Then, the TM is applied to move each sample's tensors to the tensor's space of the template (Jenkinson et al., 2002). This procedure does not affect the integrity of the data since the linear registration only interpolates the structure of the moving samples to the fixed sample.

We then average all the affinely registered tensors to create a linear template. This volume is a combination of blurry images. To retain details in the template, we perform a new linear registration, in which the fixed data is the template, and the moving data is the best acquisition subject among our datasets, where ‘best acquisition’ refers to the highest SNR image. Through this linear registration, a template with improved image quality over individual subjects is created.

For the non-linear registration, we use the algorithm described in Yeo et al. (2009), and implemented in MedInria (Toussaint et al., 2007). In this step, all the affinely registered individuals are non-linearly registered into the new affine template determined above. The non-linearly registered tensors are averaged to create the final template, which we will use in the next sections for extracting tractography in the individual subjects. Finally, we obtain the tensors and tracts in the created template.

2.4. Testing the core enhancing strategy in synthetic data

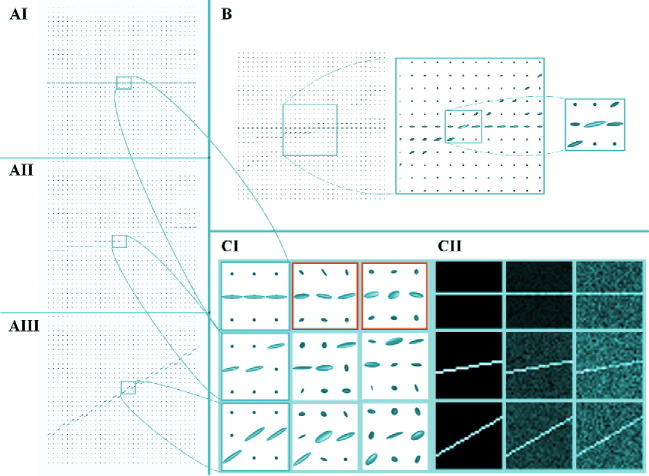
Toy signals were programmatically created using a particles filter that acts on a space restricted by a cylinder of p = 5u and length L = 5 mm as in Barmpoutis and Vemuri (2011). The particles randomly diffuse with preference along the length of the cylinder. Then, we created a 32 × 32 field of view and connected the diffusion models to draw a single fiber. The diffusion patterns follow the rule Fib_i = [cos(α ∗ pi/180), sin(α ∗ pi/180, 0)], which allows pattern rotations in the XY plane. The parameter α in the equation above is zero in the synthetic model signal, and will receive any value in the range [0,90] whenever non-overlapping diffusion signals are simulated among acquisitions. Different levels of Rician noise – $S_i=\sqrt{\left[S_i{+N}_1\left(0,\sigma \right){+N}_2\left(0,\sigma \right)\right]}$ – are induced in the signals to simulate low quality acquisitions. The complete testing set is depicted in Fig. 2.

Fig. 2.

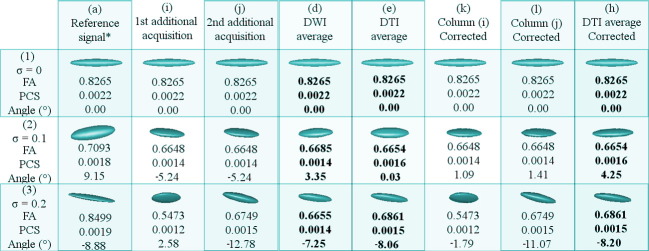
Proof of concept synthetic data. Panel A shows ideal-synthetic-tensor fields: AI is the reference (equivalent to the MoD along this document); AII and AIII are tensor fields simulating acquisition rotated 10 and 30 degrees respectively, about the reference (AI) all in a 32 × 32 pixels field of view. Panel B shows the tensor field that is generated when the three acquisitions (AI, AII, and AIII) are averaged in the DWI-domain. Panel C shows the same information in the tensor and FA domains. Some tensors of Panel A are zoomed-in and shown in the first column of CI. In Panel C, the columns simulate acquisitions with different levels of noise. In CI, the parameters of the tensors are as follows: rows 1, 2, and 3 represent tensors with 0, 10, and 30-degree rotations, respectively. Columns 1, 2, and 3 represent tensors with 0, 0.1, and 0.2 sigma noise, respectively, except the tensors in the red boxes, in which the noise levels are generated with σ = 0.5 and σ = 0.15 (left and right, respectively). Each cell of CI is a zoomed version of the field from which the FA of the images on CII are generated; positional correspondence is kept.

With this information, we focus on demonstrating that our method is capable of correcting the intentionally induced rotations and the misalignment caused by noise. To this end, we center the analysis in a center diffusion pattern where all the signals converge in the rotated framework. If the signals at this point are aligned, the rest of the diffusion voxels should follow. We compared the outcomes of our method with different image quality enhancement strategies used in the field, including the DWI averaging applied during acquisition through the avg. parameter. See the results in Section 3.1.

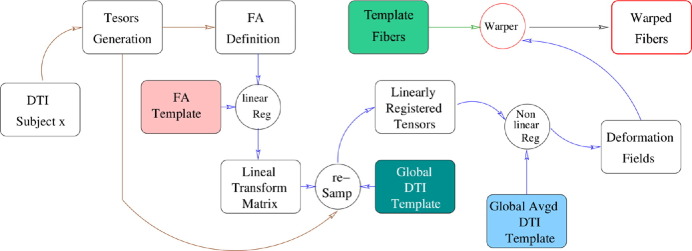
2.5. Subject warping

To extract the tensors' field and the tractography in each subject of our dataset, we non-linearly register the tensor images of the linearly aligned subjects to the final template using the algorithm described in Yeo et al. (2009). From this, we obtain a set of displacement vectors, the deformation fields (DFs) at each voxel. Finally, the DFs are applied to the tracts in the template, creating the tracts in the subject. This warping step is created using MedInria (Toussaint et al., 2007). Our method is illustrated in Fig. 3.

Fig. 3.

Warping strategy for subject tractography.

2.6. Neonatal brain development marker tracts

We test our template-based method by obtaining the brain development-marking tracts mentioned in Section 1. For this purpose, we choose two regions of interest (ROI) and apply an AND operator in the fiber tracking algorithm. This procedure is done using MedInria (Toussaint et al., 2007). ROI positioning in the template is determined by an expert pediatric neuroradiologist. For the fornix, one ROI is located in the body of the fornix and the other in the columns zone. For the IFOF, a coded-colored FA map is used. The first ROI was located in the green colored path that connects the temporal and parietal lobes in an image that appears few slices anterior of the splenium of the corpus callosum in a coronal view. The second ROI was located in a slice anterior to the fornix, in a circular green spot that traverses the corticospinal tract (Wakana et al., 2007).

For the ILF, we proceed similarly to the IFOF. In the FA coded-colored map we identify the coronal slice that crosses the posterior edge of the cingulum. Then, we select as first ROI all colored zones included in the hemisphere of interest. A second ROI is placed in the most posterior coronal slice in which the frontal lobe is disconnected from the temporal lobe. Then all fibers in the temporal lobe are selected (Wakana et al., 2007).

For the ATR, the first ROI is placed in the entire thalamus on the coronal image and the second one in the anterior limb of the internal capsule (Wakana et al., 2007). For the PTR, the first ROI is drawn in the entire thalamus on a coronal image and the second one in the occipital lobe (Wakana et al., 2007).

FA levels of 0.1 and 0.05 are chosen as a trigger and stopping conditions for all tracts.

2.7. Characterizing normality and prematurity

The following features are extracted in all subjects and for each studied tract: volume (vol), fibers' lengths (fibl), fractional anisotropy (FA), apparent diffusion coefficient (ADC), lambda1 (L1), lambda 2 (L2), lambda 3 (L3), relative anisotropy (RA), volume ratio (VR). For all listed variables except the volume, we used the mean value for computations.

This data is inputted into the Python Data Analysis Library (PANDAS) (McKinney, 2011) data frame and posteriorly analyzed by systematic linear regressions, where the dependent variable was set as the gestational age at birth (GA). These features were used as predictors of GA.

3. Results

3.1. Aligning synthetic data

The eigenvalues and eigenvectors that describe the diffusion geometry are dependent on the accuracy of the overlays of concomitant diffusion patterns. The results of these experiments are shown in Fig. 4, Fig. 5. Recall that the analysis on the center voxel imposes the hardest challenge due to the overlapping of the three signals. The rotational correction capability exposed here should be translated to any other voxel in the field of view. Also, consider that after linear registration, the diffusion patterns end up being overlapped, but the diffusion patterns retain the orientation that they had before the linear transformation. Hence the necessity of re-orientating the diffusion patterns voxel by voxel.

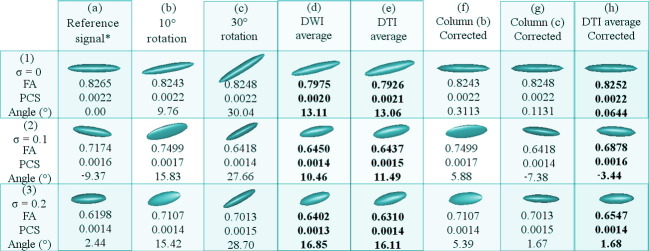
Fig. 4.

Results of the theoretical experiment using the new pipeline on synthetic data with rotation induction. Column (a) contains the tensor of the reference DWI signal. Columns (b) and (c) hold tensors of the DWI signals that have been rotated 10 and 30 respectively, respect to the x-axis. Column (d) represents the tensor of the DWI signal that has been averaged using (a), (b) and (c) in the DWI domain without any prior rotation correction. Column (e) shows the same information as in (d), but all done in the tensor field. Column (f) and (g) contain the corrected tensors of Columns (b) and (c), respectively. Column (h) displays the result of averaging the tensors in Columns (a), (f) and (g).

Fig. 5.

Results of the theoretical experiment using the proposed pipeline on synthetic data with no rotation induction. Column (a) contains the tensor of the reference DWI signal. Column (i) and (j) hold tensors of the two additional DWI signals that have been randomly generated. Column (d) represents the tensor of the DWI signal that has been averaged using (a), (i) and (j) in the DWI domain without any prior rotation correction. Column (e) is the same as (d) but all done in the tensor domain. Column (k) and (l) hold the corrected tensors of Columns (i) and (j), respectively. Column (h) displays the tensor that has been averaged from the tensors in Columns (a), (k) and (l).

For both Fig. 4, Fig. 5: row (1) displays the dataset with ideal conditions (no noise), row (2) the one with σ = 0.1, and row (3) that with σ = 0.2. Value of Angle (°) is the nearest angle (in degrees) of the principle eigenvector with respect to the x-axis. Abbreviations: FA (fractional anisotropy); PCS (principal component of the diffusion ellipsoid geometry); σ (variance of Rician noise). Also note that in the sets marked with * (reference signals), the value of σ is 0.5 units lower than in the additional acquisitions for the experiments affected with noise. The columns with bold entries correspond to definitive results and should be used for the comparisons.

In the experiments with synthetic data, the proposed method always aligns the additional acquisitions to the model dataset, thus improving the overlap between structures and consequently cleaning the images while retaining the essential information in the dataset. This remains true even in the datasets affected by noise. Note also how all the factors that affect the tractography are favorably adjusted.

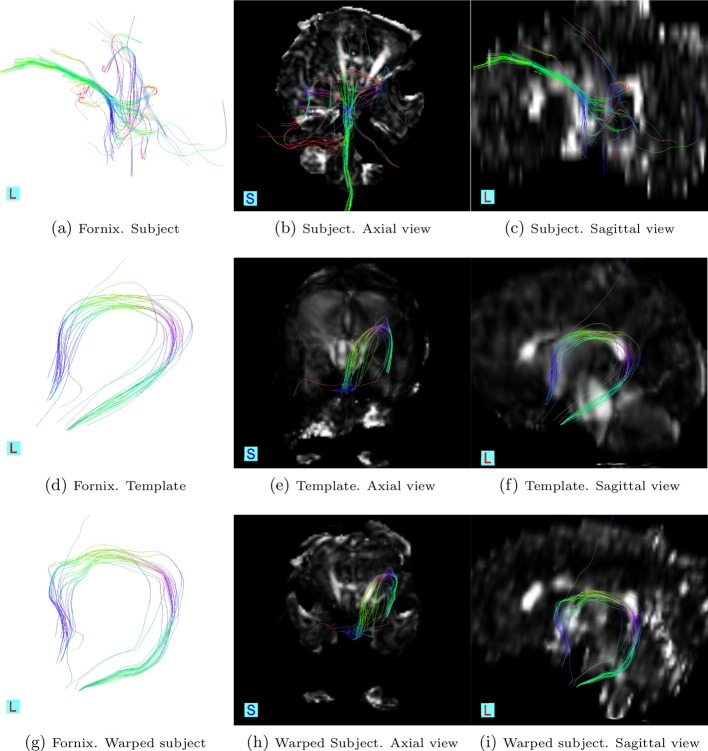
3.2. Limbic structure: the fornix

The fornix is located near the splenium of the corpus callosum and diverges from the mid-sagittal zone at the level of the crus just before the fibers reach the hippocampus (Kendi et al., 2008). The correct location of the fornix in our findings, just below the corpus callosum, is seen in the sagittal views of both the template and the warped subjects. The extracted fornix presents red colored fibers at the level of the crus, which is consistent with the lateral displacement anatomically described in the literature (Fig. 6).

Fig. 6.

Fornix tract. Rows (from top to bottom): In a subject before to post-processing, in the template and the warped subject. Columns (from left to right): stand-alone tracts, tracts in axial view and tracts in sagittal view.

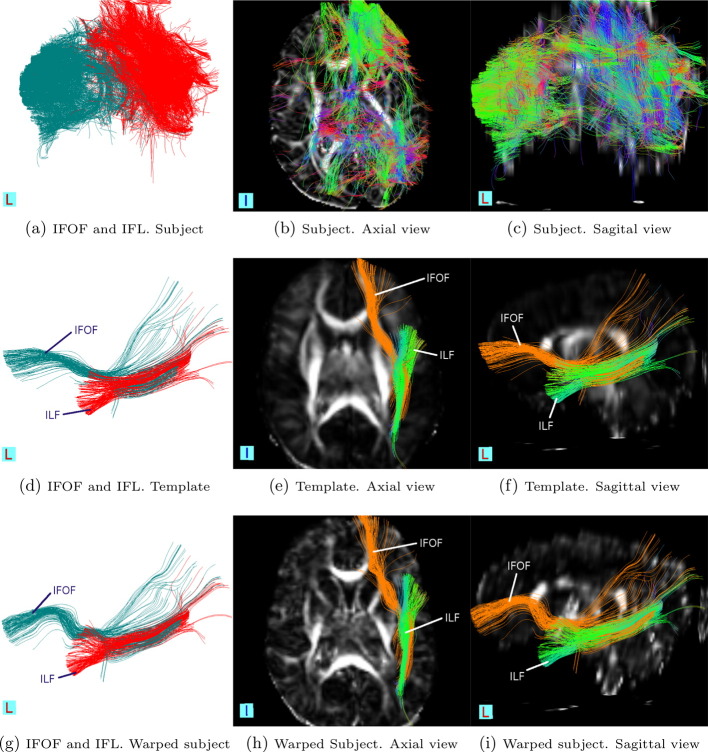
3.3. Association structures: the IFOF and the ILF

The ILF connects the occipital cortex with the anterior temporal lobe and amygdala, whereas the IFOF begins in the occipital cortex, continues medially through the temporal cortex dorsal to the uncinate fasciculus, terminating in the orbitofrontal cortex (Philippi et al., 2009). The tracts found in Figs. 7d–i are consistent with this description.

Fig. 7.

Association tracts (IFOF and ILF). Rows (from top to bottom): in a subject before to post-processing, in the template, and in the warped subject. Columns (from left to right): stand-alone tracts, tracts in axial view and tracts in the sagittal view.

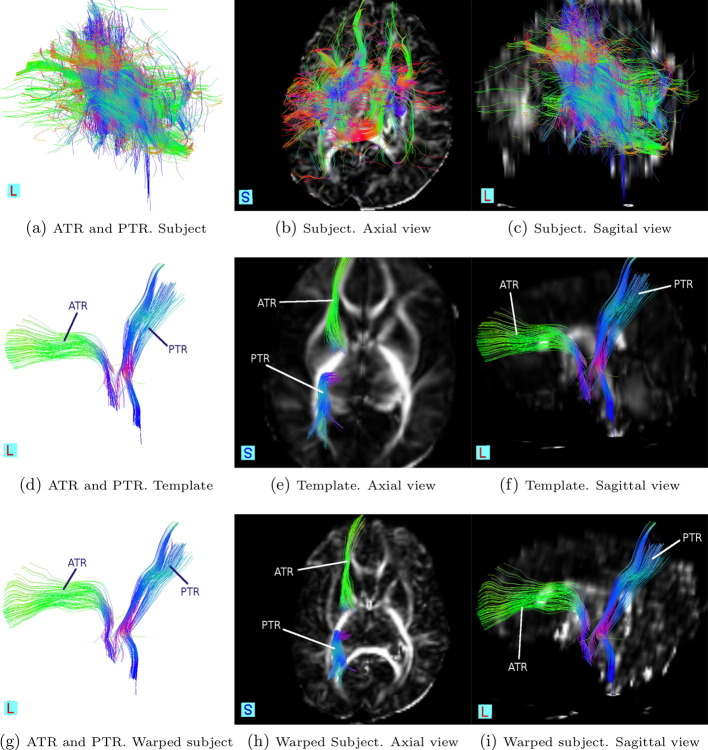
3.4. Commissural structures: the ATR and the PTR

The ATR consists of fibers between mediodorsal thalamic nuclei and the frontal cortex, and fibers between anterior thalamic nuclei and the anterior cingulate cortices (Mamah et al., 2010). This tract is most anatomically accurate in the warped subject as seen from Fig. 8i, where the contrast of the overlapped FA map permits the localization of the tract in the brain.

Fig. 8.

Commissural tracts. Rows (from top to bottom): in a subject before to post-processing, in the template, and in the warped subject. Columns (from left to right): stand-alone tracts, tracts in axial view and tracts in sagittal view.

3.5. Characterizing neurodevelopment

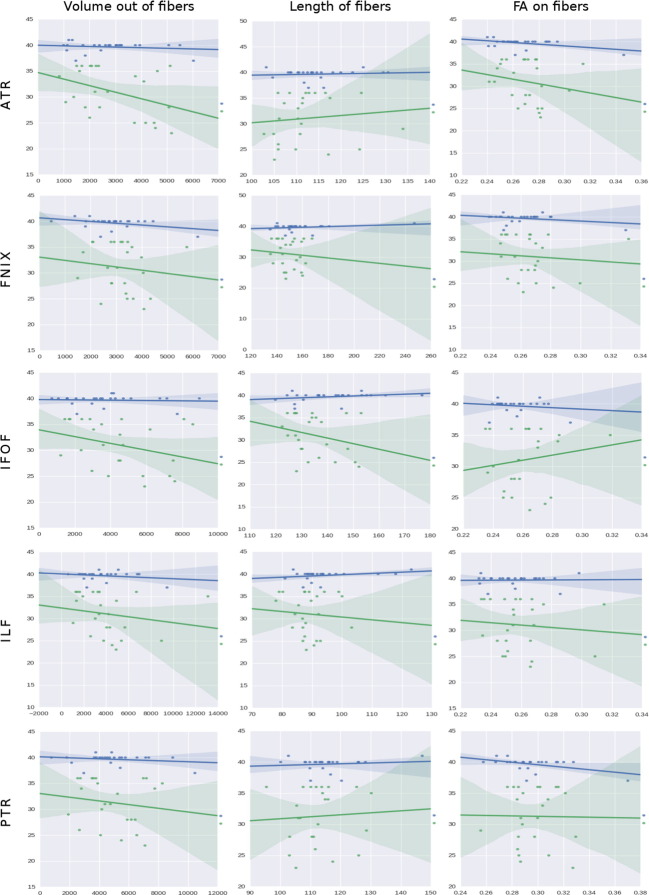
Fig. 9 shows the regression of GA using volume, length and FA as predictors. The leftmost column corresponds to the volume created by the fibers for both the terms and preterms, and show a reduction as the neonates grow older. This in agreement with what we know of the underlying biology of white matter tracts, where maturation is accompanied by packaging and better definition of tract boundaries. It is remarkable that all the white matter structures that we analyzed show the same pattern of development for this feature. Additionally, these plots indicate that packing (as characterized by volume) is happening faster in the preterm group, perhaps as they are trying to ‘catch up’ to the term subjects.

Fig. 9.

Regressions on GA using, from left to right columns: volume, length and FA as predictors (X-axes). The rows represent all the tracts found in 3.1, 3.2, 3.3. The Y-axis of each plot correspond to the dependent variable which we aim to predict, in this case the GA, and data comes from the column GA in Table 1. The Y-axis range, given in weeks, is automatically configured in the plots by the dispersion present in the independent factors studied. The X axis is the independent factor which is defined in the header of each figure. The units of the X axis have been omitted to favor the visualization; thus, the trending patterns are emphasized. It is our intention to see if those trends can be associated with developmental insights. Note that the length of fibers is giving in mm while the volume is presented in mm³. The rest of variables belong to the diffusion derived group, and their units are the standard ones for dMRI in humans. Finally, the condition is always the birth time, classified as a boolean value for the term (blue) and preterm (green) subjects.

The length of the white matter fibers (the middle column of Fig. 9) increases with age in the normal group for all five white matter structures. At neonatal ages, proliferation, pruning, and myelination take place simultaneously in a process that shapes the brain connectivity by prioritizing the neurons with strong connections (Rakic and Zecevic, 2000). However, in the preterm group, increasing length with age is only seen in the commissural tracts (ATR, PTR). According to Prayer et al. (2006), the PTR and ATR reach full myelination at week 41 in term babies. Since the scans were taken around week 43 GA, we may be capturing the recovering process of the preterm babies.

Interestingly, both early developing (fornix - 19–20 week of gestation) and late developing tracts (ILF, IFOF, not developed at birth) in the pre-term group are shortening instead (Huang et al., 2006, Liu et al., 2010). The negative slope for prematurity in the fornix and the association structures should not be interpreted literally as a shortening of tracts. Instead, for example for the late developing association tracts, the preterm brain might be in the proliferation state that happens before pruning and retraction. If more connections are taking place, the water diffusivity should be more isotropic, which stops the tractography algorithm earlier. Both proliferation and retraction are present during maturation, and alternatively leading to the formation or destruction of structures.

Regarding the FA results in the right column of Fig. 9, there is slight decrease in FA in term born babies for all structures. In the preterm case, the FA also decreases for all structures, except for the IFOF, where the FA increases. Again one might consider the competing processes of proliferation, pruning, and myelination, where for example proliferation may reduce FA, while myelination increases it.

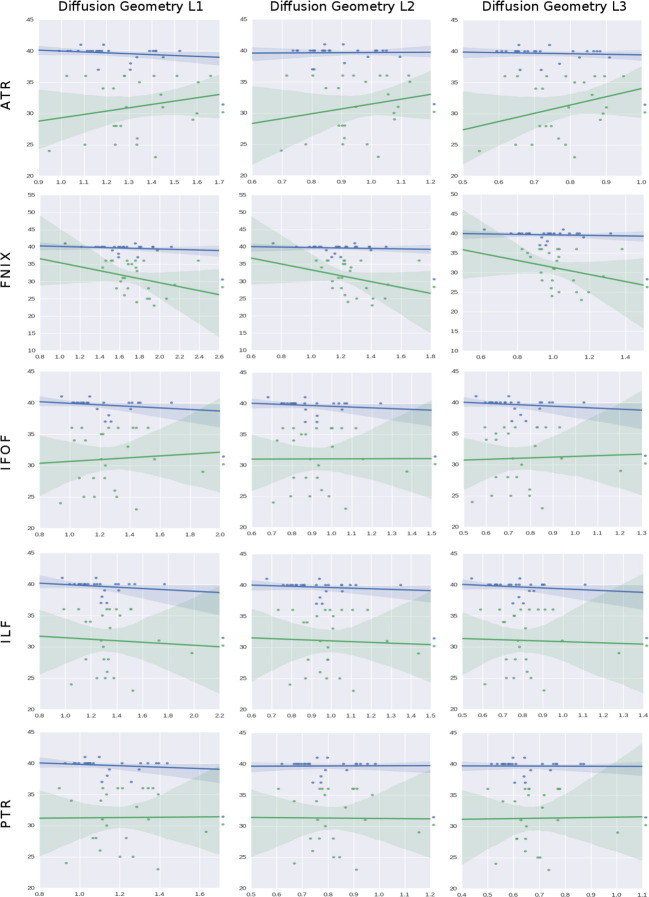
The plots of L1, L2 and L3 in Fig. 10, correspond to the (ordered) eigenvalues or diffusivities, and help to explain the findings in the FA mentioned above. As seen in the first column, the negative slope in the FA readings of term babies is the consequence of a reduction in the principal axis of the ellipsoid. When this component is reduced, and the other two eigenvalues are kept constant or grow, the diffusion turns progressively into isotropic, resulting in reductions in FA. This finding suggests that the transverse diffusion is increasing with age, growing while the diffusion parallel to axons diminishes. Given the results of Fig. 9 that the volume is reduced with age, and that the length of the fibers is growing simultaneously, one can infer that the change in transverse diffusion is a measure of changes in metabolic activity; basically, these neurons have increased the interchange of fluid with its surroundings and therefore, the transversal diffusivity - with respect to L1 - grows.

Fig. 10.

Regressions on GA using, from left to right columns: the 3 (ordered) diffusion tensor eigenvalues, L1, L2 and L3, as predictors (X-axes). The rows represent all the tracts found in 3.1, 3.2, 3.3. The Y-axis of each plot corresponds to the dependent variable which we aim to predict, in this case the GA, and data comes from the column GA in Table 1. The Y-axis range, given in weeks, is automatically configured in the plots by the dispersion present in the independent factors studied. The X axis is the independent factor which is defined in the header of each figure. The units of the X axis have been omitted to favor the visualization; thus, the trending patterns are emphasized. It is our intention to see if those trends can be associated with developmental insights. Note that the length of fibers is giving mm in while the volume is presented in mm³. The rest of variables belong to the diffusion derived group, and their units are the standard ones for dMRI in humans. Finally, the condition is always the birth time, classified as a boolean value for the term (blue) and preterm (green) subjects.

In the case of the preterms subjects, the slopes increase or decrease consistently with the FA values obtained. Note, however, that the diffusion ellipsoid in the fornix shrinks faster than in any other structure; the overall effect is a slight increase in the isotropy of the diffusion pattern. This means that the water is being hindered equally in all directions, potentially due to proliferation and retraction events, hence the reduction in the overall diffusion. The IFOF is the only structure whose FA increases in preterms. The combination of L1, L2, and L3 reveals that this is due to an increased diffusivity in the principal axis of the ellipsoid, but in general, its diffusion pattern does not differ much from the one in the ILF.

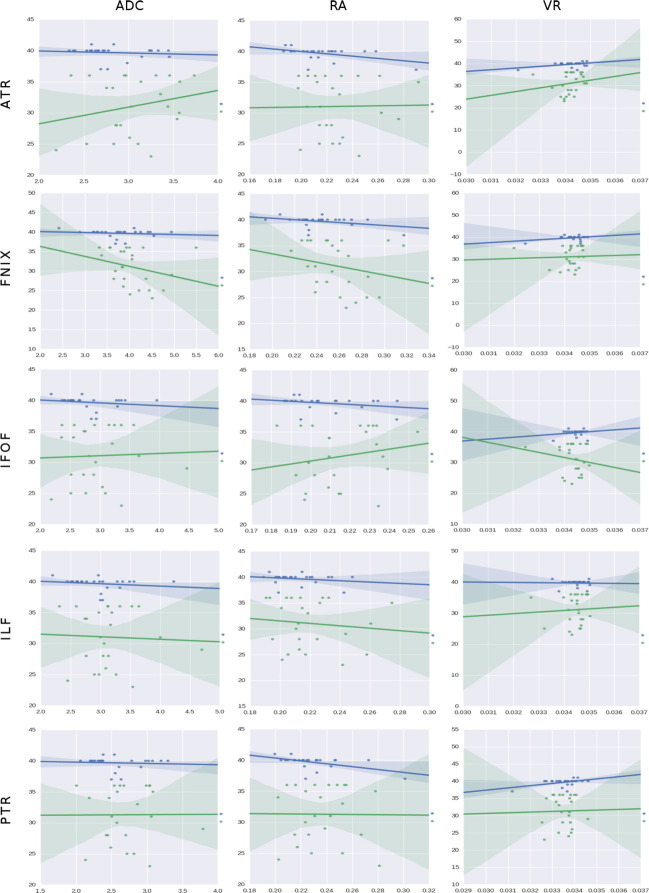
Fig. 11 shows the regression values for the ADC, RA, and the VR. The ADC is the addition of the three diffusivities. In all the term-born structures, the ADC tends to decrease slightly with increasing GA. Possibly water displacement is being hindered, but as can be seen in the L1, L2, and L3 regressions plots, this hindering is happening in all directions. In the preterm group, the commissural tracts - ATR and PTR - are growing. Recall that these structures are supposed to be formed at birth, but here in the preterm group growth is delayed, and recovering. The fornix and association structures show a descending ADC that might be associated with the prevalence of proliferation activities.

Fig. 11.

Regressions on GA using, from left to right columns: apparent diffusion coefficient (ADC), relative anisotropy (RA) and volume ratio (VR) as predictors (X-axes). The rows represent all the tracts found in 3.1, 3.2, 3.3. The Y-axis of each plot corresponds to the dependent variable which we aim to predict, in this case the GA, and data comes from the column GA in Table 1. The Y-axis range, given in weeks, is automatically configured in the plots by the dispersion present in the independent factors studied. The X axis is the independent factor which is defined in the header of each figure. The units of the X axis have been omitted to favor the visualization; thus, the trending patterns are emphasized. It is our intention to see if those trends can be associated with developmental insights. Note that the length of fibers is giving in mm while the volume is presented in mm³. The rest of variables belong to the diffusion derived group, and their units are the standard ones for dMRI in humans. Finally, the condition is always the birth time, classified as a boolean value for the term (blue) and preterm (green) subjects.

The RA, in the center column of Fig. 11, can be used for clinical assessments similar to those from the FA, in fact, results here are almost exactly like the ones shown in the left column of Fig. 9 for FA.

The VR is the ratio between the volume of a bounding ellipsoid and the one of the sphere created with a radius equal to the mean diffusivity. As the average diffusivity is reduced over time in most of our samples and the sphere resides in the denominator of the expression, VR tends to go up with age. The only exception is again in the IFOF.

4. Discussion

In this manuscript, we presented a method that recovers meaningful information from tractography in datasets that originally did not have the required quality to do so, as is often the case in the clinic. The efficacy of the pipeline was proven by obtaining tracts usually difficult to see when direct tractography is used. The gist of the method lies in the fact that the created local template is of much higher quality than any of its individual contributors (Goodlett et al., 2009). The averaging used to create the model ideally improves the SNR $\sqrt{\left(n\right)}$ times, with n being the number of averaged subjects (Gonzalez and Woods, 2002). The posterior FA-based warping of fibers in the template enables fiber representation in original datasets.

The registration processes depicted in Fig. 1, Fig. 3 are performed on the tensor fields, and include a tensor rotation before averaging. With the tensor rotation, we ensure the correct structural overlapping of subjects before the averaging process.

According to Prayer et al. (2006), cerebral myelination is a predominantly postnatal process, progressing in a craniocaudal direction and centrifugal manner. A manifestation of this process is seen when comparing the PTR in the template and the subject (Fig. 8e and h). The shorter fiber projections of the PTR to the occipital lobe in the subject are an example of incomplete or delayed development. The unmyelinated fibers yield almost isotropic FA readings in those regions on the subject, and as a result, the tracts appear shorter.

To quantify the differences in diffusion variables along tracts, we analyzed each feature according to its capacity to retrieve the gestational age at birth. While non-linear models may more accurately represent long-term development, we used linear models given the short age span of this study. We used the model to compare preterm and term neonates.

The main goal of the method here is to design a tractography algorithm and diffusion-based measures that are useable in the clinic, given low quality image data. Few other works have looked at tractography in neonates. For example, Kinz et al. (2014) the authors recruited 13 neonates and performed muti-shell acquisitions with uniform spatial resolution and diffusion parameters. Subjects were scanned during sleep with a multishell scheme that included 6/50, 9/250, 12/700, 16/1400 (gradients directions/b-values in s/mm²) and the whole protocol was completed in 9 min and 30 s including a high-resolution T2 scan. These scans used 32 channels to speed up acquisitions. While this work did a great job of elucidating tractography in neonates, these protocols are not feasible with current clinical setups. For example, in hospitals, typically 8 channels are used for parallelization, with advanced setups going up to 16 channels. Furthermore, the voxel size in Kinz et al. (2014) is 4 to 5 times bigger those used in our clinical setup. Bigger voxels improve the spin recruitment and thus the SNR, at the expense of losing the capacity to track changes smaller than one voxel. More importantly, while the focus of research projects such as Kinz et al. (2014) is to identify group wise characteristics, the clinic requires a patient-oriented analysis, which our method provides. Similarly, Brown et al. (2014) looked for associations between neurodevelopment and connectivity. Subjects were scanned using a research protocol including uniform voxel size and diffusion parameters. The authors included DWI averaging to improve the quality of the images, but, to reduce scan time, sacrificed angular resolution by scanning with only 12 directions. In the clinics, DWI averaging is rarely used, but higher angular resolutions are often preferred.

5. Conclusions

A method to process information from archived low-quality DTI datasets has been proposed and tested. It uses no other images than the datasets to be treated. We improved the tractography performance to the point that we could obtain limbic, commissural and association tracts in the brain, something that we could not accomplish with standard tractography on 1.5T clinical data.

Our procedure is suitable to process clinical DTI data, which is abundant in hospitals but often not usable for research due to its lack of uniformity. Hospitals keep this data for legal reasons, but it is usually stored with no prospect for further use. Recovering this information is of outstanding importance since it represents one of the most extensive databases covering controls, pathologies, and special cases. Our method may allow the use of new and stored DTI medical images for rich background referencing, diagnosis and treatment determination and research.

The association between tract development and underlying biological facts was also studied, using diffusion variables extracted with the pipelines depicted in Fig. 1, Fig. 3. While our sample of 49 subjects in two groups is relatively small, our results show a remarkable coherence with what is known of early developmental biology, and corroborate our initial hypothesis: diffusion parameters and tractography in particular are useful predictors to characterize early human brain development. However, in the future, more subjects will be added, and a multivariate analysis will be used, to obtain clinically useable indices of development.