Figure 10.

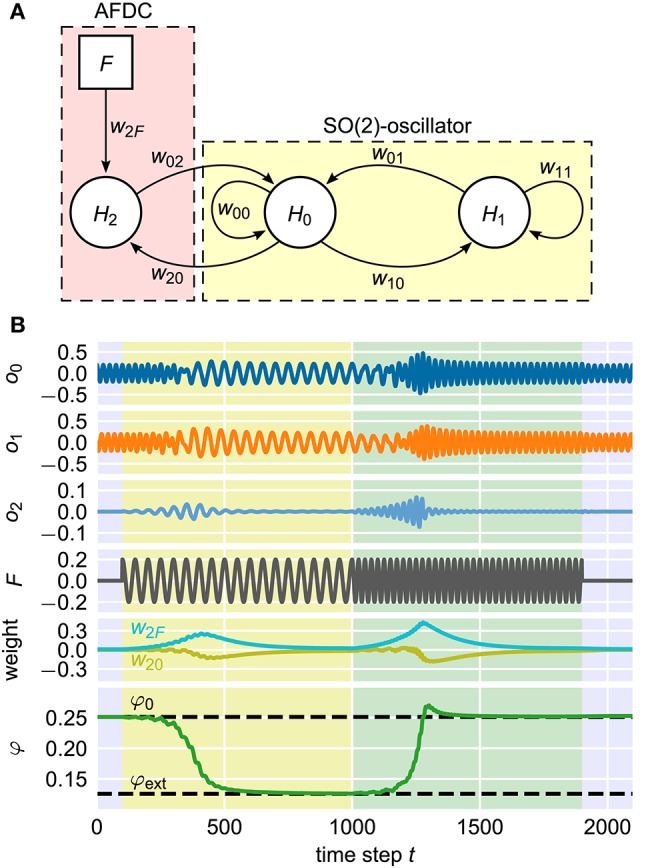
Neural implementation of the AFDC mechanism. (A) The neurons H₀ and H₁ are fully connected by the synapses w₀₀, w₀₁, w₁₀, and w₁₁ and form a neural SO(2)-oscillator. The neuron H₂ calculates the signal P which is the weighted difference between the external signal F and the activity value of H₀. Accordingly, the weight w_2F corresponds to the coupling strength ϵ and the weight w₂₀ represents the variable β of the AFDC mechanism. The weight w₀₂ can either be fixed at a positive value or adapted with similar dynamics as w₂₀ and w_2F. (B) Example adaptation of the neural oscillator. It is initialized with an intrinsic frequency of f₀ = 0.04 corresponding to a value of φ₀ = 0.25 of the internal frequency determining variable. At time step t = 100, an external signal with a frequency of f_ext = 0.02 is applied until time step t = 1, 000 (yellow shaded area). For 1, 000 < t < 1, 900, the frequency of the external signal is changed to f_ext = 0.04 (green shaded area). For t ≥ 1, 900, there is no external signal. Shown from top to bottom are the activities o_i of the neurons H_i (i ∈ {1, 2, 3}), the external signal F, the synaptic weights w₂₀ and w_2F and the frequency determining variable φ of the SO(2)-oscillator.