Figure 11.

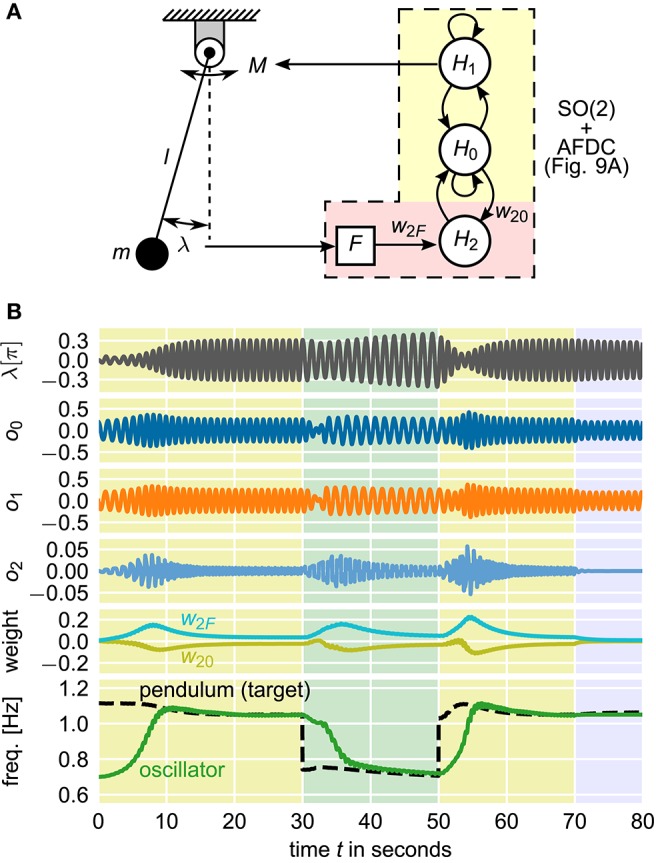
Closed-loop pendulum control using a neural SO(2)-oscillator with AFDC mechanism. Energy-efficient control is realized if the pendulum is driven at its resonant frequency. (A) The output o₁ of neuron H₁ controls the torque M driving the pendulum with length l and mass m. The current angular displacement λ is converted into the external signal F which is fed back to the adaptive oscillator. The neural network is updated with a frequency of 25Hz. (B) Simulation of the system with varying pendulum length l. The initial length of the pendulum is l₀ = 0.2m. At t = 30 s, the length is changed to l₁ = 0.4m. At t = 50 s, the original length l₀ is restored. At t = 70 s, the feedback connection from the pendulum to the oscillator is cut to demonstrate that the oscillator has indeed learned the correct frequency to drive the pendulum. Shown are the current angular displacement λ of the pendulum, the outputs o₀, o₁, and o₂ of the three neurons, the synaptic weights w_2F and w₂₀ of the plastic synapses of the AFDC mechanism, and the intrinsic frequency of the oscillator and the resonant frequency of the undamped and undriven pendulum (target frequency for the oscillator). The resonant frequency of the pendulum does not only depend on the current physical properties of the pendulum but also on the current amplitude of its oscillations.