Motion Correction for Diffusion Weighted SMS Imaging

Introduction

Diffusion-weighted imaging (DWI) is commonly used in clinical MRI, in particular in the assessment of stroke, demyelination, or cortical lesions [1], [2]. It also plays an important role in scientific studies of structural connectivity [3]–[5].

Although DWI sequences usually use fast readouts, such as echo-planar imaging (EPI), DWI scans commonly last several minutes, especially when used for diffusion tensor imaging (DTI). These long scans result in sensitivity to head motion [6], [7]. Motion correction with external optical tracking can improve DWI data quality [8]–[11]. However, affixation of tracking markers can be challenging and marker “slippage” during the scan will compromise the quality of motion correction or even introduce artifacts [12], [13].

Parallel imaging makes it possible to shorten the EPI readout for diffusion imaging [14], [15], and thereby reduce echo time (TE) or increase spatial resolution. However, this does not substantially reduce acquisition times, due to the rather long weighting gradients required for DWI combined with typically extensive slice packages, which results in prolonged repetition times, TR. In contrast, simultaneous multislice imaging (SMS) makes it possible to acquire several slices simultaneously [16]–[19] and can considerably shorten volume acquisition times for DTI protocols. However, this gain in scanning efficiency is often used to acquire more complex DWI protocols (such as multiple b-values, more diffusion directions, and higher resolution), reintroducing the problem of patient motion.

Motion correction for SMS-DWI can therefore be expected to improve DWI acquisitions. However, the effect of motion, including prospective motion correction (PMC), on SMS acquisitions and reconstructions, has not been investigated. Therefore, we incorporated prospective motion correction into diffusion weighted SMS imaging and investigated the influence of motion, motion correction, and relative coil motion on the reconstructed data. The algorithm described in [20] was extended to incorporate SMS reconstruction into multiplexed sensitivity encoding (MUSE) [21], [22]. Additionally, a technique was implemented to address potential marker slippage during prospective motion correction with external optical tracking, using intrinsic position information of the volumetric data.

Methods

All experiments were conducted on a 3T Tim Trio system (Siemens Healthcare, Erlangen, Germany), using a 32 channel head-coil. External tracking was performed with an in-bore camera system (Metria Innovation Inc. Milwaukee, USA) [23]. Tracking markers were attached using double sided tape. A single spin-echo EPI sequence with diffusion weighting was modified to allow for continuous real-time position updates [9], SMS acquisition [18], [24], and acquisition in either single-shot or segmented mode. A variable number of non-diffusion weighted scans (b=0 images) were distributed evenly over the acquisition. The orientations were defined by the electrostatic repulsion algorithm [25]. Unless otherwise stated, online SMS reconstructions of single-shot data were performed using the sliceGRAPPA implementation as distributed with blipped-CAIPI EPI (https://www.nmr.mgh.harvard.edu/software/c2p/sms). In vivo acquisitions were performed in accordance with the local regulations and all subjects provided verbal and written consent using a protocol approved by our Institutional Review Board.

Multiplexed Sensitivity Encoding (MUSE) for segmented acquisitions

Segmentation of the EPI readout allows for higher resolution and better SNR. However, segmented EPI scans are notoriously sensitive to motion due to phase corruption, requiring adjustment of phase between in the acquired segments of k-space. We used a dedicated reconstruction algorithm (MUSE, [10], [21]), based on a two-step SENSE [14] reconstruction. In a first step, each under-sampled segment is reconstructed separately. Phase information from this reconstruction is combined with the coil sensitivity maps, and utilized in a second SENSE reconstruction step that integrates all segments of k-space into a full data set. This technique can be used for single-slice and SMS reconstructions alike [21], [22].

This study comprised a set of experiments.

1. PACE-XPACE: integration of image-based and external motion feedback

The external tracking system provides position information in 6 degrees of freedom (3 rotations and 3 translations) which are represented in the affine transformation matrix A_Extern [26]. Independently, the vendor-provided Prospective Acquisition CorrEction (PACE) algorithm yields the transformation matrix A_PACE through real-time volumetric registration to the first scan [27]. However, since the diffusion weighed data required additional offline reconstruction (MUSE), the PACE mechanism was modified to provide feedback only based on the non-diffusion weighted scans. Clearly, unlike the external tracking data, the PACE updates will be available only sparsely, depending on the number of b=0 images interspersed into the time series.

If prospective motion correction with external tracking perfectly tracks head motion, then all intrinsic PACE updates would return the identity matrix. Therefore, when external tracking is enabled, the matrix A_PACE represents an error term, for instance, if the tracking marker shows slippage relative to the brain. Consequently, the position information from the two sources can be combined into a single transformation A_final, by multiplying the data from the tracking system (A_Extern) with the inverse of the PACE feedback (A⁻¹_PACE):

$${\mathrm{A}}_{\text{final}}={\mathrm{A}}_{\text{Extern}}*{{\mathrm{A}}^{-1}}_{\mathrm{P}\mathrm{A}\mathrm{C}\mathrm{E}}.$$ [1]

Intrinsic motion feedback from the imaging data will therefore allow correction matrix (A_final) to be “reinitialized” during the course of the scan (after acquisition of each b=0 volume).

A phantom experiment was performed to evaluate this approach. A structured phantom was equipped with two tracking markers and placed inside the head-coil. Both targets were visible to the camera.

In a reference experiment, tracking information from a single target was transferred the XPACE motion correction algorithm. During the DWI measurement, the phantom was intentionally moved between b=0 scans and this motion was prospectively corrected using tracking information A_XPACE from the first marker.

In a second experiment, external tracking was then manipulated by switching tracking data from the first to the second marker (within a scan), creating intentional errors in motion correction and hence position errors. These errors are detected by the PACE algorithm and the positional information A_PACE is introduced to the final transformation matrix according to Eq. 1.

If a certain selectable threshold (overall rotation or translation) of residual motion A_PACE is exceeded, according to the image-based volumetric registration, then a subset of the measurement is repeated. A subset is defined a set of diffusion weighted images between adjacent b=0 scans. A motion threshold of 1.5 mm or 1.0 degrees was empirically found to be safely beyond the noise level and provides a good compromise between potential data loss and scan time prolongation. Also, the potential number of repetitions was limited to ensure acceptable scan duration. In the current implementation, this was achieved by specifying a maximal number of rejections. After this number is reached, no further rejection is accepted. However, the measurement will still be motion corrected. Sequence parameters: TR/TE: 4400/65ms, TA: 5min, resolution: 1.5×1.5×2mm³, 2 segments, matrix: 128×128, partial Fourier = 5/8, 45 slices, SMS factor 1, diffusion weightings b₁= 500 s/mm² with 30 directions and 6 b=0 scans. The phantom was manually rotated after the first b=0 volume. While this rotation leads to flow artifacts in our water-filled phantom, the long TR left enough time for any water motion to settle before the next b=0 volume.

2. Effect of virtual motion on the coil sensitivities

Separation of simultaneously acquired slices requires knowledge of the coil sensitivity profiles, either in the form of coil-sensitivities (SENSE) or a reconstruction Kernel (GRAPPA). Motion changes the relative position between the object and the receiver coils, and therefore may introduce errors into reconstructed images. To investigate the influence of such misalignments on the slice-GRAPPA reconstruction, a phantom experiment was performed using artificial motion feedbacks as described in [28]. This techniques uses position input form a text file to update the acquisition during runtime. This allows for very well defined position changes. Note, that this virtual motion only changes the position of the FoV, and therefore the position relative to the acquired coil sensitivities, while the signal distribution within the object remains unchanged. Several artificial pose changes (2 degrees, 2 mm, and 10 degrees in plane) were generated between b=0 volumes after the slice-GRAPPA kernel was computed at the initial object position.

During the course of the measurement, the position offset is registered by the volumetric PACE motion algorithm and fed back to the scanner as A_PACE, to test the PACE functionality during SMS acquisitions. The volumetric data was used to correct for the artificial position change and re-establish conformity with the slice-GRAPPA kernel.

Sequence parameters: TR/TE: 1500/60ms, TA: 0.5min, resolution: 2×2×3mm³, 1 segment, SMS factor 3, matrix: 96×96, 45 slices, diffusion weightings b₁=500 s/mm² with 12 directions and 5 b = 0 scans.

3. Augmented MUSE: post-hoc adjustment of coil sensitivities in case of real motion

Augmented SENSE [20] describes a theoretical framework which allows initial coil sensitivity data to be adapted to motion-induced changes in object poses with regards to RF coils. It assumes precise knowledge of the coils sensitivities, even somewhat beyond the boundaries of the measured object.

We extended the augmented SENSE framework to MUSE reconstructions (hence “augmented MUSE”), by adapting the coil sensitivities for the two MUSE reconstruction steps described above.

In the first step, the image of one segment is reconstructed using augmented SENSE:

$$s_1(t)=\int C^{\prime }(\mathit{r}){\rho }_1(r)e^{-i{k}_1(t)\mathit{r}}d\mathit{r}$$ [2]

Where s1(t) is the acquired signal from one segment and k₁(t) is the generalized 3D SMS k-space as described in [29]. C’(r) is the receiver coil sensitivity C(r) which is modified with the transformation matrix from the external tracking data:

$$C^{\prime }(\mathit{r})=C(\mathit{r})*A_{\mathit{\text{extern}}}$$ [3]

As described in [30], the general MUSE formulation can be written as a system of equations for L acquired segments:

$$s_1(t)=\int [C^{\prime }(\mathit{r})e^{i{\phi }_1(\mathit{r})}]\rho (\mathit{r})e^{-i{k}_1(t)\mathit{r}}d\mathit{r}\cdots s_L(t)=\int [C^{\prime }(\mathit{r})e^{i{\phi }_L(r)}]\rho (\mathit{r})e^{-i{k}_L(t)\mathit{r}}d\mathit{r}$$ [4]

Where φ_1‥L are the image phases calculated from the undersampled data of each segment (equation 2) which are now multiplied with the modified coilsensitivities C’(r) (equation 3).

The impact of motion versus coil sensitivities was first investigated in a phantom experiment. During a DWI measurement, the phantom was moved multiple times, primarily by rotational movements (up to 20 degrees). This motion was corrected prospectively using XPACE tracking. Offline SENSE reconstruction was then performed first without modifications to the coil sensitivity maps, and then using maps adjusted for the corrected motion.

Sequence parameters: TR/TE: 1700/55ms, resolution: 1.5×1.5×2mm³, SMS factor 3, 2 segments, matrix: 128×128, 45 slices, diffusion weightings b₁=200 s/mm² with 30 directions and 6 b=0 scans.

Next, the augmented MUSE experiment was repeated in vivo. A volunteer was instructed to move as much as the head-coil allows. This resulted in motion patterns with amplitudes of 10 mm and 5 degrees. Three in vivo acquisitions were performed: (a) No motion (for reference), (b) motion without correction and (c) motion combined with prospective correction. Data from the motion-corrected experiment (c) were reconstructed twice, using regular SMS-MUSE with unmodified coil sensitivities, and using augmented MUSE reconstruction.

Sequence parameters for the in vivo scans were: TR/TE: 2000/80ms, resolution: 1.5mm isotropic, SMS factor 3, 2 segments, matrix: 128×128, 45 slices, diffusion weightings b₁=1000 s/mm² with 30 directions and 6 b=0 scans.

Results

The effectiveness of the PACE-XPACE combination is shown in Figure 1. Panels a-d display one slice of the b=0 images collected at four time points during the phantom experiment. Panel (a) shows the phantom in the original position. In (b) the phantom was moved manually, but the movement was prospectively corrected using the external tracking system. The movement of the small air bubble at the top of the phantom reflects the changing orientation. The third time-point (1c and c*) shows images acquired after switching tracking to the second marker, which introduces a position offset (c) that is then detected and retrospectively corrected by re-alignment with PACE (c*). Panel (d) shows the re-acquisition of volume c after the prospective correction data was adapted to the intentionally modified marker position (as per Eq. [1]).

Figure 1.

A single slice of a DWI experiment at 4 time-points (no diffusion weighting). Phantom (a) in the original position, (b) after manual movement, updating the imaging volume using external tracking. The air-bubble on the top indicates the change in orientation. (c) A shift in marker position introduces an error term to the correction matrix. (c*) The PACE algorithm detects and corrects for this error term. (d) The measured marker displacement is taken into account during subsequent position updates, and the image shows good agreement with the original position shown in panel a).

Figure 2 shows the effects of motion on the validity of the coil sensitivity maps in a phantom. Tracking data from a text file were used to introduce a defined artificial movement. The first column (a) shows the phantom in its original position at the beginning of each measurement. In the second column (b) three in-plane movements were generated: 10 degrees rotation (first row), 2 degrees rotation (second row), and 2 mm translation (third row). These results show that only large movements (10 degrees) appear to have a substantial influence on the reconstruction (b, top row, pointed out by the arrow). In panel c, these artificial movements were then detected and corrected by the volumetric registration in PACE followed by the acquisition of a new data set. No residual artifacts are seen when the artificial motion was corrected (c), in accordance with expectations for virtual motion.

Figure 2.

Artificial motion was introduced to a phantom acquisition using position data from a text file. One slice of a phantom a) in the original position b) with artificial file motion c) after PACE motion correction is shown. Different movements were simulated (10 degrees, 2 degrees, 2 mm). A window with higher contrast (b) highlights the artifacts due to misalignment with the coil sensitivities.

Figure 3 shows an average of all images acquired during the prospective motion correction experiment without (a) and with (b) additional adaption of the coil sensitivities using augmented MUSE. For each case, three simultaneously acquired slices are displayed. Comparing the two images (Fig. 3, a and b), it can be seen that adjusting coil sensitivities improves reconstruction (as pointed out by the arrow). However, some remaining artifacts can still be seen using augmented MUSE (b).

Figure 3.

Real motion was prospectively corrected using external tracking. Three simultaneously acquired slices are shown a) with no modification of the coil sensitivities b) with augmented MUSE. In the upper left corner, the contrast was enhanced to show remaining artifacts.

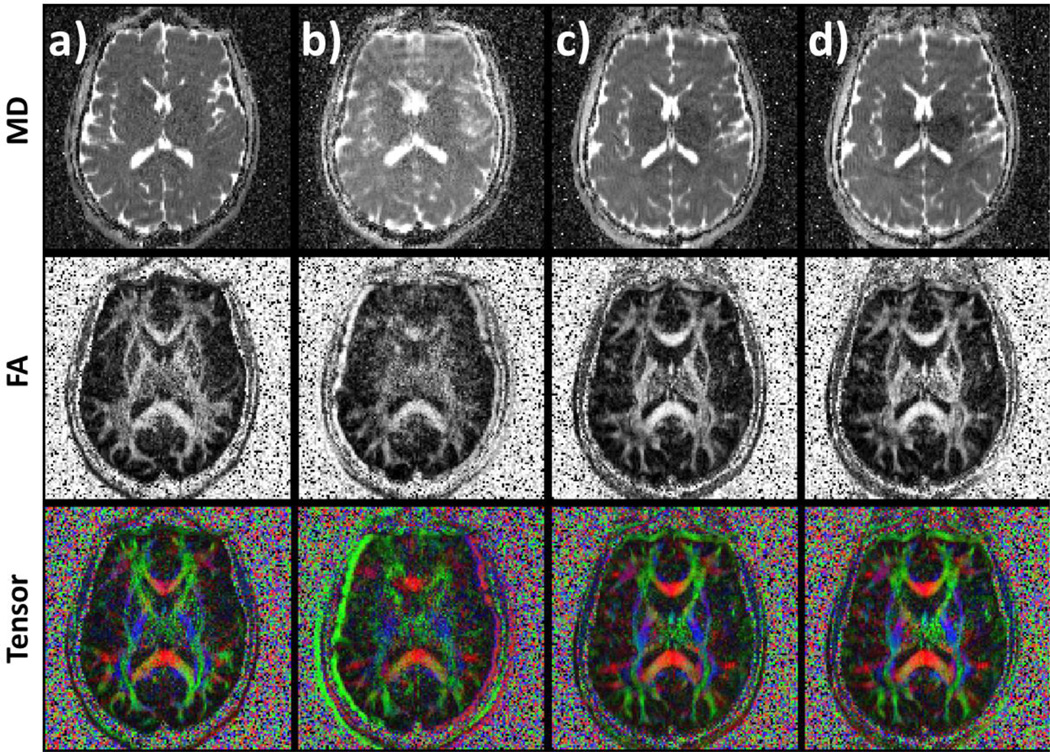
The results of the in vivo experiments are summarized in Figure 4. Images were acquired without motion (a), with motion but no PMC (b), with motion and prospective correction (c), and motion with PMC + augmented MUSE (d). The motion was up to approximately 10 mm translation and 5 degrees rotation, and similar across acquisitions. Motion markedly reduces the image quality compared to the no-motion case (b versus a). Prospective motion correction substantially improves results (c versus b). In the in vivo study, the use of augmented MUSE did not visibly improve the data (d versus c), despite the relatively large motion. When motion corrected data (c and d) is compared to the ‘no motion’ case (a) a slight blurring can be observed after motion correction due to residual misalignment of the imaging data.

Figure 4.

Shown are the mean diffusivity (MD, first row), fractional anisotropy (FA, second row) and tensor maps (third row). Images show data acquired a) without motion for comparison b) with motion, without correction c) with prospectively corrected motion. Additionally, the third dataset was reconstructed using augmented MUSE (d).

Discussion

This work investigated the influence of motion and its correction on SMS imaging. We investigated the use of prospective motion correction with external tracking, the use of volumetric navigators using intrinsic positional information, and a combination of both approaches. Additionally, the influence of inconsistencies between coil and imaging data on the SMS reconstruction was investigated. We have shown, following the theoretical framework shown in [20], that coil sensitivities can be adapted to motion while having only minor influence on the presented vivo DTI data.

The use of prospective motion correction with external tracking is advantageous and allows for extremely fast position updates [8]–[10], [23], [26], [30]. However, instabilities due to incorrect motion correction have also been reported [12], [13]. The combination of external tracking data with image-based navigator information can help overcome this problem. While external tracking can provide information at high rates (30–100Hz), the navigator data delivers occasional updates that allow a recalibration of the correction matrix of the external tracking system. While this work uses PACE as intrinsic tracking method [27], which is particularly appropriate for fMRI and DTI acquisitions, other navigator approaches [31]–[34] could be incorporated and make the method available to other imaging or spectroscopy techniques. The current implementation was restricted to segmented and SMS acquisitions. However, it should be feasible to extend the technique to more complex acquisition schemes. Since parallel imaging relies on the correct information to reconstruct non-acquired data points (SENSE: sensitivity maps; GRAPPA: kernel), the effect of motion and its correction need to be evaluated. Therefore, we investigated the effect of motion on single-shot SMS as well as on segmented EPI acquisitions, which involve additional in-plane under-sampling in the first reconstruction step. Our experiments show that small movements (up to about 2 mm and 2 degrees) have only minor effects on parallel imaging reconstructions and can be neglected in practice. It is to be noted, that the virtual motion experiment only reproduces some relevant motion effects and the artifact behavior in case of the true motion may be enhanced by the additional phenomena, such as coil loading or susceptibility-induced field changes.

For larger movements (>10 degrees), ghosting-like residual aliasing can be seen even after motion correction. We demonstrated an improvement in image quality with Augmented MUSE in a phantom experiment. Crucially, Augmented MUSE relies on the knowledge of coil sensitivities outside the object, obtained by extrapolation of the sensitivities. In practice, large movements may violate this requirement. While it might be possible to demonstrate these effects on selected in vivo raw images, no visible influence was observed on the processed DTI data, even in the case of extreme movements. To the contrary, our results indicate that the effect of motion-induced changes in coil sensitivities may be negligible, especially for motions that are typically encountered, or accepted, in practice. These observations might be specific to the coil setup used in this study, and motion in a receiver array with smaller elements (where the same motion would yield larger relative changes in sensitivities) may have more substantial effects. In addition, the purely qualitative investigation of a single subject was not sufficient to investigate potential changes in DTI data. However, recent studies report similar findings and state notable effects in BOLD fMRI with parallel imaging for rather large head motions in the range of 5mm and 5degrees [36], [37]. In the future, Augmented MUSE for DTI will be included in studies with larger cohorts to investigate quantitative effects on the DTI data.

In summary, we investigated the benefits of image-based and external motion correction on simultaneous-multislice diffusion-weighted acquisitions at 3T. Integrating optical and image based motion correction effectively removed errors related to slippage of the optical marker, which is one of the challenges for external motion tracking [12], [13]. Furthermore, motion-induced inconsistencies in coil sensitivity profiles resulted in small but noticeable errors in SMS reconstruction of phantom data. We introduced augmented MUSE to improve segmented EPI reconstructions, but observed only negligible qualitative differences in the in vivo dataset investigated in this work.

Highlights.

• Prospective motion correction for simultaneous-multislice diffusion-weighted acquisitions is proposed.

• Image-based and external tracking methods are investigated separately and in combination. The synergy of these techniques offers improved stability for marker based prospective motion correction.

• Results also indicate that the effect of motion-induced changes in coil sensitivities may be negligible for motions that are typically encountered.