A Comparison of Methods For Estimating the Incidence of HIV Infection in Repeat Blood Donors

Abstract

BACKGROUND

HIV incidence in repeat blood donors has been estimated by 7 methods. While incidence is always calculated as cases/person-time, approaches to selecting cases and calculating person-time vary. Incidence estimates have not been compared among methods.

STUDY DESIGN AND METHODS

The methods were compared in a simulation study. Because three methods use information from donations made before an estimation interval, 8 years of donation and infection history were simulated, with years 7 and 8 treated as the estimation interval for all methods. An exponential random variate was assigned to each donor to simulate time to infection. Infection risk was constant over 8 years in one scenario but increased at various rates in 7 others. The infection risk scenarios were combined with 4 mixes of donation frequency to generate 32 test conditions.

RESULTS

Three methods produced biased estimates under all conditions. Three others were biased under most conditions. Bias from most methods increased as donation frequency declined. The single method that consistently produced unbiased estimates was the only method that involved the standard epidemiological approach of tabulating all interdonation intervals (IDIs) within the estimation interval. Bias was eliminated from one of the consistently biased methods by a simple modification that involved the average IDI in a sample of donors.

CONCLUSION

The standard epidemiological approach is recommended if required data are available. Otherwise, the modified method involving the estimated average IDI should be considered. Investigators should use caution when comparing incidence estimates among studies with different estimation methods and/or donation frequencies.

INTRODUCTION

Because they are tested for HIV and other TTIs at every donation, repeat blood donors provide a convenient source of longitudinal data for estimating incidence of viral infections. There are at least seven methods in the literature for estimating HIV incidence in donors.^1–18 While under all seven approaches incidence (I) is estimated as I = cases/total time at risk, the methods differ in how cases are identified and time at risk is calculated. The potential effects of these differences on incidence estimates have received little attention.

In this report, estimates from these seven published methods are compared by applying them to the same datasets in a simulation study. We chose simulations rather than a comparison based on actual donation data because of an important limitation of the latter. Using donation data, we can determine whether estimates from two methods do or do not agree but we have no basis for determining whether either estimate is close to being correct. With simulations, we can compare methods using data produced under defined conditions. In particular, we can start by comparing estimates from the seven methods when simulated data are derived from the probability model and the study design that gave rise to the equation for incidence above (more on this later). We may refer to this as comparing methods under ideal conditions. We then perturb the conditions under which the data are generated to determine which methods are robust to departures from the assumptions underlying the incidence equation. One key assumption is that infection risk is constant over the interval of interest. We make this assumption in the initial simulations. We then consider the behavior of the methods when infection risk is increasing over time. We do so because of concern among the public and the blood banking community about the effect of changes in blood banking policy that allow potentially higher risk individuals to donate. To address these concerns, we need to be able to accurately monitor the effect of changes in policy on infection incidence and residual risk.

MATERIALS AND METHODS

Methods from the literature

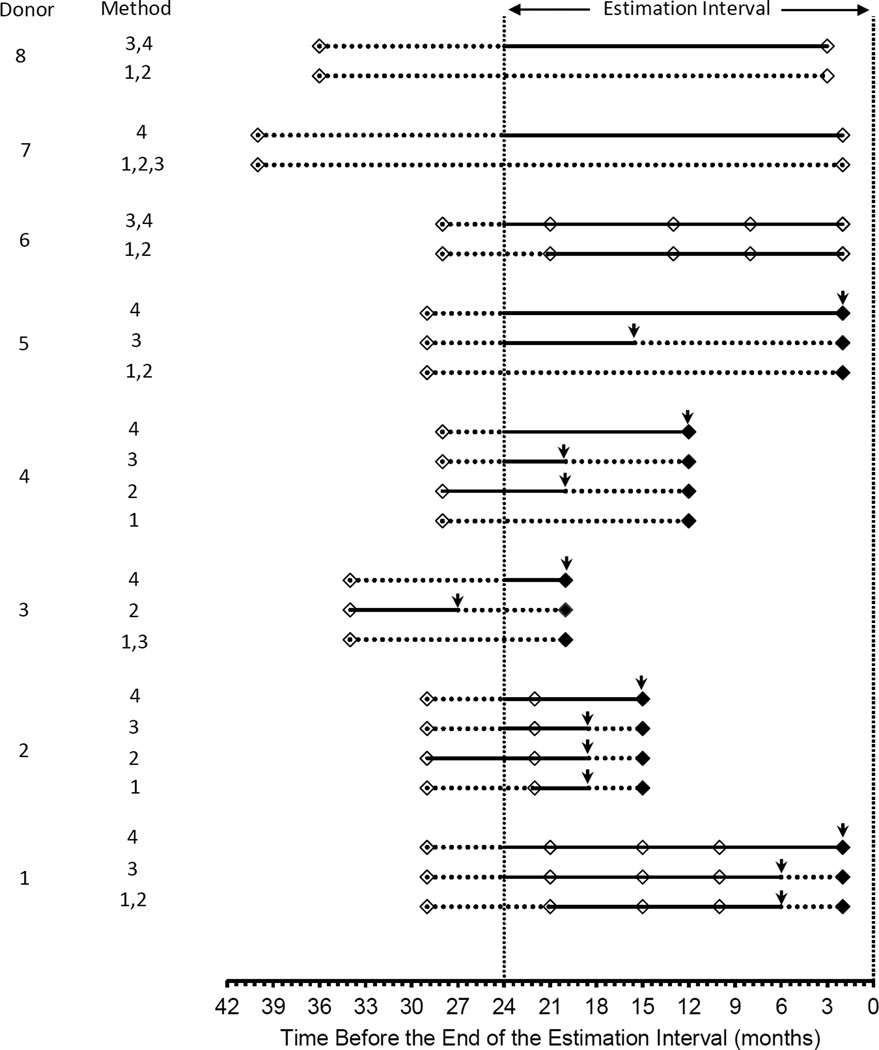
The specifics of the seven methods for estimating infection incidence, as extracted from the published literature and, in some cases supplemented by direct communication with study authors, are summarized below. Methods 1–4 and 7 are illustrated in Figure 1, using donation data from 8 hypothetical donors. The hypothetical donors were constructed solely to illustrate differences in selection of follow-up time and cases among the methods. Methods 5 and 6 do not lend themselves to this form of illustration so they were excluded from the plot.

Figure 1.

Hypothetical donation patterns to illustrate differences among estimation methods in the donors and follow-up time included in incidence estimates. Solid line segments indicate follow-up time that is included in an estimate. Dashed line segments indicate follow-up time that is not included. Open symbols indicate uninfected donations, while solid symbols indicate infected donations. Vertical arrows indicate time of infection assumed in the incidence rate calculations for cases that are included in the estimates. An infected donor is included in the numerator of an incidence estimate only if at least part of the follow-up time for that donor is included in the denominator (e.g. donor 5 methods 1,2 vs donor 5 methods 3,4).

Method 1.^1–5

Select all donors with at least two donations in the estimation interval. For those who remain free of infection through the last donation in the interval, time at risk is time from first to last donation in the interval (Figure 1, donor 6). For those found to be infected at the second or subsequent donation, time at risk is time from the first donation in the interval to half way between the last donation at which the donor was uninfected and the donation at which infection was detected (Figure 1, donors 1 & 2).

Method 2.^6,7

Select donors with at least one donation in the estimation interval. Treat each donor’s last donation in the interval as that donor’s index donation. Exclude any donors with an interdonation interval (IDI) of >2 years prior to the index donation (Figure 1, donors 5, 7, 8). For uninfected donors, time at risk is time from first to last donation in the two year window that ends with the index donation (donor 6). For donors found to be infected at the index donation, time at risk is time from the first donation in the two year window to half way between the last donation without infection and the index donation (Figure 1, donors 1–4).

Method 3.^8–11

Find all IDIs of 3 years or less that end in the estimation interval. If an IDI ends without infection and it starts in the estimation interval, then the entire IDI contributes to time at risk. If the previous donation was given prior to the start of the estimation interval, then only time from the start of the estimation interval to the end of the IDI is included (Figure 1, donor 8). For IDIs that end with infection, define the time of infection to be the midpoint of the IDI. Discard the IDI and the case if the midpoint is before the start of the estimation interval (Figure 1, donor 3). Otherwise, include the case. Time from the start of the IDI to the time of infection is included in time at risk if the IDI starts in the estimation interval (Figure 1, donors 1&2), or time from the start of the estimation interval to the time of infection if it does not (Figure 1, donors 4&5).

Method 4.^12,13

This is very similar to Method 3 but with two key differences. First, the 3-year upper limit on the IDI under Method 3 is not included under Method 4. Longer IDIs are allowed, as long as the IDI ends with a donation in the estimation interval (Figure 1, donor 7). Second, cases that are identified at the end of an IDI that starts before the beginning of the estimation interval are handled differently. Under Method 4, such a donor would contribute a partial case to the numerator of the incidence equation with the contribution equal to the proportion of the IDI that falls in the estimation interval (Figure 1, donors 3–5).

Method 5.^14,15

Select all donors who donated at least once in the 2 year estimation interval and at least once prior to the estimation interval. Using only donors who were uninfected at the last donation in the estimation interval, find the total number of donations in the estimation interval and the number of uninfected donors. Divide total donations by total donors to get donations/donor. Divide by 2 to get donations/donor/year. Invert this to get the IDI. For each donor, multiply the average IDI by the number of uninfected donations in the estimation interval. For each infected donor, add the full time from the last negative to the first positive donation.

Method 6.¹⁶

Select all donors who donated at least twice in the 2 year estimation interval. Apply the algorithm in Method 5 to select cases and calculate time at risk.

Method 7.^17,18

Select all donors who donated both in the estimation interval and at least once prior to the estimation interval. Calculate the average IDI using all IDIs that are fully contained within the estimation interval (Figure 1, donors 1, 2 &6). Do not include any time from an IDI that begins before the estimation interval and ends in the estimation interval. For each donor, multiply the average IDI by the number of donations in the estimation interval.

One problem with the aggregate published literature in which Methods 1–7 have been applied is the lack of a consistent definition of a repeat donor. In some studies, a repeat donor designation referred, either implicitly or explicitly, to individuals who donated prior to an estimation interval.^{3,5,13,14,15,17,18} In other studies, there was no discussion of whether a history of donation prior to the estimation interval was part of the definition.^1,2,4,8,16 In those studies, the only stated requirement was that a donor made at least two donations in the estimation interval. In a third group of studies, donors were included in the incidence estimate (and therefore defined as repeat donors) if they made at least two donations, only one of which was required to have been made in the estimation interval.^6,7,9–12 In the simulations, we used the definitions provided by study authors for each estimation method.

Simulation Studies

The simulations were constructed to estimate incidence during a two year estimation interval. Because methods 2, 3 and 4 make use of information from donations made prior to the estimation interval, 8 years of simulated donation and infection history were generated. Years 7 and 8 were treated as the estimation interval. The equation for incidence estimation arises from the assumption that the risk of infection is constant, which implies that time to infection follows an exponential probability distribution. Therefore, in the initial simulations, time to infection was generated for 100,000 simulated donors by drawing 100,000 random variates from the exponential distribution with parameter 0.0001, which corresponds to an incidence rate of 1 per 10,000 PY (i.e., I=10/10⁵ PY). The zero point for time to infection in the simulations was the beginning of year 1 of the 8-year interval. The assumed incidence rate is the target against which estimates were compared to assess accuracy. In subsequent simulations, the parameter of the exponential distribution increased over time for reasons presented earlier (Table 1). The target for assessing accuracy remained I=10/10⁵ PY under all circumstances tested. In scenarios 2–7, the incidence rate was modeled as rising from year 2 to year 7 and then held constant in years 7 and 8. Scenarios 2 and 3 involve gradual increases in incidence over several years, whereas Scenarios 4–7 involve abrupt increases of various sizes at the end of year 6. In scenario 8, incidence continued increasing in years 7 and 8 but averaged to the same rate (10/10⁵ PY). This latter scenario allowed for determining the effect of violations of the assumption of constant incidence during the estimation interval on our incidence estimation. Under all of the scenarios, simulated donors with infection times >8 years were considered uninfected throughout a simulation. Donors with infection times <8 years were either excluded as prevalent cases or included as incident cases depending on the timing of the infection and the estimation method.

Table 1.

The incidence rates (cases/10⁵ PY) assumed in eight sets of simulations

	Year
Incidence Scenario	1	2	3	4	5	6	7	8
1	10	10	10	10	10	10	10	10
2	5	5	6	7	8	9	10	10
3	5	5	5	5	6.67	8.33	10	10
4	5	5	5	5	5	5	10	10
5	6.25	6.25	6.25	6.25	6.25	6.25	10	10
6	7.5	7.5	7.5	7.5	7.5	7.5	10	10
7	8.75	8.75	8.75	8.75	8.75	8.75	10	10
8	5	5	5.5	6.5	7.5	8.5	9.5	10.5

Each simulated donor’s time at first donation was randomly assigned such that approximately 12.5% of donors began donating in each year. The sequence of IDIs following the initial donation was generated as 56 days, which is the minimum IDI allowed between red cell or whole blood donations in the US, plus a random variate drawn from an exponential distribution, using a separate random variate for each donation. Each donor’s donation series was truncated at 8 years or at the first donation after time to infection; i.e. the first donation after time to infection was treated as the point at which infection was detected.

Donor return behavior is too heterogeneous to be captured by a single probability distribution for time to return. Therefore, donation histories were created for three subsets of donors using three separate exponential parameters for time to next donation. The parameters were selected to simulate three quite different average IDIs (Table 2, left column). Four sets of donation histories were produced by varying the percentage contribution of the three subsets to each set. The average IDI was shortest in Set 1 and longest in Set 4.

Table 2.

Frequency distributions of assumed parameters for time between donations

IDI* (days)		Percent of simulated donors
Mean	Median	Set 1	Set 2	Set 3	Set 4
117	98	85	30	5	5
208	161	10	55	50	10
360	267	5	15	45	85
Weighted average IDI (days)		138	204	272	333
20th, 80th percentile		72, 125**	82, 285**	98, 397**	111, 505**
Median donations, yrs 7 & 8		5	4	3	2

^*includes the 56-day minimum IDI allowed in the US

^**excluding those >2,920 days (8 years)

The simulation process was repeated 4,000 times for each of the 32 combinations of an infection scenario (Table 1) and a mix of donation histories (Table 2). Methods 1–7 were applied to each of the simulated data sets. Mean estimated incidence and the associated 95% confidence limits were then calculated from the 4,000 estimates from each method. A method was considered approximately unbiased under a given incidence scenario if the confidence limits included 10/10⁵PY; i.e. if the method could accurately reproduce the value assumed for years 7 and 8 in the simulations. If the confidence limits excluded 10/10⁵PY, then a method was considered biased.

Modification of published methods

We also considered modifications of three of the seven methods as follows:

In two reported studies, only donors with a history of donation prior to the estimation interval were included in incidence estimation by Method 1^3,5, whereas there was no mention of a requirement for prior donation in the three other studies in which Method 1 was used^1,2,4. Therefore, Method 1 was applied to the simulated data with and without the requirement for a donation before the estimation interval.

In published studies in which Method 3 was employed, the estimation interval varied, ranging from 1.5 to 5 years; thus in some but not all studies the estimation interval exceeded the 3-year window for selecting cases and calculating a donor’s contribution to time at risk. However, in our simulations, the window for selection exceeded the estimation interval. To determine whether using a window for selection that was shorter than the estimation interval would affect the results from Method 3, we repeated the simulations for this method using selection windows of 1 and 2 years.

We also considered a modified form of Method 7 under which the incidence estimate was based on donors who made at least two donations in the estimation interval and follow-up time was calculated by multiplying the average IDI by the number of IDIs for each donor rather than the number of donations. The modified approach is labeled Method 8.

RESULTS

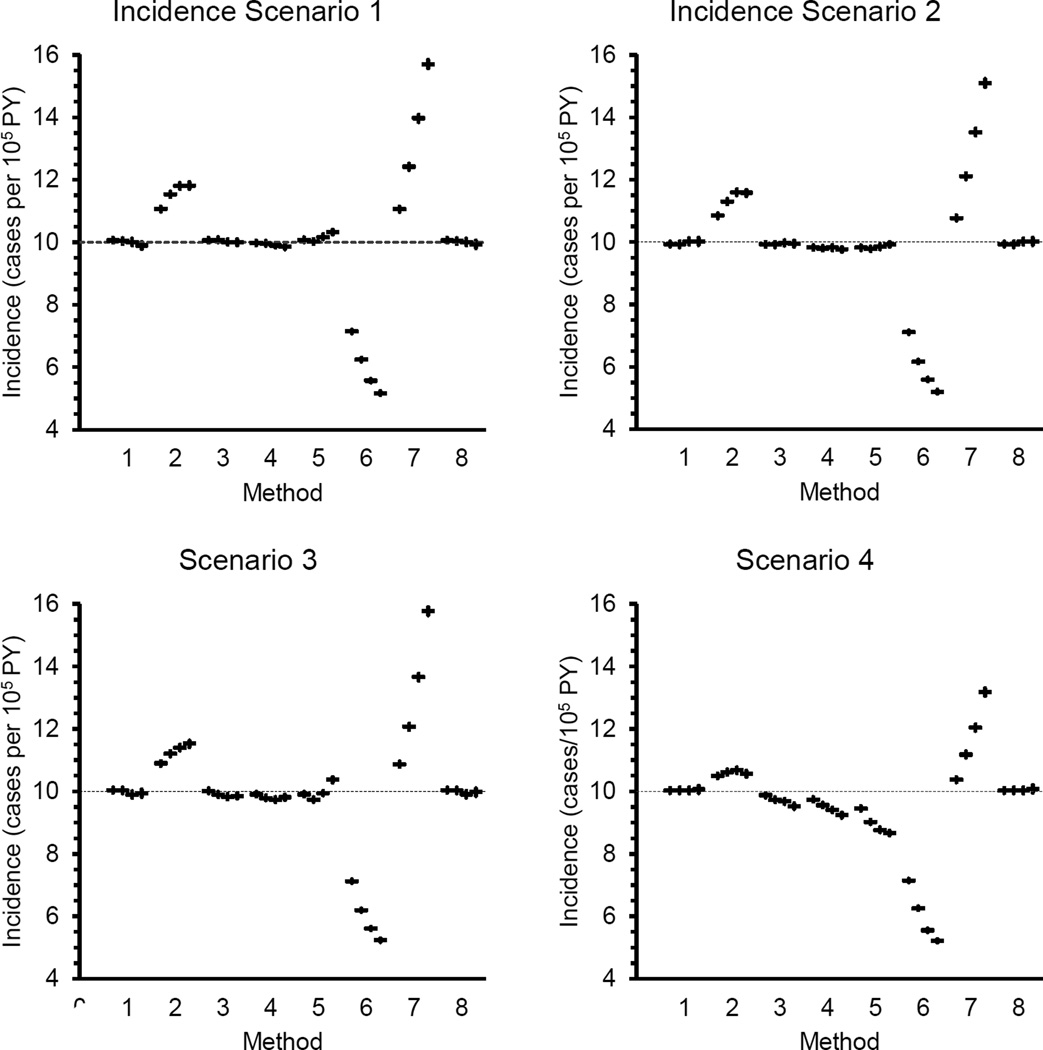
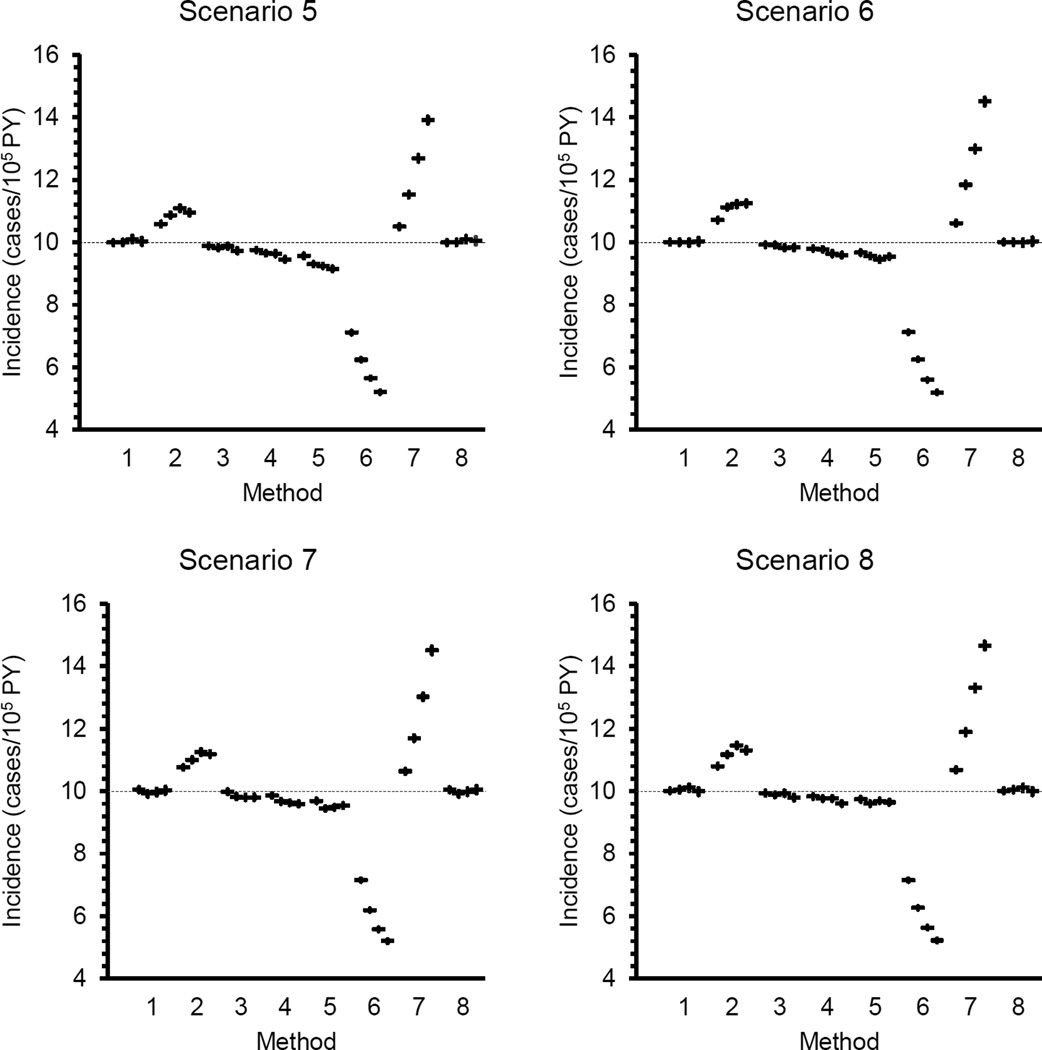
Estimates of average incidence with confidence limits are shown in Figure 2. More detailed information on the calculations, such as average follow-up time and number of cases in an estimate, is provided in a series of tables in the appendix. In general, the confidence intervals around mean estimated incidence (whether biased or unbiased) were no wider than ±0.15/10⁵PY, which is quite narrow when compared with the target value of 10/10⁵ PY.

Figure 2.

Mean estimated incidence with 95% confidence limits. Each set of four symbols represents mean incidence from one estimation method under the four donation frequencies defined in Table 2. The highest average donation frequency is on the left and the lowest on the right in each group of four.

When the incidence rate was constant over 8 years (incidence scenario 1), Methods 1, 3 and 8 produced approximately unbiased results under all mixes of donation history. Methods 4 and 5 produced approximately unbiased estimates at the two highest donation frequencies but Method 4 produced slightly negatively biased estimates and Method 5 produced slightly positively biased estimates with lower average donation frequency. Methods 2, 6 and 7 produced biased estimates under all conditions. Bias increased as average donation frequency declined. The modification to Method 7 to produce Method 8 eliminated the bias produced under the original Method 7 approach. In fact, Method 8 is mathematically equivalent to Method 1, which explains why the results from the two are identical.

Methods 1 and 8 also produced approximately unbiased estimates of incidence under Incidence Scenario 8, in which incidence rose prior to and during the estimation interval. Methods 2, 6 and 7 produced biased estimates under all donation frequency conditions, with bias increasing as donation frequency declined. Methods 3, 4 and 5 produced biased estimates under most but not all of the 32 test conditions. The modifications to Methods 1 and 3 had no effect on the results (data not shown).

The change in incidence was gradual in Scenarios 2 and 3 whereas in Scenario 4 the increase after Year 6 was both abrupt and large. Scenarios 5–7 were included to evaluate the effects of smaller changes in incidence at the end of Year 6 on incidence estimation. Only methods 1 and 8 produced approximately unbiased estimates under all combinations of donation frequency and incidence in years 1–6. Method 3 produced approximately unbiased estimates at the two highest donation frequencies when the incidence rate in years 1–6 was 7.5 or 8.75 cases/10⁵PY. Results from Method 3 were biased under all other conditions tested. Results from Methods 2, 4, 5, 6 and 7 were biased at all donation frequencies under Incidence Scenarios 5–7. The degree of bias varied with donation frequency and with the incidence rate assumed for Years 1–6.

As noted earlier, the donation inclusion criteria (i.e., the definition of a repeat donor who is informative for the incidence analysis) varied among approaches and, for Method 1 among studies in which this method has been used. Changing the inclusion criteria may dramatically alter the results from an estimation method. The difference between incidence estimates from Methods 5 and 6 illustrate this point. The algorithm for calculating incidence is the same under the two approaches but the criteria for selecting donors for inclusion in the incidence estimate differ, as do the estimates themselves. Method 7 consistently produced large positive biases when it was applied to a simulated group of donors with at least one donation in the estimation interval, as specified in the two studies in which it was used. However, it produced large negative biases when it was applied to simulated donors with at least two donations in the estimation interval (data not shown). Thus, the biases reported in this simulation study apply only when each of the methods is applied according to the repeat donor definitions described in the published reports.

The results reported here were based on a constant or average incidence rate of 10/10⁵ PY in the estimation interval. The simulations were repeated using incidence rates of 20/10⁵ PY and higher. The average incidence rates by the seven methods changed in proportion to the change in the underlying rate (data not shown). For example, the average incidence rates were approximately doubled when the underlying rate was increased to 20/10⁵ PY. Thus, the proportional biases in Methods 2–7 did not vary when the underlying rate changed.

DISCUSSION

All 7 methods included in this evaluation have been used in studies of the incidence of HIV infection in repeat blood donors. Methods 1–5 have also been used in studies of the incidence of Hepatitis C (HCV) infection.^{4,6–11,13–15} The results presented here should be applicable to both HIV and HCV. We have not evaluated the effects of the modifications used in studies of the incidence of Hepatitis B (HBV) infection.^{4,6–11,13–15} Therefore, we caution against extending the results to HBV.

Most of the methods included in this study produced biased estimates under some or all conditions included in this evaluation. Only Method 1, the so-called classical incidence window period method, and its mathematical equivalent, Method 8, produced approximately unbiased estimates under all conditions. We use the phrase approximately unbiased because simulations are not equivalent to the formal mathematical proof that an incidence estimate is unbiased. In fact we can go further, at least for Methods 1 and 8. An incidence estimate that is generated as cases over person-time using these two approaches is a maximum likelihood estimate of the parameter of an exponential distribution. Such an estimate is asymptotically unbiased, meaning that it is biased at small sample sizes and that the bias declines as sample size increases. Given the tight confidence limits around the means in our simulations, we can say that the sample size is large enough that any remaining bias in the estimates from Methods 1 and 8 is extremely small.

Methods 5, 6 and 7 were developed for use when the detailed information on donation history that goes into Method 1 is not available; however, all three methods are problematic. The results show that Method 7 is easily corrected. The corrected method (Method 8) can be applied in settings where an estimate of the average IDI can be obtained from a representative sample of donors. However, confidence limits on incidence calculated using the average IDI in a subsample of the donor population will be wider than the confidence limits based on the detailed information that goes into Method 1. Further work is required to determine if the approach to calculating the average IDI under Method 5 or 6 can be corrected to produce approximately unbiased estimates.

The confidence limits that are included in the results presented here should not be confused with the confidence limits around an estimate of incidence in a study of a group of blood donors. The confidence limits in this report reflect variability within each set of 4,000 incidence estimates, whereas the confidence limits around an incidence estimate in a study of blood donors reflect uncertainty about the true incidence rate in that population. The width of the confidence band around an incidence estimate depends on the number of cases in the numerator (i.e. the number of incident infections). One motivation for developing methods such as 2, 3 and 4 was to increase the number of cases in the numerator to reduce the width of the confidence band. The absence of bias in the results from Methods 1 and 8 has important implications for this effort. Any proportional change to the number of cases in the numerator must be accompanied by the same change in the denominator if the alternative method is to produce unbiased estimates. For example, a 20% increase in the number of cases must be matched by a 20% increase in time at risk. This requirement was not met by Method 2 or by Methods 5, 6 or 7 even when incidence was held constant over the entire 8 years of simulated donation history.

Why did Method 1 produce approximately unbiased estimates when Methods 2–4 failed to do so? Under Method 1, the data are treated as if they were obtained in a two-year longitudinal study. The first donation in the estimation interval is used to determine eligibility for the study. Infected donors are considered prevalent cases and are excluded, whereas uninfected donors are enrolled in the study at that point. Donors who remain uninfected through the last donation in the two-year interval are treated as right censored at the last donation. Follow-up for infected individuals is halted at the assumed point of infection. Under Method 1, three requirements are imposed on the data and estimation process: we require longitudinal information, which means that we need at least two donations by each donor, we only use donations made during the estimation interval and we use all donations in the interval up to the first one after the point of infection if infection occurs. The equation for incidence estimation reflects these requirements. Methods 2–4 invoke additional considerations vis a vis data inclusion by defining a maximum interval between observations and by allowing the use of data obtained before the estimation interval begins. Since neither of these modifications is built into the probability model for the data, they are not taken into account when incidence is estimated as cases/(person-time).. In other words, the process of imposing conditions on the data that are not reflected in the calculations can lead to biased estimates.

The results indicate that investigators should be very cautious about comparing estimates of TTI incidence in different studies. Any differences that are observed could be caused by the use of different estimation methods in addition to any real differences that may exist. Even if the same method is used, differences between incidence estimates may reflect underlying differences in donation frequency if any method other than Methods 1 and 8 was used.

Some of the biases identified in this evaluation are admittedly small or moderate in size. However, a small to moderate negative bias in one study coupled with a small to moderate positive bias in another can result in a larger apparent difference between estimates from the two. Comparisons of incidence estimates over time in the same population will also be affected by the selection of methods for incidence estimation. The difference between incidence estimates for two consecutive time intervals may be at least partially obscured if Method 2, 3 or 4 is used because each makes use of information prior to an estimation interval for donor selection of calculation of time at risk.

Our results have implications for evaluating the effects of changes in blood donor eligibility policy on TTI incidence in blood donors. Suppose, for example, that we wish to compare incidence rates after implementing a policy change with the incidence rate prior to the change. Only methods 1 and 8 are likely to provide entirely reliable information on the effect of changing policy across a wide range of infection rates and patterns of donation frequency.

In selecting an approach to evaluate the effects of a change in blood donation policy on HIV infection incidence or other source of variation in incidence, such as differences between populations, it is also important to consider the minimum size of the difference in incidence that would be of interest. If one is only interested in relatively large changes, then any method other than Methods 5, 6 or 7 may be suitable. However, if the issue is safety of the blood supply, it seems more likely that small to moderate differences will be of interest. This points to the need for careful selection of methods for incidence estimation in the evaluations. Accurate estimates are required for valid comparisons. For now, Method 1 is the best option for incidence estimation in repeat blood donors.