Benchmarking QM/MM Methods on the Thymidylate Synthase Catalyzed Hydride Transfer

Abstract

Given the ubiquity of hydride-transfer reactions in enzyme-catalyzed processes, identifying the appropriate computational method for evaluating such biological reactions is crucial to perform theoretical studies of these processes. In this paper, the hydride-transfer step catalyzed by thymidylate synthase (TSase) is studied by examining hybrid QM/MM potentials via multiple semiempirical methods and the M06-2X hybrid density functional. Calculations of protium and tritium transfer in these reactions across a range of temperatures allowed calculation of the temperature dependence of kinetic isotope effects (KIE). Dynamics and quantum-tunneling effects are revealed to have little effect on the reaction rate, but are significant in determining the KIEs and their temperature dependence. A good agreement with experiments is found, especially when computed for RM1/MM simulations. The small temperature dependence of quantum tunneling corrections and the quasiclassical contribution term cancel each other, while the recrossing transmission coefficient appears to be temperature-independent over the 5–40 °C interval.

Graphical Abstract

Introduction

The transfer of a light particle such as a proton, hydride or hydrogen atom is common in biological reactions. Nevertheless, prediction and interpretation of the associated macroscopic rate constant from computational simulations is far from straightforward due to the non-classical nature of the transferred particle. In this case, quantum tunneling effects and recrossing trajectories on the transition state (TS) dividing surface can be significant. Phenomenological models have proposed that specific protein fluctuations might reduce the donor–acceptor distances (DADs), thus diminishing the potential energy barrier height or/and width, and enhancing the rate constant by increasing the reactive trajectories over and through the barrier.^{1,2,3,4,5,6,7} Such models include environmentally-coupled tunneling,^1,2,3 promoting vibrations,⁴ vibrationally-enhanced ground-state tunneling,^5,6 and activated-tunneling models.⁷ However, a connection between such motions and the potential-energy barrier modulation has never been demonstrated directly. Additionally, analysis based on hybrid quantum mechanics/molecular mechanics (QM/MM) methods show the coupling of protein vibrations with the chemical subsystem in such a way that these vibrations could push the reacting system uphill along the energy barrier. Such methods may show the proteins’ vibrations contributing, if any, very modestly to the activation free-energy reduction.^{8,9,10,11,12,13,14,15,16} The use of isotopically-substituted enzymes,¹⁷ studies of mutants,¹⁸ and the study of KIEs and their temperature dependence have all been revealed as useful tools in testing the role of protein vibrations in enzyme-catalyzed reactions.^{8,19,20,21,22,23,24} In particular, the temperature-dependence of KIEs is associated with protein motions on the pico- to femtosecond timescale; these are coupled to the chemical step and may reduce the width and/or height of the potential energy barrier for that step along the chemical reaction coordinate.⁷

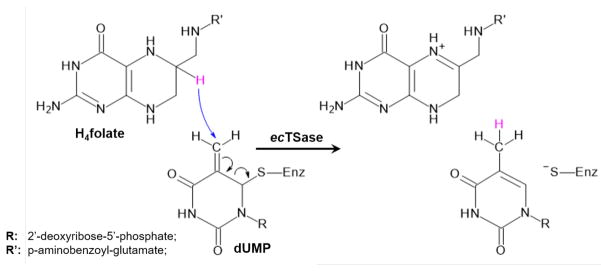
Thymidylate synthase (EC 2.1.1.45), TSase, catalyzes the reductive methylation of 2′-deoxyuridine 5′-monophosphate (dUMP) to 2′-deoxythymidine 5′-monophosphate (dTMP) by using N5,N10-methylene-5,6,7,8-tetrahydrofolate (CH₂H₄folate) as both methylene and hydride donor, producing 7,8-dihydrofolate (H₂folate).²⁵ Potential energy surfaces (PESs) of every single step of the cascade of chemical reactions catalyzed by TSase have been studied via QM/MM calculations.²⁶ The description of the molecular mechanism was in good agreement with the relevant experimental data,²⁵ confirming the rate-limiting step of the whole reaction as the reduction of an exocyclic methylene intermediate via hydride transfer from the H₄folate. The calculations also indicated that this step involves breaking the thioether bond between the C6 of dUMP and a conserved active-site cysteine residue (Cys146 in E. coli) concertedly with the hydride transfer from C6 of H₄folate to the dUMP intermediate (see Scheme 1).

Scheme 1.

Representation of the concerted hydride transfer and elimination of C146 step catalyzed by TSase.

There are experimental data suggesting that at 20–30°C, in the absence of Mg²⁺, the hydride transfer is essentially irreversible²⁵ and is rate-determining on both first-order (k_cat) and second-order rate constants (k_cat/K_m) for the overall reaction.^25–27 Further studies on this step, based on the exploration of free energy surfaces, have confirmed the concerted character of the hydride transfer and the elimination of the Cys146 step;²⁸ however, the results may have been biased if the sampling was insufficient, given the starting geometry in the molecular simulations.²⁹ The concern is this: since the generation of these free energy surfaces performed by molecular dynamics (MD) simulations at QM/MM level required extensive conformational sampling, the potential employed to describe the QM region was restricted to a semiempirical Hamiltonian, the AM1.³⁰ Consequently, the results are constrained by the inherent limitations of the selected QM method. A reliable description of the process depends critically on selection of an appropriate QM method.

Such a method has to be fast enough to explore the relevant conformations while properly describing the transformations taking place during the chemical reaction. Moreover, due to the nature of the particle being transferred, the evaluation of the rate constant by means of the conventional Transition State Theory (TST) presents serious deficiencies. Instead, more accurate results can be achieved by means of the variational Transition State Theory (VTST),^{31,32,33,34,35} which corrects the TST rate constant for (a) the trajectories that recross the TS dividing surface; and (b) the quantum tunneling effects derived from reactive trajectories that do not reach the classical threshold energy:^36,37,38

$$k_{\mathit{theor}}(T)=\mathrm{\Gamma }(T,\xi )\frac{k_{B}T}{h}exp\left(-\frac{\mathrm{\Delta }{G}_{\mathit{act}}^{QC}(T,\xi )}{RT}\right)$$ (1)

where R is the ideal gas constant, T is the temperature, k_B is the Boltzmann constant, h is Planck’s constant and $\mathrm{\Delta }{G}_{\mathit{act}}^{QC}$ is the quasiclassical activation free energy calculated along the reaction coordinate ξ:^33,39

$$\mathrm{\Delta }{G}_{\mathit{act}}^{QC}(T,\xi )=\mathrm{\Delta }{G}_{\mathit{act}}^{CM}(T,\xi )+\mathrm{\Delta }{G}_{\mathit{vib}}^{QM}(T)$$ (2)

In equation 2, the classical-mechanical (CM) activation free energy, $\mathrm{\Delta }{G}_{\mathit{act}}^{CM}(T,\xi )$, is obtained from the CM potential of mean force (PMF), W^CM(T, ξ), by means of the following equation:

$$\mathrm{\Delta }{G}_{\mathit{act}}^{CM}(T,\xi )=W^{CM}\left(T,\xi \right)-\left[W^{CM}\left(T,{\xi }_R\right)+G_{R,T,F}^{CM}\left(T\right)\right]$$ (3)

where ξ_R is the value of the reaction coordinate at the reactants (R) minimum of W^CM(T, ξ), and $G_{R,T,F}^{CM}\left(T\right)$ is the CM free energy of the normal mode (F) that corresponds to ξ equal to ξ_R. The value of W^CM (T, ξ_R) is usually assigned to be equal to 0. Then, the CM free energy barrier is $\mathrm{\Delta }{G}_{\mathit{act}}^{CM}\left(T,{\xi }_{\ast }^{CM}\right)$, where ${\xi }_{\ast }^{CM}$ is the value of the reaction coordinate corresponding to the maximum of W^CM(T, ξ). The last term of equation 2 corresponds to the correction term due to the quantized nature of molecular vibrations (mainly zero-point energies), $\mathrm{\Delta }{G}_{\mathit{vib}}^{QM}\left(T\right)$.^37,38,39,40

In equation 1, Γ(T, ξ) is the temperature-dependent transmission coefficient that contains the recrossing transmission coefficient, γ(T, ξ), and the tunneling corrections, κ(T), to the TST rate constant:

$$\mathrm{\Gamma }(T,\xi )=\gamma (T,\xi )\kappa (T)$$ (4)

In the present paper several combinations of potentials were selected to get the PMF of the reaction depicted in Scheme 1, as well as the tunneling and the recrossing transmission coefficients of equation 3. The selected potentials were two standard semiempirical methods, Austin Model 1 (AM1)³⁰ and PM3⁴¹, which are based on the NDDO Hamiltonian; the PDDG/PM3 Hamiltonian, which employs a pairwise distance-directed Gaussian modification that is added to the existing pairwise core repulsion functions within PM3;⁴² and the more recent reparameterization of the AM1 method, the Recife Model 1 (RM1).⁴³ The latter has been demonstrated to render good performance in a recent QM/MM study of the reduction of pyruvate into lactate catalyzed by lactate dehydrogenase (see scheme 2).⁴⁴ In addition, three other re-parametrized AM1 semiempirical methods were employed in order to show whether these sets of specific reaction parameters (SRP) were transferable to the hydride transfer reaction catalyzed by TSase. These methods were derived to reproduce higher-level calculations in the gas phase for the hydride-transfer reaction in formate dehydrogenase and dihydrofolate reductase (see Supporting Information).

Scheme 2.

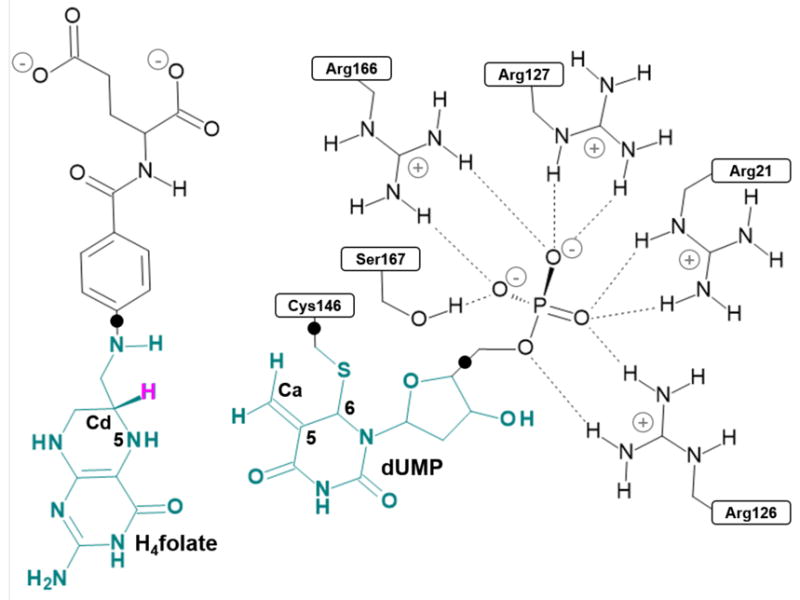
Schematic representation of the active site of the E. coli TSase prior to the hydride transfer step. Atoms in green are treated by QM methods. QM link atoms, depicted as black dots, were inserted in the QM-MM frontiers. The transferred hydride is highlighted in pink, and its donor and acceptor atoms marked as Cd and Ca, respectively.

The calculations, performed at four different temperatures for the transfer of protium and tritium, allow evaluation of the temperature dependence of the KIEs. The comparison of the different QM semiempirical methods with both the higher-level M06-2X⁴⁵ density functional theory (DFT) functional and with experimental data allowed us to choose a combination of potentials affording more reliable simulations of this key enzyme. The importance of performing a comparative analysis of methods has been stressed in a paper by Paasche et al.,⁴⁶ who tested the accuracy of various quantum chemical methods for the cysteine-histidine proton transfer reaction in the gas phase, as well as for mimicking a protease environment with implicit (continuum models) and explicit (QM/MM) methods. The analysis of our results also yields important information about the dynamics and quantum tunneling effects.

Computational Methodology

The model

The simulations started with the structure of Escherichia coli TSase bound to 5-fluoro-dUMP (FdUMP) and CH₂H₄folate (PDB code 1TSN)⁴⁷. The bacterial enzyme and the specific crystal structure were chosen for two reasons: first, in PDB code, 1TSN the inhibitor and cofactor are well-ordered and clearly display covalent links to each other and to Cys 146 in the active site. Thus, this is a very good X-ray structure to use as starting point in the study of the hydride transfer step. Second, the available experimental data for this specific TSase is the only set that directly examines the physical nature of the hydride transfer step at a level of detail that can be directly compared to calculations of that specific step.²⁵ In order to prepare the model for the simulations, the fluorine was replaced with a hydrogen atom at C5 of dUMP; the C-N bond between the methylene and N5 of H₂folate was broken; the proton from C5 of dUMP removed; and the exocyclic methylene was established (Scheme 2). Since the biological assemble of Escherichia coli TSase is a homodimer and the coordinates deposited in the 1TSN PDB refer only to a monomer, the homodimer was generated by symmetry replication with the help of the PDBePISA interactive interface.⁴⁸

The coordinates of the hydrogen atoms were added using the fDYNAMO⁴⁹ library after computing the pK_a values of ionisable amino acids with the empirical PROPKA3^50,51 program, in order to determine their proper protonation state in the protein environment.

A total of 25 counterions (Na⁺) were placed in optimal electrostatic positions (those where the potential reaches maximum negative values) around the enzyme (further than 10.5 Å from any atom of the system and 5 Å from any other counterion, using a regular grid of 0.5 Å) because the total charge of the system was not neutral. Finally, the system was solvated using a box of water molecules of 100 × 80 × 80 ų, and the water molecules with an oxygen atom lying within 2.8 Å of any heavy atom were removed.

The whole system was divided into a QM part and a MM part to perform combined QM/MM calculations. The QM part considers 25 atoms of the folate, 21 atoms of the dUMP and the side chain of Cys146, which gives a total of 54 QM atoms, and three hydrogen link atoms⁵² that were added at the boundary between QM and MM regions to satisfy the valence of the QM-MM frontier atoms (see Scheme 2). At this point, it is important to mention that although the quantum link atom in H₄folate is placed in a C-N polar bond (one usually tries to avoid cutting polar or unsaturated bonds), a test including the full H₄folate in the QM region (without this link atom) shows that no error is introduced with the partitioning presented in Scheme 2, probably because the link atom is placed more than 3 bonds away from the breaking C-H bond (see Supporting Information). The calculations modeled only one active site in the QM region, leaving the second active site (ligands removed) in the MM region. The MM part comprises the rest of the folate and dUMP, the enzyme, the crystallization and solvation water molecules, and the sodium counterions, which makes a total of 60826 atoms.

During the QM/MM energy optimizations and MD simulations, the atoms of the QM region were treated by the standard semiempirical methods AM1, PM3, PDDG/PM3, or RM1. Additionally, three different AM1 re-parametrizations, modified using specific reaction parameters (SRP) for FDH and DHFR hydride transfer catalyzed reactions and denoted as AM1-SRP,FDH,⁵³ AM1-SRP,DHFR⁵⁴ and AM1-SRP(D),DHFR⁵⁴ were used. The rest of the system, protein and water molecules, are described using the OPLS-AA⁵⁵ and TIP3P⁵⁶ force fields, respectively, as implemented in the fDYNAMO library.⁴⁹ Cut-offs for the non-bonding interactions are applied using a force-switching scheme within a range radius of 14.5 to 16 Å. Once the model was set up and minimized, an initial QM/MM MD simulation of the system in the NVT ensemble (with the QM region treated at AM1 level) was run using the Langevin-Verlet algorithm for 500 ps, using a time step of 1 fs at a temperature of 300 K. The structures had an energy fluctuation lower than 0.1%, a kinetic energy fluctuation lower than 1% and a change in temperature lower than 2.5 K over the last 2 ps of the MD. Moreover, according to the time-dependent evolution of the RMSD of those atoms belonging to the protein backbone, the system can be considered equilibrated (see Supporting Information).

Potential Energy Surface, PES

After setting up the model, steepest descent and conjugated gradient optimization algorithms were used until a gradient tolerance of 5 kJ·mol⁻¹ Å⁻¹ was met, followed by L-BFGS-B minimization steps until the completely optimized positions of hydrogen atoms were reached (gradient tolerance of 0.1 kJ·mol⁻¹ Å⁻¹). All atoms were then minimized, keeping all the residues further than 25 Å from the QM part frozen, due to the huge size of the system. The main interactions of the active site with the amino acids and crystallization water molecules were representative of the structure proposed by Stroud and Finer-Moore;⁵⁷ this may be considered an additional proof of the proper setup of the molecular model. The structure was then used to generate mono-dimensional (1D) and bi-dimensional (2D) QM/MM PESs for the rate-determining step of the TSase catalyzed reaction (Scheme 2). The selected reaction coordinate for generating the 1D PESs was the antisymmetric combination of the distances between the hydride donor and acceptor atoms, d(Cd-H) – d(H-Ca), while the distance between the C6 of dUMP and the sulfur atom of the Cys146 (dC6-S) was added as a second distinguished reaction coordinate to obtain the 2D PESs. Potential of Mean Force, PMF. All the PMFs were performed using structures from the previously obtained 1D and 2D PESs as starting points of each window. Although the generation of a PMF does not require structures to be extensively minimized, the use of optimized structures, equally spaced from reactants to products, as starting structures in the molecular dynamics simulations was found to be conducive to quickly getting converged results. Thus, mono-dimensional PMFs, or 1D PMFs, were computed using the antisymmetric combination of distances describing the hydride transfer as the distinguished reaction coordinate, as in the PES calculations. The weighted histogram analysis method (WHAM),⁵⁸ combined with the umbrella sampling approach,⁵⁹ was employed to scan the reaction coordinate in a range from −2.5 to 2.5 Å, with a window width of 0.05 Å, for a total of 101 windows . As in the case of the 2D PESs, the two-dimensional PMFs were obtained with the anti-symmetric combination of the distances describing both the breaking and forming bonds on the hydride transfer step and the distance between the C6 of the dUMP and the sulfur atom of the Cys146. A total of 61 simulations was performed at several values of d(Cd-H) – d(H-Ca), with an umbrella force constant of 2500 kJ·mol⁻¹·A⁻¹ for each particular value of the distance dC6-S (23 simulations with a force constant of 2500 kJ·mol⁻¹·A⁻¹, from 1.8 to 4.0 Å). All together, 1403 simulations were carried out.

The values of the variables sampled during the simulations were then pieced together to construct a full distribution function, from which the 1D-PMF and 2D-PMF were obtained. On each window, 10 ps of relaxation was followed by 20 ps of production with a time step of 0.5 fs (due to the nature of the chemical step involving a hydrogen transfer). The velocity Verlet algorithm was used to update the velocities in each window.

In order to improve the quality of the description of the QM sub-set of atoms in our QM/MM MD simulations, following the work of Truhlar et al.^60,61,62 a spline under tension⁶³ was used to interpolate this correction term at any value of the reaction coordinates ξ₁ and ξ₂ selected to generate the 2D PMFs. In this way we obtained a continuous function:^64,65,66

$$E\left({\xi }_1,{\xi }_2\right)=E_{LL/MM}+S\left[\mathrm{\Delta }{E}_{LL}^{HL}\left({\xi }_1,{\xi }_2\right)\right]$$ (5)

where S denotes a two-dimensional cubic spline function, and its argument is a correction term evaluated from the single-point energy difference between the high-level (HL) and the low-level (LL) calculation of the QM subsystem. In particular, S is adjusted to a grid of 23×61 points obtained as HL single energy calculation corrections. The various semiempirical methods were used as LL method, while M06-2X⁴⁵ hybrid functional, with the standard 6–31+G(d,p))basis set, was selected for the HL energy calculations. The functional and basis set were selected following the suggestions of Truhlar and co-workers^45,67 and based on our positive experience in previous studies on several different enzyme-catalyzed reactions. These calculations were carried out using the Gaussian09 program.⁶⁸

Recrossing transmission coefficients

In the present work, the recrossing transmission coefficient γ(T, ξ) is computed by means of the Grote-Hynes theory as the ratio between the reactive frequency (ω_r) and the equilibrium frequency (ω_eq), the frequency obtained under the assumption of equilibrium between the reaction coordinate and the remaining degrees of freedom of the system:⁶⁹

$$\gamma =\frac{{\gamma }_r}{{\gamma }_{eq}}$$ (6)

The equilibrium frequency is obtained by fitting the 1D PMFs, previously obtained, to a parabolic function:

$$\mathrm{\Delta }\mathit{PMF}=-\frac{1}{2}{k}_{eq}{\left(\xi -{\xi }^{TS}\right)}^2$$ (7)

where ΔPMF is the potential of mean force difference with respect to the maximum in the profile, k_eq is the equilibrium force constant, and ξ^TS is the reaction coordinate of the maximum of the profile. Therefore, the equilibrium frequency is:

$${\omega }_{eq}=\frac{1}{2\pi c}\sqrt{\frac{k_{eq}}{{\mu }_{\xi }}}$$ (8)

where μ_ξ is the reaction coordinate reduced mass and c is the speed of light.

The reactive frequency is obtained by applying the Grote-Hynes equation. Thus, once the equilibrium frequency is known, the reactive frequency can be easily obtained from the following relationship:^69,70

$${\omega }_r^2-{\omega }_{eq}^2+{\omega }_r\underset{0}{\overset{\infty }{\int }}{\zeta }_{TS}\left(t\right)e^{-{\omega }_{r}t}dt=0$$ (9)

The friction kernel (ζ^TS(t)) is obtained from the autocorrelation function of the forces exerted on the reaction coordinate when the system is constrained at the transition state:⁷⁰

$$\zeta \left(t\right)=\frac{\langle F_{\xi }\left(0\right)F_{\xi }\left(t\right)\rangle }{{\mu }_{\xi }{k}_{B}T}$$ (10)

where F_ξ (t) is the force on the reaction coordinate, k_B is the Boltzmann constant, T is the temperature, and ζ^TS(t) quantifies the coupling of the reaction coordinate with the rest of the degrees of freedom of the system.

Tunneling coefficient

Deviations from the conventional formulation of the TST as a result of quantum tunneling effects were estimated by means of the VTST. As shown in Equations 2 and 3, to correct the CM PMF, normal mode analyses were performed for the quantum region atoms. The zero-point energy for each mode was obtained by evaluating an ensemble average over primary subsystems and making a quasiharmonic approximation. At each ensemble point, we formed a Hessian and project the reaction coordinate. This allowed us to obtain the corresponding vibrational frequencies at each point along the reaction path, averaged over an ensemble that included the effects of anharmonicity. Quantization of the vibrational frequencies was then obtained as a correction to the CM PMF. In the reactants, zero-point energy was included in the reaction coordinate mode; at the TS, tunneling along the reaction coordinate mode was treated using the large curvature tunneling approximation. To perform these calculations, we localized 10 TS structures, starting from multiple configurations of the corresponding simulation windows in the heavy and light enzymes. After performing intrinsic reaction coordinate (IRC) calculations, we optimized the corresponding reactant structures and obtained the Hessian matrix for all of the stationary structures. The final quantum mechanical corrections were obtained as an average over these structures.

Kinetic Isotope Effects

KIEs were computed for isotopic substitutions of the hydride transfer from the TS and the reactant complex, localized at the levels of theory described above. The free energy of a state, G_i, can be expressed as a function of the molecular potential energy E_i, the total partition function Q_i, and the zero point vibrational energy, ZPE_i,

$$G_i=E_i-\mathit{RT}ln{Q}_i+{\mathit{ZPE}}_i$$ (11)

From Equation (11) and using TST, the ratio between the quasi-classical contribution to the rate constants corresponding to the light atom L and the heavier isotope H can be computed as:

$${\mathit{KIE}}^{QC}=\frac{{\left(\frac{Q_{TS}}{Q_R}\right)}_L}{{\left(\frac{Q_{TS}}{Q_R}\right)}_H}{e}^{-\frac{1}{RT}\left(\mathrm{\Delta }{\mathit{ZPE}}_L-\mathrm{\Delta }{\mathit{ZPE}}_H\right)}$$ (12)

In Equation (12), the total partition function, Q, was computed as the product of the translational, rotational and vibrational partition functions for the isotopologues at the reactant state and TS. The Born-Oppenheimer, rigid-rotor and harmonic oscillator approximations were considered in independently computing the different contributions. Keeping in mind that both of the states involved, reactants and TS, are confined to the active site of a protein, the contributions of translation and rotation to KIEs are negligible. Nevertheless, the full 3N × 3N Hessians were subjected to a projection procedure to eliminate translational and rotational components, giving rise to small non-zero frequencies, as previously described.⁷¹ Thus, it was assumed that the 3N - 6 vibrational degrees of freedom were separable from the substrate’s six translational and rotational degrees of freedom. KIEs were computed as averages of all possible combinations from 10 optimized structures of TS and 10 optimized structures of reactant state at the different combinations of semiempirical methods and classical force field, while M06-2X/MM values were computed from a single optimized structure of TS and reactants at this level of theory. The M06-2X/MM TS and reactants structures were located using as starting coordinates those previously located from the AM1/MM 1D-PMF generated at each temperature, and optimized by following an iterative micro-macro procedure.⁷²

According to equations 1 and 12, the total KIE can be expressed as the product of the quasi-classical contributions, the contribution from the recrossing transmission coefficient, and the contribution of the tunneling transmission coefficient:

$$\mathit{KIE}={\mathit{KIE}}^{QC}\times \frac{{\gamma }_L}{{\gamma }_H}\times \frac{{\kappa }_L}{{\kappa }_H}={\mathit{KIE}}^{QC}\times {\mathit{KIE}}^{\gamma }\times {\mathit{KIE}}^{\kappa }$$ (13)

RESULTS AND DISCUSSION

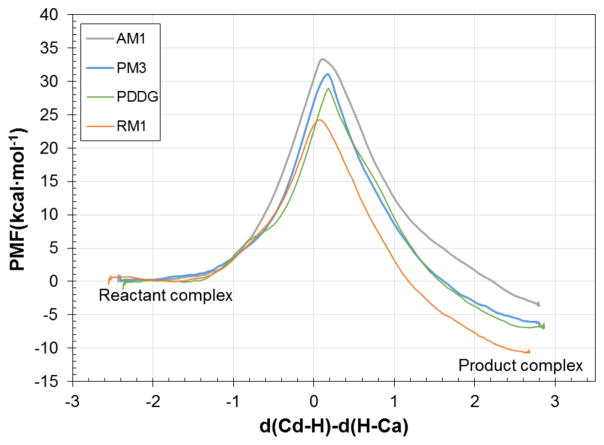
The first step in our study was to generate the free energy profiles for the hydride transfer of the TSase-catalyzed reaction along the antisymmetric combination of distances defining the breaking and forming bonds of the transferring hydride. This was done in terms of the classical mechanical PMF, W^CM. The resulting profiles, obtained at 293 K for all levels of theory mentioned in the previous section, are shown in Figure 1.

Figure 1.

QM/MM classical mechanical PMF, W^CM for the hydride-transfer step of the TSase catalyzed reaction, computed with various semiempirical methods, combined with the OPLS and TIP3P force fields, at 293 K. Distances of the reaction coordinate in Å.

The first conclusion that can be derived from the analysis of Figure 1 is that all methods describe the hydride transfer step as an exergonic process, although the reaction with the standard AM1 method is almost thermoneutral (−3.5 kcal·mol⁻¹). The results of the three SRP methods, reported in the Supporting Information, show that they are not transferable to the hydride transfer step catalyzed by TSase. The SRP,DHFR methods render endergonic results with noticeable high activation energies, while the SRP,FDH method fails in the rest of the computed variables, as shown in the Supporting Information. This result is not completely unexpected, considering that neither DHFR’s nor FDH’s hydride transfer takes place between the two moieties involved in the TSase reaction. Consequently, our study will be based on the use of the rest of the methods. AM1 resulted in the highest activation energy (33.3 kcal·mol⁻¹), while RM1 gives the lowest (24.2 kcal·mol⁻¹). PM3 and PDDG give energy barriers in between these two limits: 31.1 and 28.9 kcal·mol⁻¹, respectively. In addition, RM1 is the method that provides the highest stabilization of the product complex (−10.7 kcal·mol⁻¹).

Table 1 gives the average values of the key interatomic distances for the three states (reactants, TS and products) defined by the free energy profiles depicted on Figure 1. The first conclusion that can be derived is that all methods describe similar TSs: the anti-symmetric combination of the distances describing the breaking and forming of bonds in the hydride transfer step, d(Cd-H) – d(H-Ca), ranges from 0.27 Å, in the PM3/MM, to 0.37 Å in the AM1/MM.

Table 1.

Averaged interatomic distances for reactants, TS and products for the hydride transfer between H₄folate and dUMP. Distances are derived from the 1D-PMFs (computed at 293 K) displayed in Fig. 1 at different levels of theory. Optimized structures computed at M06-2X/MM level are also reported. All values are reported in Å.

d (Å)	RM1/MM	AM1/MM	PM3/MM	PDDG/MM	M06-2X/MM
	Reactants
d(Cd-H)	1.13 ± 0.03	1.14 ± 0.03	1.13 ± 0.04	1.13 ± 0.03	1.09
d(Ca-H)	2.82 ± 0.05	2.76 ± 0.04	2.93 ± 0.04	2.93 ± 0.04	2.25
d(Cd-Ca)	3.56 ± 0.14	3.65 ± 0.10	3.58 ± 0.13	3.68 ± 0.11	3.31
d(S-C6)	1.87 ± 0.05	1.91± 0.05	1.87 ± 0.04	1.85 ± 0.04	1.87
Transition State
d(Cd-H)	1.59 ± 0.03	1.63 ± 0.04	1.59 ± 0.04	1.58 ± 0.04	1.45
d(Ca-H)	1.23 ± 0.03	1.26 ± 0.03	1.32 ± 0.04	1.28 ± 0.03	1.26
d(Cd-Ca)	2.79 ± 0.06	2.87 ±0.07	2.88 ± 0.07	2.83 ± 0.06	2.70
d(S-C6)	1.96 ± 0.06	2.03 ± 0.07	1.93 ± 0.05	1.91 ± 0.05	1.92
Products
d(Cd-H)	3.69 ± 0.04	3.82 ± 0.05	3.81 ± 0.04	3.81 ± 0.04	3.67
d(Ca-H)	1.12 ± 0.03	1.13 ± 0.03	1.11 ± 0.03	1.11 ± 0.03	1.10
d(Cd-Ca)	4.66 ± 0.10	4.76 ± 0.09	4.78 ± 0.10	4.63 ± 0.17	3.75
d(S-C6)	2.01 ± 0.07	2.18 ± 0.11	1.96 ± 0.06	1.94 ± 0.05	1.98

The DAD, d(Cd-Ca), is reduced from reactant to the TS, indicating this distance as part of the real reaction coordinate. In the TSs, it ranges from 2.79 ± 0.06 Å (RM1/MM calculations) to 2.88 ± 0.07 Å (PM3/MM calculations). The distance of the C6-S bond in the TS ranges from 1.91 Å in the PDDG/MM to 2.03 Å in the AM1/MM, representing just a minor elongation by comparison with the value for the reactants complex. Importantly, all the methods describe the C6-S breaking bond in a very early stage of the process in product complex, ranging in distance from 1.94 ± 0.05 Å in PDDG/MM to 2.18 ± 0.08 Å in AM1/MM.

In an attempt to compare the performance of these semiempirical methods with a method based on a higher-level theory, the hybrid M06-2X functional was selected as a reference method. Due to computer limitations, a complete PMF could not be obtained at M06-2X/MM level. Consequently, a single TS structure was located at M06-2X/MM level, followed by an IRC traced down to reactants and products valleys. The key distances of the three involved states obtained at M06-2X/MM are included in Table 1. As can be seen, the values of the selected distances on the located TS were close to the average values obtained with the semiempirical methods and, in general, RM1/MM was the method providing the structures closest to the M06-2X/MM-optimized one. Thus, the DAD was 2.70 Å at M06-2X/MM level, while RM1/MM rendered 2.79 ± 0.07 Å. Regarding the S-C6 distance, RM1/MM gave a value of 1.96 ± 0.06 Å while M06-2X/MM gave 1.92 Å. In other words, from this analysis of the reactants and TS structures, it was not clear whether the hydride transfer and the S-C6 bond-breaking take place in a concerted manner.

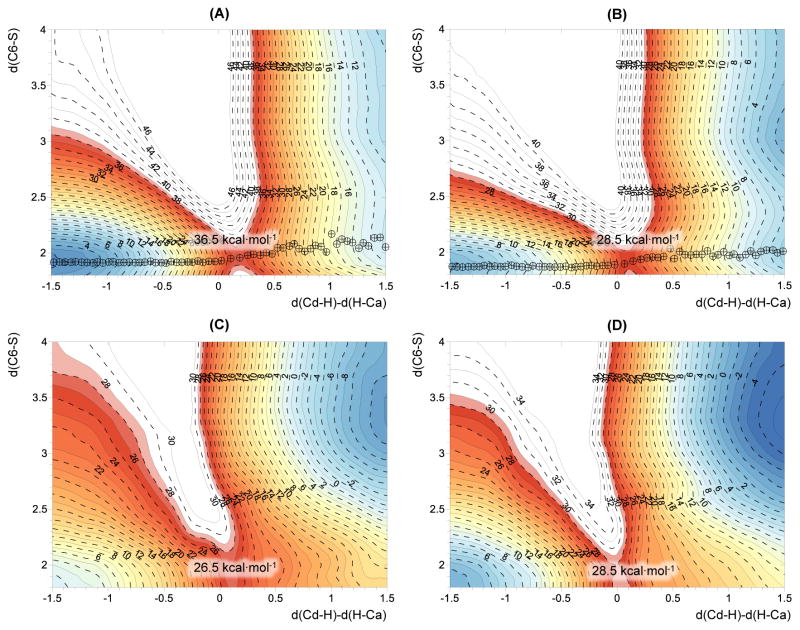
In order to check whether the hydride is transferred concertedly with the elimination of C146 and, more importantly, whether the TSs derived from the 1D-PMF represent the real TS of the reaction, 2D-PMFs were computed. These were generated as a function of the anti-symmetric combination of the distances describing the hydride transfer’s breaking and forming bonds, d(Cd–H) – d(H–Ca), and the distance between the C6 of the dUMP and the sulfur atom of the C146, d(C6–S). The calculations were done with the two standard semiempirical methods, AM1/MM and RM1/MM, used to render the limit values of activation and reaction free energies according to the 1D-PMFs reported in Figure 1. The resulting AM1/MM and RM1/MM free energy surfaces obtained at 303 K are shown in Figures 2A and 2B, respectively, while the corresponding corrected surfaces at M06-2X/MM level are shown in Figures 2C and 2D, respectively. Previous calculations of AM1/MM 2D PMFs computed in the same range of temperatures showed how the surfaces are equivalent, with no relevant changes in their topology.²⁸ Thus, the 2D-PMFs presented in Figure 2 show how the hydride transfer and the elimination of the C146 take place in a concerted but very asynchronous manner. This description is more evident when the free-energy surfaces are corrected at M06-2X/MM level (Figures 2C and 2D). Here, the products’ minima, corresponding to the breaking of the C6-S bond, appear more stable than they do in the original AM1/MM and RM1/MM surfaces (Figures 2A and 2B). In fact, shallow minima on the bottom right corner of Figures 2A and 2B (corresponding to an intermediate in which the hydride is fully transferred but the C6-S is not completely broken) can be detected, while they disappear after corrections in Figures 2C and 2D.

Figure 2.

2D-PMF computed at (A) AM1/MM; (B) RM1/MM; (C) AM1:M06-2X/MM; and (D) RM1:M06-2X/MM levels. Averaged values of the structures obtained along the corresponding 1D PMFs displayed in Fig. 1 are shown as circles in panels A and B. Distances of axes are in Å while values on isoenergetic lines are in kcal·mol⁻¹. Surfaces computed at 293 K.

From the energetic point of view, the quasiclassical activation free energy deduced from the 2D-PMF obtained at AM1/MM level appears clearly to be overestimated (36.5 kcal·mol⁻¹) by comparison with the RM1/MM value (28.5 kcal·mol⁻¹) and given the expected value derived from the experimental data. Interestingly, after corrections, the AM1/MM value is reduced to 26.5 kcal·mol⁻¹, while the M06-2X correction to the RM1/MM 2D-PMF is negligible, rendering the same value of 28.5 kcal·mol⁻¹.

The analysis of the values of the distinguished reaction coordinates at the TSs located on the quadratic region of the AM1/MM and RM1/MM free energy surfaces also produces interesting observations. The value of the anti-symmetric combination of the distances describing the breaking and forming of bonds in the hydride transfer step, d(Cd-H) – d(H-Ca), are 0.2 and 0.1 Å at the AM1/MM and RM1/MM TSs, respectively, while the distances between the C6 of the dUMP and the sulfur atom of the Cys146 (dC6-S) are 1.9 and 2.0 Å, respectively. The position of the TSs on the free energy surface thus indicates that the transferring hydride would be almost inbetween the donor and the acceptor atoms at the same time that the C6-S breaking bond is in a very early stage of the breaking process. This result is almost unaltered when the surfaces are corrected at M06-2X/MM level, as indicated by Figures 2C and 2D, which means that the description of the TS at semiempirical level, basically controlled by the hydride transfer, is adequate.

This description of the TSs is confirmed by the evolution of the re-hybridization state of the C6 atom from reactants to the TS, computed as previously proposed by Pu et al.⁷³ and based on the AM1/MM and RM1/MM structures selected from the reaction free energy path on the 2D-PMFs displayed in Figure 2. (See the evolution of the hybridization states of the C6 carbon atom in the Supporting Information.) Thus, the sp3 character of the C6 atom at reactants (characterized by a hybridization value close to 3) is almost unaltered at the TS (hybridization value of ca. 2.7 and 2.8 for the AM1/MM and RM1/MM calculations, respectively), while showing an sp2 character in products (hybridization value close to 2). These values, in agreement with previous calculations at AM1/MM level²⁹ and in accordance with measured 2° deuterium KIEs for the H6 position,⁷⁴ also suggest a small but measurable normal heavy atom KIE for ¹²C to ¹³C substitution at the C6.

In reference 74, the normal 2° KIE was interpreted as reflecting partial rehybridization from sp3 to sp2. In reality, the vibrational states of the 2° C6 hydrogen can be altered at the TS not only by rehybridization, but also by conjugation to the rest of the uracil ring system (especially to the C5=C4-O4⁻ moiety), which is dramatically altered from ground state to TS. Moreover, the TSs located on the 2D-PMFs computed at AM1/MM and RM1/MM level (Figure 2) are in agreement with the geometries deduced from the exploration of the free energy profiles computed as 1D-PMFs (Figure 1). Thus, although the structures of the product states obtained with the 1D-PMFs are different from the ones obtained from the 2D-PMF, the use of only the coordinates describing the hydride transfer appears to render a reasonable description of the region between the reactants and the TS, which is the area of the free energy surface that fundamentally dictates the kinetics of the reaction. This result is clearly shown when plotting the averaged values of the structures obtained along the 1D-PMFs on the 2D-PMFs displayed in Figure 2A and 2B. Essentially, the TS would be controlled by the hydride transfer and, notwithstanding the likelihood that C6 of dUMP might already have partly rehybridized toward sp2, the scission of the C6-S bond would take place after the hydride had been transferred. Then, further analysis are based on the TSs and reactants state located on the 1D-PMF.

Temperature-dependent KIEs

The next step in our study consists of computing the KIEs at 278 K, 293 K, 303 K and 313 K. As explained in the previous section, according to the VTST employed in the present study, KIEs can be evaluated as the product of three terms, the quasiclassical contribution, the contribution of the recrossing transmission coefficient, and the contribution of the quantum tunneling effects (see Equation 13). Thus, the PMFs for the hydride transfer are computed at the given temperatures, describing the QM subset of atoms with the four standard semiempirical methods. The results, reported in Table 2, reveal temperature-independent classical mechanical free energies of activation. All four methods show certain deviations with the change in the temperature, but no trend is observed through the examined temperature range.

Table 2.

Temperature dependence of the classical mechanical free energies of activation, W^CM, computed at different levels of theory. Values in kcal·mol⁻¹.

T (K)	RM1	AM1	PM3	PDDG
278	23.8	32.3	31.1	30.5
293	24.1	33.0	31.1	28.9
303	23.8	34.2	30.5	29.1
313	24.1	31.9	31.6	30.0

Transmission coefficient components due to the recrossing (γ) and tunneling effects (κ) were computed for the transfer of protium and tritium as described in the methods section. The results are presented in Table 3 and 4.

Table 3.

Temperature dependence of the recrossing transmission coefficient, γ, for the protium and tritium transfer computed at different levels of theory.

T(K)	AM1		RM1		PM3		PDDG
	H	3H	H	3H	H	3H	H	3H
278	0.62 ± 0.04	0.79 ± 0.07	0.57 ± 0.03	0.83 ± 0.08	0.33 ± 0.02	0.56 ± 0.03	0.47 ± 0.02	0.75 ± 0.05
293	0.55 ± 0.03	0.79 ± 0.07	0.53 ± 0.03	0.85 ± 0.08	0.21 ± 0.01	0.41 ± 0.02	0.34 ± 0.02	0.60 ± 0.03
303	0.53 ± 0.03	0.79 ± 0.07	0.60 ± 0.04	0.76 ± 0.06	0.31 ± 0.02	0.64 ± 0.04	0.46 ± 0.02	0.74 ± 0.04
313	0.56 ± 0.04	0.85 ± 0.08	0.58 ± 0.04	0.83 ± 0.08	0.16 ± 0.01	0.53 ± 0.03	0.47 ± 0.02	0.53 ± 0.03

Table 4.

Temperature dependence of the tunneling transmission coefficient, κ, for the protium and tritium transfer computed at different levels of theory.

T(K)	AM1		RM1		PM3		PDDG
	H	3H	H	3H	H	3H	H	3H
278	21.07 ± 3.71	10.50 ± 1.70	11.91 ± 2.27	8.23 ± 1.93	32.04 ± 10.51	14.32 ± 2.72	13.71 ± 0.99	9.11 ± 0.50
293	14.09 ± 2.20	8.09 ± 1.81	8.74 ± 1.46	6.63 ± 1.50	21.66 ± 6.08	10.55 ± 1.71	9.81 ± 0.56	7.21 ± 0.36
303	11.30 ± 1.63	6.98 ± 1.49	7.37 ± 1.14	5.86 ± 1.30	17.27 ± 4.39	8.86 ± 1.30	8.15 ± 0.41	6.31 ± 0.32
313	9.33 ± 1.25	6.13 ± 1.25	6.36 ± 0.91	5.26 ± 1.14	14.11 ± 3.25	7.60 ± 1.02	6.93 ± 0.31	5.61 ± 0.28

The results show no clear temperature dependence in the recrossing transmission coefficients. As observed in Table 3, the values for the transfer of protium are systematically smaller than those obtained for the tritium transfer, for all tested methods. This means that more recrossing trajectories are obtained when a lighter particle is transferred. It appears that the environment cannot respond and relax as quickly as the transfer takes place. In contrast, the tritium transfer is slower, giving more time for the environment to equilibrate, and resulting in fewer recrossing trajectories. This interpretation is confirmed by the equilibrium values and reactive frequencies computed for protium and tritium (see Supporting Information). Interestingly, apart from the PDDG, the rest of the methods render similar values, within the standard deviations uncertainty.⁷⁵ All in all, the contribution of these recrossing transmission coefficients, translated into an effective free energy of activation, ranges between 0.3 and 0.1 kcal·mol⁻¹.

In contrast to the free energy of activation and recrossing effects (Tables 2 and 3), the analysis of the quantum tunneling effects (Table 4) suggests a certain downtrend with the temperature for all tested methods. Thus, the tunneling effects are reduced with the temperature for all methods, which is in agreement with previous studies on hydride-transfer enzyme-catalyzed reactions.⁷⁶ In our previous study⁷⁷ carried out with the use of the AM1 semiempirical Hamiltonian and the CHARMMc22⁷⁸ force field to describe the protein, the values of the tunneling transmission coefficients were similar to the AM1/OPLS results reported in Table 4. Nevertheless, due to the high values of the standard deviations previously obtained, it was not possible to detect any clear temperature-related trend in the tunneling effects.⁷⁷ In the present study, as observed in the table, significant high values are obtained with the PM3 and PDDG methods, and especially with the SRP method, while slightly smaller values are obtained with the RM1 method. It is interesting to note that, although the standard deviations obtained for all methods are within the order of magnitude of previous studies, there are significant differences among methods. This can be attributed to the high dependency of the obtained tunneling transmission coefficient on the topology of the PES in the surroundings of the TS and, in turn, with the QM potential.

10 different conformations of structures selected from the windows of the maximum and the reactants minimum of the PMFs, which had been generated at the four temperatures, were selected and fully optimized as TSs and reactants state–like structures, respectively. These sets of structures were used to compute the quasi-classical primary tritium KIE, KIE^QC, as explained in the Methods section. In addition, the structures were optimized at M06-2X/MM level in order to get a high-level result, although this result is a single value, rather than an average over different conformations of reactants and TSs. The results are reported in Table 5.

Table 5.

Temperature dependence of the contribution of the quasi-classical primary tritium KIEs, KIE^QC, computed at different levels of theory.

T (K)	RM1	AM1	PM3	PDDG	M06-2X
278	5.87 ± 0.11	8.20 ± 0.13	7.42 ± 0.28	5.00 ± 0.13	8.27
293	5.44 ± 0.09	7.47 ± 0.11	6.89 ± 0.29	4.49 ± 0.45	8.40
303	5.16 ± 0.10	6.93 ± 0.22	5.92 ± 0.17	4.36 ± 0.33	7.85
313	4.95 ± 0.07	6.45 ± 0.17	5.81 ± 0.18	3.23 ± 0.31	7.67

According to the results, all methods provide similar values for the KIE^QC, although PDDG gives slightly lower values, especially at high temperatures. AM1/MM provides the values closest to the M06-2X calculations. Also, analysis of the data seems to show an inverse relationship between the magnitude of the KIE^QC and the temperature, although the variations in the full range of tested temperatures, 278 to 313 K, are not dramatic.

When computing the ratio between the recrossing coefficients obtained for the transfer of the protium and the tritium, listed in Table 4, its contribution to the KIE, KIEγ is quite similar for all methods, and no dependence on temperature can be detected (see Table 6).

Table 6.

Temperature dependence of the contribution of the recrossing transmission coefficients to the primary tritium KIEs, KIEγ, computed at different levels of theory.

T (K)	RM1	AM1	PM3	PDDG
278	0.69 ± 0.10	0.79 ± 0.12	0.59 ± 0.07	0.63 ± 0.07
293	0.62 ± 0.09	0.69 ± 0.11	0.52 ± 0.06	0.58 ± 0.06
303	0.79 ± 0.11	0.67 ± 0.10	0.49 ± 0.06	0.62 ± 0.06
313	0.70 ± 0.12	0.66 ± 0.11	0.30 ± 0.03	0.88 ± 0.10

Finally, the contribution of the quantum tunneling effects to the total KIEs was computed and is shown in Table 7. As observed, all values are quite similar and, most importantly, they follow the same trend as that detected for the tunneling recrossing coefficients that were computed for the protium and tritium (see Table 4): the higher the temperature, the smaller the contribution to the KIEs. As expected, it seems that the effect of tunneling in the KIEs diminishes with an increase in temperature. On closer inspection, the behavior of the different methods shows that the AM1/MM method gives the highest values while RM1/MM renders the lowest ones.

Table 7.

Temperature dependence of the quantum tunneling contribution to the primary tritium KIES, KIEκ, computed at eifferent levels of theory.

T (K)	RM1	AM1	PM3	PDDG
278	1.50 ± 0.23	2.05 ± 0.25	2.22 ± 0.45	1.51 ± 0.17
293	1.38 ± 0.20	1.78 ± 0.18	2.04 ± 0.35	1.36 ± 0.13
303	1.32 ± 0.19	1.65 ± 0.16	1.94 ± 0.30	1.29 ± 0.11
313	1.27 ± 0.18	1.55 ± 0.14	1.85 ± 0.26	1.24 ± 0.10

Once the three contributions to the KIEs were computed, the total KIEs could be estimated according to Equation 13. The results are listed in Table 8. The total primary tritium KIEs for the hydride transfer computed with the standard AM1, PM3, RM1 and PDDG are listed in Table 8A, while the values on Table 8B were obtained after computing the quasiclassical term, KIE^QC, at M06-2X/MM level.

Table 8.

Total primary tritium KIEs for hydride transfer with the QM part described at different semiempirical levels (A), and with correction of the quasi-classical KIE at the M06-2X/MM level of theory (B).

A
T (K)	AM1	RM1	PM3	PDDG
278	13.28 ± 0.50	6.08 ± 0.44	9.72 ± 0.80	4.76 ± 0.37
293	9.17 ± 0.40	4.65 ± 0.41	7.31 ± 0.70	3.54 ± 0.64
303	7.66 ± 0.48	5.38 ± 0.43	5.63 ± 0.53	3.49 ± 0.50
313	6.60 ± 0.42	4.40 ± 0.44	3.22 ± 0.47	3.52 ± 0.51

B
T (K)	M06-2X: AM1	M06-2X: RM1	M06-2X: PM3	M06-2X: PDDG	Exp.a
278	13.39 ± 0.33	8.56 ± 0.37	10.83 ± 0.52	7.87 ± 0.50	7.62 ± 0.4
293	10.32 ± 0.29	7.19 ± 0.29	8.91 ± 0.41	6.63 ± 0.19	6.91 ± 0.05
303	8.68 ± 0.30	8.19 ± 0.26	7.46 ± 0.36	6.28 ± 0.17	7.40 ± 0.55
313	7.85 ± 0.30	6.82 ± 0.25	4.26 ± 0.29	8.37 ± 0.20	7.12 ± 0.17

Experimental KIEs are obtained from reference 25

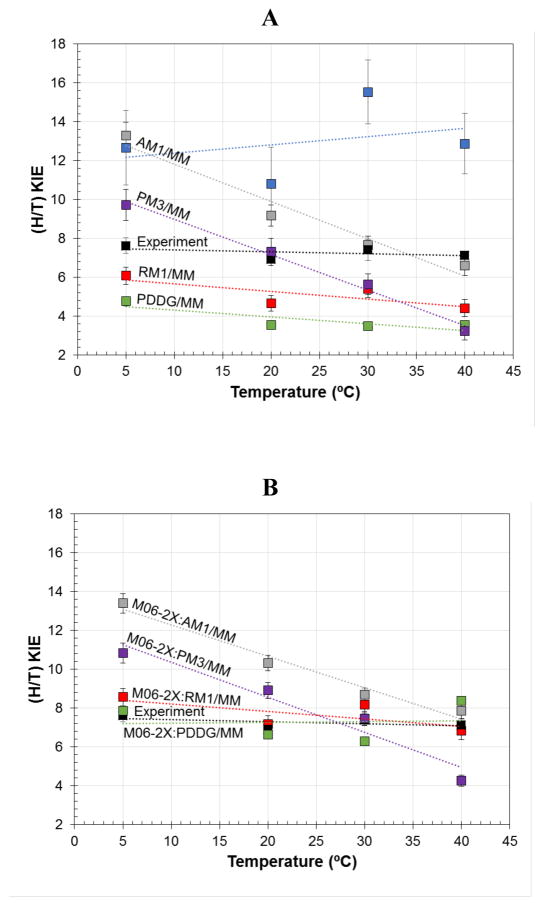
The first remark that can be made about the data listed in Table 8A is that there are significant differences among results obtained by the various methods. For instance, in comparison to the experimental data listed in Table 8B,²⁵ the AM1/MM method overestimates the KIEs; we noticed this in our previous studies performed with different MM force field.⁷⁷ On the other hand, RM1/MM, PDDG/MM and PM3/MM appear to underestimate KIEs. Another interesting result is that while AM1/MM and PM3/MM show the KIEs to be clearly temperature-dependent, this trend is much less obvious in the rest of the methods’ results. When computing the KIE at M06-2X/MM level (Table 8B), the RM1/MM and PDDG results coincide almost perfectly with the experimental data, while the results at AM1 and PM3 levels depart dramatically from the trend of the experimental data and may suggest temperature dependent KIEs. As observed in the data reported in the Supporting Information, the results obtained with AM1-SRP,FDH also deviates from the experimental data.

The comparison of the results is better appreciated through a graphical representation of the different sets of data. Figures 3A and 3B correspond to the data reported in Table 8A and 8B, respectively. Our experimental values²⁵ and our previous results⁷⁷ obtained at the AM1/CHARMMc22 level are also presented. The observations made above are clearly apparent in the figures: while the original AM1 and PM3 semiempirical methods indicate KIE temperature dependence, the two improved semiempirical methods, RM1 and PDDG, provide results that are in very good agreement with the trend of the experimental data. This agreement is almost at quantitative level when including the M06-2X/MM corrections (see Figure 3B).

Figure 3.

A) Temperature dependence of QM/MM KIEs obtained with five semiempirical methods: RM1 (red squares), AM1 (grey squares), PM3 (purple squares) and PDDG (green squares); and B) the corresponding values after correction at M06-2X DFT level. Experimental KIEs (from reference 25) are reported as black squares in both panels and previous theoretical results (from reference 77) as blue squares in panel A. Experimental errors and theoretical standard deviations are reported as bars on each point. Linear regressions on each set of data are presented for comparison purposes.

We then focused on the averaged structures of the maxima of the PMFs and, in particular, on the DAD distribution that was implicated as a possible origin of the variations in KIE temperature dependence. Temperature-independent KIEs would result from a very narrow distribution of DADs at the TS or, more specifically, at the region along the reaction coordinate called the tunneling ready state (TRS).⁷ The TRS was defined as the QM-delocalized TS, and represents all the DADs from which the particle is capable of tunneling. On the other hand, temperature-dependent KIEs indicate a loose active site in which the TS can attain a wide range of DADs at thermal equilibrium. At narrow distributions (high frequency of DAD sampling), a higher temperature does not populate higher vibrational states with shorter DADs. A broad distribution of TSs (low DAD-sampling frequency), however, yields a population of higher vibrational states at higher temperatures, meaning there is a higher probability of heavy-isotope transfer at higher temperatures, and thus smaller KIEs at higher temperatures. While the distribution of TSs determines the temperature dependence of KIEs, the size of the KIE reflects the average DAD. The results presented in Table 9 show no clear variation in this average distance with temperature, which would be in agreement with our previous computational study on this same enzyme,⁷⁷ but in contradiction to previous simulations on other enzymes such as DHFRs.⁷⁶

Table 9.

Temperature dependence of averaged DAD, Cd-Ca, at the TS computed at different Levels of theory. All values are reported in Å.

T (K)	RM1	AM1	PM3	PDDG
	Cd-Ca
278	2.72 ± 0.06	2.88 ± 0.07	2.86 ± 0.07	2.78 ± 0.06
293	2.79 ± 0.06	2.87 ± 0.07	2.88 ± 0.07	2.83 ± 0.06
303	2.80 ± 0.06	2.89 ± 0.07	2.83 ± 0.07	2.80 ± 0.07
313	2.80 ± 0.06	2.89 ± 0.07	2.84 ± 0.07	2.81 ± 0.07

CONCLUSIONS

This paper reports QM/MM studies of the hydride transfer step of the thymidylate synthase (TSase) catalyzed reaction, using different semiempirical methods to describe the QM sub-set of atoms. The main aim of the study was to determine the most appropriate semiempirical potential to be used in QM/MM calculations that require extensive sampling to get statistical properties. The selected potentials were the standard AM1, PM3, PDDG/PM3 and RM1, together with three SRP-reparametrized AM1 methods derived to reproduce the hydride-transfer reaction catalyzed by two related enzymes, DHFR and FDH. Calculations of protium and tritium transfer at four different temperatures allowed evaluation of the temperature dependence of the KIEs and comparison with experimental findings. The corresponding QM/MM free energy profiles were corrected with a DFT hybrid functional such as the M06-2X hybrid functional, and representative structures of the TS quadratic region of the free energy surfaces were compared with single TS structures located at M06-2X/MM level. The terms contributing to the total KIEs —the quasiclassical contribution, the recrossing effects and the quantum tunneling effects— were computed within the framework of the VTST. While the calculation of the last two terms used only semiempirical methods, due to the required hybrid QM/MM MD simulations, the quasiclassical term was computed at higher level of theory, using the M06-2X hybrid functional.

Based on the classical mechanical PMFs, two of the SRP tested methods (reparametrized to reproduce the hydride transfer in the DHFR) were excluded for further evaluations since they provided energies of activation that were too high and described the reaction as an endergonic process. This result is due to the fact that the hydride transfer in TSase is quite different than in DHFR. In DHFR the hydride is transferred from neutral species to a cation, while in TSase the accumulation of charges on the donor or acceptor carbons during the reaction depends on whether the N5 of the donor (H₄folate) loses a proton concertedly with the hydride transfer, as well as on whether the C6-S bond at the H-acceptor (dTMP) is cleaved concertedly with the hydride transfer. Indeed previous computational studies suggest that the hydride transfer in TSase takes place between two neutral species: proton transfer from TSase’s N5 takes place only after (a) the hydride transfer from H₄folate and (b) the covalent bond between the enzymatic nucleophile Cys146 and the pyrimidine dUMP (C6-S) has been cleaved.^26,28,29 The last SRP tested method, reparametrized to reproduce the hydride transfer in the FDH, was excluded since it failed when computing the recrossing transmission coefficients.

As for the remaining potentials, when the free energy surface was generated as a function of just the coordinates describing the hydride transfer, in terms of a mono-dimensional PMF, the C146 remained bound to the C6 atom of the dUMP in the products. In contrast, the two-dimensional PMFs described the reaction as a concerted but asynchronous mechanism in which the hydride transfer is conjugated to the cleavage of a covalent bond between a conserved cysteine and the dUMP. This result emerged more clearly when the surfaces were corrected at M06-2X/MM level. Nevertheless, the reaction deduced from these improved free energy surfaces appears to be so asynchronous that the TSs on the 1D-PMFs and the 2D-PMF turn out to be equivalent.

We turn to a comparison of the free energy surfaces computed using the AM1/MM and RM1/MM methods. RM1/MM 2D-PMF, by explicitly controlling the C6-S interatomic distance, gave a value coincident with the value obtained after correcting the surface at M06-2X/MM level. Results from this method showed that, given the evolution of the hybridization states of the C6 of dUMP, the TS is essentially controlled by the hydride transfer. Although the observation that C6 of dUMP has already partly rehybridized toward sp2, the scission of the C6-S bond clearly takes place after the TS of the hydride transfer. The rehybridization values at C6 state suggest a small but measurable normal heavy atom KIEs, computed for ¹²C to ¹³C substitution at the C6, and are in accordance with measured 2° KIEs, which are also affected by the vibrational state of the whole pyrimidine ring at the hydride TS.⁷⁴ Consequently, we were confident in further calculations and analysis of the free energy surface between reactants and TS based on the use of just the antisymmetric combination of distances defining the transfer of the hydride from folate to dUMP.

Recrossing transmission coefficients and quantum tunneling corrections were computed and, according to our results, the AM1, PM3, PDDG/PM3 and RM1 methods rendered similar values for the recrossing transmission coefficients, with the values obtained for the tritium slightly closer to unity than those obtained for the protium. This result is in agreement with a certain coupling between the hydride transfer and the changes in the protein, which is more significant in the case of a lighter particle. Nevertheless, the contribution of this effect to the activation energy would be lower than 0.3 kcal·mol⁻¹. Importantly, it appears that no method tested shows temperature dependence for recrossing transmission coefficients. Regarding the quantum tunneling effects, a small but measurable temperature dependence was obtained for all methods. Thus, the higher the temperature, the lower the tunneling contribution to the rate constant. This effect was not observed in previous calculations for the same reaction,⁷⁷ but could be due to the large standard deviations associated with the previous calculation. A similar trend was detected in a study of the hydride transfer in DHFR using similar methodologies.⁷⁶

AM1/MM and PM3/MM showed significant KIE temperature dependence as well as deviation from experimental values. However, RM1 and PDDG gave temperature-independent KIEs, qualitatively reproducing our experimental findings for this system.²⁵ This behavior appears to result from a cancellation of the opposite temperature-dependency effect on the tunneling coefficient and the quasiclassical term of the overall computed KIEs: while the tunneling contribution decreases with the temperature, the quasiclassical term increases. Moreover, when recalculating the quasiclassical contribution of the KIE with the M06-2X/MM method, an almost quantitative agreement with the experimental data was obtained.

The results reveal that the enzyme has tuned the H-transfer so that its KIEs are not sensitive to thermal population of the ensemble of DADs. Our results show that the observed fluctuations in the active site do not produce large deviations in this hydride’s DADs, thus enabling tunneling by both light and heavy isotopes of hydrogen. This finding accords well with phenomenological models that attempted to rationalize temperature independent KIEs in the context of narrow DAD distribution at the reaction’s tunneling-ready state.⁷ It can be concluded that in the case of thymidylate synthase-catalyzed hydride transfer, the recrossing and quasiclassical terms that contribute to the phenomenological free energies of activation appear to be temperature-independent, while the quantum tunneling corrections are slightly temperature-dependent. When the total KIEs are computed at M06-2X:RM1/MM or M06-2X:PDDG/MM level, they cancel out and a temperature-independent behavior is observed.

In previous theoretical studies on temperature dependence of the KIEs for the hydride transfer catalyzed by DHFR, two features were identified as reducing the temperature dependence by presenting opposite temperature-dependency trends:⁷⁶ the transition-state position and the effective potential barrier for tunneling. More enzymes catalyzing C-H→C hydride transfer will have to be studied before we know whether the different compensating features identified for DHFR and TSase are common or general in enzymology. The examination of different reactions would be also necessary to confirm the accuracy of QM methods and, in particular, the good performance of RM1 semiempirical method.