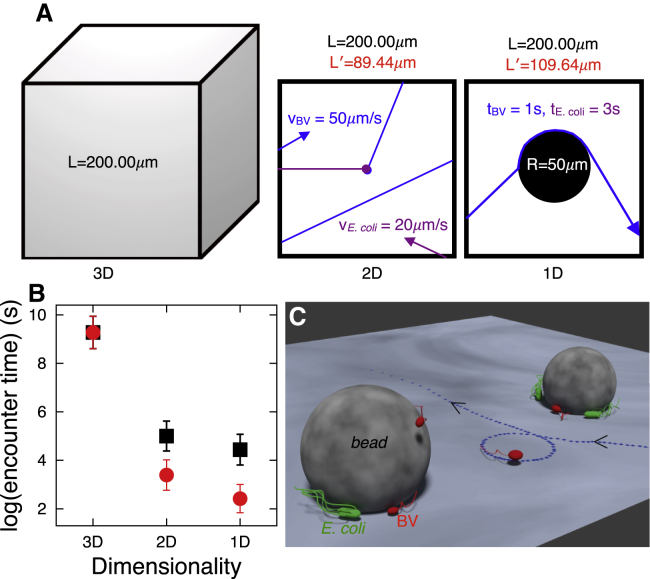
Figure 5.

Hydrodynamic interactions, passively, enhance encounter rates of the predator with the prey. (A) Here we illustrate how we calculate the encounter rates of the predator with the prey using our experimental results. A cube of length L = 200.00 μm is considered to simulate encounter rates in 3D (left), the area of a square of the same length for 2D (center), and to capture the motion along the boundary of the beads on the surface of the coverslip, a circle of radius R = 50 μm inside the same square for 1D (right). A pair of BV and E. coli—with radii r_BV = 0.50 μm and r_E.coli = 1.00 μm (approximated as spheres)—initially start at the center of the cube and square and select a random direction, then move in straight paths with speeds of v_BV = 50.00 μm/s and v_E.coli = 20.00 μm/s (from experimental data, Fig. 2 I), respectively. When any of them collide with the surface of the cube (3D) or edge of the square (2D and 1D), they start from a new random position with a new random direction on a new random side of the cube or square (all uniformly). In the 1D case, they initially start from an arbitrarily point outside of the circle, and when they encounter the circle, they move along its circumference—BV for 1.0 s (Fig. 3E) and E. coli for 3.0 s (averaged from 10 trajectories of E. coli along the bead surface on the coverslip) and then escape in a direction tangential to the circle. We record their positions at every 0.020 s (corresponding to a frame rate of 50 fps), and we consider a frame as an encounter time whenever the distance between BV and E. coli centers is less than r_BV + r_E.coli. We calculate encounter times from 1000 such collisions. (B) Natural logarithm of the encounter times (times between two successive encounters). (Black squares) Encounter times versus dimensionality without considering density enhancement (due to hydrodynamic effects); (red circles) corresponding times in the presence of the density enhancement. For red circles in 2D and 1D, we enhance the density fivefold to mimic density increases at surfaces due to hydrodynamics (Figs. 2K and 4B). We do so by reducing the length of the box from L = 200.00 μm to L′ = 89.44 μm (2D) and to L′ = 109.64 μm (1D). Error bars in (B) are 1 SD. (C) A qualitative illustration of geometric capture of predator and prey on surfaces and around beads as a result of their hydrodynamic interactions. To see this figure in color, go online.