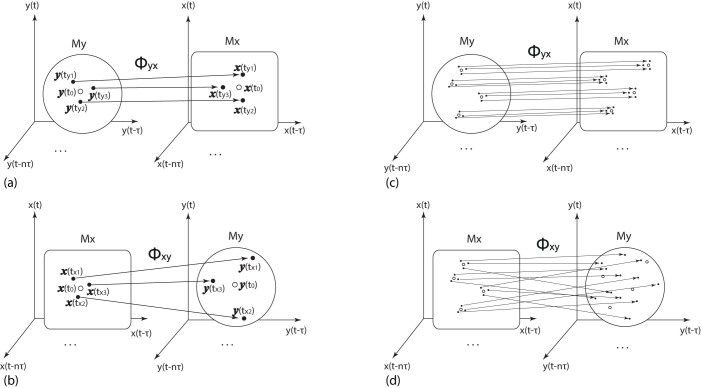
Figure 1. Illustration of mutual neighbors, cross map and smoothness.

(a) For one point y(t₀) ∈ M_y and its counterpart x(t₀) ∈ M_x, one can find the nearest neighbors , , 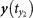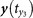for y(t₀) and define the mutual neighbors 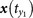, , 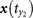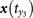for x(t₀). The map between the nearest neighbors and mutual neighbors is defined as cross map Φ_yx. In the case x causally influences y, the cross map Φ_yx maps a neighborhood to a neighborhood. (b) In the case y does not causally influence x, the cross map Φ_xy does not necessarily map a neighborhood to a neighborhood. (c) and (d) The global smoothness of Φ_yx and Φ_xy built from local smoothness.