Triode for Magnetic Flux Quanta

Abstract

In an electronic triode, the electron current emanating from the cathode is regulated by the electric potential on a grid between the cathode and the anode. Here we demonstrate a triode for single quantum magnetic field carriers, where the flow of individual magnetic vortices in a superconducting film is regulated by the magnetic potential of striae of soft magnetic strips deposited on the film surface. By rotating an applied in-plane field, the magnetic strip potential can be varied due to changes in the magnetic charges at the strip edges, allowing accelerated or retarded motion of magnetic vortices inside the superconductor. Scaling down our design and reducing the gap width between the magnetic stripes will enable controlled manipulation of individual vortices and creation of single flux quantum circuitry for novel high-speed low-power superconducting electronics.

Magnetic field in type II superconductors propagates in the form of Abrikosov vortices carrying single magnetic flux quanta¹. One could draw an analogy with single electrons, which carry electric current in microcircuits that are the basic building blocks of contemporary semiconductor electronics. The principle enabler of today’s microchips is the transistor (solid state version of the triode), where the flow of electrons is regulated by voltage or current in the base or gate electrode. Depending on the sign and value of the electrode voltage, the flow of electrons is accelerated or blocked, thus allowing signal amplification or ON/OFF switching that provides the 0 and 1 states in digital operations for memory devices and computer logic circuits.

In this work we propose a device consisting of a superconducting (SC) film with striae of soft ferromagnetic (FM) strips, which can be used to regulate the flow of magnetic flux quanta by varying the magnetic potential at the strip edges with the application of an in-plane magnetic field. The idea of exploiting the controlled motion of Abrikosov vortices for fast, low-dissipation memory devices has been considered for some time²,³,⁴,⁵,⁶,⁷ and was revived recently by the work of the Stockholm group⁸. The flux quantization of vortices in superconductors makes them a natural nanoscale information carrier for digital electronics, and in particular, for vortex based memories and microprocessors. However, this approach to novel electronics did not receive much traction due to the lack of reliable implements for controlling and manipulating vortices at the individual flux quantum level.

Here, we propose a technique to precisely manipulate vortices using a tailored FM/SC hybrid architecture, thereby providing a crucial step towards the development of an Abrikosov vortex circuit. There is a vast literature on the properties of the FM/SC hybrids describing interaction of vortices with different patterns of magnetic elements on top of superconducting films, as thoroughly reviewed in refs ^{9, 10, 11}. However, in the present work we consider an original design allowing new functionality that was not studied before. In this work, we used a few micron hybrid structures to allow optical imaging of the vortex dynamics. Nevertheless, the observed strong interactions of vortices with the magnetic strip edges will allow nano-scaling our designed features toward single vortex operation.

Results and Discussion

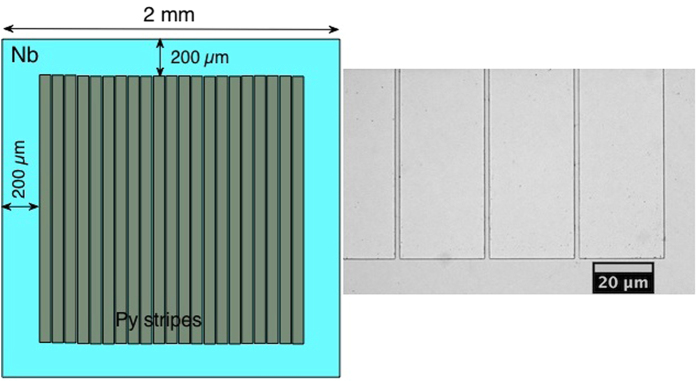
We studied the magnetic vortex motion in superconducting niobium (Nb) films overlayed with parallel thin strips of soft ferromagnetic permalloy (Py). The Nb film thickness was 100 nm (slightly above the London penetration depth of Nb, λ ~ 40 nm). The Py strips were 40 nm thick, 1.6 mm long, 30 μm wide and separated by 2 μm gaps. The strips possess in-plane magnetization with small anisotropy, which allows easy polarization along different in-plane directions. The striae of Py strips were lithographically patterned at the center of a 2 × 2 mm Nb square film, 200 μm from the square edges (Fig. 1).

Figure 1. Scheme of the sample.

2 × 2 mm 100 nm thick Nb film (blue) is covered in the center with an array of 30 μm wide and 40 nm thick parallel Py strips starting at 200 μm from the film edges. The gap between the strips is 2 μm as shown in the optical picture on the right.

A magneto-optical indicator film placed on top of the sample was used to image the normal magnetic flux component¹². The sample was cooled below the SC transition temperature (T_c = 8.7 K) in the presence of an in-plane magnetic field (H_X,Y) applied along a chosen direction with respect to the stripes. At temperature T < T_c, a field normal to the film surface (H_Z) was applied and gradually ramped up. Images of the penetrating normal flux, visualized as a bright contrast that is proportional to the vortex density generated by H_Z, were obtained using a cooled CCD camera and treated with image processing software. We subtracted the “zero-field” (H_Z = 0) images taken below T_c from the H_z ≠ 0 images to ensure that we visualized only the new vortices entering the Nb film with increasing H_Z and omit the alternating contrasts due to the stray fields of the magnetic Py strip edges.

At small enough H_Z, the Meissner screening current prevents the vortices from entering the Nb film and hence enhances the imaged normal field at the perimeter of the square sample. At larger fields, vortices enter the Nb film and form the so-called Bean state with the vortex density decreasing from the edges towards the interior of the film. With increasing H_Z, the vortex front advances closer to the boundaries of the magnetic Py strips.

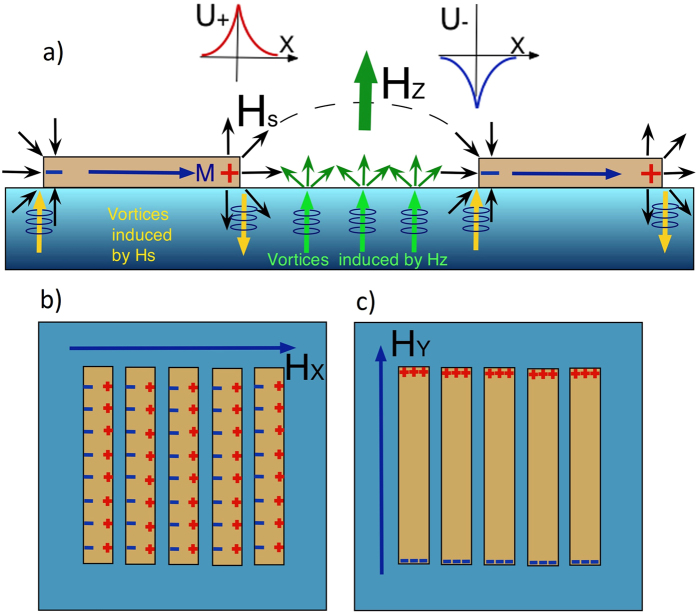
Upon reaching the Py strips, the vortex motion pattern is qualitatively changed. At this stage, the vortex behavior becomes strongly dependent on the magnetic polarization of the Py strips. When the strips are magnetized along their width (by the in-plane field H_X), effective positive and negative magnetic charges ( ρ_M = divM, where M is Py magnetization) appear at the long edges of the Py strips, and the sign of ρ_M alternates across the striae of Py strips as shown in Fig. 2a,b. For thin Py strips of thickness, d, with the in-plane magnetization polarized along their width, the long strip edges can be considered as lines of magnetic charge with charge density Md per unit length (Fig. 2b). In the gap space Δ = 2 μm between the Py strips, oppositely charged magnetic lines form linear dipoles (see Fig. 2a). However, for gaps much larger than the Py film thickness, Δ ≫ d, the charged lines at the long edges of the Py strips can be considered as solitary and the magnetic fields (H_S) emanating from these edges decay radially as the inverse distance from the edges.

Figure 2.

(a) Cartoon of stray fields (H_S) at the edges of Py stripes (brown) on top of the Nb film (blue). Vortices induced in the Nb film by H_S during the field-cooling (from T > T_C to T < T_C) are shown by yellow arrows and vortices induced by the field H_Z applied perpendicular to the Nb film at T < Tc are shown as green arrows. Distribution of magnetic charges for the in-plane polarization of Py stripes across (b) and along (c) their length (top view). For Hz induced vortices, the positively charged edges of the Py stripes act as lines of logarithmically diverging repelling potential barriers U₊ while along the negatively charged edges they become attractive potential valleys U₋.

Below the superconducting transition temperature, the stray fields, H_s, at and between the Py strip edges, may be only partially screened due to the Meissner effect induced in the Nb film, resulting in the creation of vortices in the film. For SC films thicker than the penetration depth λ, where total screening is achieved, the field acting on the superconductor from a linear magnetic charge along the y-axis (at r = x + iz) can be estimated as¹³:

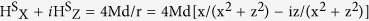This formula predicts the stray fields that exist only in the half space above the Nb film in the case of the superconducting screening and have twice larger amplitude than the fields H^s in the absence of the screening at T > T_c which are symmetric in the space above and below the Nb layer. Accounting for the large magnetization of Py (M ~ 800 G) there will be strong local stray fields near each Py strip edges. Upon cooling the sample below T_C, these stray fields will create positive vortices at the negative magnetically charged Py strip edges and negative vortices at the positive magnetically charged strip edges as indicated in Fig. 2a by the yellow arrows.

With the subsequent application of a normal field H_Z, new (positive) vortices will be generated (green arrows in Fig. 2a). These vortices will interact with the Py strip edges as magnetic monopoles carrying charge 2Φ₀/μ₀¹⁴. In turn, the Py strip edges will form lines of a local potential for vortices, U = ±∫2Φ₀H_sdx, decreasing logarithmically with distance x from the edge and with a lower cut-off range x₀ ~ λ. Furthermore, depending on the magnetic charge polarity, the potential can be either a barrier or an attractive potential well (Fig. 2a). In addition to this direct vortex/edge coupling, the entering vortices induced by H_z (H_z-vortices) will interact with the pre-existing vortices created during cooling in the stray field of the Py stripe edges (H_s-vortices). Near the positive magnetically charged Py strip edge, with the repulsive barrier towards positive H_z-vortices (U₊ in Fig. 2a), the stray-field induced vortices are negative (down yellow arrow in Fig. 2a). These negative H_s-vortices will attract the entering positive H_z-vortices (green arrow in Fig. 2a) and annihilate them. In contrast, the positive H_s-vortices at the negative magnetically charged Py strip edge, will repel the entering H_z-vortices, while the local potential at this Py edge is attractive for the H_z-vortices (U_- in Fig. 2a). Thus, the interaction between the entering H_z-vortices and stray field induced H_s-vortices is always opposite to the magnetic coupling of the H_z-vortices and the magnetically charged Py strip edges. However, as our experiments show (see below) the interactions of the H_z-vortices with the H_s-vortices turn out to be small and the coupling of the H_z-vortices with the charged stripe edges becomes the dominating factor in the vortex dynamics.

When the magnetic strips are polarized across their length (Fig. 2a,b), the local potential U at the strip gap consists of a linear barrier and linear valley along the opposing longitudinal strip edges (Fig. 2a). It contributes a substantial anisotropy to the vortex motion with preferential mobility along the linear potential, independent of the repulsive or attractive character of U. Indeed, we observe highly anisotropic deep penetration of vortices along the strip edges as shown in the magneto-optic image of the vortex field in Fig. 3a. This image confirms that in-plane polarization across the Py strip length induces channels for easy vortex entry along the strips. Such channels have a different nature compared to the channels of field-suppressed superconductivity formed e.g. due to the stray fields of domains at temperatures close to T_C¹⁵. In our low-temperature case (T ~ T_C/2), the main mechanism for channeling is the strong vortex motion anisotropy induced by the local linear potential landscape discussed above, rather than the suppression of superconductivity. The latter requires fields close to the upper critical field H_c2, while our values of Hs and Hz are well below H_c2 ~ 1.5 T at T ~ 5 K ¹⁶.

Figure 3. Magneto-optic images of the flux distribution for different polarization of Py strips in the sample at the same value of the normal filed Hz = 12.4 Oe applied below T_c at T = 5 K.

Pictures are taken near the bottom side of the sample. The edge of the Nb film is marked by short blue lines and the ends of the Py strips are marked by short red lines. The strips are polarized by field-cooling with an in-plane field of H_XY = 150 Oe applied in the directions shown by blue arrows. We checked that this in-plane field does not affect the motion of vortices induced by Hz using a control Nb film without Py strips. Sketches of magnetic charges in polarized Py strips for each direction of H_XY are shown next to the MO images and labeled by the same letters accented. Small MO pictures inserted in the sketches show distributions of the normal stray fields H^s at the stripe edges observed for corresponding directions of H_xy at T > Tc. In the larger MO pictures the MO patterns due to H^s are subtracted and they show only normal fields due to the vortices entering upon the application of H_z.

An intriguing situation emerges when the Py strips are polarized longitudinally. In this case magnetic charges appear at the short ends of the Py strips. They will be positive at one end and negative on the other (Fig. 2c). These charged strip ends create the same sharp attractive wells or repulsive barriers as noted above, but they are transverse to the motion of the H_Z induced vortices entering from the nearest Nb film sides. In this case, the gaps between the strips serve as narrow gates for vortex entry, although, even in the gaps, the vortex motion will be in part, impeded by the overlapping stray fields from the neighboring strip ends. As a result, vortices will enter much slower from the narrow Py strip ends than from the longitudinal sides of the strip pattern.

The maximum force of vortex/strip-end interactions is expected to have the same value ~|dU(x₀)/dx| for both + and − magnetic charge polarities at the strip ends. Surprisingly, it turns out that the effect on the motion of the H_z-vortices is quite different. The positively charged strip ends show a pronounced barrier action, preventing the motion of vortices (Fig. 3b). The enhanced bright color outside the positive magnetically charged Py stripe ends in Fig. 3b reveals a pileup of the H_z-vortices arriving from the Nb film edge. Dark triangles on the inner side of the Py strip ends correspond to the absence of vortices there. Some flux penetrates beyond the charged ends through the gaps between the strips and then expands symmetrically on both sides of the gap. Also, the amount of flux entering through the gaps is much smaller than in the case of cross-polarization of the strips (compare Fig. 3a,b taken with the same value of H_z).

In contrast to the positively charged magnetic strip ends, the attractive negatively charged ends are easily traversed by the entering H_z induced vortices as illustrated in Fig. 3c. There is a hardly visible small perturbation of the vortex density along the line of the negative strip ends in Fig. 3c.

Considering that entering H_z-vortices interact with both the magnetically charged Py strip ends and the associated magnetic stray-field induced vortices, and that these interactions compete with each other, the resulting effect should be defined by the dominant interaction. The strong vortex pileup at the positive Py strip ends in Fig. 3b confirms that here, the magnetic repulsion between the charged ends of the Py strip and the magnetic field of the H_Z vortices is the main factor. This could also explain the observed weak effect of the negatively charged Py strip ends. Here, the positive H_z-vortices are not retarded by the positive H_s-vortices but are accelerated towards the negative stripe ends and kinetically cross over the narrow attractive valleys U_-(x).

Finally, if the in-plane field is applied at π/4 from the long axis of the Py strips, we concurrently observe the combined effects of the cross and longitudinal polarized Py strips. i.e. the pile up of vortices at the ends of the strips and the channeling of vortices along the strip edges (Fig. 3d). In this case, magnetic charges are formed on all sides of the stripes (Fig. 3d’), such that one end and one long edge of the Py strip is charged positively and the other end and side have negative charge, resulting in the simultaneous pile-up and then channeling of vortices. Clearly the magnitude of both effects is different compared to the pure cross- or longitudinal polarization of the stripes.

The above experiments show that the cross polarization of the Py striae enhances vortex penetration, while longitudinal polarization can strongly suppress vortex entry. This array of thin magnetic strips with planar magnetization, which can easily be rotated with an in-plane field, acts as a grid for tuning the vortex motion. By turning the direction of the in-plane magnetic polarization of the Py strip with an in-plane magnetic field, it is possible to smoothly control the flow of vortex entry into the chosen area of the sample.

In summary, we have demonstrated that an array of parallel soft magnetic strips separated with narrow gaps is a unique structure allowing tunable manipulation of Abrikosov vortices in superconducting films. By rotating the magnetic moments of the Py strips, it is possible to switch from easy vortex channeling along the strip edges to strongly retarded flux entry between the strips. This is analogous to a magnetic triode operation, where a relatively small in-plane field can change the magnetic potential at the stripe edges allowing accurate control of the Abrikosov vortex motion. The action of the magnetic Py striae is similar to the work of a grid electrode regulating electron flow in electronic triodes. We envision that with appropriate miniaturization and choice of SC and soft FM components, our hybrid design can be used for developing superconducting single vortex circuits for digital and possibly quantum microprocessors, where high speed and low dissipating power are the leading requirements¹⁷,¹⁸.

Methods

The samples were prepared using 2-stage lithography technique. First, 2 × 2 mm Nb squares on silicon substrates were deposited by high vacuum DC magnetron sputtering onto a photoresist pattern manufactured using laser lithography. To inhibit proximity effects, after the lift-off process, the Nb squares were covered with ~15 nm SiO₂ film using plasma enhanced chemical vapor deposition system. Then the e-beam lithography was used to generate the patterns for 30 μm wide Py stripes with 2 μm gaps in the center of the Nb squares at 200 μm distance from the square edges. 40 nm thick Py film was deposited on top of the pattern followed by the lift-off. One of the Nb squares was left as a control sample.

The samples were placed on the cold finger of the optical closed-cycle cryostat ( Montana Instruments). They were covered with magneto-optical garnet indicator films and the normal component of the magnetic field in the samples producing the Faraday rotation of the light polarization in the film was imaged using a polarized light microscope⁹. Images of the flux patterns in the sample at different values of the normal field H_Z were recorded with 16 bit CCD camera. The field H_Z, was applied using a DC magnetic coil while the in-plane field H_XY was produced by a couple of permanent magnets that could rotate around the H_Z coil. The frame keeping the magnets allowed changing the distance between them and thus tuning the strength of H_XY. The orientation and value of the fields was controlled with a Hall probe.

In the experiment, the in-plane field of a chosen strength between 20 and 150 Oe was applied along, across, or at π/4 with respect to the Py stripes at T > T_C and was kept constant while the sample was cooled below T_C. This ensured a stable polarization of the Py stripes in the in-plane field direction. When the sample was cooled to a desired T (temperature stability ~10 mK) the normal field was applied and the flux distributions were recorded at increasing H_Z. By applying an in-plane field of 1 kOe to the control Nb square without Py stripes and imaging the penetration of the normal field H_Z at T < T_C we tested that H_XY up to 1 kOe does not affect the dynamics of H_Z vortices in our samples.

Additional Information

How to cite this article: Vlasko-Vlasov, V. K. et al. Triode for Magnetic Flux Quanta. Sci. Rep. 6, 36847; doi: 10.1038/srep36847 (2016).

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.