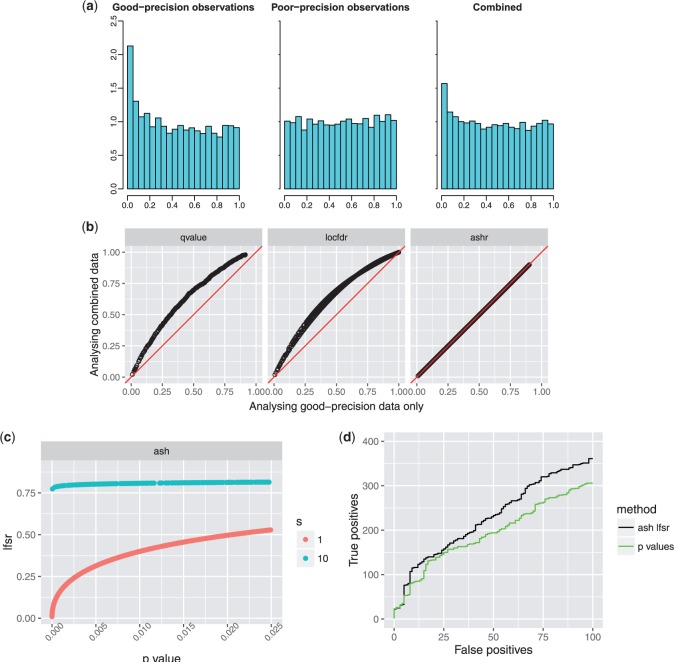
Fig. 4.
Simulations showing how, with existing methods, but not ash, poor-precision observations can contaminate signal from good-precision observations. (a) Density histograms of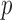 
values for good-precision, poor-precision, and combined observations. The combined data show less signal than the good-precision data, due to the contamination effect of the poor-precision measurements. (b) Results of different methods applied to good-precision observations only (
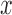-axis) and combined data (
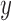-axis). Each point shows the “significance” (
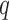values from qvalue; 
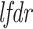for locfdr; 
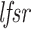for ash) of a good-precision observation under the two different analyses. For existing methods including the poor-precision observations reduces significance of good-precision observations, whereas for ash the poor-precision observations have little effect (because they have a very flat likelihood). (c) The relationship between 
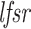and 
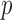-value is different for good-precision (
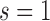) and low-precision (
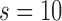) measurements: ash assigns the low-precision measurements a higher 
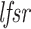, effectively downweighting them. (d) Trade-off between true positives (
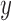) vs false positives (
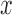) as the significance threshold (
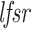or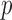 
value) is varied. By downweighting the low-precision observations ash re-orders the significance of observations, producing more true positives at a given number of false positives. It is important to note that this behaviour of ash depends on choice of 
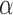. See Section 3.2.1 for discussion.