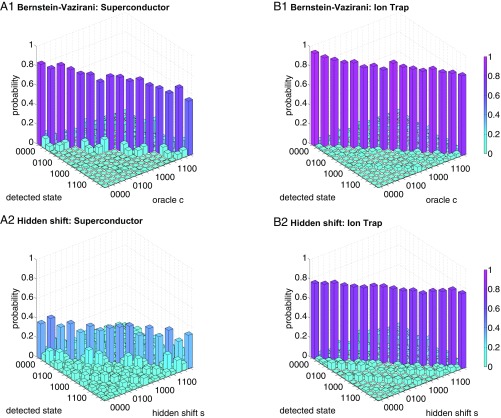
Fig. 4.

Results from the Bernstein–Vazirani algorithm implementing the oracle function $f_c(x)=x_0{c}_0\oplus c_1{x}_1\oplus c_2{x}_2\oplus c_3{x}_3$ for all possible $4$-bit oracles c performed on the star-shaped (A1) and the fully connected (B1) systems. The average success probabilities are $72.8(5)\%$ for the superconductor and $85.1(1)\%$ for the ion-trap system. The hidden shift algorithm for $f(x)=x_0{x}_1\oplus x_2{x}_3$. All possible $4$-bit shifted oracle functions are implemented on the superconducting system (A2) as well as the ion trap (B2). The average success probabilities are $35.1(6)$% and $77.1(2)\%$, respectively. The axes represent states and oracle parameters as $4$-bit binary numbers.