An Automated Reference Frame Selection (ARFS) Algorithm for Cone Imaging with Adaptive Optics Scanning Light Ophthalmoscopy

Abstract

Purpose

To develop an automated reference frame selection (ARFS) algorithm to replace the subjective approach of manually selecting reference frames for processing adaptive optics scanning light ophthalmoscope (AOSLO) videos of cone photoreceptors.

Methods

Relative distortion was measured within individual frames before conducting image-based motion tracking and sorting of frames into distinct spatial clusters. AOSLO images from nine healthy subjects were processed using ARFS and human-derived reference frames, then aligned to undistorted AO-flood images by nonlinear registration and the registration transformations were compared. The frequency at which humans selected reference frames that were rejected by ARFS was calculated in 35 datasets from healthy subjects, and subjects with achromatopsia, albinism, or retinitis pigmentosa. The level of distortion in this set of human-derived reference frames was assessed.

Results

The average transformation vector magnitude required for registration of AOSLO images to AO-flood images was significantly reduced from 3.33 ± 1.61 pixels when using manual reference frame selection to 2.75 ± 1.60 pixels (mean ± SD) when using ARFS (P = 0.0016). Between 5.16% and 39.22% of human-derived frames were rejected by ARFS. Only 2.71% to 7.73% of human-derived frames were ranked in the top 5% of least distorted frames.

Conclusion

ARFS outperforms expert observers in selecting minimally distorted reference frames in AOSLO image sequences. The low success rate in human frame choice illustrates the difficulty in subjectively assessing image distortion.

Translational Relevance

Manual reference frame selection represented a significant barrier to a fully automated image-processing pipeline (including montaging, cone identification, and metric extraction). The approach presented here will aid in the clinical translation of AOSLO imaging.

Introduction

The application of adaptive optics (AO) to ophthalmoscopes has revolutionized vision research by allowing diffraction-limited imaging of the living retina. AO flood-illuminated ophthalmoscopy (AO-flood),¹ AO scanning light ophthalmoscopy (AOSLO),^2,3 AO-line scanning ophthalmoscopy (AO-LSO),⁴ and AO-optical coherence tomography (AO-OCT)^5–7 are used by basic scientists and clinical researchers to examine healthy^8–14 and diseased retinas.^15–21 Confocal AOSLO is commonly used to visualize wave-guided light from cone and rod photoreceptors,²² and multiply scattered, nonconfocal reflected light may be split and recombined to visualize photoreceptor inner segments,²³ the retinal pigment epithelium,²⁴ or retinal ganglion cells.²⁵ These techniques have led to strategies for informing candidacy for human gene therapies^19,23,26,27 and offer a new avenue in studying mechanisms underlying retinal health in animal models.^28–36

While much of the focus in advancing AO technology has been on hardware,³⁷ the rate-limiting step in applying AO more broadly to clinical settings is often the processing and analysis of the images. Without an efficient processing pipeline, AO ophthalmoscopes are impractical for clinical use due to the significant effort currently required for processing and analysis. Advances have been made in automatic montaging of images of the cone photoreceptor mosaic^4,10,38 and identification of individual cones,^{4,10,12,39–42} yet software for processing the raw image sets is still lacking. Due to involuntary eye motion and the relatively low signal from retinal reflectance, AO image sequences must be registered to a reference frame and averaged to increase the signal-to-noise ratio (SNR).^43–48 Reference frame selection traditionally requires expert manual oversight,^{4,44,46,47,49} which is subjective and time consuming. This process typically involves estimating the overall eye motion within an image sequence so that the reference frame will have a significant overlapping area with other frames (hereby, referred to as being spatially representative), and closely examining features between frames to detect subtle expansions and compressions that result from over- or under-sampling regions of the retina during tremor and drift.^45,50 Frequently, humans may select multiple reference frames within a video that appear to be spatially segregated in order to increase coverage of the retinal area. This approach aids the montaging step where processed images from different retinal locations are stitched together to form a large composite image of the retina.

Algorithms that employ template-independent image quality metrics (e.g., sharpness, contrast, brightness) or statistical methods for automated reference frame selection from AO-flood,^51–53 AO-LSO,⁴⁰ and AO-telescopes⁵⁴ have been proposed; however, these metrics are not robust for detecting motion artifacts within AOSLO images. Unsupervised registration algorithms of raw AO-flood image sequences have been developed,^55,56 however their efficacy in handling large motion artifacts has not been demonstrated. Acquisition and postprocessing schemes have been developed for OCT and AO-OCT to correct for involuntary eye motion, but still require manual selection of a registration template,^49,57,58 or require orthogonal raster scanning,⁵⁹ which has not been implemented in AOSLO. Real-time eye tracking combined with AOSLO has been reported,⁶⁰ which would enable automated reference frame selection through image analysis if motion artifacts were eliminated. However, even with optical and digital image stabilization, motion artifacts persist in a significant portion of frames and could benefit from an automated method of selecting minimally distorted reference frames.

Here, we sought to develop an automated reference frame selection (ARFS) algorithm optimized for our primary imaging modality: confocal AOSLO of the photoreceptor mosaic. Our algorithm comprises two main modules: distortion detection to select the least distorted frame(s) from an image sequence and motion tracking to allow selection of multiple reference frames from distinct spatial locations to potentially increase coverage and aid in the creation of montages. We compared the level of residual distortion in images processed by ARFS and one expert human observer (RFC), assessed the accuracy of motion tracking, and determined how frequently a group of human observers select one of the least distorted frames in a sequence identified by ARFS. ARFS may reduce the data backlog inherent in AO imaging and allow researchers and clinicians to focus on analyzing⁶¹ and interpreting⁶² AO images of the retina.

Methods

Image Sequences

Image sequences were obtained using previously described AOSLO^22,50 and AO-flood systems.⁵⁰ The AO-flood had an exposure time of 6 ms, and the AOSLO had frame rate of 16.6 Hz with a line rate of approximately 15 kHz. Static sinusoidal distortion resulting from use of a resonant scanner was corrected in AOSLO images.^2,3 To determine the planar scale of retinal images in micrometers per pixel, images of a Ronchi ruling were acquired at the focal plane of a 19-mm focal length lens, and an adjusted axial length method⁶³ was used to estimate the retinal magnification factor based on the subjects' axial length measurements obtained via IOL Master (Carl Zeiss Meditec, Dublin, CA). AO-flood images were upsampled with bicubic interpolation to match the scale of the corresponding AOSLO images using Photoshop CS6 (Adobe, San Jose, CA). This study followed the tenets of the Declaration of Helsinki and was approved by the institutional review board at the Medical College of Wisconsin.

Algorithm Workflow

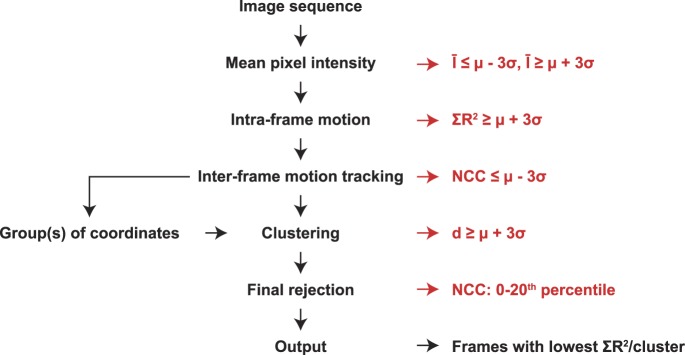
This algorithm was implemented in Matlab (MathWorks, Inc., Natick, MA) and proceeded as follows (Fig. 1). First, to eliminate frames that were either saturated or acquired during blinks, frames were kept only if their mean pixel intensity (Ī) was not an outlier (μ − 3σ ≤ Ī ≤ μ + 3σ), where μ and σ are the average and SD of a given metric for the sequence, respectively. To eliminate frames with large motion artifacts and measure intraframe distortion (full description following; Fig. 2), coefficients of determination (R²) obtained from linear regression of the processed discrete Fourier transform (DFT) of frame strips were summed (ΣR²), and outliers were rejected (ΣR² ≥ μ + 3σ). To identify spatially segregated clusters of frames, motion tracking (Fig. 3) and clustering (Fig. 4) were conducted and outliers were rejected by the following metrics: normalized cross-correlation (NCC) peak height: (NCC ≤ μ − 3σ), and distance (d) to cluster centroid (d ≥ μ + 3σ). NCC peak heights are reduced by intraframe distortion, so we conducted an additional “strict” rejection by removing frames with the lowest 20% of NCC peak heights. The frames from each distinct spatial cluster with the lowest ΣR² values from the intraframe motion module were then output to the user for use in their preferred method of registration and combination. Also, output to the user was the relative coordinates of each frame, cluster assignment, and number of frames in each cluster to inform the registration process. Many parameters are currently hard-coded, and should be tuned to the user's dataset; a list of parameters with tuning suggestions is given in Supplementary Table S1.

Figure 1.

Algorithm workflow. Frames from an AOSLO image sequence were rejected using the conventional definition of an outlier as an observation being at least 3 SDs (σ) away from the mean (μ). They were rejected based on mean pixel intensity (Ī ≤ μ − 3σ or Ī ≥ μ + 3σ), intraframe motion (ΣR² ≥ μ + 3σ), NCC peak height (NCC ≤ μ − 3σ) after motion tracking, and distance to cluster centroid (d ≥ μ + 3σ) after clustering. An additional “strict” rejection was conducted by removing frames with the lowest 20% of NCC peak heights. The frames from each distinct spatial cluster with the lowest ΣR² values were output.

Figure 2.

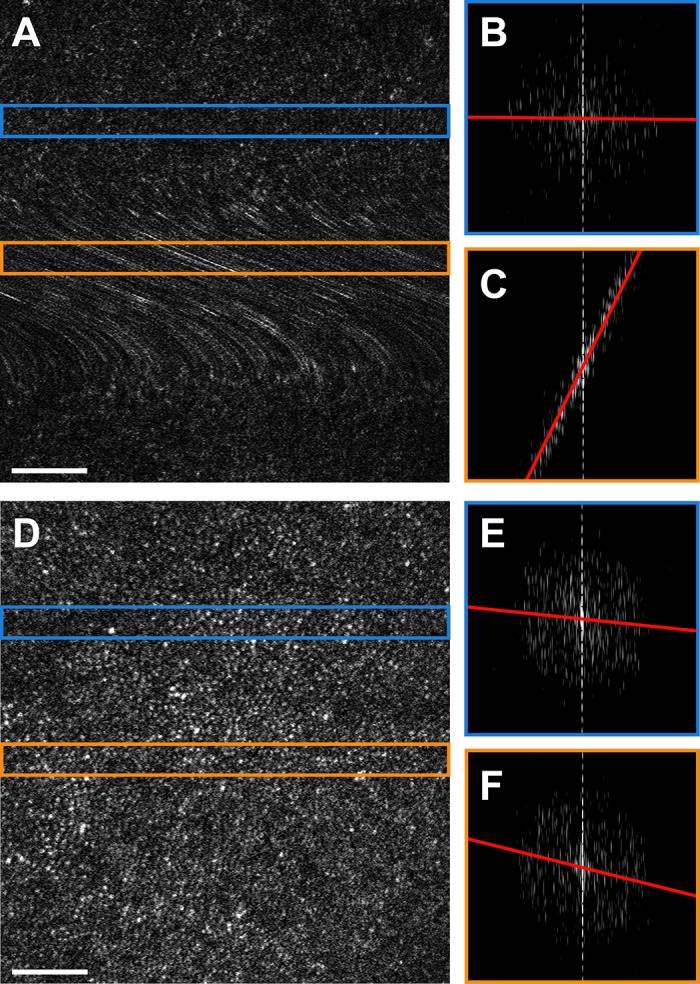
Intraframe motion process. (A) Raw AOSLO frame exhibiting both a normal cone mosaic and a prominent motion artifact resulting in blurring of the photoreceptors. (B) Log₁₀-scale image of the DFT calculated from the strip outlined in blue from (A). The red line indicates the least-squares linear regression of the maxima across columns, with an R² value of 0.0085. (C) Log₁₀-scale image of the DFT calculated from the strip outlined in orange from (A). The R² value of this regression is 0.98, suggesting a significant distortion. (D) Raw AOSLO frame exhibiting no obvious distortions. (E) Log₁₀-scale image of the DFT calculated from the strip outlined in blue from (D), R² = 0.011. (F) Log₁₀-scale image of the DFT calculated from the strip outlined in orange from (D), R² = 0.046, possibly suggesting a subtle distortion, but could also be within the normal limits of variability for this frame. Scale bars, 50 μm.

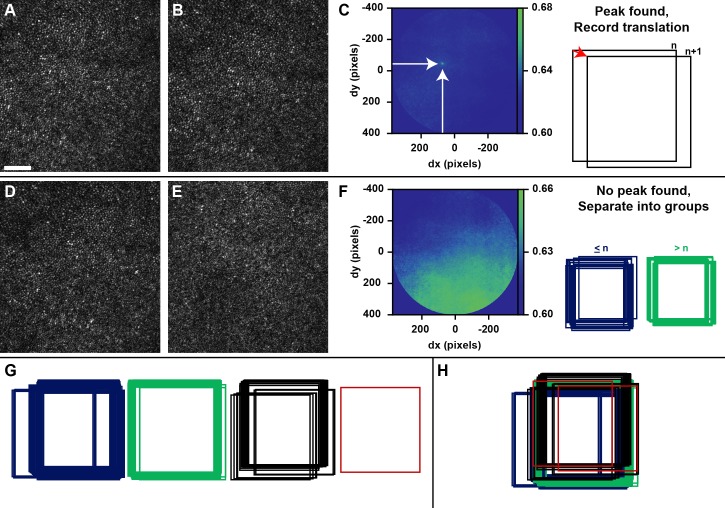
Figure 3.

Motion tracking process. (A, B) Two AOSLO frames with approximately 1 second between acquisitions. (C) The NCC matrix calculated for the frames in (A) and (B) after application of an elliptical mask (image cropped to mask boundaries). The peak of the NCC matrix is indicated by the arrows, which correspond in this case to a horizontal offset (dx) of approximately 72 pixels and a vertical offset (dy) of approximately 44 pixels. (D) An AOSLO frame from the same video as (A) and (B). (E) An AOSLO frame from a video acquired from the same subject at a different retinal location, showing an extreme example of an NCC calculated from nonoverlapping retinal areas. (F) The NCC matrix calculated for the frames in (D) and (E), processed as in (C). Because no distinct peak can be found, these frames (n and n + 1) would define the last frame in a group (D; ≤ n) and the first frame in the next group (E; > n). (G) Result of first pass of motion tracking. Relative spatial locations of the images are recorded, and frames are grouped based on successful peak finding. (H) Template and sample groups are registered to one another using a transformation vector with direction and magnitude dependent on a weighted average of NCC maxima calculated as described in the text. Scale bar, 50 μm.

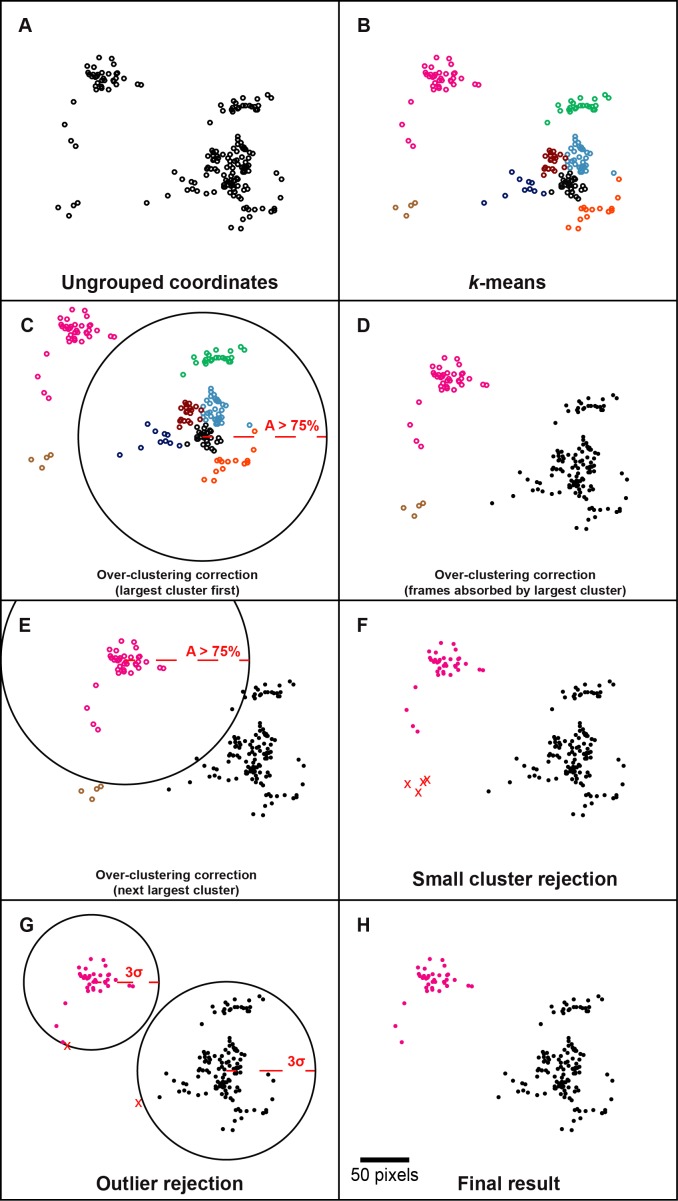
Figure 4.

Clustering process. (A) Manually simulated coordinates of frames for demonstration of the spatial clustering process. (B) Result of k-means clustering, each color represents a different cluster. For the purpose of demonstration, the number of partitions was manually set to 8, rather than using the silhouette statistic, which would have selected 3. (C) To prevent overclustering, frames may be absorbed by other clusters based on overlapping area. The large solid black circle represents the region in which a frame would overlap by more than 75% area (A > 75%) with a frame at the current cluster centroid (largest cluster absorbs first and proceeds to the smallest). (D) Filled circles represent frames whose cluster assignments are constrained after being absorbed. (E) The next largest cluster has a chance to absorb frames, but no unconstrained frames overlap with the current cluster centroid by more than 75%. The smallest cluster does not absorb any frames because at this point all other cluster assignments are constrained. (F) Clusters with fewer frames than a user-defined threshold are rejected. (G) Large solid black circles represent the boundary at which a frame is greater than 3 SDs (σ) away from the cluster centroid. Frames within the cluster but outside this boundary are rejected. (H) The final result for this set of coordinates is two spatially distinct clusters of frames from which the least-distorted frame can be determined and used as references for registration and averaging. Scale bar, 50 pixels for (A–H).

Intraframe Motion Detection

The goal of this module was to estimate distortion within frames by detecting disruptions in the characteristic frequency representation of the photoreceptor mosaic. To begin, each frame was divided into strips along the fast-scanning axis (strip size: 40 pixels) and the DFT was calculated with 512 × 512 sampling (512 is the nearest base-2 unit to the image width [∼600 pixels], chosen to optimize speed without too much aliasing). The strip size of 40 pixels was chosen because it typically encompasses two to four rows of photoreceptors (depending on field-of-view, retinal location, health, etc.) and gives an adequate sample of local photoreceptor geometry. The DFTs were cropped to the lower 25% of frequency components that, for our images, spared Yellott's ring^41,64 (an annulus representing the modal spacing of photoreceptors). Pixels less than the mean of the non-zero magnitude coefficients were set to zero to include only frequencies with a significant contribution to the image in the analysis. The maximum coefficient in each column was found, and the positions of the maxima were recorded. In a strip without distortion, the coordinates of the maxima are expected to be arranged in an annulus centered about the zero-frequency component, with a radius indicative of the modal spacing of the photoreceptors (Fig. 2B).^41,64 However, local distortion results in a shift from a circular to a more linear arrangement of the coordinates (Fig. 2C). Conducting linear regression on the coordinates of the maxima and obtaining the R² value detected this. R² values from each strip in a frame were summed, and ΣR² was used as a metric for intraframe motion. Frames with a ΣR² greater than μ + 3σ for the sequence were treated as outliers and rejected from consideration. Figure 2A shows a frame that would be rejected by this module due to its relatively high intraframe motion, compared with the frame in Figure 2D. This metric was used as the final output criterion for a minimally distorted reference frame after additional rejections by other modules (following), as it was the best independent measure of distortion employed.

Interframe Motion Tracking

Despite careful practice in image acquisition in a controlled environment, involuntary eye movements have a significant impact on the temporal and spatial relationships between consecutive frames at the level of magnification afforded by AO. Currently, humans select multiple reference frames within a video from subjectively determined spatial loci while viewing the sequence consecutively. We sought to develop this module to objectively determine the relative spatial positions of the frames, and sort them into spatial clusters (below), such that the least distorted frame from each cluster could be output automatically. To accomplish this, image-based motion tracking was conducted using full-frame NCC between consecutive frames (first pass) and groups of frames (second pass; Fig. 3). We used an implementation of NCC that was developed in-house using the Matlab function fft2.⁴⁶ The position of the maximum value in an NCC matrix signifies the linear transformation that results in maximum signal overlap. Due to edge artifacts inherent in NCC, an elliptical window was centered at the zero displacement position with radii that were two-thirds the dimensions of a frame (allowing a maximum displacement between frames of ∼400 pixels). For two frames capturing overlapping regions of the retina, there will be a distinct peak in NCC matrix with a full-width-half maximum (FWHM) related to feature size, image contrast, and distortion within and between frames.

The height of this distinct peak may not be the global maximum for the NCC matrix if there are artifacts in the image such as partial blinks, or prominent features (e.g., blood vessels, pathological hyporeflectivity, etc.) that move into view between frames due to eye motion. For this reason, we developed a custom peak-finding algorithm tailored to our distribution of image and photoreceptor sizes. First, a square mask with a side length of 21 pixels (slightly larger than the average size of the FWHM of an NCC peak) was centered on the global maximum and it was determined whether any other element in the NCC matrix exceeds 1 – (1/e) times the global maximum. If not, the global maximum was accepted as the true peak of the NCC matrix and the relative spatial positions were recorded. If there were competing local maxima, the NCC matrix was smoothed using a Gaussian kernel (size: 10 pixels, σ: 1) and the absolute values of horizontal and vertical gradients were calculated to find local maxima. The parameters of the smoothing kernel were found to be effective in eliminating low amplitude peaks without diminishing distinct peaks in our images. The horizontal and vertical gradient matrices were subjected to element-wise multiplication, and the peak of this combined matrix was detected as an outlier (μ + eσ; this time using a slightly more liberal outlier definition). If a single distinct peak could not be detected using this outlier criterion, the relative position of the sample frame was not offset from the template frame, and it was noted that no connection could be made between the template and the sample frames. Otherwise, the position of the peak in the gradient matrix was used as the center of a 21 × 21-pixel window on the NCC matrix, and the maximum and its position were calculated within that window. This process continued for each frame in the image sequence, and an approximate set of coordinates was generated from the relative offsets (Fig. 3C).

A second pass was then conducted under the assumption that connections between consecutive frames could not be made due to a large saccade. Frames were grouped based on successful peak finding, such that a new group was defined at each failure to find a peak in the NCC matrix of two consecutive frames (Fig. 3F). Groups could have length greater than or equal to 1, which allowed for the special case where the first frame in a sequence had no overlapping area with the next frame in the sequence (Fig. 3G). This is especially important for subjects with severe nystagmus, as consecutive frames rarely overlap, and it becomes necessary to attempt to align frames from across the sequence. Groups were combined by attempting to register a few key frames between a template and a sample group: the first and last frames in each group, as well as the frame nearest the template group centroid (referred to as template central). The comparisons conducted were: template first to sample first, template last to sample last, and template central to sample first. It was designed this way to minimize the number of NCC calculations while conducting a diverse search to find an overlapping area. This was conducted in order of decreasing group size and included all nonredundant group comparisons. Each time a peak was successfully detected, its position and magnitude was recorded. A transformation vector was then constructed whose direction and magnitude was determined by a weighted average of the square of the NCC peak heights detected, and the coordinates of all frames in the group were transformed by this vector (Fig. 3H). Using a weighted average vector helps ensure that the alignment of groups is biased toward high signal overlap and robust to false peak detection errors. If no connections can be made between a group and any other, it is considered an isolated group without any spatial connection to the remaining frames, and is processed separately for the remainder of the algorithm. During motion tracking, the average NCC maximum of each successful connection (note that most frames are compared twice) was recorded and used as an inference of intraframe distortion. This was used as an additional criterion for outlier rejection (NCC ≤ μ − 3σ).

Clustering

All frames whose relative positions could be determined by NCC were then sorted into spatial clusters (Fig. 4). The number of clusters was automatically determined using the silhouette statistic⁶⁵ and the cluster assignments were determined using the k-means++ algorithm (Fig. 4B).⁶⁶ The maximum number of clusters allowed in this first step was the number of remaining candidate frames divided by a threshold for the minimum number of frames per cluster set by the user. k-means was conducted with five replicates to balance speed and accuracy. Recall that groups of frames defined during interframe motion tracking could have lengths less than this threshold and would be processed separately if they could not be absorbed into another group; these groups would be rejected at this stage. During k-means partitioning, each coordinate is treated as a discrete point, rather than a range of coordinates with overlapping area, which may result in over-clustering. To account for this, a frame was absorbed into another cluster if its area had at least 75% overlap with the centroid of that cluster (Figs. 4C–E). The threshold of 75% overlap was arbitrarily chosen as a balance between improving SNR and increasing retinal coverage with multiple processed images. This progressed in order of decreasing cluster size (i.e., the number of members in a cluster). After a frame was absorbed, it could not be absorbed by any other cluster (Fig. 4E). Clusters containing fewer than the user-defined threshold for the minimum number of frames per cluster were rejected as being insufficient to boost SNR (Fig. 4F). The distance between each frame and its cluster centroid was recorded and frames that were considered outliers (μ + 3σ) were rejected. This allowed for dynamic correction of underclustering, but may benefit in the future by an absolute rejection threshold related to the aforementioned absorption threshold.

Distortion Analysis

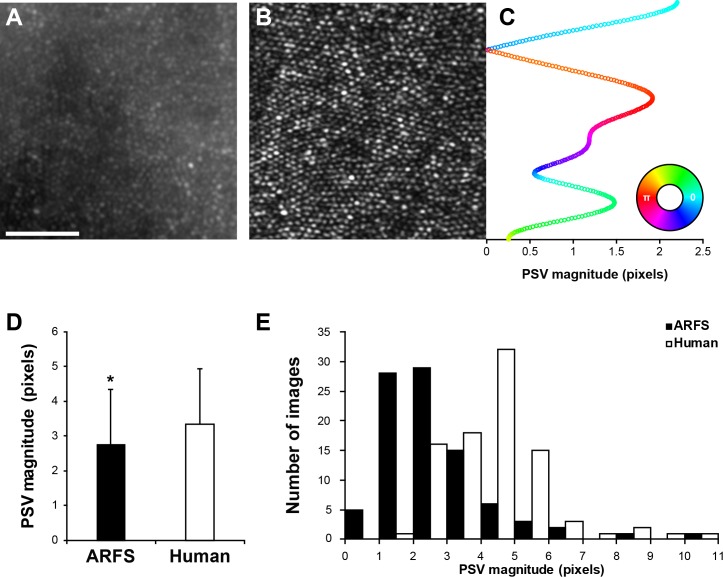
To assess the ability of ARFS to select minimally distorted reference frames, residual distortion in registered AOSLO image sequences was compared between ARFS- and manually-derived reference frames. All manually derived reference frames were identified by one expert observer (RFC). For nine healthy subjects (age: 24.6 ± 3.5 years; μ ± σ; 7 males, 2 females), 10 reference frames were selected from one video at 1° temporal from the foveola (1T; Supplementary Table S2). A 1.8° × 0.8° field-of-view (FOV) AO-flood image sequence was obtained at the same locations, and processed as previously described (Fig. 5A).⁵⁰ Briefly, AO-flood images underwent flat-field correction for uneven illumination, RFC manually selected a reference frame with minimal motion blur, and the 80 frames with the highest cross-correlation were registered to the reference frame and the stack was averaged. Averaged AOSLO images (Fig. 5B) were manually aligned to the undistorted AO-flood image in Photoshop CS6, and cropped to a common 0.55° area. The AO-flood and AOSLO images were subjected to local histogram equalization, then registered using a rigid transform in ImageJ software (National Institutes of Health, Bethesda, MD).⁶⁷ Strip-registration⁴⁶ was then conducted using the AO-flood image as the reference frame, maintaining all registration parameters set by the human observer. Distortion in the AOSLO images was calculated as the mean registration transform magnitude (henceforth, referred to as pixel shift vector, or “PSV” magnitude) for every row in the AOSLO image. A representative example for ARFS is shown in Figure 5C. The distributions of mean PSV magnitudes for each ARFS- and human-derived reference frame were compared by Mann-Whitney U test due to violation of the normality assumption requisite of parametric tests. Descriptive statistics were also calculated to determine which distribution is shifted more toward the ideal PSV magnitude (0 pixels).

Figure 5.

Distortion analysis. (A) Registered and averaged AO-flood image used as an “undistorted” template for determining distortions in AOSLO images. (B) Registered and averaged AOSLO image using either ARFS- or human-derived reference frames. (C) A representative set of pixel shift vectors (PSV) resulting from strip-registration of an AOSLO image to an AO-flood image. The magnitude of each vector is represented by its position on the x-axis and the angle is represented by the color according to the inset color-map. For example, the upper-most rows of the AOSLO image required an approximately 2.25-pixel rightward shift (cyan), the point just below this strip had nearly perfect registration with the AO-flood image (∼0 pixels), and the strip below that point required an approximately 2-pixel leftward shift (red). (D) Average PSV magnitudes using either ARFS- or human-derived reference frames for registration and averaging of AOSLO images. ARFS-derived images resulted in PSV magnitudes of 2.75 ± 1.60 pixels and human-derived images resulted in PSV magnitudes of 3.33 ± 1.61 pixels (P = 0.0016; Mann-Whitney U test; n = 90). (E) Distribution of PSV magnitudes for each approach. Scale bar, 50 μm.

Motion Tracking Validation

To validate the motion-tracking module, a motion trace was obtained from the same image sequences as in the distortion analysis (Supplementary Table S2), and each group of frames with known spatial locations were registered together and cropped to a common area. Using the first frame as a reference, the frames were reordered to minimize mean squared error (MSE) between images calculated using the Matlab function immse. The cumulative MSE for the stack of images was calculated under the assumption that registration errors would result in significant increases in MSE between frames. This was compared against the cumulative MSE for unregistered and strip-registered sequences.

Comparison of Human Frame Selection and ARFS Metrics

The agreement between human and ARFS reference frame selection was assessed. Datasets were obtained from 5 to 10 subjects each from 4 pathological categories (normal, n = 9 datasets processed by 7 observers; subject age: 25.2 ± 3.2 years; 7 males, 2 females), achromatopsia (ACHM; n = 10 datasets processed by 9 observers; subject age: 24.4 ± 12.1 years; 5 males, 5 females), albinism (n = 5 datasets processed by 1 observer; subject age: 16.2 ± 12.9 years; 5 females), and retinitis pigmentosa (RP; n = 10 datasets processed by 6 observers; subject age: 39.5 ± 13.8 years; 6 males; 4 females; Supplementary Table S3). The discrepancy in the number of datasets is the result of an initial examination of an arbitrary division of datasets between beginner and expert reference frame selectors. No significant difference was found between the groups so the data were pooled. All albinism datasets were processed by a single “expert,” so only five were included. For this analysis, the minimum frame per cluster threshold in ARFS was held at five. The proportion of frames selected by humans that were not rejected by ARFS was calculated, and for those that were rejected, the module responsible for the rejection was recorded. Because intraframe motion is our final determinant for ranking, we determined the intraframe motion rank of each frame selected by humans and determined the distribution of ranks for each pathological category.

Results

Distortion Analysis

ARFS-derived reference frames resulted in a significant decrease in residual distortion relative to manually derived reference frames. ARFS- and human (RFC)-derived reference frames resulted in PSV magnitudes of 2.75 ± 1.60 pixels and 3.33 ± 1.61 pixels (P = 0.0016; Mann-Whitney U test; n = 90), respectively (Fig. 5D). The medians for the PSV distributions were 2.42 and 3.29 pixels for ARFS and RFC, respectively. The skewness for ARFS was +2.12 and +1.33 for RFC, indicating ARFS was more right-skewed (Fig. 5E).

Motion Tracking Validation

ARFS-registered sequences reduced cumulative MSE compared with unregistered sequences, but not as well as strip-registered sequences. The average slope of increasing MSE of unregistered, ARFS-registered, and strip-registered sequences are 0.063, 0.044, and 0.022, respectively (Fig. 6). From a visual inspection of all registered videos, it was found that the ARFS motion tracking process led to a registration error in a few videos of approximately 10 pixels, but the primary source of the increased MSE was local distortion between frames, which is not corrected for by full-frame NCC (Supplementary Video S1).

Figure 6.

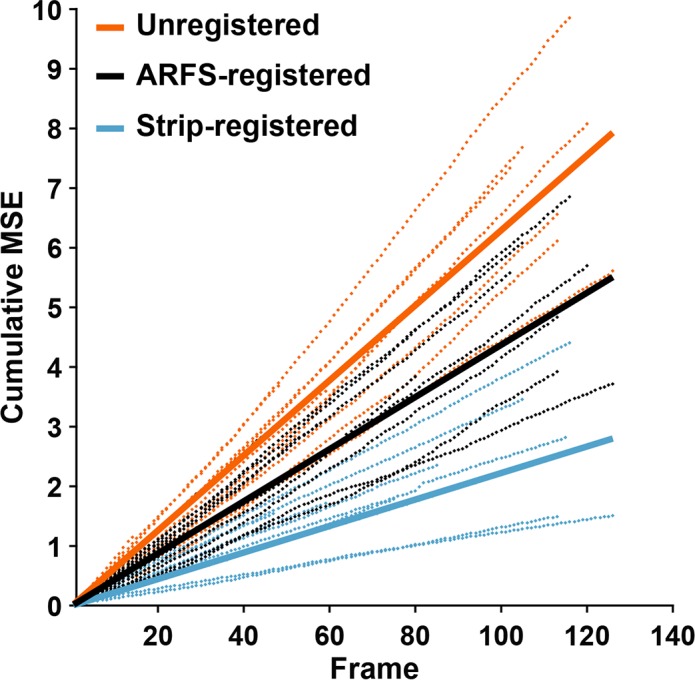
Motion tracking validation. (A) Raw AOSLO frame representing an unregistered image sequence. (B) Frame outlines with relative spatial locations representing full-frame registration using the motion-tracking module described here. (C) An AOSLO frame that has been subjected to strip registration.⁴⁶ Note the nonlinear warping likely to result in decreased MSE between frames. (D) Each dotted line represents a separate group of frames analyzed. The grouping was determined by successful peak finding by the motion-tracking module, and the groups were maintained for each registration method. Solid lines represent a linear regression of all the dotted lines for a certain registration method; the slope (m) of which gives an estimate of the average performance of each registration method. Orange: unregistered frames, m = 0.063. Black: registered according to the relative positions calculated by the motion tracking module, m = 0.044. Cyan: Strip registered, m = 0.022.

Comparison of Human Frame Selection and ARFS Metrics

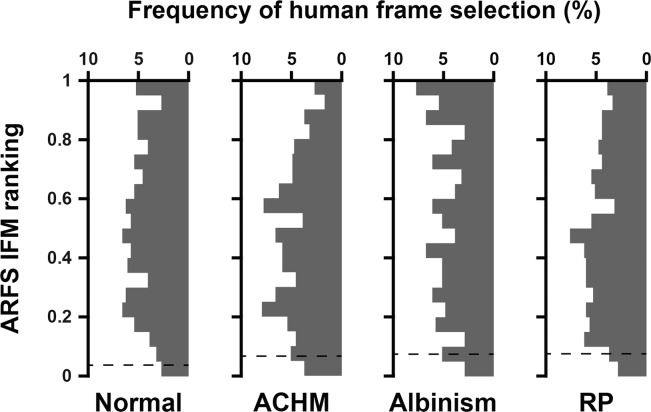
Humans were more likely to select a reference frame rejected by ARFS for videos acquired from subjects with pathology than for subjects with healthy retinas, varying widely from 5.16% to 39.22% (Table 1). The most common ARFS rejection method, on average, for all human-derived reference frames was cluster size, ranging from 0.32% to 21.39% of frames, while the least common was mean pixel intensity, ranging from 0% to 0.36% of frames. It was relatively uncommon that a human would select a frame that was rejected based on intraframe motion, with a range of 1.94% to 5.35%. More commonly, humans would select frames that were rejected based on NCC, ranging from 2.26% to 12.30%. Figure 7 shows the distribution of intraframe motion rankings of human-derived reference frames (1 is best, 0 is worst). 5.24, 2.71, 7.73, and 3.89% (normal, ACHM, albinism, and RP, respectively) of human-derived reference frames ranked in the 95^th to 100^th percentile for intraframe motion. Put another way, on average, humans selected a minimally distorted reference frame 4.89% of the time.

Table 1.

Comparison of Human Frame Selection and ARFS Metrics

Figure 7.

Intraframe motion ranks of human derived reference frames. Histograms of intraframe motion ranking (1 is best, 0 is worst) of human-derived reference frames for videosobtained from subjects with normal retinas, ACHM, albinism, or RP. Frames below the horizontal dashed lines were rejected by the intraframe motion module (1.94%, 5.35%, 5.33%, and 4.66% for normal, ACHM, albinism, and RP, respectively).

Discussion

The results from the distortion analysis show that ARFS can automatically select minimally distorted reference frames from AOSLO image sequences. Automatically determining minimally distorted frames is an important step in validating the technique of AOSLO, and increases the accuracy of measures of photoreceptor geometry.⁵⁰ It is important to note that even the least-distorted image in a sequence may be unacceptably distorted, as is often the case with images obtained from patients with nystagmus. For example, if the frame with the lowest ΣR² value for the sequence had an average R² of 0.5, it is likely that this frame would be visibly distorted, but because ARFS does not employ absolute thresholds, it would still be output as the “minimally distorted frame” from that image sequence. Thus, the burden still lies on the user to verify that the reference frames selected are likely accurate representations of the subject's retina. This problem could eventually be corrected if the measurements from ARFS were aggregated for a large number of subjects and used to create absolute thresholds for acceptable intraframe motion and NCC values. Further, rather than selecting the least-distorted frame, some of the measurements made by ARFS could be combined to construct an artificial frame from the least-distorted regions of multiple frames to best approximate an undistorted image.^47,48,50

When examining Table 1, it is important to note that rejection criteria are intentionally strict, and perceptually acceptable frames may be rejected. Further, all rejections are based on statistics calculated for sets of observations that are commonly not normally distributed, which warrants further investigation into more complex statistical criteria for rejection. This approach is useful as it is adaptive and accounts for a wide range of factors that influence the images, such as tear-film and fixation instability, lens opacity, and detector gain. Approximately 95% of human-selected frames from healthy subjects were not rejected by ARFS, which suggests that when a frame is determined to be an outlier, it is probably obvious enough for a human to recognize. The remaining 5% almost certainly harbored subtle distortions that were missed by humans. It is apparent that ARFS and humans agree less when examining image sequences obtained from subjects with pathologies. With nystagmus, it becomes difficult to estimate eye motion for an image sequence unless there are prominent and unique features present. Because ARFS compares groups of frames from across the image sequence, where humans are usually confined to viewing them in order, it is better equipped to assign frames to spatial groups and build clusters of frames. A human may see a minimally distorted frame out of its spatial context, but it would fail to register due to insignificant overlap. This is a possible explanation for the relatively high proportion of human-selected frames rejected by the cluster-size method. One alarming finding is the frequency at which humans select frames that are rejected based on intraframe motion or NCC, which means that any metrics extracted from those processed images are likely to be confounded by significant local distortions. This is especially concerning in cases of disease, where the presence of these distortions may confound our metrics, and thus our understanding, of the organization of the retina.⁵⁰

The distributions in Figure 7 are not skewed toward highly ranked frames as one might expect, indicating that humans do not tend to select frames objectively determined to be minimally distorted. Severe eye motion can significantly reduce the population of perceptually acceptable frames, increasing the likelihood for humans to select a minimally distorted frame; this may explain the increase in selection of the top 5% of frames in the albinism datasets relative to normal datasets. The roughly even distributions highlight the difficulty in selecting the least distorted frame in a sequence. While there may be a large population of seemingly acceptable frames, the least distorted frame will yield the most accurate measurements of the photoreceptor mosaic.⁵⁰

With 32-GB random access memory and a 3.30-GHz central processing unit, ARFS processing time for a video may range from approximately 2 to 8 minutes per video, depending on the amount of eye motion and subsequent number of frame groups. The rate-limiting step is calculating NCC matrices, which is more computationally complex than other registration methods, but more robust to variations in illumination and image features.⁴⁶ While expert observers may select frames at a rate of approximately 2 frames/minute, setting the parameters to run ARFS on a dataset (frequently comprising hundreds of image sequences) requires approximately 2 to 5 minutes, which drastically reduces the total human interaction time.

It is important to note that many parameters used in this algorithm were determined empirically based on our distribution of image and feature sizes (∼600 × 600 pixels and 5–10 pixels, respectively), and may need to be adjusted for use with other systems and image sets (Supplementary Table S1). This is especially important for the intraframe motion calculation, which assumes a range of photoreceptor spacing before cropping the DFT. With significantly increased or decreased magnification, too little of the relevant frequency components or too many irrelevant frequency components, respectively, would be included, and thus decrease the sensitivity and specificity of the analysis. A potential solution to this example would be estimating modal spacing with automated detection of Yellott's ring^41,64 to inform the size of the cropping window. Further investigation into dynamically optimizing the parameters employed by ARFS is warranted.

A major limitation of this algorithm is its image feature-specific nature. Currently, ARFS only functions properly on confocal images of the cone photoreceptors. The intraframe motion module was designed to detect disruptions to a mosaic of regularly spaced circular objects, and as such, would have an adverse effect when applied to images of the nerve fiber layer or capillaries. Adaptations of other methods may bridge this gap.⁵² Further, ARFS performance has not been rigorously tested in image sequences where there is significant disruption to the cone mosaic such that ARFS may mistake aberrantly shaped or organized cones as being compressed or stretched. Subjectively, sampling a large strip of the retina typically makes the intraframe motion module robust to such disruptions, and tuning this parameter may resolve this issue. In the conceivable event that a motion artifact expands a patch of cones that are pathologically compressed, the intraframe motion module may be biased to select this frame; however, it is also possible that this frame would be rejected due to a weak NCC peak height caused by intraframe motion.

Our lab also collects multiply scattered nonconfocal AOSLO images referred to as split-detector²³ and dark-field,²⁴ but ARFS does not currently function properly on these modalities. The broader intensity profile in the features of these images results in overmasking of the DFT's during the intraframe motion module, and the peaks of the NCC matrices are wider than for confocal, rendering the peak-finding algorithm ineffective during the motion tracking module. For subjects with pathologies affecting the wave guiding of cone outer segments, such as ACHM, cone inner segments are still visible in split-detector images.¹⁹ Using the registration transforms for split-detector images and applying them to simultaneously acquired confocal images has been useful in identifying any residual signal in the confocal channel that would otherwise be too weak to use for registration. Thus, there is significant motivation to adapt ARFS to other modalities and image features using more generalizable methods.