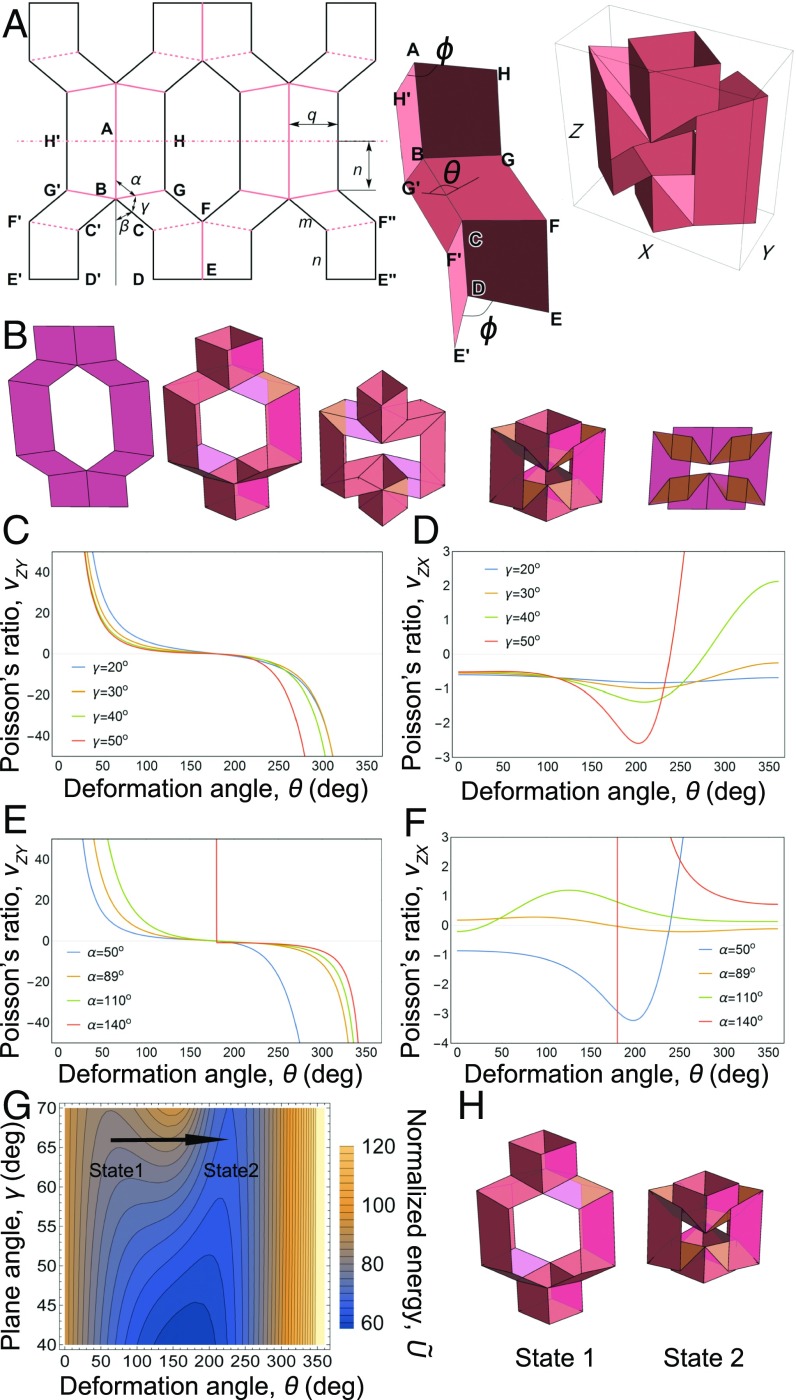
Fig. 1.

Geometry-driven metamaterial properties of a kirigami lantern-like module. (A) The design pattern of one module (Left) involves cutting a thin sheet along the thick black lines, then folding along the mountain (dashed) and valley (solid) creases. Edges $BCD$ and $BC\prime D\prime$ are bonded to create crease-like hinges in each of the four symmetric quadrants. Similarly, $F\prime E\prime$ is bonded to $F^{″}{E}^{″}$, along with the symmetric edges in the module’s upper half. The plane angle parameters $\alpha$ and $\gamma$ and lengths $m$, $n$, $q$ determine the 3D structure shown in the $1/4$ (Middle) and full (Right) unit module. The dihedral angle $\theta$ is chosen to quantify the module’s configuration. Parameters $\varphi$ and $\beta$ are useful for the mathematical description of the geometry (Materials and Methods). (B) The module takes various forms determined by the configuration angle $\theta =0°,90°,180°,270°,$ and $360°$. Poisson ratios (C) ${\nu }_{ZY}$ and (D) ${\nu }_{ZX}$ as functions of folding configuration for $\alpha =60°$ and $\gamma =20°,30°,40°,$ and $50°$. Poisson ratios (E) ${\nu }_{ZY}$ and (F) ${\nu }_{ZX}$ as functions of folding configuration for $\gamma =40°$ and $\alpha =50°,89°,110°$, and $140°$. Calculations in C–F use $m/q=n/q=1.5$. (G) The normalized elastic energy $\stackrel{\sim }{U}$ as a function of $\gamma$ and $\theta$ for parameter values $\alpha =100°,m/q=n/q=1$, $k_2/k_1=1.5$, and ${\theta }_0=10°$. Arrow indicates the module undergoes a bistable transition between two energetic minima during folding. (H) The module’s configuration for the two mechanically stable states in G. Reading left to right in B and H corresponds to compression along $\widehat{z}$, whereas right to left corresponds to tension along $\widehat{z}$.