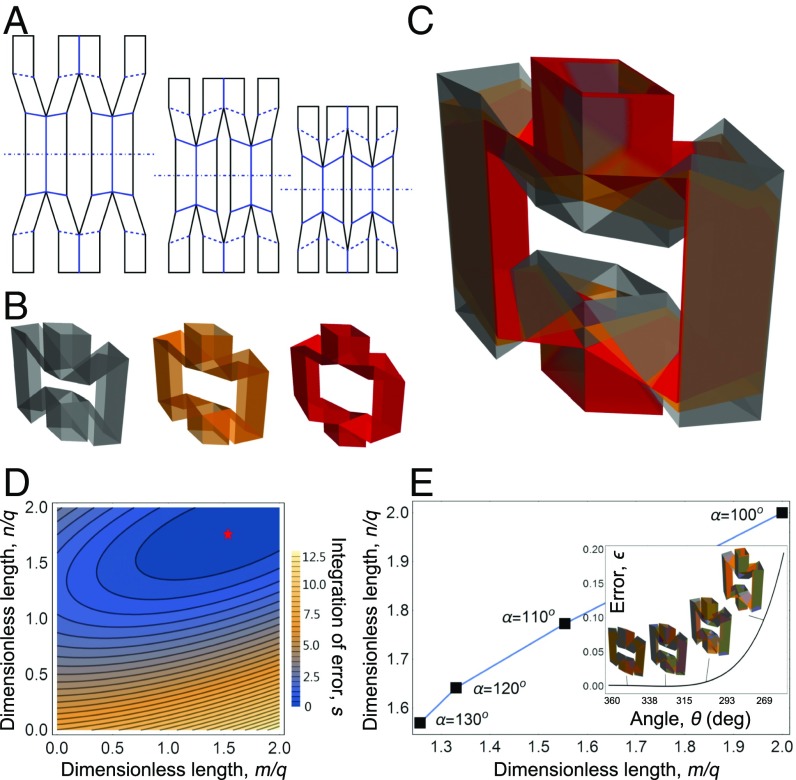
Fig. 2.

Geometric compatibility of modular kirigami voxels. (A) Design patterns and (B) structure for three geometrically compatible voxels where the first structure (gray: $\alpha =100°,\gamma =62.4°$ and $m/q=n/q=2$) is the target, and the second (orange: $\alpha =110°,\gamma =57.7°,m/q=1.55$, and $n/q=1.77$) and third (red: $\alpha =120°,\gamma =51.2°,m/q=1.33$, and $n/q=1.64$) are determined by parameter optimization over a prescribed folding domain. (C) Overlapping the three voxels shows how different design patterns can simultaneously satisfy the $N_c=4$ conditions for geometric compatibility in $X$, $Y$, $Z$, and $\mathrm{\angle }EDE\prime$ (e.g., $X_{\text{gray}}=X_{\text{orange}}=X_{\text{red}}$ and $Y_{\text{gray}}=Y_{\text{orange}}=Y_{\text{red}}$, etc.). This mutual consistency allows geometrically compatible voxels to be interchangeable within a large-scale structure assembled from a mechanically heterogeneous collection of modules. (D) Identifying geometric compatibility requires minimizing the integrated error $s$ over the design parameters. This projection of parameter space shows the local minimum of $s$ (red star) as a function of dimensionless lengths $n/q$ and $m/q$. (E) Varying folding angle $\alpha$ changes the optimal values of $n/q$ and $m/q$ that minimize error between the target structure and the structure being optimized for geometric compatibility. (Inset) The error function from which we calculate and minimize the integrated error $s$.