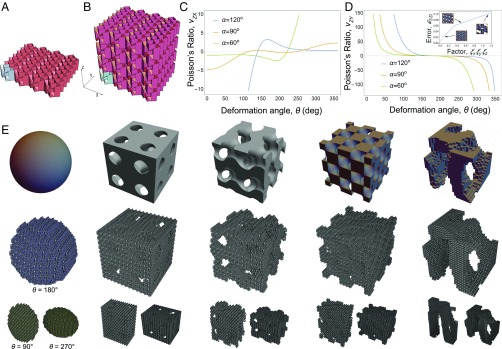
Fig. 4.

Assembly of kirigami modules into voxelized 3D mechanical metamaterials. (A) Tessellating voxels in the $\widehat{x}\widehat{y}$-plane leads to metamaterials that are (B) stackable along the $\widehat{z}$-axis. These structures have mechanical properties independent of their ability to tessellate 3D space. Plots of the Poisson ratios (C) ${\nu }_{ZX}$ and (D) ${\nu }_{ZY}$ as a function of deformation angle $\theta$ show a wide range of allowable behaviors for the same $4\times 7\times 4$ cuboid bulk structure in B, but with variable parameters for $\alpha$ and $\gamma$. For the plots shown here, we chose $\gamma =\text{arcsin}[(9/10)\sin (\alpha )]$ to obtain a wide variety of behavior in ${\nu }_{ZX}$. D, Inset shows the error ${ϵ}_{3D}$ between target 3D structure and voxelized 3D structure as a function of the product of scaling factors ${\xi }_x,{\xi }_y$, and ${\xi }_z$ (Materials and Methods). Larger values of $\xi$ lead to larger voxels with a coarser approximation of the target structure, whereas lower values of $\xi$ have smaller voxels and a more fine approximation. (E) The top row shows five target 3D structures representing a sphere, three triply-periodic minimal surfaces, and a digitized micro-CT scan of a mouse femur bone. The second and third rows are renderings of the different voxelized 3D metamaterials with folding configurations given by $\theta =90°,180°$, and $270°.$ Increasing $\theta$ corresponds to compression along $\widehat{z}$, whereas decreasing $\theta$ corresponds to tension along $\widehat{z}$. Although all structures have identical compressive properties ($\alpha =60°,\gamma =51°$, and $m/q=n/q=1$), the scaling factor triplets $⟨{\xi }_x,{\xi }_y,{\xi }_z⟩$ are $⟨0.37,0.21,0.26⟩$ for the sphere and triply-periodic minimal surfaces, whereas the micro-CT scan has $⟨{\xi }_x,{\xi }_y,{\xi }_z⟩=⟨8,9,5⟩\times {10}^{-3}$. These large-scale metamaterials highlight the complex topology that can be achieved independent from the prescribed mechanical properties using the $N_p-N_c>0$ design strategy.