Gating Charge Calculations by Computational Electrophysiology Simulations

Abstract

Electrical cell signaling requires adjustment of ion channel, receptor, or transporter function in response to changes in membrane potential. For the majority of such membrane proteins, the molecular details of voltage sensing remain insufficiently understood. Here, we present a molecular dynamics simulation-based method to determine the underlying charge movement across the membrane—the gating charge—by measuring electrical capacitor properties of membrane-embedded proteins. We illustrate the approach by calculating the charge transfer upon membrane insertion of the HIV gp41 fusion peptide, and validate the method on two prototypical voltage-dependent proteins, the Kv1.2 K⁺ channel and the voltage sensor of the Ciona intestinalis voltage-sensitive phosphatase, against experimental data. We then use the gating charge analysis to study how the T1 domain modifies voltage sensing in Kv1.2 channels and to investigate the voltage dependence of the initial binding of two Na⁺ ions in Na⁺-coupled glutamate transporters. Our simulation approach quantifies various mechanisms of voltage sensing, enables direct comparison with experiments, and supports mechanistic interpretation of voltage sensitivity by fractional amino acid contributions.

Introduction

Many ion channels, transporters, neurotransmitter receptors, and enzymes change conformation in response to changes in the transmembrane voltage (V_m); the consequent voltage-dependent changes in function are critical for a large number of processes in excitable and nonexcitable cells. The voltage dependence of membrane protein function is caused by global or localized conformational changes, ion or ligand binding, protonation, or changes in water accessibility that reshape the electric field (1). It can be quantified as transmembrane charge transfer, often denoted as the gating charge (Q_g), i.e., the effective number of charges that need to be moved across the whole electric field to provide the electric energy necessary for these changes. In recent years, experimental methods have been developed to quantify Q_g and study the molecular determinants of voltage dependence, resulting in great progress in understanding the principles of voltage sensing (2, 3).

Computer simulations based on structures of various voltage-dependent membrane proteins in multiple conformations enable structural information to be linked to function. Poisson-Boltzmann calculations provide satisfying estimates of Q_g for classical voltage-gated cation channels (2, 4, 5, 6) or transporters (7, 8). In particular, the recently developed APBSmem program greatly facilitates Poisson-Boltzmann simulations of membrane proteins (9, 10). Unfortunately, its representation of the ionic solution and membrane as a dielectric continuum, and the simplified geometry of the dielectric boundaries limit the suitability of the PB model, for instance when changes in water accessibility refocus the electric field within narrow protein crevices (11, 12). Recent coarse-grained models have been useful in simulating the dynamics of the gating charge transfer, but still carry the inherent risks of implicit solvent representation and a simplified protein description (13). Molecular dynamics (MD) simulations may consider all possible mechanisms of voltage gating (14, 15, 16, 17, 18), but usually come at a high computational cost. To gain insights into the underlying mechanisms and to permit validation by mutagenesis experiments, it is important to quantify the contributions of individual residues to the overall voltage sensitivity. Thus far, two MD approaches have been used to this end. One approach analyzes changes in electrical distance—that is, the fraction of the electric field across the membrane—of certain residues by evaluating the dependency of the local electrostatic potential on V_m (14, 17, 18). This approach has provided important mechanistic insights, but is limited by the need to calculate the electrostatic potential in three dimensions, and the convergence of the local potential and the statistical accuracy of the calculated Q_g contributions have not been investigated in these studies. In other studies, perturbative free energy calculations have been used to determine the Q_g contributions via the charging free energy of certain amino acids (16, 18). These simulations are computationally expensive, and thus difficult to be routinely applied to a large number of residues.

To overcome these limitations, we developed a user-friendly and efficient method for gating charge calculations using computational electrophysiology (CompEL) simulations (19, 20). Our approach enables accurate estimates of the voltage sensitivity and provides mechanistic insight via directly determining the fractional amino acid contributions to Q_g. It is based on the simulation of the membrane/protein capacitor charging process, as pioneered by Treptow et al. (17), and permits direct determination of Q_g and the change in capacitance associated with any conformational change, taking all possible components of voltage sensitivity explicitly into account.

Materials and Methods

MD simulations

MD simulations were carried out using GROMACS 5 (21). The AMBER99SB-ILDN force field (22) was used for the voltage-sensing domain of the Ciona intestinalis voltage-sensitive phosphatase (Ci-VSD), Kv1.2, and Glt_Ph, and the GROMOS 43a1 force field (23) was used for the gp41 peptide. All amino acids were modeled in their default ionization state; in Kv1.2 all histidine residues were assigned a protonated state with a charge of +1 e to reflect the most probable state at neutral pH according to pKa calculations on this channel (16). In simulations with the AMBER force field, ion parameters were taken from Joung and Cheatham (24). All simulation boxes contained equilibrated palmitoyloleoyl phosphatidylcholine bilayers (25), except for gp41, where dimyristoyl phosphatidylcholine (26) was used. Ions were added to obtain bulk concentrations in the aqueous solutions of 100 mM KCl for all simulations, except for gp41, which used 70 mM NaCl. Water was modeled using the SPC/E water model (27) in all simulations, except for gp41, where SPC (28) was used. Using virtual sites for hydrogen atoms enabled simulations to be performed with 4 fs time steps.

Membrane proteins were embedded into each membrane using g_membed (29), informed by the Orientations of Proteins in Membranes database (30), while ensuring that S1 and S2 helices of the activated and resting states were superimposed (31). Before production runs, single-bilayer systems were equilibrated in the absence of transmembrane voltage during 100–500 ns simulation with position restraints on the protein heavy atoms, followed by ∼20 ns with backbone-only position restraints.

Initial structures used for the simulations of Ci-VSD in the down- and up-states were taken from the Protein Data Bank (PDB): 4G80 and 4G7V (15), respectively, using the residue range 106–236. The up-state structure of Ci-VSD (PDB: 4G7V) carried the mutation R217E, which was reverted to wild-type using the software MODELLER 9.10 (32). Kv1.2 structures were taken from Pathak et al. (5), using the residue range 32–421. The gp41 fusion peptide simulation system is derived from a single-layered MD setup in Gapsys et al. (33), and the peptide structure originates from Charloteaux et al. (34). The Glt_Ph crystal structures used in this study are symmetric, outward-facing trimers either in an apo (PDB: 4OYE) or in a sodium-only bound state (PDB: 4OYF), using the residue range 6–416 (35). The sodium-only structure shows the Na1 ion. So far, the second Na⁺ ion, termed Na3, has not been resolved in any Glt_Ph crystal structure. However, it has been predicted by electrophysiology (36) and MD simulations (37), and was recently resolved in a novel aspartate-bound structure of another prokaryotic transporter homolog, Glt_Tk (38). However, because no sodium-only bound Glt_Tk structure is available, we decided to use Glt_Ph in this study. Glt_Ph and Glt_Tk share highly similar sequence and structure, and the residues forming the Na3 site are identical. We manually inserted the Na3 ion in the sodium-only Glt_Ph structure according to the Glt_Tk position (38), and found this configuration to be stable in free MD simulations on a timescale of 1 μs.

Computational electrophysiology setup

For the gating charge calculations, we used an antiparallel configuration of two lipid bilayers, both containing the same membrane protein in the same state, adopting the CompEL method (19, 20). The simulation system is created by duplicating a fully equilibrated single-bilayer/protein configuration along the membrane normal, with the copied bilayer being inverted. The size of the simulation box was chosen such that the minimum distance between the two membrane proteins, within the box and across periodic boundaries, was always >40 Å. Thus, interactions between the proteins are negligible, stable density profiles in the bulk region are established, and V_m is well defined. Electroporation through the lipid membrane was not observed in any simulations in this study.

Calculation of the gating charge

After setting up the CompEL systems, the activated/up-state and resting/down-state proteins were further equilibrated—without position restraints—in the presence of +100 or −100 mV, respectively, for ∼500 ns. Position restraints on the protein heavy atoms were then turned on again, using spring constants of 1000 kJ mol⁻¹ nm⁻². Finally, the charge titration simulations, i.e., multiple CompEL runs with different ionic charge imbalances, were conducted for ∼80–100 ns for each condition. The use of position restraints is not always required, as V_m(q_exc,sol) converges within less than a nanosecond (Fig. S1 b in the Supporting Material), i.e., faster than most voltage-dependent conformational changes of the protein might take. Nevertheless, the position restraints ensure that the reported gating charges can be assigned to specific conformational states of the protein. Finally, the analyses were performed as described in the main text using Eqs. 3 and 4.

Integration of the charge densities and calculation of V_m by Eq. 2 were performed individually on each frame of the MD trajectory. Consequently, the V_m(q_exc,sol) relationships were fitted globally by Eq. 3 to determine q_exc,p,λ and C_mp,λ; bootstrap sampling was used to determine standard deviations of the fit parameters.

Numerical errors during the double integration of the charge densities led to small deviations in the electrostatic potential across the periodic boundary. To circumvent this problem––assuming a neutral simulation system—the floating-point sum of all charges divided by the number of all nonzero charges was subtracted from the charges of all charged atoms in the system. This procedure effectively ensures that the electrostatic potential is the same at the upper and lower edge of the simulation box, and is, for example, available in the gmx potential module of GROMACS (21, 39). If certain charged atoms are excluded from the analysis, e.g., to investigate the influence of an amino acid on V_m and Q_g, then this procedure will implicitly offset all other nonzero charges by a very small value, thereby keeping the remaining system neutral.

Results

Calculation of gating charges by charge titration simulations using CompEL

The CompEL protocol (19, 20), introduced into GROMACS (21), enables simulations under realistic transmembrane potentials by all-atom MD (40). Using an ion/water exchange procedure, CompEL generates electrochemical potential gradients by maintaining slight differences in ion numbers between two aqueous compartments in a double-bilayer simulation system (Fig. 1 a). CompEL induces excess charges q_exc,sol in the aqueous compartments (positive sign, intracellular; negative, extracellular), which result in a well-defined V_m that can be determined by solving Poisson’s equation (41)

$$\frac{d^2\psi }{d{z}^2}=-\frac{1}{{\mathit{ϵ}}_0}\times \sum _i{q}_i\times {\rho }_i\left(z\right),$$ (1)

$$\psi \left(z\right)-\psi \left(0\right)=-\frac{1}{{\mathit{ϵ}}_0}\sum _i{q}_i\times \underset{0}{\overset{z}{\int }}d{z}^{\prime }\underset{0}{\overset{z^{\prime }}{\int }}{\rho }_i\left(z^{″}\right)d{z}^{″},$$ (2)

where ψ(z) is the electrostatic potential profile along the membrane normal, and q_i and ρ_i(z) are the charge and the charge density, respectively, of atom i in the MD trajectory. When the membrane proteins are centered in the simulation box, ψ(z) and the first integral of ρ_i(z), the electric field, will be set to zero at z = 0 as boundary conditions. Because the CompEL setup behaves as an ideal electrical capacitor (Fig. S1), V_m depends on q_exc,sol as

$$V_m\left(q_{\text{exc,sol}}\right)=\frac{q}{2C_{\text{mp},\lambda }}=\frac{q_{\text{exc,sol}}+2q_{\text{exc},p,\lambda }}{2C_{\text{mp},\lambda }},$$ (3)

where C_mp,λ is the capacitance of each of the two lipid bilayers including the protein in state λ. The charge distribution within membrane proteins is usually uneven along the membrane normal, and will be hereafter represented by excess charges ±q_exc,p,λ for each of the two identical proteins (positive sign, intracellular side; negative, extracellular). q_exc,p,λ describes how the protein in state λ contributes to the total capacitor charge on each side of the membrane. To obtain q_exc,p,λ from MD simulations, we constructed CompEL simulation systems for the membrane protein in both the assumed active and resting states, starting from an equilibrated single-bilayer system. The membrane was then duplicated along the z axis, with one bilayer inverted to obtain an antiparallel orientation. This results in application of identical voltages to the two membrane proteins such that the effects of the excess charges of both proteins are additive. Subsequent charge titration simulations—i.e., CompEL simulations at various ionic charge imbalances—provide the V_m(q_exc,sol) relationship that is fitted by Eq. 3 to determine q_exc,p,λ and C_mp,λ. The charge titration simulations for resting and activated states of the protein provide the gating charge via Eq. 4:

$$Q_g=q_{\text{exc},p,\text{rest}}-q_{\text{exc},p,\text{act}}.$$ (4)

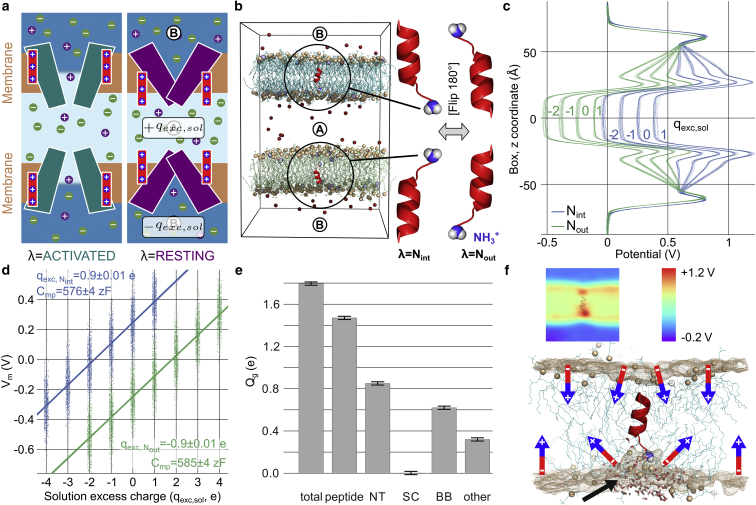
Figure 1.

Gating charges by membrane charge titration. (a) Setup of two antiparallel CompEL systems with an activated or resting ion channel. (b) gp41 fusion peptide inserted into each bilayer with charged N-termini either pointing inward (N_int) or outward (N_out), illustrating a simple electrogenic conformational change. (c) Averaged electrostatic potential profiles along the membrane normal from 100 ns simulations of the two systems in (b) with different charge imbalances (n = 10 for each condition). (d) Charge titration plot reveals a gating charge of 1.79 ± 0.02 e (dots, calculated electrostatic potential for each frame of the trajectory; solid lines, linear fits according to Eq. 3). (e) Contributions of the N-terminus (NT), side chains (SC), backbone dipole (BB), and membrane deformation (other) sum up to the total gating charge of 1.79 e. Error bars show SD, determined through bootstrap sampling (see Materials and Methods). (f) gp41 induces an asymmetric deformation of the membrane. (Top) Slice through an electrostatic potential map. (Bottom) Close-up of the peptide shows curvature of the membrane leaflet near the N-terminus (black arrow). (Brown spheres) Phosphate groups of nearby lipid molecules, and their average density, respectively. (Colored arrows) Dipole moment of the lipid molecules.

According to Eq. 2, the electrostatic potential depends on the additive effects of individual charges. Thus, the specific contribution of, for example, certain amino acids to the voltage sensitivity can be determined by excluding the charges of a group of atoms from the sum over the charge densities in Eq. 2. When a charged residue is excluded, the charges of all other atoms in the system are slightly offset to maintain neutrality of the total system and to increase the accuracy of the numerical integration (see Materials and Methods). Subsequent analysis by Eq. 3 will then provide the altered Q_g as if the residue under consideration were neutral; subtraction from the total Q_g of the protein yields the specific contribution of that residue. Thereby, the contributions of all amino acids, bound ligands, or lipid molecules can be determined without running new simulations. This implies a linear decomposition of the charge contributions and is thus an approximation. We evaluated this approach by additional MD simulations of neutralizing mutations on the S4 segment of a VSD and found that our charge-exclusion method provides a good approximation of the gating charge contributions (Fig. S2). Furthermore, we note that this approach requires the gating states to be robust against modification of individual residues. This assumption is reasonable, and is implied in every experimental approach for probing individual residue contributions to voltage sensing.

In the following, we illustrate gating charge calculations using CompEL on the membrane insertion of the gp41 fusion peptide, and then test it on two proteins, for which a large body of experimental data exist: the VSD of the Ciona intestinalis voltage-sensitive phosphatase (Ci-VSP), and the Kv1.2 K⁺ channel. Finally, we employ the approach to quantify the role of the cytoplasmic T1 domain in Kv1.2 voltage sensing and the voltage dependence of Na⁺ binding to the glutamate transporter homolog Glt_Ph.

Voltage dependence of membrane insertion of HIV gp41

The N-terminal fusion peptide of the HIV protein gp41 consists of a 12-amino-acid α-helix with a positive N-terminus and mediates HIV envelope fusion with the T-cell membrane (34). We assumed that gp41 may insert into the target membrane in two states defined by 180° rotation of the α-helix, then constructed two CompEL systems (Fig. 1 b) and performed charge titration simulations for each conformation (Fig. 1, c and d). Fitting the charge titration plots with Eq. 3 reveals a gating charge of 1.79 e associated with this flip. Voltage may thus alter gp41 membrane insertion and influence susceptibility to HIV infection. Decomposition of the gating charge reveals that contributions are made by the N-terminus and the backbone (Fig. 1 e), but also by an asymmetric curvature of the bilayer around the charged N-terminus (Fig. 1 f). This weakens the influence of the dipole contributions of nearby lipid molecules to V_m and contributes to the total Q_g by 0.32 e. By decomposing the gating charge into molecular contributions, the charge titration approach thus reveals additional mechanisms of voltage sensing.

Gating charges conferred by voltage-sensing domains

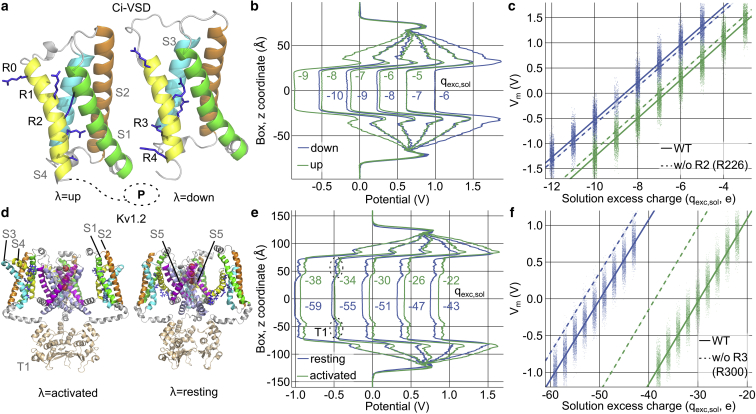
We next determined gating charges for the VSD of the Ciona intestinalis Ci-VSP and the Kv1.2 K⁺ channel. In Ci-VSP, the VSD transduces depolarization to activation of an enzyme that dephosphorylates cellular signaling molecules such as phosphoinositides (42). Membrane depolarization induces opening of the K⁺-selective pore of Kv1.2, and the resulting K⁺ efflux contributes to repolarization during action potentials in various cell types. Ci-VSD and Kv1.2 have been extensively studied to understand voltage sensing by voltage-gated Na⁺, K⁺, and Ca²⁺ channels in excitable tissues. For both proteins, high-resolution structures for an activated and a resting state (Fig. 2, a and d) have been determined by x-ray crystallography (15) or computational structure prediction and refinement based on x-ray and functional data (5, 31, 43). We decided to use the Kv1.2 models from Pathak et al. (5); these models also include the intracellular T1 domain, and have been thoroughly tested against experimental data and shown to be consistent with other structure predictions (31, 43). Both Ci-VSP and Kv1.2 contain a VSD made up of four helices (S1–S4), with S4 containing several positive side chains, but differ in the extent of voltage-dependent rearrangements (15).

Figure 2.

Gating charge calculations for Ci-VSD and the Kv1.2 K⁺ channel. (a and d) Structures of (a) Ci-VSD in the up- and down-states (15) (location of the phosphatase domain indicated by dotted lines) and (d) activated and resting Kv1.2 channels (5). (b and e) Averaged electrostatic potential profiles for each conformational state for selected charge imbalances. (Dotted ellipse) T1 domain. (c) V_m(q_exc,sol) data (dots) for each trajectory frame. Fits by Eq. 3 give C_mp,down = 214.3 ± 0.4 zF, q_exc,p,down = 4.31 ± 0.005 e, C_mp,up = 209.2 ± 0.4 zF, and q_exc,p,up = 3.36 ± 0.005 e, thus revealing a gating charge of 0.95 ± 0.01 e for Ci-VSP. (f) For Kv1.2, C_mp,rest = 736 ± 1.6 zF, q_exc,p,rest = 24.9 ± 0.005 e, C_mp,act = 702 ± 1.3 zF, and q_exc,p,act = 14.84 ± 0.005 e yield a gating charge of 10.1 ± 0.01 e. (Dashed lines) Fits to calculated potentials (data not shown) when excluding the charge of the indicated residue (used in Fig. 3).

Fig. 2, b and e, depicts averaged electrostatic potential profiles at varying ionic charge imbalances, and Fig. 2, c and f, provides the corresponding charge titration plots for the two proteins in their resting and activated states. This analysis yields a gating charge of 0.95 ± 0.01 e for Ci-VSD, and of 10.10 ± 0.01 e for Kv1.2. These values are in good agreement with experimental values (42, 44, 45). Ci-VSD gating charges, as determined by fitting the voltage dependence of time-integrated gating currents using either a Boltzmann relationship or a five-state model, are scattered around one elementary charge (1.10, 1.26, and 1.41 e) (42, 45). Similarly, gating charges of individual Kv1.2 channels were obtained by limiting slope analysis (9.6 e), as well as by normalizing macroscopic gating currents to the number of channels determined through noise analysis (9.96 e) (44).

The Kv1.2 analysis illustrates a further advantage of our charge titration method. Previous MD-based gating charge calculations assumed constant total protein/bilayer capacitances (14, 16, 17, 18). However, our method reveals that the large conformational changes of the channel upon activation result in a decrease in the total capacitance of ∼5%; as the simulation systems used here are larger than those commonly used, the change in C_mp,λ in smaller systems could be even more significant. By fitting both q_exc,p,λ and C_mp,λ (Eq. 3), we prevent any possible bias in the Q_g estimate due to changes in membrane/protein dielectric properties.

We then investigated the influence of individual residues on Q_g by neutralizing individual side chains, i.e., by excluding them from the charge integral in Eq. 2. This approach determined the contribution of every individual amino acid to the total gating charge (Fig. 3; Data S1 and S2). As an internal control, we calculated the cumulative sum of per residue contributions—starting with the gating charge contributions of the non-protein part of the system, e.g., solvent and the membrane—and found these values to converge to the total Q_g of the full system (Fig. 3, a and c). As expected, the most prominent positive contributions came from residues located at the S4 segment.

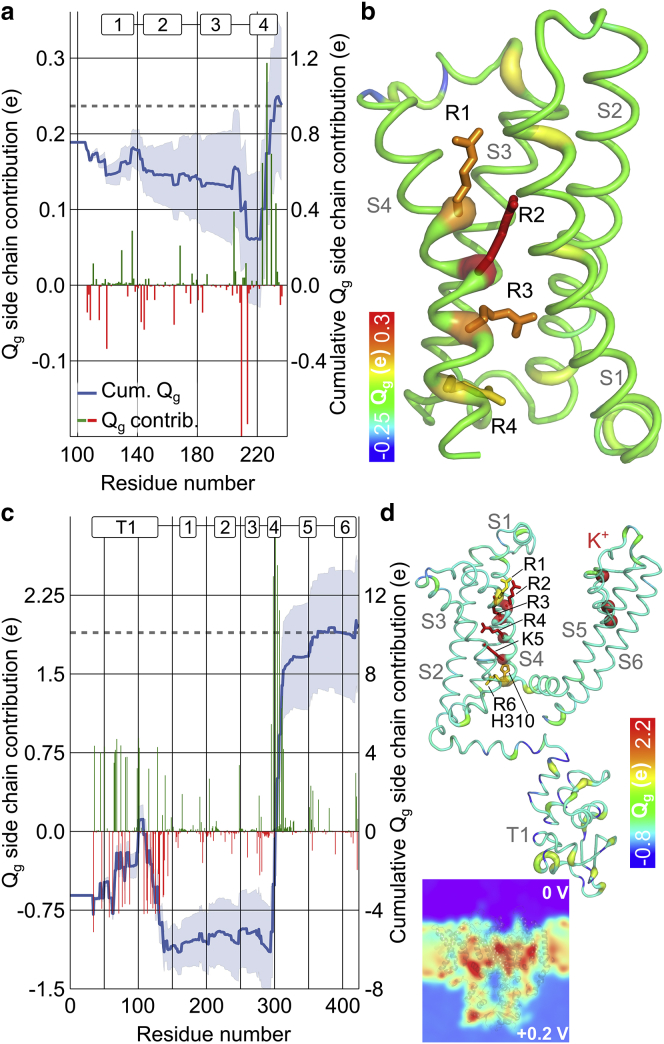
Figure 3.

Contributions of individual residues to the gating charge. (a and c) (Left y axis) Gating charge contributions of all side chains (green, positive; red, negative) confirm the prominent influence of the S4 segments in (a) Ci-VSD and (c) Kv1.2. (Right y axis) Cumulative sums of gating charge contributions (blue line) converge to the total gating charge (gray, dotted line) within statistical error (SD, blue shaded area). The cumulative sums start at the contribution from non-protein charges (e.g., membrane). (b and d) Molecular illustration of side-chain contributions to the gating charge in putty representations of (b) Ci-VSD and (d) a Kv1.2 monomer. Contributions are indicated by the tube thickness and color-code. Side chains with a contribution >10% of total Q_g are shown as sticks. (Inset) Slice through an electrostatic potential map of an activated channel in the membrane.

Kv1.2 voltage sensing is modulated by the T1 domain

The Kv1.2 channel has a large cytoplasmic T1 domain that is expected to reside outside of the electric field. During equilibration of the Kv1.2 simulation systems, in both the activated and the resting state, we reproducibly observed conformational rearrangement of the T1 domain and the T1–S1 linker relative to the transmembrane part of the channel, in which the T1/linker approached the lipid bilayer, assisted by the transient formation of salt bridges between both parts of the channel (Fig. S3, a and b). Comparison of the equilibrated resting and activated conformations demonstrates an upward movement of ∼3 Å of the T1/linker during channel activation (Fig. S3 c). Moreover, the T1 domain can sense a small fraction of the transmembrane field (Figs. 2 e and 3 d, inset), and the T1 domain, including the T1–S1 linker, contains a total charge of −5 e per monomer. Movement of these charges within the electric field results in a contribution of ∼−0.6 e per monomer by the T1/linker to the total Q_g (Fig. 3 c; Data S2). Earlier electrophysiological experiments demonstrated point mutations in T1 cause voltage-dependent rearrangements of this domain and changes in the apparent Q_g in Kv1.2 (46, 47, 48). Our new analysis shows that the T1 domain could affect K⁺ channel voltage sensing at least partially by directly modifying the gating charge.

Voltage-dependent Na⁺ binding to the glutamate/aspartate transporter Glt_Ph

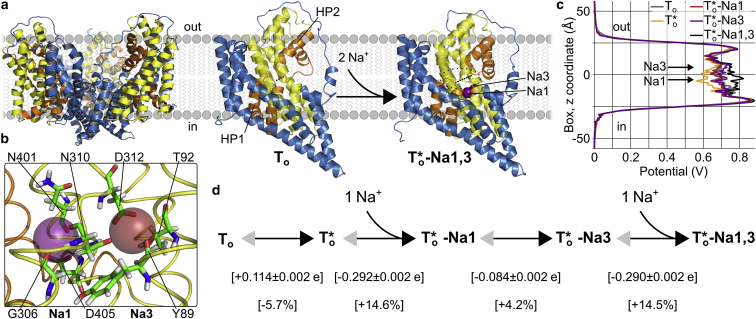
Glutamate is the major excitatory neurotransmitter in the mammalian central nervous system. Excitatory amino acid transporters (EAATs) mediate secondary active transport of glutamate or aspartate across the cell membrane by coupling it to the cotransport of three Na⁺, and one H⁺, and to the antiport of one K⁺ (49). This stoichiometry results in the net inward movement of two positive elementary charges per transported glutamate. Na⁺ binding is a crucial determinant of glutamate or aspartate association to its binding site and substrate translocation. In the apo outward-facing state, the external hairpin HP2 is closed, preventing glutamate/aspartate association (35, 38). The initial binding of two Na⁺ ions (the Na1 and the Na3 ions) induces or stabilizes HP2 opening (35, 50), such that glutamate can subsequently bind (51, 52) (Fig. 4 a). The bound substrate induces closure of HP2 (51), which is stabilized by the final binding of the third Na⁺ (the Na2 ion). When HP2 is closed, the fully bound transporter can translocate to the inward-facing conformation (53).

Figure 4.

Voltage dependence of initial Na⁺ binding to glutamate transporters. (a) (Left) structure of a Glt_Ph trimer and its position in the membrane. (Right) Outward-facing Glt_Ph monomers in the apo (T_o) and sodium-bound (T^∗_o−Na1,3) conformations (PDB: 4OYE and 4OYF; blue, static trimerization domain; yellow/orange, transport domain; star, open HP2). Dashed lines indicate the distance between hairpins HP1 and HP2 and highlight HP2 opening, which is promoted by Na⁺ binding and enables subsequent association of the neurotransmitter to its binding site (indicated by the dotted ellipse). (b) Close-up of the Na⁺ binding sites Na1 and Na3 in T^∗_o−Na1,3 in Glt_Ph. (c) Electrostatic potential profiles from single-bilayer simulations in the respective states. (d) Calculated gating charges for HP2 opening and subsequent Na1 and Na3 binding (upper row, gating charges of each transition per Glt_Ph monomer; lower row, percentage of the total charge movement per transport cycle, −2 e).

Whereas Na2 binds after the neurotransmitter, Na1 and Na3 need to be occupied in advance to initiate the transport cycle and thus represent the key binding sites that mediate Na⁺-dependent gating of the substrate binding site (35). Because initial Na⁺ binding promotes HP2 opening and primes the transporter for substrate binding, the voltage dependence of Na⁺ binding and Na⁺-associated conformational changes before glutamate association defines the efficiency of EAAT transporters to capture the free neurotransmitter (54, 55). Recently, a novel crystal structure of a prokaryotic homolog, Glt_Tk, allowed localization of all Na⁺ binding sites (38) (Fig. 4 b). Comparison of apo and Na⁺-only bound crystal structures shows that initial Na⁺ binding is coupled to HP2 opening (35); however, it is unclear if this conformational change occurs before or after binding of the Na1 and Na3 ions. In microsecond-long MD simulations of outward-facing apo Glt_Ph (that is, before spontaneous Na⁺ binding events), HP2 mainly assumed a closed conformation, as in the apo crystal structure; but spontaneous, reversible HP2 openings—as in the Na⁺-only bound structure (35)—were reproducibly observed. In contrast, the Na⁺-only bound Glt_Ph structure resides in its HP2-open conformation in MD simulations (data not shown). We thus hypothesize that Na⁺-associated HP2 opening occurs via a conformational selection mechanism, where binding of Na⁺ ions stabilizes HP2 in its open state: HP2 opens spontaneously and permits Na⁺ binding to the Na1 site. This Na⁺ ion then hops to the Na3 site; followed by binding of a second ion to the Na1 site. Such a Na⁺ binding sequence was first proposed by Huang and Tajkhorshid (56) and further corroborated by Bastug et al. (37).

We constructed single-bilayer simulation setups of Glt_Ph in these states and observed reproducible changes of the transmembrane potential profile within the electric field across the membrane, suggesting that each partial reaction is electrogenic (Fig. 4 c). To further quantify the voltage dependence of Na1 and Na3 binding, we performed gating charge calculations as described above. Fitting the charge titration plots for the four consecutive processes permitted the assignment of a gating charge of +0.114 e to HP2 opening before Na⁺ binding. Subsequent Na⁺ binding to Na1 confers −0.292 e, and its translocation from Na1 to Na3 −0.084 e. The binding of an additional Na⁺ to Na1 results in a doubly occupied transporter and is again associated with the transfer of −0.290 e (Fig. 4 d). In total, HP2 opening and binding of Na1 and Na3 are thus associated with a charge transfer of ∼−0.55 e. The voltage dependence of Na⁺ binding has been experimentally determined by direct measurements of EAAT2-associated charge movements and by voltage-clamp fluorometry on EAAT3 to be in the range of −0.4 to −0.5 e (57, 58, 59). In all experimental studies, single Boltzmann functions have been used to quantify this process, which is expected to slightly underestimate the true voltage dependence. These experiments are thus in good agreement with our gating charge calculations.

Discussion

Voltage-dependent changes in protein function are essential for electrical signal generation and propagation, and regulate many other cellular processes. Thus far, the molecular mechanisms of voltage sensing have mainly been studied using a combination of site-directed mutagenesis and electrophysiological recordings, including sophisticated techniques such as direct measurements of gating currents, noise analysis, and limited slope analysis (1, 2, 3, 4, 60). In many transporters or receptors, substrate binding and translocation contribute to voltage sensing, which can be reliably measured, but the underlying mechanisms are more challenging to be resolved experimentally.

Molecular dynamics-based gating charge calculations permit the direct and efficient assessment of all sources of voltage sensitivity and the contributions of defined groups of atoms such as residues, ligands, or bound ions. While most experiments can only report on the total voltage sensitivity, gating charge calculations can be used to identify functionally relevant and voltage-dependent partial reactions in channels and transporters—which in turn can inform further experiments for validation. In recent years, an increasing number of membrane proteins utilizing noncanonical voltage sensing mechanisms (61, 62, 63, 64, 65) have been reported, and MD simulations can also reliably quantify the gating charge also in these cases. However, all simulations still require structural models of the protein states of interest, and the reliability of the insights from gating charge calculations depends on the quality of the input model. We assume the combination of experiments and computational gating charge calculations to be the most efficient way to obtain a complete understanding of the voltage sensing mechanisms in biological membrane proteins.

We here describe computational charge titration using CompEL all-atom MD simulations to calculate gating charges. CompEL permits membrane protein simulations with electrochemical gradients under most realistic conditions and permits optimal determination of the V_m(q_exc,sol) relationships. CompEL enables the user to easily set up multiple charge titration simulations in presence of different ionic charge imbalances for reliable statistical evaluation of the fit. Because the capacitance is treated as a second state-dependent variable, the method can generally be applied to all kinds of membrane proteins. This implies another advantage for the user, because the simulation setups for the different protein states do not need to be of identical atomic composition, and might even be reused from other projects. Although the use of classical MD implies simplifications, e.g., lack of polarizability and fixed protonation states, the agreement of our and other MD data with experiments shows that this falls within acceptable levels. However, such features could be easily provided by alternative force fields and extensions to the MD code.

Before the introduction of CompEL (19, 20), another approach had been developed to enable simulations of single-bilayer MD systems under electrochemical gradients using an artificial vacuum slab to split the aqueous compartment into two parts (66). Treptow et al. (17) applied this vacuum slab technique to gating charge calculations on Kv1.2. In this work, the V_m(q_exc,sol) relationships have been derived from two simulations with different charge imbalances with the channel in two states to estimate the gating charge. A potential drawback of the vacuum slab method is that water evaporation at the air/water interface can induce electrical noise, which can bias the transmembrane potential calculation (41). Furthermore, Treptow et al. (17) focused on an initial partial deactivation transition of Kv1.2, and based on these simulations, the authors concluded that the total membrane/protein capacitance remains constant upon the conformational transition of the channel (17). Therefore, the gating charge calculations in this and subsequent studies on Kv1.2 assumed constant capacitance (14, 17). In contrast, for the full deactivation transition of Kv1.2, we observe a statistically significant increase in the total capacitance of ∼5% upon deactivation. Because the conformational changes of the channel are rather large, such a capacitance change is not unexpected. It depends on the protein density in the membrane, and is thus not detectable in electrophysiological experiments. However, to obtain an unbiased estimate of the gating charge from MD simulations, it is crucial to treat the capacitance as a second state-dependent variable. This also applies to another gating charge calculation method that—as opposed to analyzing V_m as a function of applied charge imbalances—analyzes the amount of charge transferred upon the conformational transition, the so-called displacement charge, in MD simulations at constant V_m (18). This approach has proven useful (15, 16), but its general applicability is again limited by its underlying assumption of constant membrane/protein capacitance.

We furthermore describe an efficient approach to estimate the fractional contributions of individual amino acids to the total Q_g by investigating the effects of excluding these partial charges from the charge density for the electrostatic potential calculation. Several earlier studies employed another method: The fractional contribution of an individual residue to the total Q_g is given by the change in electrical distance upon the gating transition multiplied by the partial charges of this residue. The electrical distance was determined by evaluating the dependency of the local electrostatic potential at this residue on V_m (14, 17, 18); this method thus requires knowledge of the electrostatic potential distribution in three dimensions. In contrast, our charge-exclusion approach evaluates the effect of charge neutralizations on V_m and therefore only requires a one-dimensional potential profile, which is expected to converge faster and thus provide higher statistical accuracy (Fig. S1). The underlying linear decomposition of the charge contributions represents a simplified treatment of the interactions between individual residues and the rest of the system. We tested for potential influences of this simplification in MD simulations of S4 mutations in Ci-VSD that demonstrated a reasonable approximation of the gating charge contributions (Fig. S2). Thus, the charge-exclusion approach determines the contributions of all constituents of the membrane protein system such as amino acids, lipids interacting with the protein, ions, or ligands, for just a few minutes of additional computer time required to reintegrate the charge densities upon charge exclusion.

The double-bilayer setup—and thus the use of two identical copies of the same protein—appears at first glance computationally inefficient. This is not true. The presence of two identical proteins leads to twice as much sampling per simulation time. Thus, less total simulation time is required for the V_m(q_exc,sol) relationship to be converged (Fig. S1 b). As commonly done in biomolecular simulations, we evaluate long-range electrostatics by the particle mesh Ewald (PME) method, which scales with an N⋅log(N) relationship, where N is the number of particles. Thus, PME could result in a slight computational overhead when calculating gating charges with CompEL. However, this effect is negligible (because it just applies to the fast Fourier transformation calculations of PME, which represent ∼10% of the computational time needed for one time step in GROMACS) and is usually fully overcompensated by the increase in parallel efficiency of the larger CompEL simulations systems on modern hardware (20). For the initial single-bilayer setups of Kv1.2 or Ci-VSD, we typically achieve simulation performances of ∼36 or 185 ns/day on a single computer node equipped with two standard multicore CPUs and two high-end consumer-class GPUs (67) (see Materials and Methods). In practice, a few hundreds of nanoseconds may be initially required for the equilibration of the simulation systems, followed by a few CompEL charge titration simulations for just a couple of nanoseconds, which is typically sufficient to reach acceptable statistics (Fig. S1 b). Thus, the computational requirements are relatively modest, and even users without access to high-performance computing clusters might be able to conduct the gating charge calculations on just one or two modern desktop computers.

Conclusions

Advances in structural biology have provided high-resolution structures for multiple membrane proteins that now have to be linked with functional data. At present, only a few characteristics of channels, transporters, and receptors can be used for such comparisons. Transport rates are often difficult to obtain experimentally and in simulations, while differences in ionic conditions, membrane background, and force-field inaccuracies make comparing binding affinities and pharmacological signatures problematic. In contrast, voltage-dependent changes in protein function can be easily and reliably quantified for channels, transporters, and receptors in electrophysiological experiments. Computational charge titration by CompEL simulations, as a method to calculate gating charges of voltage-dependent proteins, provides the opportunity to quantify the voltage dependence of multiple individual protein functions for comparison with experimental data. We believe that this approach will not only be useful for further understanding voltage sensing and gating in atomistic detail, but also to test the correctness and biological significance of existing and future structural models by validating theoretical gating charges with experimental results.

Author Contributions

J.-P.M. conceived the project; J.-P.M., R.B., and C.F. designed research; J.-P.M., C.A., and R.B. carried out simulations and analyses; B.L.d.G. advised on theory development and simulation design; and all authors wrote the article.

Editor: Jose Faraldo-Gomez.

Supporting Material

Data S2. Spreadsheet Containing the Gating Charge Contributions for All Residues in Kv1.2, including All Fit Parameters

Gating charges are given per tetramer.