Abstract
Allostery pervades macromolecular function and drives cooperative binding of ligands to macromolecules. To decipher the mechanisms of cooperative ligand binding it is necessary to define at a microscopic level the structural and thermodynamic consequences of binding of each ligand to its allosterically coupled site(s). However, dynamic sampling of alternative conformations (microstates) in allosteric molecules complicates interpretation of both structural and thermodynamic data. Isothermal titration calorimetry has the potential to directly quantify the thermodynamics of allosteric interactions, but usually falls short of enabling mechanistic insight. This is because 1) its measurements reflect the sum of overlapping caloric processes involving binding-linked population shifts within and between microstates, and 2) data are generally fit with phenomenological binding polynomials that are underdetermined. Nevertheless, temperature-dependent binding data have the potential to resolve overlapping thermodynamic processes, while mechanistically constrained models enable hypothesis testing and identification of informative parameters. We globally fit temperature-dependent isothermal titration calorimetry data for binding of 11 tryptophan ligands to the homo-undecameric trp RNA-binding Attenuation Protein from Bacillus stearothermophilus using nearest-neighbor statistical thermodynamic models. This approach allowed us to distinguish alternative nearest-neighbor interaction models, and quantifies the thermodynamic contribution of neighboring ligands to individual binding sites. We also perform conventional Hill equation modeling and illustrate how comparatively limited it is in quantitative or mechanistic value. This work illustrates the potential of mechanistically constrained global fitting of binding data to yield the microscopic thermodynamic parameters essential for deciphering mechanisms of cooperativity in a wide range of ligand-regulated homo-oligomeric assemblies.
Introduction
Allostery is ubiquitous in regulated cellular processes and is an important consideration in the design of artificial ligands for therapeutics, or for engineering novel functions (1, 2, 3, 4). Its hallmark is the observation that ligand binding is altered by binding of one or more additional ligands at distant sites in the same target. In the case of homotropic allostery, i.e., when the ligands are the same, it is commonly diagnosed from binding curves that are fit poorly by a standard Langmuir isotherm (5, 6). Although such curves (sigmoidal, in the case of positive cooperativity) can be diagnostic, the common practice of fitting such data with the Hill equation provides an unintuitive coefficient with limited to no mechanistic value (7, 8). The next level of sophistication in modeling binding data is to define a binding polynomial that assigns a distinct set of thermodynamic parameters for each discernable ligand binding event. The venerable “concerted” MWC and “sequential” KNF models (9, 10) are two such formalisms that can successfully predict cooperative behavior in many allosteric systems. While more informative than Hill equation modeling, the resulting set of thermodynamic constants imperfectly captures the mechanism and magnitude of allosteric communication (4, 11). On the other hand, if a specific mechanistic binding model is known or can be appropriately posed, fitting the data with polynomials derived from such mechanisms has the potential to provide the level of precision required to understand allosteric communication at the microscopic level.
Isothermal titration calorimetry (ITC) has emerged as the premier technique for probing the thermodynamics of bimolecular interactions, both independently and when combined with complementary methods (12, 13, 14). ITC directly measures the enthalpy change (ΔH) resulting from binding of a ligand to a macromolecule; fitting the data with an appropriate binding model yields the overall free energy change ΔG via the equilibrium association constant KA (15, 16). In addition, the temperature dependence of ΔH yields the change in heat capacity (ΔCp), which is typically dominated by changes in the system’s hydration state, but also reflects macromolecular degrees of freedom, and thus can provide information about structural perturbations (17, 18, 19). Cooperativity affects each of these measurable values, because binding of successive ligands to a macromolecule with multiple binding sites may occur with higher or lower affinity, be more or less enthalpic, and be associated with different degrees of structural remodeling (13, 20, 21). Despite its strengths, ITC analyses often fall short of providing mechanistic detail, in part because its bulk thermodynamic measurements reflect the sum of simultaneous binding-coupled caloric processes that arise from population shifts between the microstates of the system, and because thermograms are generally fit with phenomenological multiparameter binding polynomials that are underdetermined (12, 13, 20, 21). Indeed, because the thermograms are affected by both ΔH and KA, positive and negative cooperativity can yield strikingly similar thermograms (e.g., Fig. S1 in the Supporting Material).
As a paradigmatic model of homotropic and heterotropic allostery, cooperativity in the ring-shaped homo-undecameric (11-mer) trp RNA-binding Attenuation Protein (TRAP) (Fig. 1 A) has been a matter of interest since the discovery of its function and quaternary structure (22). In many species of bacilli, TRAP regulates expression of the trp operon through RNA binding activity that is allosterically regulated by binding L-tryptophan (Trp) to its 11 structurally identical sites located at its subunit interfaces (Fig. 1 B). Nuclear magnetic resonance (NMR), proteolytic, and crystallographic data (23, 24) indicate that in its Trp-free “apo” state loops in TRAP that shield its binding sites from bulk solvent are dynamic and structurally heterogeneous. This disorder has been proposed to simultaneously mask its RNA binding surface, and to allow gated access by Trp, whereas the loops rigidify upon Trp binding, stabilizing the architecture of the RNA binding surface of TRAP (23, 25). By virtue of the binding-coupled structural changes and close proximity of adjacent Trp binding sites (separated by one β-strand), cooperativity in Trp binding to TRAP is expected, although thermodynamic and kinetic measurements to date have yielded seemingly contradictory conclusions regarding its presence, magnitude, or sign (i.e., cooperative, noncooperative, or anticooperative) (24, 25, 26, 27, 28).
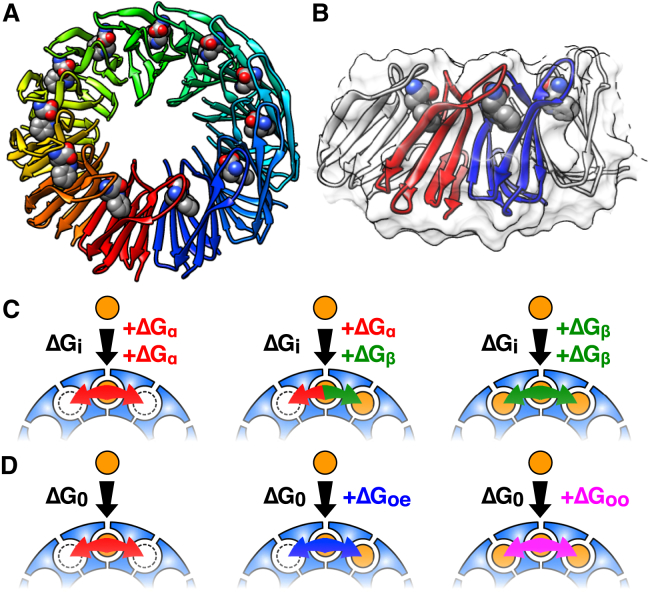
Figure 1.
TRAP is a biosensor with 11 equivalent binding sites for tryptophan. (A) Crystal structure of Trp-bound TRAP11 (26); bound Trp are shown as spheres. (B) Closeup of two neighboring protomers in the crystal structure (red and blue) showing proximity of bound tryptophan molecules. (C) NN-a model of cooperativity between sites, in which binding free energy is the sum of an intrinsic free energy ΔGi plus coupling to either empty (ΔGα) or occupied (ΔGβ) neighboring sites. (D) NN-na model, in which binding to a site flanked by two empty sites has a reference ΔG0, modified by coupling free energies when the site is flanked by one or two occupied neighbors (ΔGoe, ΔGoo), respectively. To see this figure in color, go online.
To obtain mechanistically informative parameters, ITC thermograms should be fit with a binding polynomial equation representing a suitable binding model. In the case of TRAP, with 11 potential binding sites for Trp, each of which could either be empty or occupied, there exist 211 = 2048 possible Trp-TRAP configurations. The 11-fold symmetry of the TRAP11 rings result in structural and therefore thermodynamic degeneracy (e.g., the 11 configurations with one bound Trp are structurally identical), leaving 125 unique Trp-TRAP configurations. If each of these configurations were to have unique thermodynamic profiles (i.e., their own ΔH, KA), quantifying them by fitting the ITC thermograms to such a multiparameter phenomenological binding polynomial would certainly not yield meaningful values, despite the often-oversampled nature of ITC data (29).
A reduction in the number of parameters in a complex binding polynomial can be achieved by applying a model that mechanistically relates the energetics of the system from the first ligand binding event to the last (30, 31). Such a model based on Ising lattices (32) was previously proposed by Saroff and Kiefer (33) to describe Trp-TRAP equilibrium dialysis data by posing that the binding affinity of a given site is modulated by additive contributions from the closest neighboring sites; i.e., those to the left and right flanking sites in the TRAP ring (Fig. 1 B). Although in that instance a single set of binding data was apparently insufficient for convergence to a unique set of parameters, such an approach is also compelling because it provides a clear mechanistic basis for quantifying the energetic interactions between sites.
To quantify cooperativity in Trp binding to TRAP, we recorded ITC data over a range of temperatures (which alter the thermograms through its effect on ΔH and KA), and the resulting data were globally fit using binding polynomials derived from: 1) a minimal phenomenological model, 2) a partition function arising from the additive Saroff and Kiefer (33) nearest-neighbor (NN) statistical thermodynamic model, or 3) a partition function from a nonadditive variant of this NN model. Our findings reveal unique heat capacity changes ΔCp for each binding mode, allowing us to deconvolute ΔH and ΔG values for overlapping binding events, thereby distinguishing the two alternative NN models of cooperativity. With the partition function thus defined and parameterized, it is possible to itemize the populations and energies of all states of the system at arbitrary concentrations and temperatures, thus illuminating the Trp-TRAP activation pathway. When paired with structural information, the resulting microscopic thermodynamic values constitute a quantitative basis for a detailed understanding of the mechanism of allostery.
Materials and Methods
Mutagenesis, expression, and purification of Bacillus stearothermophilus A28I TRAP was performed as described in McElroy et al. (23) and Kleckner et al. (25). HPLC-purified and refolded Trp-free (apo) TRAP was dialyzed against sodium phosphate binding buffer: 100 mM NaCl, 50 mM NaPO4, pH 8.0 at 25°C, 0.02% NaN3. The resulting solution was 6.818 ≥ 0.181 μM TRAP11 (75 ± 2 μM binding sites), with concentration measured using UV absorbance at 280 nm with ε = 2980 M−1 cm−1, calculated using the tool ProtParam (34). Trp solutions were prepared by adding solid L-tryptophan (USB Corporation, Cleveland, OH) to buffer matched to the TRAP stock via dialysis, to concentrations of 610 or 765 μM based on a starting stock of 2030 ± 43 μM quantified by UV absorbance at 278 nm with extinction coefficient ε = 5579 M−1 cm−1 (27). Because accurate concentrations are essential for analysis, all samples were prepared from their respective stock with dilution factors measured using an analytical balance precise to 100 μg.
All isotherms were recorded on a MicroCal VP-ITC (Malvern Instruments, Malvern, Worcestershire, UK). Experiments acquired at 20, 35, 40, and 45°C were performed by an initial 3 μL injection followed by 56 × 5 μL injections of 610 μM Trp into 75 μM TRAP. Isotherms at 55 and 65°C were performed using 95 × 3 μL injections of 765 μM Trp into 75 μM TRAP. A reference power of 30 μcal/s and a stirring speed of 300 rpm were used throughout. The reference cell solution was deionized water. The resulting raw differential isotherms were baseline-corrected and integrated using the default ORIGIN routines provided by the manufacturer (35). For both sets of titrations, the first injection point was not fitted.
We implemented a custom ITC data fitting library, “itcsimlib”, to numerically optimize the desired parameters of the various binding models, which were compiled separately as shared libraries. At each step during parameter optimization for the additive and nonadditive statistical thermodynamics models, the predicted free energies and enthalpies were calculated for each of the 2048 (211) TRAP+nTrp configurations. Because each site of TRAP can exist in either a Trp-bound or unbound state, the 2048 possible configurations can be represented by the 11-digit binary representation of the configuration’s index number, such as 00000000000 for the reference state of apo TRAP at index 0, 11111111111 for index 2047 of holo TRAP, 01111100100 for configuration index 996 containing six bound tryptophans, etc. For each configuration index i, its characteristic aggregate ΔGi will be the sum of the individual microscopic binding site free energies ΔGj of the 11 active sites in that configuration:
| (1) |
where ΔGj depends upon the specific model and the occupancy state of the neighboring (j+1 or j−1) sites. In all cases, the configuration is treated as a circular array. ΔHi is obtained in the same fashion as ΔGi, except by summing the characteristic enthalpies ΔHj.
The absolute probability (Pi) of each configuration at a given concentration of free Trp ligand [L] can be obtained from the relative probabilities Ri, which themselves are obtained from the configuration’s ΔGi and the Boltzmann distribution:
| (2) |
where ni is the number of Trp bound to that configuration.
At each of the ITC titration points, the free ligand concentration [L] is not a priori known, but is obtained from the mass balance equation by minimizing the discrepancy between the known total Trp concentration Lt at each titration point and the predicted total ligand concentration, which consists of the free Trp and bound to TRAP, where Mt is the total concentration of the TRAP oligomer macromolecule:
| (3) |
This is achieved in itcsimlib by iterative, numerical minimization of ΔLt by optimization of [L] using the GNU scientific library’s implementation of Brent’s method (36, 37), with [L] = Lt and [L] = 0 as initial bracketing guesses. When this method has converged to a ΔLt of <1 nM, the final probabilities are retained for the evaluation of total enthalpy. Determination of the total heat Q present in the system at injection k can then be obtained at each titration point:
| (4) |
where V0 is the working volume of the ITC cell and ΔHi has been previously calculated for each configuration as described. The heat is normalized by the amount of ligand injected (ΔVkL0).
Analysis requires correction for the volume injected from the titration syringe, which both dilutes the existing solution and displaces an equal volume into the cell stem. Because stirring is continuous during each injection, solution displaced into the cell stem no longer comprises the working volume and only partially contributes to the heat sensed by the instrument (35). Therefore, both the actual and effective dilution of the components must be considered to avoid systematic overestimation of the heat evolved or consumed by the system. Although there are several methods in the literature for calculating this dilution (20, 21), the method recommended by the manufacturer of the VP-ITC instrument is used in itcsimlib (35):
| (5) |
where k is the number of the current injection and Lt0 is the hypothetical concentration of ligand, assuming that all of the injected ligand remains in the cell. ΔVk is the total change in volume as it is the sum of the injected volumes up to Vk, and V0 is the actual working volume of the cell (1.4166 mL for the VP-ITC).
During the ITC experiment, the change in enthalpy of the system is measured at each titration point, and the aforementioned effect of displacement from the working volume must be taken into account. Using the method described above, the displaced material contributes ∼50% as much heat as the equivalent material in the working volume (35):
| (6) |
where Qk is the total calculated heat at the current injection, and Qk−1 is the calculated heat at the previous injection. The resulting ΔQk can be directly compared to the integrated measurements of differential heat obtained from the instrument through a χ2 goodness-of-fit metric for each experiment:
| (7) |
Because uncertainties in the calculated heat can be distorted by the normalization to injected ligand concentration as well as errors in baseline determination, the uncertainty σ2 for each experiment was estimated in itcsimlib by fitting a first-order Savitsky-Golay smoothing spline with a seven-point window to the experimental ΔQ values and calculating the standard deviation of the values from the spline. Confidence limits in optimized model parameters were estimated using two methods: Bootstrapped uncertainties were generated by refitting 200 synthetic datasets composed of the original fit to which randomly selected residuals were “added” with the original parameters to which a 10% variance was applied (38). Chi-square boundary uncertainties were obtained by incrementing an individual parameter above and below its best-fit value while optimizing the remaining model parameters until the resulting goodness-of-fit χ2 exceeded the best-fit χ2 plus the expected variance for the fitted data points (39, 40).
Numerical optimization used the Powell algorithm (41) exclusively, although other optimization algorithms were also evaluated in itcsimlib. For the initial grid fits used to reduce parameter space, the starting values for parameters not explicitly restrained by the grid were initially set to those obtained from a global fit using a phenomenological one-mode model. Figures are generated using gnuplot (42) and matplotlib (43) routines implemented in itcsimlib.
Results and Discussion
Substoichiometric binding conditions are important for discerning allostery
Previously, we performed ITC experiments of Trp binding to wild-type TRAP from the thermophile B. stearothermophilus (Bst) and found the data fit well to a single-site binding model, implying no homotropic cooperativity (27), a finding at odds with results obtained with the mesophile B. subtilis (Bsu) TRAP (44), as well as intuition based on the structure of TRAP (Fig. 1) (26) and the role of coupled folding in its activation (25). However, those ITC experiments were not designed to assess cooperativity; instead they were designed to accurately measure the net ΔCp to quantify the degree of folding resulting from Trp binding (27). By performing the ITC experiments at higher c values (c = [TRAP]Total/Kd), uncertainty in measured ΔH is minimized, but the existence of different binding modes may be missed (15, 45, 46) (Fig. S2). Using lower c values, we observed that ITC titrations of wild-type TRAP do exhibit multiple binding modes, as do titrations with Bsu TRAP (44) (Fig. S3). For these experiments, we utilize the Bst TRAP mutant A28I to enable direct comparison to existing kinetic and NMR data (23, 25). This mutation introduces an additional NMR probe in one of the gating loops above the Trp binding site, and is fully functional in Trp and RNA binding (25, 27, 28).
NN models of Trp-TRAP
Considering that Trp binding to sites on distant parts of the TRAP ring (i.e., farther than one binding site, or ∼25 Å; Fig. 1 A) are less likely to be thermodynamically coupled than the adjacent sites, a nearest-neighbor (NN) model makes the simplifying assumption that interactions between neighboring sites dominate binding thermodynamics (33). Importantly, an NN model reduces the number of potentially energetically distinct binding modes, and allows them to be described by combinations of just a few microscopic thermodynamic parameters.
To automate bookkeeping when generating partition functions encompassing the 2048 (211) possible configurations of TRAP11+0–11 Trp, we represented the TRAP11 ring as a circular one-dimensional array of zeroes or ones (e.g., 00000000000 for apo TRAP, 11111111111 for fully loaded TRAP, and 01100100000 for one of the 165 possible configurations with three bound Trp), then applied systematic rules from the NN formalisms to each configuration to obtain their energy terms. Two NN models of cooperativity were considered, which differ in whether interactions with neighboring sites are additive.
Additive NN model
An additive statistical thermodynamic model of cooperativity can be obtained from the application of occupied and unoccupied (+/−) interactions to the circular TRAP Ising lattice, and has been described previously to interpret experimental TRAP+Trp equilibrium dialysis data by Saroff and Kiefer (33). In this model, Saroff and Kiefer (33) proposed an intrinsic free energy (ΔGi) of Trp binding that is modulated by coupling to neighboring unoccupied (ΔGα) or occupied sites (ΔGβ). By inspecting each of the 11 binding sites and its immediate neighbors for each of the 2048 possible TRAP+nTrp configurations, aggregate free energies can be determined, yielding a partition function composed of 32 energetically distinct configurations whose energies depend on the concentration of free Trp W. Because of the relation between the binding free energy and equilibrium binding affinity, ΔG = RT ln(K), the intrinsic affinity Ki arises from the free energy ΔGi, while the multiplicative coupling coefficients α and β are obtained from the coupling free energies ΔGα and ΔGβ. By convention, the free energy before ligand binding is defined as the reference state, or zero. The model is additive in that it postulates that the free energy contributions from coupling to neighboring empty or occupied sites simply sum; i.e., the energy of binding to a site with no occupied neighbors is ΔGi+2ΔGα, a site with one occupied neighbor is ΔGi+ΔGα+ΔGβ, and that with two occupied neighbors is ΔGi+2ΔGβ.
By introducing a hypothetical intrinsic affinity Ki for a site with no neighbors, the model of Saroff and Kiefer (33) suffers from mathematical correlation of its parameters. The partition function for this model, composed of three thermodynamic parameters (Ki, α, and β), can be simplified using the identities Kiα2 = K0, and β/α2 = γ2. This has the effect of replacing the abstract intrinsic binding free energy (ΔGi) with a reference free energy of binding, (ΔG0), which is the difference in free energy between the reference unbound state and a Trp-bound site flanked by two unoccupied sites, while ΔGγ is the coupling free energy term. This restatement produces an equivalent partition function (additive nearest-neighbor (NN) model, hereafter referred to as the “NN-a” model) with the following expression with 32 unique energetic terms:
| (8) |
Nonadditive NN model
In addition to the additive model (NN-a), we consider an alternative, “NN-na” model that describes interaction energies between sites as not simply a sum; that is, the coupling free energy from two occupied neighbors is not just twice that of one occupied neighbor. Such behavior could arise, for example, if binding of one ligand reduced local dynamics to such an extent that an additional ligand induces a relatively smaller degree of conformational restriction. Thus, the free energy of binding to a site flanked by 0, 1, or 2 occupied sites becomes ΔG0, ΔG0+ΔGoe, and ΔG0+ΔGoo, respectively (oe, occupied-empty; oo, occupied-occupied, Fig. 1 D). The partition function for this nonadditive model, expressed in terms of the corresponding reference binding affinity K0 and multiplicative factors δ and ε (from ΔG0, ΔGoe, and ΔGoo, respectively), possesses a significantly greater number of nondegenerate energetic states (48 vs. 32; Fig. S11):
| (9) |
Provided one of these NN models can accurately replicate experimental observations, it has the potential to quantify the allosteric site-site coupling that arises from local ligand-dependent changes in the structure and dynamics of the protein.
Itcsimlib framework for ITC data
In a typical ITC experiment, the heat content of the cell is measured as a protein (or ligand) is titrated into ligand (or protein), and is directly related to the enthalpy change (ΔH) of the system (14, 15, 20). The affinity and stoichiometry are subsequently obtained by fitting a binding model to the integrated enthalpies at each titration point. For the NN models considered above, after the Boltzmann probability of each TRAP+nTrp configuration is obtained from its characteristic ΔG, their enthalpies can be assigned in the same way as the free energies by using the parameters ΔHi and ΔHγ for model NN-a, or ΔH0, ΔHoe, and ΔHoo for the NN-na. This parameterization allows the binding enthalpies to differ depending on the occupancy of the neighboring identical sites. To facilitate model analysis, we developed a software library (itcsimlib) for parsing experimental ITC datasets and optimizing the parameters of phenomenological or statistical thermodynamic binding models. Itcsimlib was written in Python and makes extensive use of the SciPy scientific computation library (37). To accelerate computation, the additive and nonadditive statistical thermodynamics models themselves were written in the C programming language. Both components are available for download at http://doi.org/10.5281/zenodo.159716.
Data collection
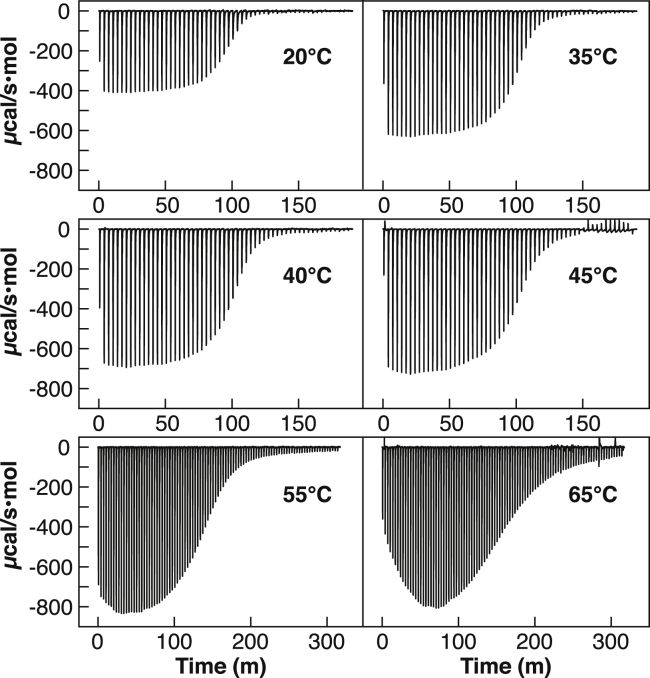
ITC isotherms were obtained by titrating L-tryptophan into 75 μM Bst A28I TRAP at six temperatures: 20, 35, 40, 45, 55, and 65°C (Fig. 2); scanning calorimetry experiments indicate that TRAP denaturation occurs well above these temperatures (27, 44). The resulting integrated enthalpies, ΔHobs, at each titration point were then used as the experimental data for restraining the two statistical thermodynamic models. Individually, each of these experimental datasets could be fit well using a phenomenological model consisting of two independent binding modes. However, in addition to only providing bulk-average descriptions of binding energetics, such a typical analysis neglects the improved precision and insight available by globally fitting across multiple experimental conditions (in this case, temperature).
Figure 2.
Calorimetric isotherms obtained by titrating Trp into TRAP at different experimental temperatures reveal multimode, cooperative binding, with different Kd, ΔH, and ΔCp, although at lower temperatures those features cannot be discerned.
Fitting of ITC data to a phenomenological two-site model
Global fitting of the six datasets was achieved by minimizing the reduced χ2 between the experimental datasets and the fit generated by the model at each of the experimental conditions. This required the consideration of the change in heat capacity associated with binding, ΔCp, and its effects on the temperature dependence of ΔG and ΔH terms. The inclusion of ΔCp is a significant added benefit of global fitting, as it provides structural information, namely on the exclusion (or inclusion) of solvent as part of the binding event, and changes in protein structure (17, 18). For binding processes with a temperature-independent ΔCp, the temperature dependence of enthalpic, entropic, and free energy terms are well defined (18, 19, 47):
| (10) |
First, we performed a global fit of the six experimental isotherms using a derivation of a common (35) phenomenological two-site binding model comprising eight parameters (n1, ΔG1, ΔH1, ΔCp,1 and n2, ΔG2, ΔH2, ΔCp,2). This model describes two independent binding modes with variable stoichiometry n:
| (11) |
where Q is per-molar heat content of the system, Θ is the fractional saturation of each mode, and R is the universal gas constant.
Although this two-site model provided qualitatively acceptable fits to the experimental data (Fig. S4), its mechanistic ambiguity limits interpretation of the resulting parameters (n1 = 2.5, ΔG1 = −9.2 kcal/mol, ΔH1 = −13.2 kcal/mol, ΔCp,1 = +480 cal/mol/K, n2 = 8.2, ΔG2 = −9.3 kcal/mol, ΔH2 = −20.4 kcal/mol, and ΔCp,2 = −650 cal/mol/K). Indeed, the large positive ΔCp,1 of +480 cal mol−1 K−1 is unusual for ligand binding processes (18, 19, 47). However, fitting to this two-site model enables comparison to existing phenomenological observations: specifically, the resulting fits suggest a nominal ΔG of ∼−9.2 kcal/mol for both binding modes, which corresponds to a Kd,obs of 0.4 μM at 40°C, agreeing with previous measurements on both wild-type TRAP and its A28I mutant (27). A model composed of three independent binding modes was also evaluated, but this expansion did not significantly improve fit quality.
Global fitting to NN mechanistic models
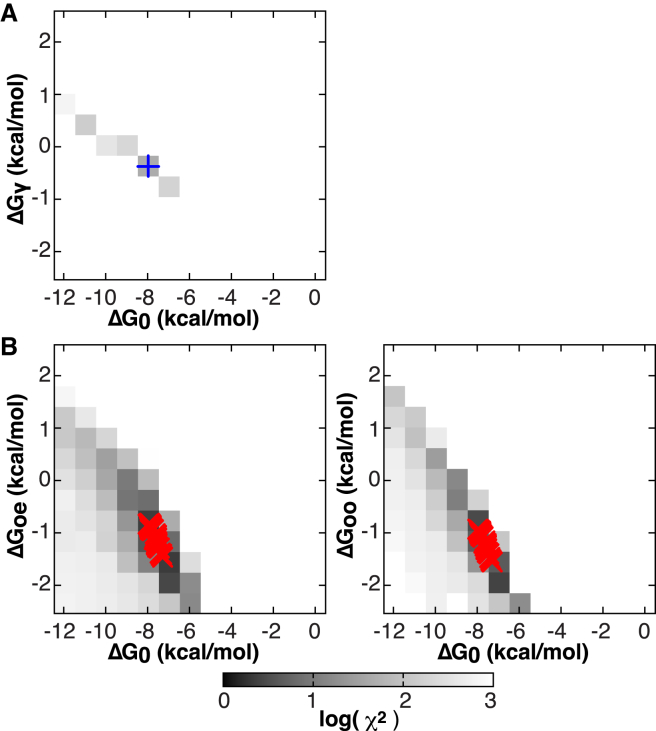
We next compared the ability of the NN models to globally fit the available isotherms. When optimizing models with many parameters against experimental data (48, 49, 50), numerical algorithms can converge to local minima, and/or parameters may be highly correlated, limiting both accuracy and precision (39, 49, 50). To evaluate these issues, the free energy parameters for the proposed statistical thermodynamics models were systematically sampled across several two-dimensional grids: ΔG0 versus ΔGγ for the additive NN-a model (Fig. 3 A), and ΔG0 versus ΔGoe and ΔG0 versus ΔGoo for the NN-na model (Fig. 3 B). The remaining ΔH and ΔCp parameters for each model were then freely optimized.
Figure 3.
Binding free energy parameter grids used to reduce parameter search space and identify χ2 minima. (A) Grid of coupling free energy (ΔGγ) versus the free energy of binding to a reference state with no occupied neighbors (ΔG0), for the six-parameter additive model. (Blue cross) Global minimum. (B) Coupling free energies for the nine-parameter model of nonadditive cooperativity, of sites flanked by one (ΔGoe) and two (ΔGoo) occupied neighboring sites, versus the reference state ΔG0. (Red crosses) Values of fits to 50 random bootstrap datasets were used to estimate parameter uncertainties, using the grid minimum as a starting point. To see this figure in color, go online.
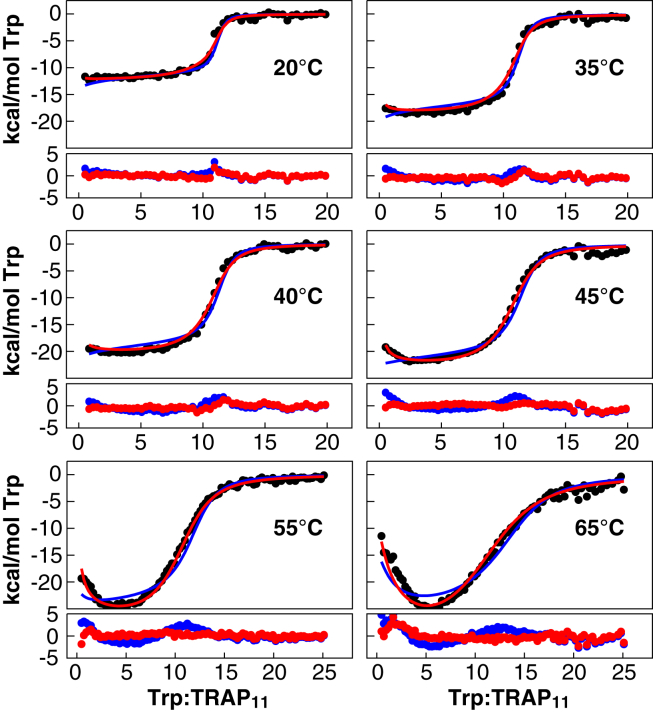
This grid fitting procedure yielded a global χ2 minimum for the six-parameter (two sets of ΔG, ΔH, and ΔCp values) NN-a model, with a reference free energy ΔG0 of −8 kcal mol−1 and coupling free energy ΔGγ of −0.5 kcal mol−1, indicative of weak positive cooperativity (Fig. 3 B; Table S1). However, this model demonstrated relatively poor agreement with the experimental data (Fig. 4; reduced χ2 = 7.1) with residuals that deviate systematically from the observed values both early and late in the titration (Fig. 4).
Figure 4.
Nonadditive nearest-neighbor model provides a superior global fit to experimental data. Integrated enthalpic heats per injection (black circles) at different temperatures are globally fit using the additive model NN-a (blue, χ2 = 7.1) and nonadditive model NN-na (red, χ2 = 1.8). The resulting residuals from each fit are shown below each isotherm. To see this figure in color, go online.
The nonadditive NN-na model, defined by three sets of ΔG, ΔH, and ΔCp values (Fig. 3 C), also yielded an apparent global minimum on the two systematically sampled grids for its ΔG parameters. In addition to these two-dimensional grid fits, the one-dimensional χ2 error surfaces for each of the nine parameters reveal well-defined minima (Figs. S6–S8). After fit convergence, model NN-na provides substantially better agreement to the experimental data (reduced χ2 = 1.8, Fig. 4), and more uniformly distributed residuals. The resulting optimized parameters indicate positive cooperativity (Tables 1 and S2; Fig. S5), suggesting that Trp binding to a site flanked by empty sites occurs relatively weakly (ΔG0 = −8 kcal mol−1 at 40°C; Kd = 4 μM), while having one flanking occupied site stabilizes binding by ∼13% (1 kcal mol−1; Kd = 0.8 μM at 40°C). Finally, binding to a site flanked by two occupied sites is only slightly more favored (15% greater ΔG), with a Kd of 0.7 μM.
Table 1.
Best-fit Parameters for NN-na Model of Trp Cooperativity
| NN | ΔGcoupling |
ΔGbind |
ΔHcoupling |
ΔHbind |
ΔCp,coupling |
ΔCp,bind |
Kd |
|---|---|---|---|---|---|---|---|
| kcal mol−1 | kcal mol−1 | kcal mol−1 K−1 | μM | ||||
| 0 | — | −7.70 ± 0.21a | — | −13.5 ± 1.4a | — | 0.10 ± 0.10a | 4.24 ± 0.12 |
| 1 | −1.04 ± 0.22a | −8.74 ± 0.21 | −6.11 ± 1.0a | −19.7 ± 1.2 | −0.49 ± 0.10a | −0.39 ± 0.10 | 0.80 ± 0.24 |
| 2 | −1.15 ± 0.22a | −8.85 ± 0.21 | −4.67 ± 1.4a | −18.2 ± 1.4 | −0.45 ± 0.11a | −0.39 ± 0.10 | 0.67 ± 0.18 |
Globally fit parameters are given at a reference temperature of 40°C (313.15 K). Confidence intervals were obtained via bootstrapping with 200 replicates. NN, number of occupied nearest neighbors. Unless otherwise indicated, terms were obtained from the sum of the reference state (e.g., ΔG0) and coupling terms (e.g., ΔGoe and ΔGoo). Equilibrium constants from ΔGbind = RT ln Kd at 40°C.
Fitted term.
The best fit parameters for the NN-na model indicate that initial binding to sites flanked by two empty neighbors is enthalpically driven at 40°C, with a ΔH0 of −14 kcal mol−1, and binding to sites flanked by one and two occupied neighbors is stabilized by additional enthalpic effects of −6.1 and −4.7 kcal mol−1, respectively. Correspondingly, at 40°C binding is entropically disfavored, with a ΔS of −18.5 cal mol−1 K−1 for a site with empty neighbors, and −34.7 and −29.8 cal mol−1 K−1 for one and two occupied neighbors, respectively; these reveal a higher entropic penalty to binding to sites with one occupied neighbor, but slightly lower penalty for a site with two occupied neighbors.
Limitations
Implementation of this mechanistic fitting approach has several requirements. First, and foremost, a suitably constrained mechanistic model must be posed such that a binding polynomial can be constructed and tested during global fitting. Second, discrete binding modes must display distinct thermodynamic behavior over experimentally accessible conditions. For temperature-dependent binding data in particular, we would expect that ΔCp values unique to each binding mode would provide the highest resolving power, while also being most mechanistically informative about differences in those binding modes. It follows that successful implementation would depend on those ΔCp values being sufficiently different to generate distinguishable effects on ΔH over experimentally accessible temperature ranges, and being relatively temperature-independent over that range. Lastly, like most multivariate fitting, fitness metrics are better used for comparing alternative models than for establishing whether a particular model is “right”.
Trp binding trajectory
The partition functions for the NN models allow computation of the population of TRAP11+nTrp species at arbitrary concentrations, thus predicting features of the Trp-dependent behavior of TRAP (Figs. 5, S9, S10, and S12). As a consequence of the stabilizing effect of having a bound neighbor, the NN-na model predicts that TRAP species with only one Trp bound are disfavored relative to those with none or two sites bound. In contrast, the small additional benefit to having two bound neighbors does not similarly bias the populations when comparing rings with two versus three bound Trp (Fig. 5). In addition, the most energetically favorable configurations (i.e., those with the lowest free energy), are not necessarily the most abundant because their reduced statistical weights may make them less probable. Instead, for TRAP species with 4 to 9 Trp per TRAP, the second most energetically favorable configurations are most abundant, due to their consistently greater statistical weights (Eq. 9).
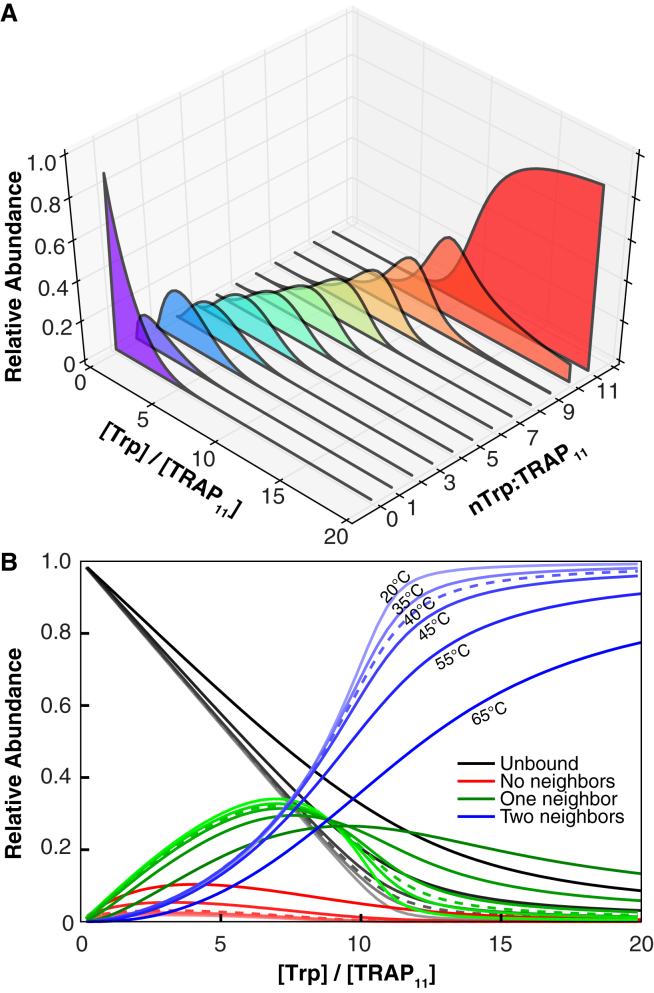
Figure 5.
Populations of Trp+TRAP species during the ITC titration predicted by the nonadditive model using the best-fit parameters from Table 1. (A) The relative abundance at each titration point, of TRAP11 species with 0–11 bound Trp, colored purple to red for the ITC titration experiment performed at 40°C (starting TRAP11 concentration = 6.81 μM). (B) The relative abundance of empty sites (black), occupied sites with no bound neighbors (red), occupied sites with one bound neighbor (green), and occupied sites with two bound neighbors (blue), as a function of Trp/TRAP ratio during ITC titrations over a range of temperatures. To see this figure in color, go online.
Examining whether individual bound sites have bound neighbors (Fig. 5 B) reveals that occupied sites without any bound neighbors never exceed >10% of all sites. This supports the intuition that cooperativity favors clusters of pairs of occupied sites (Fig. S11). This may have important functional implications: if TRAP binds its cognate mRNAs by an initial weak encounter with a single GAG repeat to an activated pair of protomers, followed by a rapid binding of additional tandem GAG repeats to adjacent activated TRAP protomers, the clustering of activated TRAP subunits may permit high-affinity RNA binding by incompletely saturated TRAP oligomers. Indeed, five sequential GAG triplets bound to activated TRAP subunits are sufficient for low nanomolar binding affinities (51). This may also explain observations that relatively small amounts of wild-type TRAP subunits in a context of inactivatable mutant protomers nevertheless enable robust RNA binding (52).
Comparison to Hill analysis
From the population trajectories computed from the partition function of model NN-na, we simulated Hill analysis to provide a qualitative comparison of the two approaches. Hill analysis is typically performed by precomputing a fractional saturation Θ from some experimental observable, then fitting either Θ versus [L] (free ligand concentration), or log [Θ/(1 − Θ)] versus log [L] to either nonlinear or linearized forms of the Hill equation. Saturation plots of predicted site occupancy at each temperature across the experimental concentrations of free ligand illustrate the difficulty of quantifying cooperative behavior via traditional Hill analysis, even with unrealistically low experimental uncertainties of 1% (Fig. S13). Fitting the population trajectories using the Hill expression yielded a temperature-dependent apparent KD ranging from of 0.1 μM at 20°C to 10 μM at 55°C, and weakly positive Hill coefficients ranging from 1.4 to 1.6 over the same temperature range (Fig. S14). These values, reflecting slight-to-modest cooperativity, are generally consistent with the results of previous attempts to quantify cooperativity in TRAP, while also being devoid of mechanistic insight.
Structural insights
Heat capacity changes ΔCp associated with Trp binding provide a means to quantify changes in accessible protein-solvent conformational states (18, 19, 47, 53, 54), and have the potential to provide rich insights into structure-thermodynamic relationships. Best fit parameters for model NN-na (Tables 1 and S2; Fig. S5) indicate that binding of Trp to a site with empty neighbors is associated with a negligible ΔCp,0, while structure-based surface area calculations suggested an expected ΔCp of −0.088 kcal mol−1 K−1 for burial of a Trp within its binding site on TRAP (27). Trp binding to sites with one or two occupied neighbors is associated with large negative ΔCp,oe, ΔCp,oo values of −0.49, and −0.46 kcal mol−1 K−1. These are comparable to the value of −0.37 kcal mol−1 K−1 obtained for Trp binding to wild-type TRAP, the excess of which might be explained by binding-coupled folding of ∼19 residues. Because the burial of nonpolar residues and binding-linked structural changes both contribute to a negative ΔCp, these findings suggest that binding to sites with no occupied neighbors does not result in significant structural rearrangement, while the small negative ΔCp from solvent release is offset by additional roughness in the protein-solvent free energy landscape. However, the large ΔCp,oe and ΔCp,oe do reflect structural rearrangement and reduction in the number of thermally accessible protein-solvent states.
Conclusions
These observations allow us to propose a mechanism for cooperative Trp binding to TRAP. Initial weak binding by some Trp molecules to isolated sites provides a metastable platform for opportunistic binding by additional Trp, upon which the protein-ligand-solvent system becomes more ordered and compact, adopting a hololike state. Once two-to-three pairs of NN interactions are formed (i.e., four-to-six bound Trp), there is little additional change in the protein structure upon additional Trp binding. This microscopically informed result is consistent with a phenomenological kinetic analysis of Trp binding to A28I TRAP through stopped-flow fluorescence that was best fit by a two-step pathway, in which an initial Trp binding step with a fast release rate enables a second, high-affinity Trp binding mode characterized by a greatly retarded Trp release rate (28). While direct application of a mechanistically informed NN model to analysis of the kinetic data are beyond the scope of this work, the results presented here provide compelling microscopic detail to explain that phenomenological observation.
Oligomeric proteins are prevalent across biology (55, 56, 57), and their overrepresentation in regulatory systems (58, 59) highlights the importance of an inter-subunit communication fine-tuning function. Compared to hemoglobin, which is the best studied model of cooperativity, the tryptophan binding behavior of TRAP presents several unique challenges, including the large number of ligand binding sites. Unlike the 16 possible and until very recently experimentally indistinguishable configurations of hemoglobin (60), the >100 potentially energetically distinct states of TRAP provide a daunting conceptual and logistical conundrum.
Commonly used phenomenological models represent a fundamentally unrealistic oversimplification of a binding mechanism, and thus are limited in the amount of information that can be extracted from binding data. Here, we explored application of mechanistically informed statistical thermodynamic models, and global analysis, to obtain microscopic thermodynamic parameters from bulk thermodynamic experiments. In the case of Bst A28I TRAP, our data quantify the energetic coupling between sites and indicate that site-site communication between the sites is not simply additive, such that having one neighboring Trp induces almost as much structuring as having two neighboring Trp. These findings advance our understanding of the TRAP biosensor and provide insights into the microscopic origins of cooperativity. Although unique to bacilli, TRAP represents a common and important class of allosteric proteins both in its quaternary structure and dynamic behavior; we expect the approach outlined here to be generally applicable to, and informative for, other multimeric allosteric systems.
The approach outlined here provides deeper insight into Trp-TRAP interactions and argues for broader use of mechanistically informed models when fitting and interpreting thermodynamic binding data (20, 61). The Hill equation and Hill coefficient remain in common use in the biochemistry literature, in large part because it is generally easy to measure, and provides some qualitative metric for comparison. However, its limited mechanistic value should discourage quantitative use and interpretation (7, 8). In contrast, the tools of structural biology, statistical thermodynamics, and mathematical modeling of mechanisms have the potential to take us beyond phenomenological treatments of allostery to an understanding of its microscopic origins and mechanisms (4, 62, 63, 64).
Author Contributions
E.C.I., I.R.K., P.G., and M.P.F. designed and performed the research, and analyzed data; and E.C.I., I.R.K., and M.P.F. wrote the article.
Acknowledgments
The authors thank Philip Maini (Oxford), whose discussions regarding homotropic allostery inspired parts of this work, and James Cole (University of Connecticut), Carlos Amero, Joseph Sachleben, Craig McElroy, Vicki Wysocki and Melody Holmquist (OSU) for helpful discussion.
This work was supported by National Institutes of Health (NIH) grant No. GM077234 (to M.P.F. and P.G.), National Science Foundation (NSF) MCB grant No. 1019960 (to P.G.), and in part by an allocation of computing time from the Ohio Supercomputer Center.
Editor: David Eliezer.
Footnotes
Fourteen figures and two tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30245-X.
Supporting Material
References
- 1.Changeux J.P. 50th anniversary of the word “allosteric”. Protein Sci. 2011;20:1119–1124. doi: 10.1002/pro.658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Swain J.F., Gierasch L.M. The changing landscape of protein allostery. Curr. Opin. Struct. Biol. 2006;16:102–108. doi: 10.1016/j.sbi.2006.01.003. [DOI] [PubMed] [Google Scholar]
- 3.Cui Q., Karplus M. Allostery and cooperativity revisited. Protein Sci. 2008;17:1295–1307. doi: 10.1110/ps.03259908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hilser V.J., Wrabl J.O., Motlagh H.N. Structural and energetic basis of allostery. Annu. Rev. Biophys. 2012;41:585–609. doi: 10.1146/annurev-biophys-050511-102319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cantor C.R., Schimmel Paul R. W. H. Freeman; San Francisco, CA: 1980. Biophysical Chemistry Part III: The Behavior of Biological Macromolecules. [Google Scholar]
- 6.Fersht A. W. H. Freeman; New York: 1999. Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding. [Google Scholar]
- 7.Weiss J.N. The Hill equation revisited: uses and misuses. FASEB J. 1997;11:835–841. [PubMed] [Google Scholar]
- 8.Holt J.M., Ackers G.K. The Hill coefficient: inadequate resolution of cooperativity in human hemoglobin. Methods Enzymol. 2009;455:193–212. doi: 10.1016/S0076-6879(08)04207-9. [DOI] [PubMed] [Google Scholar]
- 9.Monod J., Wyman J., Changeux J.-P. On the nature of allosteric transitions: a plausible model. J. Mol. Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 10.Koshland D.E.J., Jr., Némethy G., Filmer D. Comparison of experimental binding data and theoretical models in proteins containing subunits. Biochemistry. 1966;5:365–385. doi: 10.1021/bi00865a047. [DOI] [PubMed] [Google Scholar]
- 11.Eaton W.A., Henry E.R., Mozzarelli A. Is cooperative oxygen binding by hemoglobin really understood? Nat. Struct. Biol. 1999;6:351–358. doi: 10.1038/7586. [DOI] [PubMed] [Google Scholar]
- 12.Zhao H., Piszczek G., Schuck P. SEDPHAT—a platform for global ITC analysis and global multi-method analysis of molecular interactions. Methods. 2015;76:137–148. doi: 10.1016/j.ymeth.2014.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Freiburger L., Auclair K., Mittermaier A. Global ITC fitting methods in studies of protein allostery. Methods. 2015;76:149–161. doi: 10.1016/j.ymeth.2014.12.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Le V.H., Buscaglia R., Lewis E.A. Modeling complex equilibria in isothermal titration calorimetry experiments: thermodynamic parameters estimation for a three-binding-site model. Anal. Biochem. 2013;434:233–241. doi: 10.1016/j.ab.2012.11.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jelesarov I., Bosshard H.R. Isothermal titration calorimetry and differential scanning calorimetry as complementary tools to investigate the energetics of biomolecular recognition. J. Mol. Recognit. 1999;12:3–18. doi: 10.1002/(SICI)1099-1352(199901/02)12:1<3::AID-JMR441>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- 16.Privalov G.P., Privalov P.L. Problems and prospects in microcalorimetry of biological macromolecules. Methods Enzymol. 2000;323:31–62. doi: 10.1016/s0076-6879(00)23360-0. [DOI] [PubMed] [Google Scholar]
- 17.Makhatadze G.I., Privalov P.L. Energetics of protein structure. Adv. Protein Chem. 1995;47:307–425. doi: 10.1016/s0065-3233(08)60548-3. [DOI] [PubMed] [Google Scholar]
- 18.Prabhu N.V., Sharp K.A. Heat capacity in proteins. Annu. Rev. Phys. Chem. 2005;56:521–548. doi: 10.1146/annurev.physchem.56.092503.141202. [DOI] [PubMed] [Google Scholar]
- 19.Sturtevant J.M. Heat capacity and entropy changes in processes involving proteins. Proc. Natl. Acad. Sci. USA. 1977;74:2236–2240. doi: 10.1073/pnas.74.6.2236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Freire E., Schön A., Velazquez-Campoy A. Isothermal titration calorimetry: general formalism using binding polynomials. Methods Enzymol. 2009;455:127–155. doi: 10.1016/S0076-6879(08)04205-5. [DOI] [PubMed] [Google Scholar]
- 21.Brown A. Analysis of cooperativity by isothermal titration calorimetry. Int. J. Mol. Sci. 2009;10:3457–3477. doi: 10.3390/ijms10083457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gollnick P., Babitzke P., Yanofsky C. Complexity in regulation of tryptophan biosynthesis in Bacillus subtilis. Annu. Rev. Genet. 2005;39:47–68. doi: 10.1146/annurev.genet.39.073003.093745. [DOI] [PubMed] [Google Scholar]
- 23.McElroy C., Manfredo A., Foster M. TROSY-NMR studies of the 91-kDa TRAP protein reveal allosteric control of a gene regulatory protein by ligand-altered flexibility. J. Mol. Biol. 2002;323:463–473. doi: 10.1016/s0022-2836(02)00940-3. [DOI] [PubMed] [Google Scholar]
- 24.Malay A.D., Watanabe M., Tame J.R.H. Crystal structure of unliganded TRAP: implications for dynamic allostery. Biochem. J. 2011;434:427–434. doi: 10.1042/BJ20101813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kleckner I.R., Gollnick P., Foster M.P. Mechanisms of allosteric gene regulation by NMR quantification of microsecond-millisecond protein dynamics. J. Mol. Biol. 2012;415:372–381. doi: 10.1016/j.jmb.2011.11.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Antson A.A., Otridge J., Gollnick P. The structure of trp RNA-binding attenuation protein. Nature. 1995;374:693–700. doi: 10.1038/374693a0. [DOI] [PubMed] [Google Scholar]
- 27.McElroy C.A., Manfredo A., Foster M.P. Thermodynamics of tryptophan-mediated activation of the trp RNA-binding attenuation protein. Biochemistry. 2006;45:7844–7853. doi: 10.1021/bi0526074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kleckner I.R., McElroy C.A., Foster M.P. Homotropic cooperativity from the activation pathway of the allosteric ligand-responsive regulatory trp RNA-binding attenuation protein. Biochemistry. 2013;52:8855–8865. doi: 10.1021/bi401364v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tellinghuisen J. A study of statistical error in isothermal titration calorimetry. Anal. Biochem. 2003;321:79–88. doi: 10.1016/s0003-2697(03)00406-8. [DOI] [PubMed] [Google Scholar]
- 30.Cantor C., Schimmel P. W. H. Freeman; San Francisco, CA: 1980. Biophysical Chemistry. [Google Scholar]
- 31.Vega S., Abian O., Velazquez-Campoy A. A unified framework based on the binding polynomial for characterizing biological systems by isothermal titration calorimetry. Methods. 2015;76:99–115. doi: 10.1016/j.ymeth.2014.09.010. [DOI] [PubMed] [Google Scholar]
- 32.Brush S.G. History of the Lenz-Ising model. Rev. Mod. Phys. 1967;39:883–893. [Google Scholar]
- 33.Saroff H.A., Kiefer J.E. Analysis of the binding of ligands to large numbers of sites: the binding of tryptophan to the 11 sites of the trp RNA-binding attenuation protein. Anal. Biochem. 1997;247:138–142. doi: 10.1006/abio.1997.2039. [DOI] [PubMed] [Google Scholar]
- 34.Gasteiger E., Hoogland C., Bairoch A. The Proteomics Protocols Handbook. Humana Press; New York: 2005. Protein identification and analysis tools on the ExPASy server; pp. 571–607. [Google Scholar]
- 35.MicroCal . Malvern Instruments; Malvern, UK: 2010. ITC Data Analysis in Origin. [Google Scholar]
- 36.Brent R.P. An algorithm with guaranteed convergence for finding a zero of a function. Comput. J. 1971;14:422–425. [Google Scholar]
- 37.Oliphant T.E. SciPy: open source scientific tools for Python. Comput. Sci. Eng. 2007;9:10–20. [Google Scholar]
- 38.Efron B., Tibshirani R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat. Sci. 1986;1:54–75. [Google Scholar]
- 39.Press W.H., Teukolsky S.A., Flannery B.P. 2nd Ed. Cambridge University Press; Cambridge, UK: 1992. Numerical Recipes in C: The Art of Scientific Computing. [Google Scholar]
- 40.Andrae, R., T. Schulze-Hartung, and P. Melchior. 2010. Dos and don’ts of reduced χ2. arXiv Prepr. arXiv1012.3754. 1–12.
- 41.Fletcher R., Powell M. A rapidly convergent descent method for minimization. Comput. J. 1963;6:163–168. [Google Scholar]
- 42.Williams, T., and C. Kelley. 2010. Gnuplot 4.4: an interactive plotting program. Available at http://sourceforge. net/projects/gnuplot.
- 43.Hunter J.D. Matplotlib: a 2D graphics environment. Comput. Sci. Eng. 2007;9:90–95. [Google Scholar]
- 44.Heddle J.G., Okajima T., Tame J.R.H. Dynamic allostery in the ring protein TRAP. J. Mol. Biol. 2007;371:154–167. doi: 10.1016/j.jmb.2007.05.013. [DOI] [PubMed] [Google Scholar]
- 45.Velazquez-Campoy A., Freire E. Isothermal titration calorimetry to determine association constants for high-affinity ligands. Nat. Protoc. 2006;1:186–191. doi: 10.1038/nprot.2006.28. [DOI] [PubMed] [Google Scholar]
- 46.Freiburger L.A., Auclair K., Mittermaier A.K. Elucidating protein binding mechanisms by variable-c ITC. ChemBioChem. 2009;10:2871–2873. doi: 10.1002/cbic.200900614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Winzor D.J., Jackson C.M. Interpretation of the temperature dependence of equilibrium and rate constants. J. Mol. Recognit. 2006;19:389–407. doi: 10.1002/jmr.799. [DOI] [PubMed] [Google Scholar]
- 48.Beechem J.M. Global analysis of biochemical and biophysical data. Methods Enzymol. 1992;210:37–54. doi: 10.1016/0076-6879(92)10004-w. [DOI] [PubMed] [Google Scholar]
- 49.Jaqaman K., Danuser G. Linking data to models: data regression. Nat. Rev. Mol. Cell Biol. 2006;7:813–819. doi: 10.1038/nrm2030. [DOI] [PubMed] [Google Scholar]
- 50.Motulsky H., Christopoulos A. Oxford University Press; Oxford, UK: 2004. Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting. [Google Scholar]
- 51.Elliott M.B., Gottlieb P.A., Gollnick P. The mechanism of RNA binding to TRAP: initiation and cooperative interactions. RNA. 2001;7:85–93. doi: 10.1017/s135583820100173x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Li P.T.X., Scott D.J., Gollnick P. Creating hetero-11-mers composed of wild-type and mutant subunits to study RNA binding to TRAP. J. Biol. Chem. 2002;277:11838–11844. doi: 10.1074/jbc.M110860200. [DOI] [PubMed] [Google Scholar]
- 53.Spolar R., Record M. Coupling of local folding to site-specific binding of proteins to DNA. Science. 1994;263:777–784. doi: 10.1126/science.8303294. [DOI] [PubMed] [Google Scholar]
- 54.Murphy K., Privalov P., Gill S. Common features of protein unfolding and dissolution of hydrophobic compounds. Science. 1990;247:559–561. doi: 10.1126/science.2300815. [DOI] [PubMed] [Google Scholar]
- 55.Ali M.H., Imperiali B. Protein oligomerization: how and why. Bioorg. Med. Chem. 2005;13:5013–5020. doi: 10.1016/j.bmc.2005.05.037. [DOI] [PubMed] [Google Scholar]
- 56.Dayhoff J.E., Shoemaker B.A., Panchenko A.R. Evolution of protein binding modes in homooligomers. J. Mol. Biol. 2010;395:860–870. doi: 10.1016/j.jmb.2009.10.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kuriyan J., Eisenberg D. The origin of protein interactions and allostery in colocalization. Nature. 2007;450:983–990. doi: 10.1038/nature06524. [DOI] [PubMed] [Google Scholar]
- 58.Goodsell D.S., Olson A.J. Structural symmetry and protein function. Annu. Rev. Biophys. Biomol. Struct. 2000;29:105–153. doi: 10.1146/annurev.biophys.29.1.105. [DOI] [PubMed] [Google Scholar]
- 59.Hashimoto K., Nishi H., Panchenko A.R. Caught in self-interaction: evolutionary and functional mechanisms of protein homooligomerization. Phys. Biol. 2011;8:035007. doi: 10.1088/1478-3975/8/3/035007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Viappiani C., Abbruzzetti S., Eaton W.A. Experimental basis for a new allosteric model for multisubunit proteins. Proc. Natl. Acad. Sci. USA. 2014;111:12758–12763. doi: 10.1073/pnas.1413566111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Velazquez-Campoy A., Goñi G., Medina M. Exact analysis of heterotropic interactions in proteins: characterization of cooperative ligand binding by isothermal titration calorimetry. Biophys. J. 2006;91:1887–1904. doi: 10.1529/biophysj.106.086561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Tsai C.-J., Nussinov R. A unified view of “how allostery works”. PLOS Comput. Biol. 2014;10:e1003394. doi: 10.1371/journal.pcbi.1003394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Motlagh H.N., Wrabl J.O., Hilser V.J. The ensemble nature of allostery. Nature. 2014;508:331–339. doi: 10.1038/nature13001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Boehr D.D., Nussinov R., Wright P.E. The role of dynamic conformational ensembles in biomolecular recognition. Nat. Chem. Biol. 2009;5:789–796. doi: 10.1038/nchembio.232. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.