Mechanistic Models Fit to Variable Temperature Calorimetric Data Provide Insights into Cooperativity

Abstract

Allostery pervades macromolecular function and drives cooperative binding of ligands to macromolecules. To decipher the mechanisms of cooperative ligand binding it is necessary to define at a microscopic level the structural and thermodynamic consequences of binding of each ligand to its allosterically coupled site(s). However, dynamic sampling of alternative conformations (microstates) in allosteric molecules complicates interpretation of both structural and thermodynamic data. Isothermal titration calorimetry has the potential to directly quantify the thermodynamics of allosteric interactions, but usually falls short of enabling mechanistic insight. This is because 1) its measurements reflect the sum of overlapping caloric processes involving binding-linked population shifts within and between microstates, and 2) data are generally fit with phenomenological binding polynomials that are underdetermined. Nevertheless, temperature-dependent binding data have the potential to resolve overlapping thermodynamic processes, while mechanistically constrained models enable hypothesis testing and identification of informative parameters. We globally fit temperature-dependent isothermal titration calorimetry data for binding of 11 tryptophan ligands to the homo-undecameric trp RNA-binding Attenuation Protein from Bacillus stearothermophilus using nearest-neighbor statistical thermodynamic models. This approach allowed us to distinguish alternative nearest-neighbor interaction models, and quantifies the thermodynamic contribution of neighboring ligands to individual binding sites. We also perform conventional Hill equation modeling and illustrate how comparatively limited it is in quantitative or mechanistic value. This work illustrates the potential of mechanistically constrained global fitting of binding data to yield the microscopic thermodynamic parameters essential for deciphering mechanisms of cooperativity in a wide range of ligand-regulated homo-oligomeric assemblies.

Introduction

Allostery is ubiquitous in regulated cellular processes and is an important consideration in the design of artificial ligands for therapeutics, or for engineering novel functions (1, 2, 3, 4). Its hallmark is the observation that ligand binding is altered by binding of one or more additional ligands at distant sites in the same target. In the case of homotropic allostery, i.e., when the ligands are the same, it is commonly diagnosed from binding curves that are fit poorly by a standard Langmuir isotherm (5, 6). Although such curves (sigmoidal, in the case of positive cooperativity) can be diagnostic, the common practice of fitting such data with the Hill equation provides an unintuitive coefficient with limited to no mechanistic value (7, 8). The next level of sophistication in modeling binding data is to define a binding polynomial that assigns a distinct set of thermodynamic parameters for each discernable ligand binding event. The venerable “concerted” MWC and “sequential” KNF models (9, 10) are two such formalisms that can successfully predict cooperative behavior in many allosteric systems. While more informative than Hill equation modeling, the resulting set of thermodynamic constants imperfectly captures the mechanism and magnitude of allosteric communication (4, 11). On the other hand, if a specific mechanistic binding model is known or can be appropriately posed, fitting the data with polynomials derived from such mechanisms has the potential to provide the level of precision required to understand allosteric communication at the microscopic level.

Isothermal titration calorimetry (ITC) has emerged as the premier technique for probing the thermodynamics of bimolecular interactions, both independently and when combined with complementary methods (12, 13, 14). ITC directly measures the enthalpy change (ΔH) resulting from binding of a ligand to a macromolecule; fitting the data with an appropriate binding model yields the overall free energy change ΔG via the equilibrium association constant K_A (15, 16). In addition, the temperature dependence of ΔH yields the change in heat capacity (ΔC_p), which is typically dominated by changes in the system’s hydration state, but also reflects macromolecular degrees of freedom, and thus can provide information about structural perturbations (17, 18, 19). Cooperativity affects each of these measurable values, because binding of successive ligands to a macromolecule with multiple binding sites may occur with higher or lower affinity, be more or less enthalpic, and be associated with different degrees of structural remodeling (13, 20, 21). Despite its strengths, ITC analyses often fall short of providing mechanistic detail, in part because its bulk thermodynamic measurements reflect the sum of simultaneous binding-coupled caloric processes that arise from population shifts between the microstates of the system, and because thermograms are generally fit with phenomenological multiparameter binding polynomials that are underdetermined (12, 13, 20, 21). Indeed, because the thermograms are affected by both ΔH and K_A, positive and negative cooperativity can yield strikingly similar thermograms (e.g., Fig. S1 in the Supporting Material).

As a paradigmatic model of homotropic and heterotropic allostery, cooperativity in the ring-shaped homo-undecameric (11-mer) trp RNA-binding Attenuation Protein (TRAP) (Fig. 1 A) has been a matter of interest since the discovery of its function and quaternary structure (22). In many species of bacilli, TRAP regulates expression of the trp operon through RNA binding activity that is allosterically regulated by binding L-tryptophan (Trp) to its 11 structurally identical sites located at its subunit interfaces (Fig. 1 B). Nuclear magnetic resonance (NMR), proteolytic, and crystallographic data (23, 24) indicate that in its Trp-free “apo” state loops in TRAP that shield its binding sites from bulk solvent are dynamic and structurally heterogeneous. This disorder has been proposed to simultaneously mask its RNA binding surface, and to allow gated access by Trp, whereas the loops rigidify upon Trp binding, stabilizing the architecture of the RNA binding surface of TRAP (23, 25). By virtue of the binding-coupled structural changes and close proximity of adjacent Trp binding sites (separated by one β-strand), cooperativity in Trp binding to TRAP is expected, although thermodynamic and kinetic measurements to date have yielded seemingly contradictory conclusions regarding its presence, magnitude, or sign (i.e., cooperative, noncooperative, or anticooperative) (24, 25, 26, 27, 28).

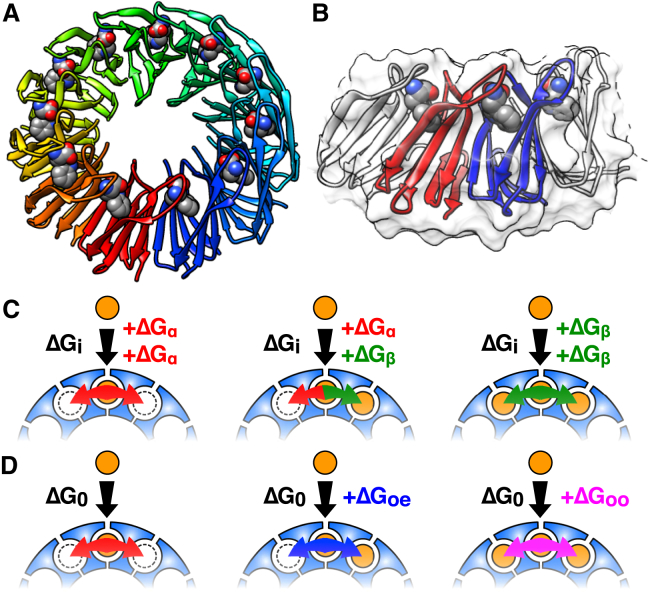
Figure 1.

TRAP is a biosensor with 11 equivalent binding sites for tryptophan. (A) Crystal structure of Trp-bound TRAP₁₁ (26); bound Trp are shown as spheres. (B) Closeup of two neighboring protomers in the crystal structure (red and blue) showing proximity of bound tryptophan molecules. (C) NN-a model of cooperativity between sites, in which binding free energy is the sum of an intrinsic free energy ΔG_i plus coupling to either empty (ΔG_α) or occupied (ΔG_β) neighboring sites. (D) NN-na model, in which binding to a site flanked by two empty sites has a reference ΔG₀, modified by coupling free energies when the site is flanked by one or two occupied neighbors (ΔG_oe, ΔG_oo), respectively. To see this figure in color, go online.

To obtain mechanistically informative parameters, ITC thermograms should be fit with a binding polynomial equation representing a suitable binding model. In the case of TRAP, with 11 potential binding sites for Trp, each of which could either be empty or occupied, there exist 2¹¹ = 2048 possible Trp-TRAP configurations. The 11-fold symmetry of the TRAP₁₁ rings result in structural and therefore thermodynamic degeneracy (e.g., the 11 configurations with one bound Trp are structurally identical), leaving 125 unique Trp-TRAP configurations. If each of these configurations were to have unique thermodynamic profiles (i.e., their own ΔH, K_A), quantifying them by fitting the ITC thermograms to such a multiparameter phenomenological binding polynomial would certainly not yield meaningful values, despite the often-oversampled nature of ITC data (29).

A reduction in the number of parameters in a complex binding polynomial can be achieved by applying a model that mechanistically relates the energetics of the system from the first ligand binding event to the last (30, 31). Such a model based on Ising lattices (32) was previously proposed by Saroff and Kiefer (33) to describe Trp-TRAP equilibrium dialysis data by posing that the binding affinity of a given site is modulated by additive contributions from the closest neighboring sites; i.e., those to the left and right flanking sites in the TRAP ring (Fig. 1 B). Although in that instance a single set of binding data was apparently insufficient for convergence to a unique set of parameters, such an approach is also compelling because it provides a clear mechanistic basis for quantifying the energetic interactions between sites.

To quantify cooperativity in Trp binding to TRAP, we recorded ITC data over a range of temperatures (which alter the thermograms through its effect on ΔH and K_A), and the resulting data were globally fit using binding polynomials derived from: 1) a minimal phenomenological model, 2) a partition function arising from the additive Saroff and Kiefer (33) nearest-neighbor (NN) statistical thermodynamic model, or 3) a partition function from a nonadditive variant of this NN model. Our findings reveal unique heat capacity changes ΔC_p for each binding mode, allowing us to deconvolute ΔH and ΔG values for overlapping binding events, thereby distinguishing the two alternative NN models of cooperativity. With the partition function thus defined and parameterized, it is possible to itemize the populations and energies of all states of the system at arbitrary concentrations and temperatures, thus illuminating the Trp-TRAP activation pathway. When paired with structural information, the resulting microscopic thermodynamic values constitute a quantitative basis for a detailed understanding of the mechanism of allostery.

Materials and Methods

Mutagenesis, expression, and purification of Bacillus stearothermophilus A28I TRAP was performed as described in McElroy et al. (23) and Kleckner et al. (25). HPLC-purified and refolded Trp-free (apo) TRAP was dialyzed against sodium phosphate binding buffer: 100 mM NaCl, 50 mM NaPO₄, pH 8.0 at 25°C, 0.02% NaN₃. The resulting solution was 6.818 ≥ 0.181 μM TRAP₁₁ (75 ± 2 μM binding sites), with concentration measured using UV absorbance at 280 nm with ε = 2980 M⁻¹ cm⁻¹, calculated using the tool ProtParam (34). Trp solutions were prepared by adding solid L-tryptophan (USB Corporation, Cleveland, OH) to buffer matched to the TRAP stock via dialysis, to concentrations of 610 or 765 μM based on a starting stock of 2030 ± 43 μM quantified by UV absorbance at 278 nm with extinction coefficient ε = 5579 M⁻¹ cm⁻¹ (27). Because accurate concentrations are essential for analysis, all samples were prepared from their respective stock with dilution factors measured using an analytical balance precise to 100 μg.

All isotherms were recorded on a MicroCal VP-ITC (Malvern Instruments, Malvern, Worcestershire, UK). Experiments acquired at 20, 35, 40, and 45°C were performed by an initial 3 μL injection followed by 56 × 5 μL injections of 610 μM Trp into 75 μM TRAP. Isotherms at 55 and 65°C were performed using 95 × 3 μL injections of 765 μM Trp into 75 μM TRAP. A reference power of 30 μcal/s and a stirring speed of 300 rpm were used throughout. The reference cell solution was deionized water. The resulting raw differential isotherms were baseline-corrected and integrated using the default ORIGIN routines provided by the manufacturer (35). For both sets of titrations, the first injection point was not fitted.

We implemented a custom ITC data fitting library, “itcsimlib”, to numerically optimize the desired parameters of the various binding models, which were compiled separately as shared libraries. At each step during parameter optimization for the additive and nonadditive statistical thermodynamics models, the predicted free energies and enthalpies were calculated for each of the 2048 (2¹¹) TRAP+nTrp configurations. Because each site of TRAP can exist in either a Trp-bound or unbound state, the 2048 possible configurations can be represented by the 11-digit binary representation of the configuration’s index number, such as 00000000000 for the reference state of apo TRAP at index 0, 11111111111 for index 2047 of holo TRAP, 01111100100 for configuration index 996 containing six bound tryptophans, etc. For each configuration index i, its characteristic aggregate ΔG_i will be the sum of the individual microscopic binding site free energies ΔG_j of the 11 active sites in that configuration:

$$\Delta G_i=\sum _j^{11}\Delta G_j,$$ (1)

where ΔG_j depends upon the specific model and the occupancy state of the neighboring (j+1 or j−1) sites. In all cases, the configuration is treated as a circular array. ΔH_i is obtained in the same fashion as ΔG_i, except by summing the characteristic enthalpies ΔH_j.

The absolute probability (P_i) of each configuration at a given concentration of free Trp ligand [L] can be obtained from the relative probabilities R_i, which themselves are obtained from the configuration’s ΔG_i and the Boltzmann distribution:

$$\begin{array}{c}{R}_i=e^{\Delta G_i/RT}\left[L\right]\\ P_i=\frac{R_i}{\Xi }\\ =\frac{R_i}{\sum R_{1-2048}},\end{array}$$ (2)

where n_i is the number of Trp bound to that configuration.

At each of the ITC titration points, the free ligand concentration [L] is not a priori known, but is obtained from the mass balance equation by minimizing the discrepancy between the known total Trp concentration L_t at each titration point and the predicted total ligand concentration, which consists of the free Trp and bound to TRAP, where M_t is the total concentration of the TRAP oligomer macromolecule:

$$\Delta L_t=L_t-\left[L\right]-M_t\sum _i^{2048}{n}_i{P}_i.$$ (3)

This is achieved in itcsimlib by iterative, numerical minimization of ΔL_t by optimization of [L] using the GNU scientific library’s implementation of Brent’s method (36, 37), with [L] = L_t and [L] = 0 as initial bracketing guesses. When this method has converged to a ΔL_t of <1 nM, the final probabilities are retained for the evaluation of total enthalpy. Determination of the total heat Q present in the system at injection k can then be obtained at each titration point:

$$Q_k=\frac{V_0{M}_t}{\Delta V_k{L}_0}\sum _i^{2048}\Delta H_i{P}_i,$$ (4)

where V₀ is the working volume of the ITC cell and ΔH_i has been previously calculated for each configuration as described. The heat is normalized by the amount of ligand injected (ΔV_kL₀).

Analysis requires correction for the volume injected from the titration syringe, which both dilutes the existing solution and displaces an equal volume into the cell stem. Because stirring is continuous during each injection, solution displaced into the cell stem no longer comprises the working volume and only partially contributes to the heat sensed by the instrument (35). Therefore, both the actual and effective dilution of the components must be considered to avoid systematic overestimation of the heat evolved or consumed by the system. Although there are several methods in the literature for calculating this dilution (20, 21), the method recommended by the manufacturer of the VP-ITC instrument is used in itcsimlib (35):

$$\begin{array}{c}\Delta V_k=\sum _0^k{V}_k,\\ M_{t,k}=M_t^0\left(\frac{1-\Delta V_k/2V_0}{1+\Delta V_k/2V_0}\right),\\ L_{t,k}=L_t^0\left(\frac{1}{1+\Delta V_k/2V_0}\right),\end{array}$$ (5)

where k is the number of the current injection and L_t⁰ is the hypothetical concentration of ligand, assuming that all of the injected ligand remains in the cell. ΔV_k is the total change in volume as it is the sum of the injected volumes up to V_k, and V₀ is the actual working volume of the cell (1.4166 mL for the VP-ITC).

During the ITC experiment, the change in enthalpy of the system is measured at each titration point, and the aforementioned effect of displacement from the working volume must be taken into account. Using the method described above, the displaced material contributes ∼50% as much heat as the equivalent material in the working volume (35):

$$\Delta Q_k=Q_k+\frac{V_k}{V_0}\left(\frac{Q_k+Q_{k-1}}{2}\right)-Q_{k-1},$$ (6)

where Q_k is the total calculated heat at the current injection, and Q_k−1 is the calculated heat at the previous injection. The resulting ΔQ_k can be directly compared to the integrated measurements of differential heat obtained from the instrument through a χ² goodness-of-fit metric for each experiment:

$${\chi }^2=\frac{1}{n}\sum _k^n\frac{{\left(\Delta Q_{\text{exp},k}-\Delta Q_{\text{fit},k}\right)}^2}{{\sigma }^2}.$$ (7)

Because uncertainties in the calculated heat can be distorted by the normalization to injected ligand concentration as well as errors in baseline determination, the uncertainty σ² for each experiment was estimated in itcsimlib by fitting a first-order Savitsky-Golay smoothing spline with a seven-point window to the experimental ΔQ values and calculating the standard deviation of the values from the spline. Confidence limits in optimized model parameters were estimated using two methods: Bootstrapped uncertainties were generated by refitting 200 synthetic datasets composed of the original fit to which randomly selected residuals were “added” with the original parameters to which a 10% variance was applied (38). Chi-square boundary uncertainties were obtained by incrementing an individual parameter above and below its best-fit value while optimizing the remaining model parameters until the resulting goodness-of-fit χ² exceeded the best-fit χ² plus the expected variance for the fitted data points (39, 40).

Numerical optimization used the Powell algorithm (41) exclusively, although other optimization algorithms were also evaluated in itcsimlib. For the initial grid fits used to reduce parameter space, the starting values for parameters not explicitly restrained by the grid were initially set to those obtained from a global fit using a phenomenological one-mode model. Figures are generated using gnuplot (42) and matplotlib (43) routines implemented in itcsimlib.

Results and Discussion

Substoichiometric binding conditions are important for discerning allostery

Previously, we performed ITC experiments of Trp binding to wild-type TRAP from the thermophile B. stearothermophilus (Bst) and found the data fit well to a single-site binding model, implying no homotropic cooperativity (27), a finding at odds with results obtained with the mesophile B. subtilis (Bsu) TRAP (44), as well as intuition based on the structure of TRAP (Fig. 1) (26) and the role of coupled folding in its activation (25). However, those ITC experiments were not designed to assess cooperativity; instead they were designed to accurately measure the net ΔC_p to quantify the degree of folding resulting from Trp binding (27). By performing the ITC experiments at higher c values (c = [TRAP]_Total/K_d), uncertainty in measured ΔH is minimized, but the existence of different binding modes may be missed (15, 45, 46) (Fig. S2). Using lower c values, we observed that ITC titrations of wild-type TRAP do exhibit multiple binding modes, as do titrations with Bsu TRAP (44) (Fig. S3). For these experiments, we utilize the Bst TRAP mutant A28I to enable direct comparison to existing kinetic and NMR data (23, 25). This mutation introduces an additional NMR probe in one of the gating loops above the Trp binding site, and is fully functional in Trp and RNA binding (25, 27, 28).

NN models of Trp-TRAP

Considering that Trp binding to sites on distant parts of the TRAP ring (i.e., farther than one binding site, or ∼25 Å; Fig. 1 A) are less likely to be thermodynamically coupled than the adjacent sites, a nearest-neighbor (NN) model makes the simplifying assumption that interactions between neighboring sites dominate binding thermodynamics (33). Importantly, an NN model reduces the number of potentially energetically distinct binding modes, and allows them to be described by combinations of just a few microscopic thermodynamic parameters.

To automate bookkeeping when generating partition functions encompassing the 2048 (2¹¹) possible configurations of TRAP₁₁+0–11 Trp, we represented the TRAP₁₁ ring as a circular one-dimensional array of zeroes or ones (e.g., 00000000000 for apo TRAP, 11111111111 for fully loaded TRAP, and 01100100000 for one of the 165 possible configurations with three bound Trp), then applied systematic rules from the NN formalisms to each configuration to obtain their energy terms. Two NN models of cooperativity were considered, which differ in whether interactions with neighboring sites are additive.

Additive NN model

An additive statistical thermodynamic model of cooperativity can be obtained from the application of occupied and unoccupied (+/−) interactions to the circular TRAP Ising lattice, and has been described previously to interpret experimental TRAP+Trp equilibrium dialysis data by Saroff and Kiefer (33). In this model, Saroff and Kiefer (33) proposed an intrinsic free energy (ΔG_i) of Trp binding that is modulated by coupling to neighboring unoccupied (ΔG_α) or occupied sites (ΔG_β). By inspecting each of the 11 binding sites and its immediate neighbors for each of the 2048 possible TRAP+nTrp configurations, aggregate free energies can be determined, yielding a partition function composed of 32 energetically distinct configurations whose energies depend on the concentration of free Trp W. Because of the relation between the binding free energy and equilibrium binding affinity, ΔG = RT ln(K), the intrinsic affinity K_i arises from the free energy ΔG_i, while the multiplicative coupling coefficients α and β are obtained from the coupling free energies ΔG_α and ΔG_β. By convention, the free energy before ligand binding is defined as the reference state, or zero. The model is additive in that it postulates that the free energy contributions from coupling to neighboring empty or occupied sites simply sum; i.e., the energy of binding to a site with no occupied neighbors is ΔG_i+2ΔG_α, a site with one occupied neighbor is ΔG_i+ΔG_α+ΔG_β, and that with two occupied neighbors is ΔG_i+2ΔG_β.

By introducing a hypothetical intrinsic affinity K_i for a site with no neighbors, the model of Saroff and Kiefer (33) suffers from mathematical correlation of its parameters. The partition function for this model, composed of three thermodynamic parameters (K_i, α, and β), can be simplified using the identities K_iα² = K₀, and β/α² = γ². This has the effect of replacing the abstract intrinsic binding free energy (ΔG_i) with a reference free energy of binding, (ΔG₀), which is the difference in free energy between the reference unbound state and a Trp-bound site flanked by two unoccupied sites, while ΔG_γ is the coupling free energy term. This restatement produces an equivalent partition function (additive nearest-neighbor (NN) model, hereafter referred to as the “NN-a” model) with the following expression with 32 unique energetic terms:

$$\Xi =1+W{K}_{0}11+W^2{K}_0^2\left(44+11\gamma \right)+W^3{K}_0^3\left(77+77\gamma +11{\gamma }^2\right)+W^4{K}_0^4\left(55+165\gamma +99{\gamma }^2+11{\gamma }^3\right)+W^5{K}_0^5\left(11+110\gamma +220{\gamma }^2+110{\gamma }^3+11{\gamma }^4\right)+W^6{K}_0^6\left(11\gamma +110{\gamma }^2+220{\gamma }^3+110{\gamma }^4+11{\gamma }^5\right)+W^7{K}_0^7\left(55{\gamma }^3+165{\gamma }^4+99{\gamma }^5+11{\gamma }^6\right)+W^8{K}_0^8\left(77{\gamma }^5+77{\gamma }^6+11{\gamma }^7\right)+W^9{K}_0^9\left(44{\gamma }^7+11{\gamma }^8\right)+W^{10}{K}_0^{10}\left(11{\gamma }^9\right)+W^{11}{K}_0^{11}{\gamma }^{11}.$$ (8)

Nonadditive NN model

In addition to the additive model (NN-a), we consider an alternative, “NN-na” model that describes interaction energies between sites as not simply a sum; that is, the coupling free energy from two occupied neighbors is not just twice that of one occupied neighbor. Such behavior could arise, for example, if binding of one ligand reduced local dynamics to such an extent that an additional ligand induces a relatively smaller degree of conformational restriction. Thus, the free energy of binding to a site flanked by 0, 1, or 2 occupied sites becomes ΔG₀, ΔG₀+ΔG_oe, and ΔG₀+ΔG_oo, respectively (oe, occupied-empty; oo, occupied-occupied, Fig. 1 D). The partition function for this nonadditive model, expressed in terms of the corresponding reference binding affinity K₀ and multiplicative factors δ and ε (from ΔG₀, ΔG_oe, and ΔG_oo, respectively), possesses a significantly greater number of nondegenerate energetic states (48 vs. 32; Fig. S11):

$$\Xi =1+W{K}_{0}11+W^2{K}_0^2\left(44+11{\delta }^2\right)+W^3{K}_0^3\left(77+77{\delta }^2+11{\delta }^2\text{E}\right)+W^4{K}_0^4\left(55+165{\delta }^2+33{\delta }^4+66{\delta }^2\text{E}+11{\delta }^2{\text{E}}^2\right)+W^5{K}_0^5\left(11+110{\delta }^2+110{\delta }^4+110{\delta }^2\text{E}+55{\delta }^2{\text{E}}^2+11{\delta }^2{\text{E}}^3+55{\delta }^4\text{E}\right)+W^6{K}_0^6\left(11{\delta }^2+44{\delta }^2\text{E}+66{\delta }^2{\text{E}}^2+44{\delta }^2{\text{E}}^3+11{\delta }^2{\text{E}}^4+66{\delta }^4+132{\delta }^4\text{E}+66{\delta }^4{\text{E}}^2+22{\delta }^6\right)+W^7{K}_0^7\left(11{\delta }^2{\text{E}}^2+33{\delta }^2{\text{E}}^3+66{\delta }^2{\text{E}}^4+11{\delta }^2{\text{E}}^5+33{\delta }^4\text{E}+99{\delta }^4{\text{E}}^2+66{\delta }^4{\text{E}}^3+11{\delta }^6+33{\delta }^6\text{E}\right)+W^8{K}_0^8\left(11{\delta }^2{\text{E}}^4+22{\delta }^2{\text{E}}^5+11{\delta }^2{\text{E}}^6+44{\delta }^4{\text{E}}^3+55{\delta }^4{\text{E}}^4+22{\delta }^6{\text{E}}^2\right)+W^9{K}_0^9\left(11{\delta }^2{\text{E}}^6+11{\delta }^2{\text{E}}^7+33{\delta }^4{\text{E}}^5\right)+W^{10}{K}_0^{10}11{\delta }^2{\text{E}}^8+W^{11}{K}_0^{11}{\text{E}}^{11}.$$ (9)

Provided one of these NN models can accurately replicate experimental observations, it has the potential to quantify the allosteric site-site coupling that arises from local ligand-dependent changes in the structure and dynamics of the protein.

Itcsimlib framework for ITC data

In a typical ITC experiment, the heat content of the cell is measured as a protein (or ligand) is titrated into ligand (or protein), and is directly related to the enthalpy change (ΔH) of the system (14, 15, 20). The affinity and stoichiometry are subsequently obtained by fitting a binding model to the integrated enthalpies at each titration point. For the NN models considered above, after the Boltzmann probability of each TRAP+nTrp configuration is obtained from its characteristic ΔG, their enthalpies can be assigned in the same way as the free energies by using the parameters ΔH_i and ΔH_γ for model NN-a, or ΔH₀, ΔH_oe, and ΔH_oo for the NN-na. This parameterization allows the binding enthalpies to differ depending on the occupancy of the neighboring identical sites. To facilitate model analysis, we developed a software library (itcsimlib) for parsing experimental ITC datasets and optimizing the parameters of phenomenological or statistical thermodynamic binding models. Itcsimlib was written in Python and makes extensive use of the SciPy scientific computation library (37). To accelerate computation, the additive and nonadditive statistical thermodynamics models themselves were written in the C programming language. Both components are available for download at http://doi.org/10.5281/zenodo.159716.

Data collection

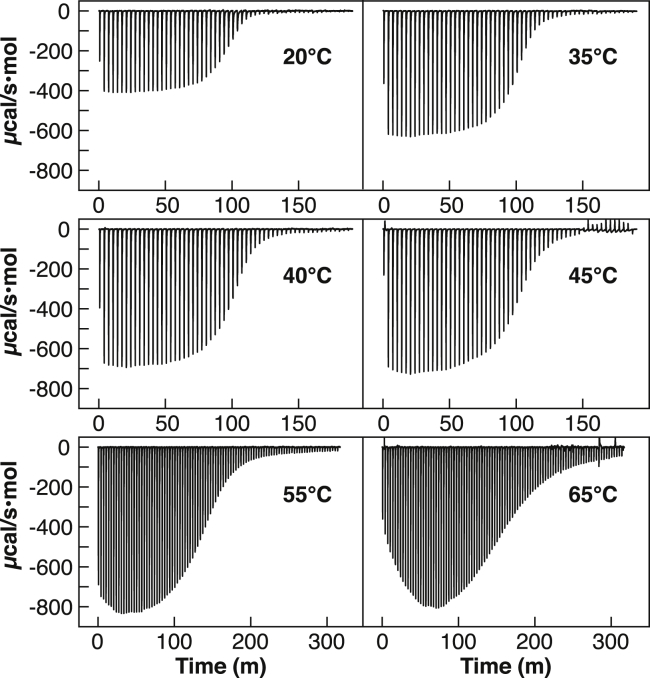
ITC isotherms were obtained by titrating L-tryptophan into 75 μM Bst A28I TRAP at six temperatures: 20, 35, 40, 45, 55, and 65°C (Fig. 2); scanning calorimetry experiments indicate that TRAP denaturation occurs well above these temperatures (27, 44). The resulting integrated enthalpies, ΔH_obs, at each titration point were then used as the experimental data for restraining the two statistical thermodynamic models. Individually, each of these experimental datasets could be fit well using a phenomenological model consisting of two independent binding modes. However, in addition to only providing bulk-average descriptions of binding energetics, such a typical analysis neglects the improved precision and insight available by globally fitting across multiple experimental conditions (in this case, temperature).

Figure 2.

Calorimetric isotherms obtained by titrating Trp into TRAP at different experimental temperatures reveal multimode, cooperative binding, with different K_d, ΔH, and ΔC_p, although at lower temperatures those features cannot be discerned.

Fitting of ITC data to a phenomenological two-site model

Global fitting of the six datasets was achieved by minimizing the reduced χ² between the experimental datasets and the fit generated by the model at each of the experimental conditions. This required the consideration of the change in heat capacity associated with binding, ΔC_p, and its effects on the temperature dependence of ΔG and ΔH terms. The inclusion of ΔC_p is a significant added benefit of global fitting, as it provides structural information, namely on the exclusion (or inclusion) of solvent as part of the binding event, and changes in protein structure (17, 18). For binding processes with a temperature-independent ΔC_p, the temperature dependence of enthalpic, entropic, and free energy terms are well defined (18, 19, 47):

$$\begin{array}{c}\Delta H\left(T\right)=\Delta H\left(T_{\text{ref}}\right)+\Delta C_p\left(T-T_{\text{ref}}\right)\\ \Delta S\left(T\right)=\Delta S\left(T_{\text{ref}}\right)+\Delta C_p\text{ln}\left(T/T_{\text{ref}}\right)\\ \Delta G\left(T\right)=\Delta H\left(T_{\text{ref}}\right)-T\Delta S\left(T_{\text{ref}}\right)+\Delta C_p\left[\left(T-T_{\text{ref}}\right)-T\text{ln}\left(T/T_{\text{ref}}\right)\right].\end{array}$$ (10)

First, we performed a global fit of the six experimental isotherms using a derivation of a common (35) phenomenological two-site binding model comprising eight parameters (n₁, ΔG₁, ΔH₁, ΔC_p,1 and n₂, ΔG₂, ΔH₂, ΔC_p,2). This model describes two independent binding modes with variable stoichiometry n:

$$\begin{array}{l}Q=n_1{\Theta }_1\Delta H_1+n_2{\Theta }_2\Delta H_2,\\ K_1=\frac{{\Theta }_1}{\left(1-{\Theta }_1\right)\left[W\right]}=\text{exp}\left(\frac{-\Delta G_1}{RT}\right),\\ K_2=\frac{{\Theta }_2}{\left(1-{\Theta }_2\right)\left[W\right]}=\text{exp}\left(\frac{-\Delta G_2}{RT}\right),\end{array}$$ (11)

where Q is per-molar heat content of the system, Θ is the fractional saturation of each mode, and R is the universal gas constant.

Although this two-site model provided qualitatively acceptable fits to the experimental data (Fig. S4), its mechanistic ambiguity limits interpretation of the resulting parameters (n₁ = 2.5, ΔG₁ = −9.2 kcal/mol, ΔH₁ = −13.2 kcal/mol, ΔC_p,1 = +480 cal/mol/K, n₂ = 8.2, ΔG₂ = −9.3 kcal/mol, ΔH₂ = −20.4 kcal/mol, and ΔC_p,2 = −650 cal/mol/K). Indeed, the large positive ΔC_p,1 of +480 cal mol⁻¹ K⁻¹ is unusual for ligand binding processes (18, 19, 47). However, fitting to this two-site model enables comparison to existing phenomenological observations: specifically, the resulting fits suggest a nominal ΔG of ∼−9.2 kcal/mol for both binding modes, which corresponds to a K_d,obs of 0.4 μM at 40°C, agreeing with previous measurements on both wild-type TRAP and its A28I mutant (27). A model composed of three independent binding modes was also evaluated, but this expansion did not significantly improve fit quality.

Global fitting to NN mechanistic models

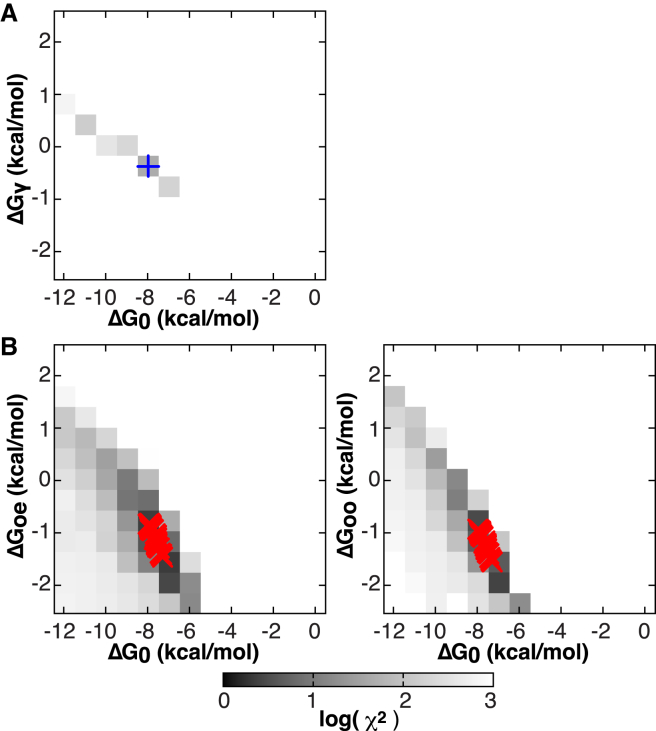
We next compared the ability of the NN models to globally fit the available isotherms. When optimizing models with many parameters against experimental data (48, 49, 50), numerical algorithms can converge to local minima, and/or parameters may be highly correlated, limiting both accuracy and precision (39, 49, 50). To evaluate these issues, the free energy parameters for the proposed statistical thermodynamics models were systematically sampled across several two-dimensional grids: ΔG₀ versus ΔG_γ for the additive NN-a model (Fig. 3 A), and ΔG₀ versus ΔG_oe and ΔG₀ versus ΔG_oo for the NN-na model (Fig. 3 B). The remaining ΔH and ΔC_p parameters for each model were then freely optimized.

Figure 3.

Binding free energy parameter grids used to reduce parameter search space and identify χ² minima. (A) Grid of coupling free energy (ΔG_γ) versus the free energy of binding to a reference state with no occupied neighbors (ΔG₀), for the six-parameter additive model. (Blue cross) Global minimum. (B) Coupling free energies for the nine-parameter model of nonadditive cooperativity, of sites flanked by one (ΔG_oe) and two (ΔG_oo) occupied neighboring sites, versus the reference state ΔG₀. (Red crosses) Values of fits to 50 random bootstrap datasets were used to estimate parameter uncertainties, using the grid minimum as a starting point. To see this figure in color, go online.

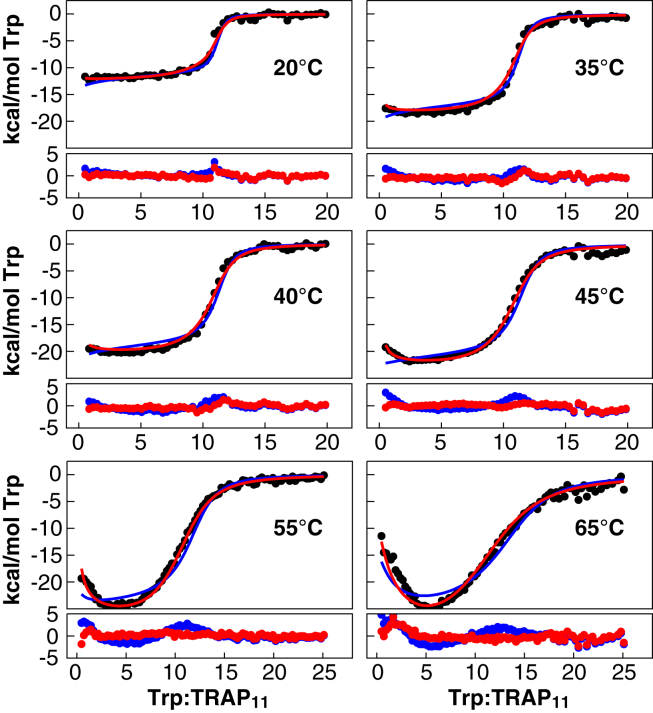
This grid fitting procedure yielded a global χ² minimum for the six-parameter (two sets of ΔG, ΔH, and ΔC_p values) NN-a model, with a reference free energy ΔG₀ of −8 kcal mol⁻¹ and coupling free energy ΔG_γ of −0.5 kcal mol⁻¹, indicative of weak positive cooperativity (Fig. 3 B; Table S1). However, this model demonstrated relatively poor agreement with the experimental data (Fig. 4; reduced χ² = 7.1) with residuals that deviate systematically from the observed values both early and late in the titration (Fig. 4).

Figure 4.

Nonadditive nearest-neighbor model provides a superior global fit to experimental data. Integrated enthalpic heats per injection (black circles) at different temperatures are globally fit using the additive model NN-a (blue, χ² = 7.1) and nonadditive model NN-na (red, χ² = 1.8). The resulting residuals from each fit are shown below each isotherm. To see this figure in color, go online.

The nonadditive NN-na model, defined by three sets of ΔG, ΔH, and ΔC_p values (Fig. 3 C), also yielded an apparent global minimum on the two systematically sampled grids for its ΔG parameters. In addition to these two-dimensional grid fits, the one-dimensional χ² error surfaces for each of the nine parameters reveal well-defined minima (Figs. S6–S8). After fit convergence, model NN-na provides substantially better agreement to the experimental data (reduced χ² = 1.8, Fig. 4), and more uniformly distributed residuals. The resulting optimized parameters indicate positive cooperativity (Tables 1 and S2; Fig. S5), suggesting that Trp binding to a site flanked by empty sites occurs relatively weakly (ΔG₀ = −8 kcal mol⁻¹ at 40°C; K_d = 4 μM), while having one flanking occupied site stabilizes binding by ∼13% (1 kcal mol⁻¹; K_d = 0.8 μM at 40°C). Finally, binding to a site flanked by two occupied sites is only slightly more favored (15% greater ΔG), with a K_d of 0.7 μM.

Table 1.

Best-fit Parameters for NN-na Model of Trp Cooperativity

NN	ΔGcoupling	ΔGbind	ΔHcoupling	ΔHbind	ΔCp,coupling	ΔCp,bind	Kd
	kcal mol−1		kcal mol−1		kcal mol−1 K−1		μM
0	—	−7.70 ± 0.21a	—	−13.5 ± 1.4a	—	0.10 ± 0.10a	4.24 ± 0.12
1	−1.04 ± 0.22a	−8.74 ± 0.21	−6.11 ± 1.0a	−19.7 ± 1.2	−0.49 ± 0.10a	−0.39 ± 0.10	0.80 ± 0.24
2	−1.15 ± 0.22a	−8.85 ± 0.21	−4.67 ± 1.4a	−18.2 ± 1.4	−0.45 ± 0.11a	−0.39 ± 0.10	0.67 ± 0.18

Globally fit parameters are given at a reference temperature of 40°C (313.15 K). Confidence intervals were obtained via bootstrapping with 200 replicates. NN, number of occupied nearest neighbors. Unless otherwise indicated, terms were obtained from the sum of the reference state (e.g., ΔG₀) and coupling terms (e.g., ΔG_oe and ΔG_oo). Equilibrium constants from ΔG_bind = RT ln K_d at 40°C.

^aFitted term.

The best fit parameters for the NN-na model indicate that initial binding to sites flanked by two empty neighbors is enthalpically driven at 40°C, with a ΔH₀ of −14 kcal mol⁻¹, and binding to sites flanked by one and two occupied neighbors is stabilized by additional enthalpic effects of −6.1 and −4.7 kcal mol⁻¹, respectively. Correspondingly, at 40°C binding is entropically disfavored, with a ΔS of −18.5 cal mol⁻¹ K⁻¹ for a site with empty neighbors, and −34.7 and −29.8 cal mol⁻¹ K⁻¹ for one and two occupied neighbors, respectively; these reveal a higher entropic penalty to binding to sites with one occupied neighbor, but slightly lower penalty for a site with two occupied neighbors.

Limitations

Implementation of this mechanistic fitting approach has several requirements. First, and foremost, a suitably constrained mechanistic model must be posed such that a binding polynomial can be constructed and tested during global fitting. Second, discrete binding modes must display distinct thermodynamic behavior over experimentally accessible conditions. For temperature-dependent binding data in particular, we would expect that ΔC_p values unique to each binding mode would provide the highest resolving power, while also being most mechanistically informative about differences in those binding modes. It follows that successful implementation would depend on those ΔC_p values being sufficiently different to generate distinguishable effects on ΔH over experimentally accessible temperature ranges, and being relatively temperature-independent over that range. Lastly, like most multivariate fitting, fitness metrics are better used for comparing alternative models than for establishing whether a particular model is “right”.

Trp binding trajectory

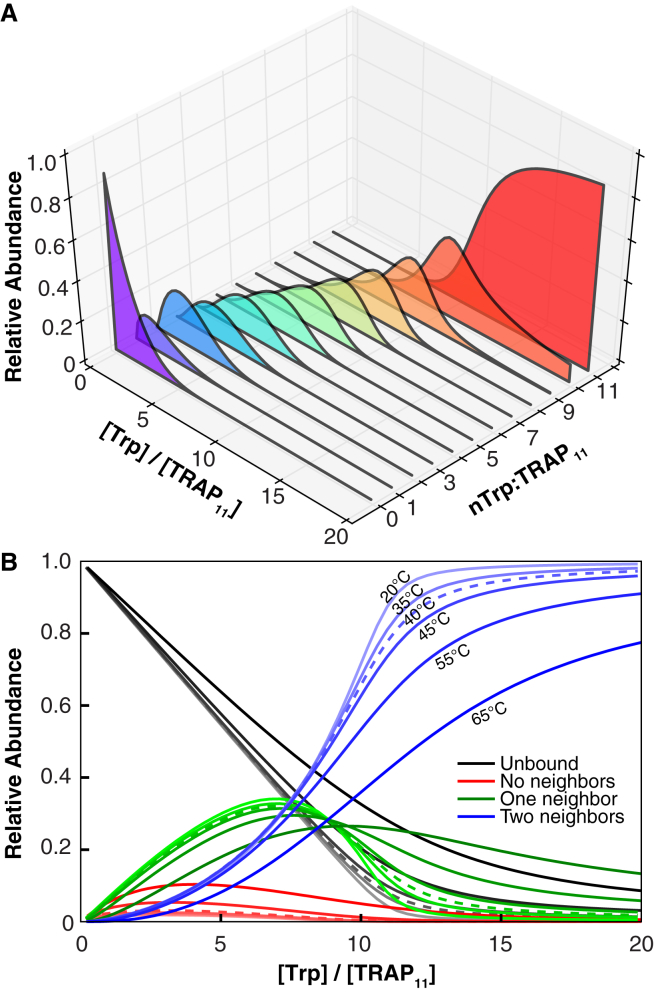
The partition functions for the NN models allow computation of the population of TRAP₁₁+nTrp species at arbitrary concentrations, thus predicting features of the Trp-dependent behavior of TRAP (Figs. 5, S9, S10, and S12). As a consequence of the stabilizing effect of having a bound neighbor, the NN-na model predicts that TRAP species with only one Trp bound are disfavored relative to those with none or two sites bound. In contrast, the small additional benefit to having two bound neighbors does not similarly bias the populations when comparing rings with two versus three bound Trp (Fig. 5). In addition, the most energetically favorable configurations (i.e., those with the lowest free energy), are not necessarily the most abundant because their reduced statistical weights may make them less probable. Instead, for TRAP species with 4 to 9 Trp per TRAP, the second most energetically favorable configurations are most abundant, due to their consistently greater statistical weights (Eq. 9).

Figure 5.

Populations of Trp+TRAP species during the ITC titration predicted by the nonadditive model using the best-fit parameters from Table 1. (A) The relative abundance at each titration point, of TRAP₁₁ species with 0–11 bound Trp, colored purple to red for the ITC titration experiment performed at 40°C (starting TRAP₁₁ concentration = 6.81 μM). (B) The relative abundance of empty sites (black), occupied sites with no bound neighbors (red), occupied sites with one bound neighbor (green), and occupied sites with two bound neighbors (blue), as a function of Trp/TRAP ratio during ITC titrations over a range of temperatures. To see this figure in color, go online.

Examining whether individual bound sites have bound neighbors (Fig. 5 B) reveals that occupied sites without any bound neighbors never exceed >10% of all sites. This supports the intuition that cooperativity favors clusters of pairs of occupied sites (Fig. S11). This may have important functional implications: if TRAP binds its cognate mRNAs by an initial weak encounter with a single GAG repeat to an activated pair of protomers, followed by a rapid binding of additional tandem GAG repeats to adjacent activated TRAP protomers, the clustering of activated TRAP subunits may permit high-affinity RNA binding by incompletely saturated TRAP oligomers. Indeed, five sequential GAG triplets bound to activated TRAP subunits are sufficient for low nanomolar binding affinities (51). This may also explain observations that relatively small amounts of wild-type TRAP subunits in a context of inactivatable mutant protomers nevertheless enable robust RNA binding (52).

Comparison to Hill analysis

From the population trajectories computed from the partition function of model NN-na, we simulated Hill analysis to provide a qualitative comparison of the two approaches. Hill analysis is typically performed by precomputing a fractional saturation Θ from some experimental observable, then fitting either Θ versus [L] (free ligand concentration), or log [Θ/(1 − Θ)] versus log [L] to either nonlinear or linearized forms of the Hill equation. Saturation plots of predicted site occupancy at each temperature across the experimental concentrations of free ligand illustrate the difficulty of quantifying cooperative behavior via traditional Hill analysis, even with unrealistically low experimental uncertainties of 1% (Fig. S13). Fitting the population trajectories using the Hill expression yielded a temperature-dependent apparent K_D ranging from of 0.1 μM at 20°C to 10 μM at 55°C, and weakly positive Hill coefficients ranging from 1.4 to 1.6 over the same temperature range (Fig. S14). These values, reflecting slight-to-modest cooperativity, are generally consistent with the results of previous attempts to quantify cooperativity in TRAP, while also being devoid of mechanistic insight.

Structural insights

Heat capacity changes ΔC_p associated with Trp binding provide a means to quantify changes in accessible protein-solvent conformational states (18, 19, 47, 53, 54), and have the potential to provide rich insights into structure-thermodynamic relationships. Best fit parameters for model NN-na (Tables 1 and S2; Fig. S5) indicate that binding of Trp to a site with empty neighbors is associated with a negligible ΔC_p,0, while structure-based surface area calculations suggested an expected ΔC_p of −0.088 kcal mol⁻¹ K⁻¹ for burial of a Trp within its binding site on TRAP (27). Trp binding to sites with one or two occupied neighbors is associated with large negative ΔC_p,oe, ΔC_p,oo values of −0.49, and −0.46 kcal mol⁻¹ K⁻¹. These are comparable to the value of −0.37 kcal mol⁻¹ K⁻¹ obtained for Trp binding to wild-type TRAP, the excess of which might be explained by binding-coupled folding of ∼19 residues. Because the burial of nonpolar residues and binding-linked structural changes both contribute to a negative ΔC_p, these findings suggest that binding to sites with no occupied neighbors does not result in significant structural rearrangement, while the small negative ΔC_p from solvent release is offset by additional roughness in the protein-solvent free energy landscape. However, the large ΔC_p,oe and ΔC_p,oe do reflect structural rearrangement and reduction in the number of thermally accessible protein-solvent states.

Conclusions

These observations allow us to propose a mechanism for cooperative Trp binding to TRAP. Initial weak binding by some Trp molecules to isolated sites provides a metastable platform for opportunistic binding by additional Trp, upon which the protein-ligand-solvent system becomes more ordered and compact, adopting a hololike state. Once two-to-three pairs of NN interactions are formed (i.e., four-to-six bound Trp), there is little additional change in the protein structure upon additional Trp binding. This microscopically informed result is consistent with a phenomenological kinetic analysis of Trp binding to A28I TRAP through stopped-flow fluorescence that was best fit by a two-step pathway, in which an initial Trp binding step with a fast release rate enables a second, high-affinity Trp binding mode characterized by a greatly retarded Trp release rate (28). While direct application of a mechanistically informed NN model to analysis of the kinetic data are beyond the scope of this work, the results presented here provide compelling microscopic detail to explain that phenomenological observation.

Oligomeric proteins are prevalent across biology (55, 56, 57), and their overrepresentation in regulatory systems (58, 59) highlights the importance of an inter-subunit communication fine-tuning function. Compared to hemoglobin, which is the best studied model of cooperativity, the tryptophan binding behavior of TRAP presents several unique challenges, including the large number of ligand binding sites. Unlike the 16 possible and until very recently experimentally indistinguishable configurations of hemoglobin (60), the >100 potentially energetically distinct states of TRAP provide a daunting conceptual and logistical conundrum.

Commonly used phenomenological models represent a fundamentally unrealistic oversimplification of a binding mechanism, and thus are limited in the amount of information that can be extracted from binding data. Here, we explored application of mechanistically informed statistical thermodynamic models, and global analysis, to obtain microscopic thermodynamic parameters from bulk thermodynamic experiments. In the case of Bst A28I TRAP, our data quantify the energetic coupling between sites and indicate that site-site communication between the sites is not simply additive, such that having one neighboring Trp induces almost as much structuring as having two neighboring Trp. These findings advance our understanding of the TRAP biosensor and provide insights into the microscopic origins of cooperativity. Although unique to bacilli, TRAP represents a common and important class of allosteric proteins both in its quaternary structure and dynamic behavior; we expect the approach outlined here to be generally applicable to, and informative for, other multimeric allosteric systems.

The approach outlined here provides deeper insight into Trp-TRAP interactions and argues for broader use of mechanistically informed models when fitting and interpreting thermodynamic binding data (20, 61). The Hill equation and Hill coefficient remain in common use in the biochemistry literature, in large part because it is generally easy to measure, and provides some qualitative metric for comparison. However, its limited mechanistic value should discourage quantitative use and interpretation (7, 8). In contrast, the tools of structural biology, statistical thermodynamics, and mathematical modeling of mechanisms have the potential to take us beyond phenomenological treatments of allostery to an understanding of its microscopic origins and mechanisms (4, 62, 63, 64).

Author Contributions

E.C.I., I.R.K., P.G., and M.P.F. designed and performed the research, and analyzed data; and E.C.I., I.R.K., and M.P.F. wrote the article.

Editor: David Eliezer.