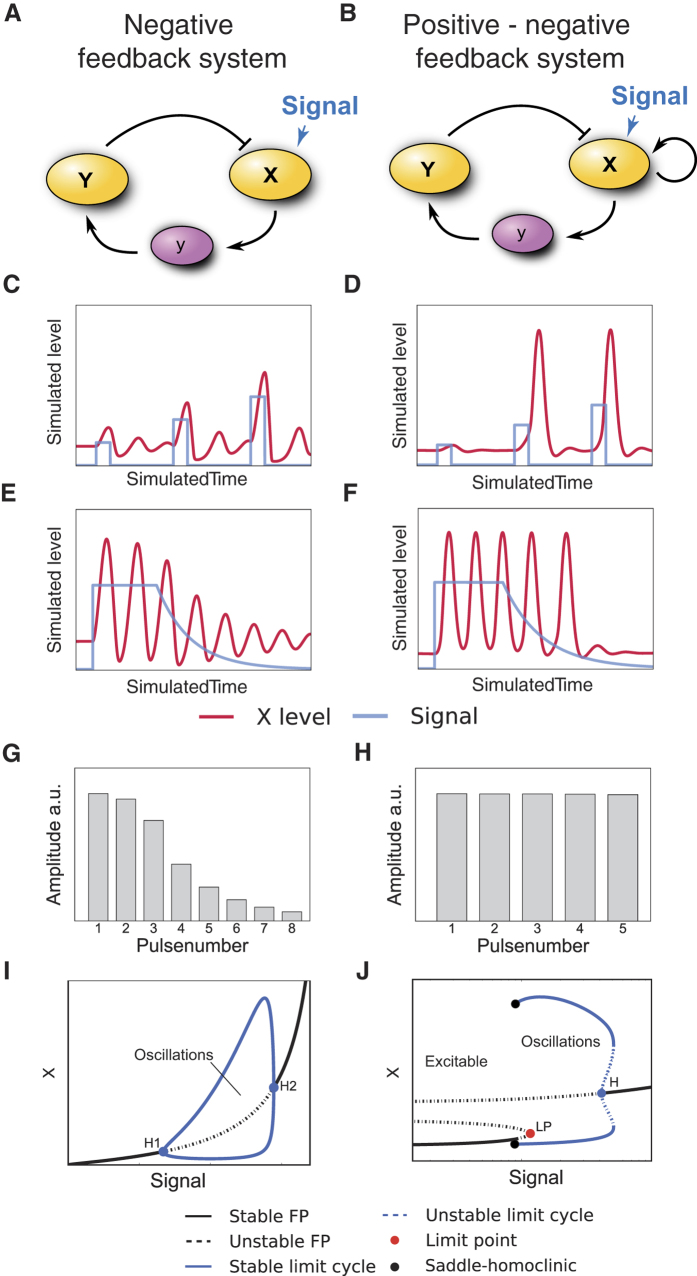
Figure 2. Regulatory network topology constrains dynamic stimulus responses.

(A,B) Interaction graphs of hypothetical systems comprising only negative feedback (NF, A) or combined negative and positive feedbacks (NPF, B). The positive feedback is realized by a positive self-interaction. (C,D) Time-resolved response of the NF (C) and NPF (D) systems to transient signals of increasing strengths. (E–H) Time courses demonstrating the termination of oscillations during dynamic switching after sustained stimulation for the NF (E) and NPF (F) system. The corresponding amplitudes of the oscillation were quantified for individual peaks (G and H). Subthreshold responses were excluded. (I) Bifurcation diagram of the NF system for varying signal strengths. The oscillatory regime is confined by two supercritical Hopf bifurcations (H1 and H2). The amplitudes of the limit cycle oscillations are indicated by the blue line. (J) Bifurcation diagram of the NPF system for varying signal strengths. The system is excitable for low input signals. For higher signal strengths a limit cycle is born with large amplitudes around the saddle-homoclinic bifurcation. The stable rest state subsequently disappears via a saddle-node bifurcation (LP).