Simulation-Based Evaluation of Hybridization Network Reconstruction Methods in the Presence of Incomplete Lineage Sorting

Abstract

Hybridization events generate reticulate species relationships, giving rise to species networks rather than species trees. We report a comparative study of consensus, maximum parsimony, and maximum likelihood methods of species network reconstruction using gene trees simulated assuming a known species history. We evaluate the role of the divergence time between species involved in a hybridization event, the relative contributions of the hybridizing species, and the error in gene tree estimation. When gene tree discordance is mostly due to hybridization and not due to incomplete lineage sorting (ILS), most of the methods can detect even highly skewed hybridization events between highly divergent species. For recent divergences between hybridizing species, when the influence of ILS is sufficiently high, likelihood methods outperform parsimony and consensus methods, which erroneously identify extra hybridizations. The more sophisticated likelihood methods, however, are affected by gene tree errors to a greater extent than are consensus and parsimony.

Introduction

Evolutionary processes allowing the transmission of genetic information horizontally among species include horizontal gene transfer^1–3 and hybridization.^4,5 Hybridization is particularly important in the evolution of eukaryotic species by hybrid speciation: when 2 genetically isolated parental species hybridize to produce a new hybrid lineage.⁶ In homoploid hybridization, the hybrid species has the same ploidy level as the parental species. Owing to the recombination process, after the first hybrid generation, the genome of a homoploid hybrid becomes a mosaic, with different regions tracing distinct evolutionary histories of the parental species. Hybrid speciation might also result in a polyploid hybrid species: sets of chromosomes in polyploid genomes inherited from distinct parents—homeologous chromosomes—have distinct histories that follow the distinct histories of the parental lineages.

In phylogenetic studies of species involved in hybridizations, evolutionary relationships are more easily accommodated using a concept that generalizes the commonly used concept of a species tree: species networks.^7,8 Genomic segments evolve in a species network model just as they do in species tree models, except that for some lineages, several alternative paths to the common ancestor are possible.

A number of consensus, parsimony, and likelihood-based methods that can be used for inferring species networks from sets of multiple gene trees have been developed. In consensus-based species network methods, analogously to species tree inference using consensus,⁹ clades, or clusters defined by clades, that appear in a minimal percentage of gene trees are displayed in the form of a network.¹⁰ The consensus approach is often used for visualization and identification of contradictory phylogenetic evidence without distinguishing among multiple potential causes of the discordance, including in scenarios in which hybridization is of interest.^11,12 Because many ways exist to produce a network from a collection of clusters, several consensus methods have been developed,^13–15 accommodating such phenomena as variability of taxon sampling across gene trees,¹⁶ which arises when some taxa are missing orthologs for some of the phylogenetic characters due to gene loss or failure to detect the genes.

A parsimony-based method for inferring species networks from a collection of gene trees has been reported by Yu et al,¹⁷ extending the minimizing-deep-coalescence (MDC) criterion for species tree inference.^18,19 In MDC-based species tree inference, the species tree requiring the fewest deep coalescence events to explain the discordance of gene tree topologies is reported as the estimated species tree. In its extension for species network inference, a species network is represented as a multilabeled species tree,²⁰ and the multilabeled species tree that minimizes deep coalescence events is inferred using a set of possible mappings of gene tree tips onto tips of the multilabeled species tree representation, thereby producing an MDC species network.

In a maximum likelihood (ML) framework, one approach infers species networks from a set of gene trees.^21,22 It uses a multilabeled tree representation of the species network, similar to the maximum parsimony (MP) method of Yu et al,¹⁷ to calculate under a coalescent model the probabilities of gene trees, given the topology and branch lengths of the species tree.²³ All possible mappings of the gene tree leaves to tips of the multilabeled species tree are considered in evaluating gene tree probabilities. The likelihood of the multilabeled species tree is built as a product across loci of gene tree probabilities and maximized over a space of species networks, including both topology and branch lengths, but constrained by a maximal permitted number of hybridizations. With this method, a strategy can be implemented in which species networks allowing different numbers of hybridizations are constructed on the same set of gene trees and compared using the Akaike information criterion (AIC) or related statistics.

Given a set of gene trees, a second ML method tests whether a hybridization event between a pair of extant sister lineages is more likely than incomplete lineage sorting (ILS) to explain the gene tree discordance involving a putative extant hybrid species.^24,25 A species network containing 1 candidate hybridization event is represented as a superposition of 2 alternative species trees, conditional on which loci evolve as in a regular species tree. Assuming conditional independence of loci given the species network, under a multispecies coalescent model, the likelihood of the species network is as follows:

$$L\left(\alpha ,t|S,g,\theta \right)={\displaystyle \prod _{j=1}^{\text{N}}\left[\left(1-\alpha \right)f_G\left(g_j|\theta ,S_1,t\right)+\alpha f_G\left(g_j|\theta ,S_2,t\right)\right]}$$ (1)

where α is the relative contribution of 1 species tree topology to the network and t is a vector containing the species tree branch lengths. θ is a vector of population sizes for branches of the species tree, N is the number of loci, g is the set of gene trees, possibly including intraspecific sampling, S₁ and S₂ are species trees representing a species network S with 1 hybridization, and f_G is the probability of a gene tree—both topology and branch lengths—given the species tree topology and branch lengths under the multispecies coalescent.²⁶ This model is compared using AIC with the nested submodels in which α is set to 0 or 1.

In the case of species tree inference methods, performance depends on a number of factors, including the number of loci in the multilocus data set used, the evolutionary distances separating taxa in the species tree, the size and topology of the species tree, the number of alleles sampled per species, and the accuracy of gene tree inference and orthology prediction.^27–29 The behavior of methods for species network inference is likely to vary as a function of analogous properties.

For individual methods, simulations have examined various aspects of the dependence of hybridization network inference on factors of interest. For example, the MP method of Yu et al¹⁷ was generally able to recover true network topology and inheritance probability α when the true number of hybridization events in the event history was supplied, and network branches adjacent to hybridizations were set to at least 1 coalescent time unit. The ML method of Kubatko²⁴ was tested on species networks with lengths set to 1 coalescent unit for branches separating consecutive speciation or hybridization events. The ability of the method to detect true hybridizations in a model-testing framework improved when the number of sampled loci increased from 20 to 100.

With the recent increased interest in hybridization, analyses of the performance of the various methods can help users in their choice of method and in understanding potential strengths and weaknesses of such methods. Newly introduced methods for species network inference under hybridization have generally been evaluated on different scenarios, however, and little comparative data exist on relative performance. Moreover, simulation studies have explored a relatively limited portion of the parameter space, often using longer species network branch lengths that do not provide as great a challenge to methods as smaller values. Here, we report a systematic simulation–based comparison of methods for species network inference, investigating the influence of species divergence time, species contributions to hybridization events, and errors in gene tree estimation on the performance of several inference methods.

Materials and Methods

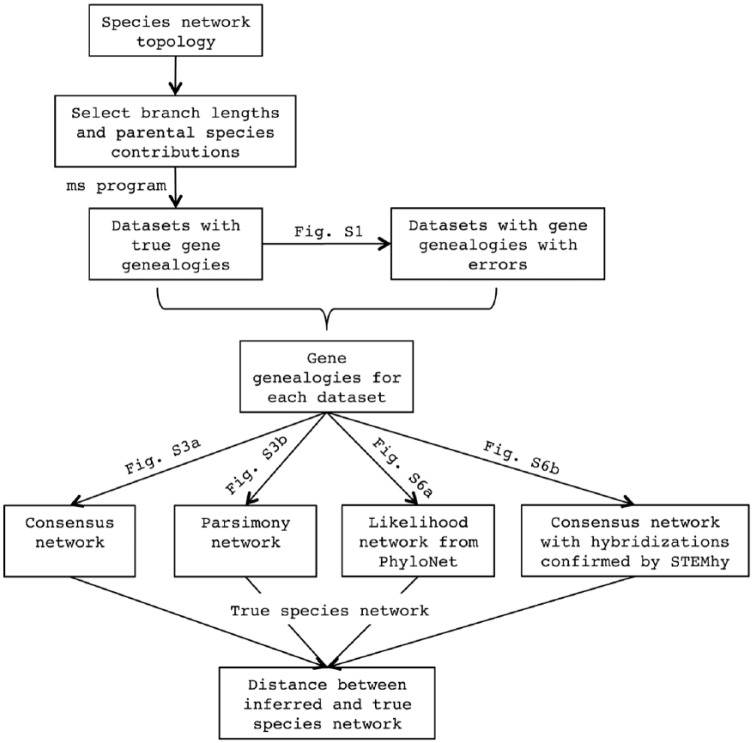
We use simulations to study the performance of methods for inferring species trees and networks. For our pipeline (Figure 1), first, we choose parameters of the species network—we select a particular species network topology and choose parameter values for the branch lengths and parental species contributions toward hybridization. Second, we simulate gene genealogies—for each set of species network parameter values, we generate gene genealogies conditional on the species network, considering sets of size 10 to 250 gene trees, with 10 replicates for each size. Third, we introduce errors into true gene trees—for some parameter settings, we also add errors to true gene genealogies, forming sets of erroneous gene trees with different error rates. Fourth, we reconstruct species trees and species networks—using each set of gene genealogies, we employ each of a series of methods for inferring species relationships, both species tree and network inference methods. Finally, we evaluate inferred species histories—to assess the performance of methods, we compare the inferred species tree or network with the true species relationships, both on average and in the standard error across 10 replicates.

Figure 1.

Workflow for the analysis.

Choosing parameters of the species network

We designed a scenario of species evolution in which 1 hybridization event occurs (Figure 2), incorporating speciation events both before and after hybridization. For the fixed network topology, we varied the network branch lengths and the parental species contributions to the hybridization event. Different combinations of these parameter values generated 18 evolutionary scenarios, to each of which we assigned a numerical label (Table 1).

Figure 2.

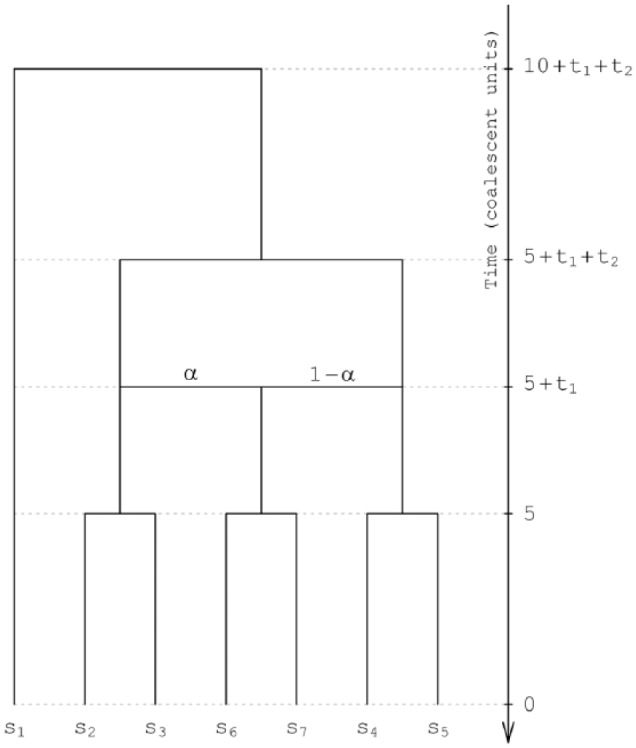
Species network topology used to simulate gene genealogies. α and 1 − α denote the contributions of 2 parental species toward a hybridization event. Branch lengths in the network are measured in coalescent units, with 1 unit equal to the number of generations required on average for 2 random alleles in a population to find their common ancestor. The species are labeled s₁ to s₇.

Table 1.

Parameter values for simulated data sets.

Scenario	t 1 a	t 2 a	αb	Gene tree error
1	0.025	0.025	0	None
2	0.025	0.025	.1	None
3	0.025	0.025	.2	None
4	0.025	0.025	.5	None
5	0.025	0.25	.5	None
6	0.025	2.5	.5	None
7	0.25	0.025	.5	None
8	0.25	0.25	0	None
9	0.25	0.25	.1	None
10	0.25	0.25	.2	None
11	0.25	0.25	.5	None
12	0.25	2.5	.5	None
13	2.5	0.025	.5	None
14	2.5	0.25	.5	None
15	2.5	2.5	0	None
16	2.5	2.5	.1	None
17	2.5	2.5	.2	None
18	2.5	2.5	.5	None
19	0.025	0.025	.5	Lowc
20	0.025	0.025	.5	Mediumd
21	0.025	0.025	.5	Highe
22	0.25	0.25	.5	Lowc
23	0.25	0.25	.5	Mediumd
24	0.25	0.25	.5	Highe
25	2.5	2.5	.5	Lowc
26	2.5	2.5	.5	Mediumd
27	2.5	2.5	.5	Highe

^at₁ and t₂ measured in coalescent units are branch lengths of the network used in simulation (Figure 2).

^bα denotes the contribution of one parental species lineage toward the hybridization event. The other parental species contributes at a level of 1 − α.

^cErrors added to the distance matrix were drawn from a normal distribution N(0, 0.2).

^dErrors added to the distance matrix were drawn from a normal distribution N(0, 1).

^eErrors added to the distance matrix were drawn from a normal distribution N(0, 5). Results for particular scenarios are in some cases copied between multiple figures to emphasize different comparisons.

We varied the extent to which ILS affects gene trees by considering several settings for the branch lengths, measured in number of generations normalized by the effective number of gene copies in a population, or coalescent time units. Viewed forward in time, we set the branch lengths of species network edges leading to the ancestral species participating in hybridization (t₂) and to the first speciation event after hybridization (t₁) to 0.025, 0.25, or 2.5, and we set the branch lengths of the edges leading to the extant species and from the species network root to 5 (Figure 2). As internal species network branch lengths become shorter, ILS increases, gene tree topologies deviate from the species tree topology more frequently, and the experimental settings provide more challenging scenarios for determining species relationships.

Each hybridization event is characterized by the relative contributions of the 2 parental species toward the event, α and 1 − α. We varied the value of α, considering α = 0, .1, .2, and .5 (Table 1). These 4 values of α represent 4 levels of hybridization: no hybridization, “skewed” hybridizations with different genetic contributions of the 2 parents to the hybrid at each of 2 levels, and symmetric hybridization with equal genetic contributions of the 2 parents to the hybrid. We expect that skewed hybridizations will be generally harder to detect, as fewer loci in the data set will record the transmission of the minor contributing genome. Use of α = 0 assists in quantifying the extent to which a hybridization hypothesis is supported when hybridization is not included in the true scenario of species evolution.

Simulating gene genealogies

For each of our 18 evolutionary scenarios (Table 1), we used the MS program³⁰ to generate gene trees conditional on the species network, sampling 1 allele per species for each gene, assuming that the organisms are haploid. All gene trees were simulated independently, and gene trees for different settings for the number of loci were distinct.

Introducing errors into true gene trees

To assess the robustness of species tree and network inference methods to evaluate errors in gene tree estimation, we generated several sets of erroneous gene trees using gene genealogies from scenarios 4, 11, and 18, where branch lengths t₁ and t₂ were set to equal values, and α = .5. The pipeline for this simulation appears in Figure S1. The simulation adds noise to the original gene trees produced with MS for these settings. For each gene tree, we computed the pairwise distances between leaves of the gene tree as the sum of the lengths of all branches on the shortest path between the leaves. Next, to emulate the errors in genetic distance estimation, each entry of the branch length distance matrix was perturbed by adding a random number drawn from a normal distribution of specified variance centered at 0, and neighbor-joining trees were constructed using perturbed distance matrices. Distance methods such as neighbor joining sometimes infer negative branch lengths³¹; in addition, in this case, negative branch lengths might also rise from negative entries in the perturbed distance matrices. If negative lengths were inferred, then each negative value was replaced with a small nonzero value of 0.000001. Normal distributions with different variances, N(0, 0.2), N(0, 1), or N(0, 5), were used to account for low, medium, and high error rates in gene tree estimation. This procedure generated additional sets of gene genealogies that we considered as different scenarios (scenarios 19-27, Table 1).

Reconstructing species trees

Species tree inference methods are routinely used to analyze species phylogenies, even in cases when species under consideration are known to hybridize. For completeness, to evaluate the effect of a hybridization event on species tree estimation, we included 2 methods for species tree reconstruction (Table 2): greedy consensus⁹ and MDC,¹⁹ as implemented in the PhyloNet_3.5.4 package.³²

Table 2.

Methods evaluated in this study.

Form of estimate	Type of method	Reference	Inference framework	Software	Evolutionary processes considered	Notes
Tree	MDC tree	Than and Nakhleh19	Maximum parsimony	PhyloNet	ILS
Tree	Greedy consensus tree	Bryant9; Felsenstein33	Consensus	PhyloNet
Network	Consensus network	Holland and Moulton10	Consensus	Dendroscope		Requires threshold for percentage of trees containing the cluster for the cluster to be included in the network
Network	MP network, PhyloNet	Yu et al17	Maximum parsimony	PhyloNet	ILS, hybridization	Number of hybridization events needs to be set
Network	ML network, PhyloNet	Yu et al22	Maximum likelihood	PhyloNet	ILS, hybridization	Number of hybridization events needs to be set; AIC to test different models
Network	ML network, STEM-hy	Kubatko24	Maximum likelihood	STEM-hy	ILS, hybridization	Only allows testing of candidate hybridization events; AIC to test different models

Abbreviations: AIC, Akaike information criterion; ILS, incomplete lineage sorting; MDC, minimizing deep coalescence; ML, maximum likelihood; MP, maximum parsimony.

Reconstructing species networks

We tested 4 methods for species network inference (Table 2). For some of the methods, we first conducted initial experiments using the largest sets of gene genealogies from evolutionary scenarios 1 to 4, 8 to 11, and 15 to 18 to establish a generally applicable strategy for species network inference with the method. The largest sets of gene genealogies were used to inform protocol design with as much phylogenetic signal as possible. We then used the protocols to infer species networks in all the experiments.

Consensus

In consensus species network inference, a collection of gene trees is summarized in a form of a network. The network displays clusters of extant taxa that appear in gene trees, as well as the number of gene trees displaying each of the clusters. Clusters displayed by a minimal percentage of the entire gene tree collection appear in the inferred network.^10,14 The choice of the percent threshold on the number of gene trees is a methodological decision made by the user.

To decide on a threshold to routinely apply to our experiments, we reconstructed consensus networks on sets of 250 gene genealogies from scenarios 1 to 4, 8 to 11, and 15 to 18 by setting the percent threshold to 8% to 50%, with a step of 2%, recording the number of reticulation nodes inferred in each case (Figure S2). The number of predicted hybridization events increases when the threshold value decreases and grows quickly with a decreasing threshold when species divergence times are small (scenarios 1-4 and 8-11). In these cases with small thresholds, ILS generates incongruent gene trees that support different clusters. The point when the number of hybridizations starts to grow corresponds approximately to a 20% threshold, even for scenarios where no gene flow is present (α = 0; scenarios 1, 8, and 15). Therefore, to evaluate performance of the consensus network method, we chose a 20% threshold. Consensus networks were reconstructed using the command-line interface of Dendroscope, choosing the cluster-network consensus option.³⁴ A schematic representation of the process applied to recover consensus species networks appears in Figure S3a.

Parsimony

We used the method of Yu et al,¹⁷ limiting the number of inferred hybridization events. To identify a promising strategy to limit the estimated number of hybridizations in the species network, we analyzed the behavior of 2 quantities that can potentially be used to inform network inference: number of extra lineages (NEL) and estimated ancestral species contribution toward hybridization $(\widehat{\alpha })$. Number of extra lineages is calculated as a sum over all the species tree branches, summing the number of gene tree lineages existing within each species tree branch minus 1, given the estimated species history. We examined how NEL and $(\widehat{\alpha })$ change as the number of allowed hybridizations grows, considering multiple scenarios with different values for the species divergence time and true value of α (scenarios 1-4, 8-11, and 15-18). We performed this evaluation on our largest locus sets, with 250 gene trees (Figure S4).

Because each additional hybridization provides alternative routes for gene trees to travel through the species tree, NEL decreases when the method is permitted to include a larger number of inferred hybridizations (Figure S4). It might be expected that NEL would decrease rapidly until the true number of hybridizations in the species network is reached and only more slowly afterward with additional “false-positive” hybridizations; however, in most cases, the decrease in NEL with increasingly many permitted hybridizations was linear, suggesting that no particular pattern is evident in NEL when the true number of hybridizations is reached. We therefore proceeded only using $(\widehat{\alpha })$.

In their empirical application, Yu et al¹⁷ added hybridizations to the inferred species network until extra hybridizations become skewed, with a small contribution from one of the parental lineages. To evaluate the possibility of using such a strategy systematically, we examined the distribution of inferred $(\widehat{\alpha })$ values when 1, 2, or 3 hybridizations were allowed in the inferred network (Figure S5).

We observed that when species divergence times are high, the hybridization in a 1-hybridization network generally has a value of $(\widehat{\alpha })$ near the true α (scenarios 16-18). As additional hybridizations were permitted, the $(\widehat{\alpha })$ values became more skewed toward 1 parent. This pattern suggested that the Yu et al¹⁷ strategy was sensible for these cases. We therefore adopted an approach that permits increasingly many hybridizations in the inferred network until a network is reached in which at least 1 hybridization is >90% skewed toward 1 parent.

Thus, in summary, our strategy for MP network inference used a sequential process, allowing up to 3 hybridizations (Figure S3b). A network allowing 1 hybridization event was inferred. If the predicted species history had 1 species contributing at a level lower than 10%, then a network with 0 hybridization events (MDC species tree) was recorded as the final inferred species history. Otherwise, a network allowing 2 events was considered; the 2-hybridization network does not necessarily contain the original 1-hybridization network. For the 2-hybridization network, only if in both hybridization events distinct parental lineages contributed at a level of 10% or higher, inference was continued. Otherwise, the 1-hybridization network was recorded as final. For the 3-hybridization network, if all 3 hybridizations were less than 90% skewed, then the network was recorded as final. Otherwise, the 2-hybridization network was recorded.

ML using PhyloNet

The ML network was inferred using methods of Yu et al,²¹ as shown in Figure S6a. Inference was performed in PhyloNet_3.5.4. We tested networks with increasingly many hybridizations (up to 3) using the AIC³⁵:

$$\mathrm{AIC}=-2\log L-2k$$ (2)

where L is the likelihood of the species relationship graph, its branch lengths, and values of α given a collection of gene trees, as generated by PhyloNet, and k is the number of estimated parameters, identified as the number of branches of the species network whose branch lengths are estimated plus 1 for each estimate of α. The number of parameters increases by 4 with each additional hybridization: 3 additional branch lengths and 1 extra α value. If AIC for a network with a larger number of hybridizations exceeded the AIC of a simpler species history, then we stopped the inference and recorded the simpler network as the final one.

ML using STEM-hy

The STEM-hy program is designed for testing a specified hypothesis about hybrid origin of a species rather than for estimating a hybridization history.^24,25 To apply STEM-hy (Figure S6b), for each set of simulated gene trees, we first used STEM to infer the species tree using gene trees. We also generated a list of up to 3 most-supported candidate hybridizations. To identify candidates, we used the consensus network approach with the threshold set to values ranging from 8% to 24%, with a step of 2%. Starting with 8%, if the inferred consensus network contained 3 or fewer hybridizations, these were chosen as the candidates. If the inferred consensus network contained more than 3 hybridizations, then the threshold was sequentially increased until the inferred network had 3 or fewer hybridizations. This condition was always achieved at a threshold no larger than 24%.

If a candidate hybridization was consistent with the species tree (in the sense that a cluster containing the descendants of the hybridization and the remaining descendants of one of its parental taxa was displayed by the species tree), then we tested them using STEM-hy. Otherwise, it was discarded.

To test candidate hybridizations with STEM-hy, we made some adjustments to the gene trees. STEM-hy allows only 1 hybrid species at a time and permits hybridization only between sister lineages. Therefore, in each gene tree, we retained 1 outgroup species, 1 species representing the hybrid lineage, and 1 lineage for each parent; tips representing other species in the gene trees were dropped. A species tree was estimated with STEM for the modified gene trees. If the inferred species tree on the modified gene tree set was displayed by the species tree on the full taxon set, then AIC for the species network including the candidate hybridization was compared with AIC for the species tree on the modified gene tree set to evaluate a candidate hybridization for inclusion in the final species network; otherwise, the hybridization was rejected. The hybridization was incorporated if its associated AIC was smaller than AIC for the species tree without the hybridization, and the inferred hybridization was less than 95% skewed.

Each potential hybridization was tested with STEM-hy independently from the others, and all supported hybridizations were incorporated into the estimated species network.

Evaluating inferred species histories

To evaluate the performance of species network reconstruction methods, we compared the topology of the inferred network with the topology of the true network or tree (in the α = 0 case) used in simulations. We used the cluster-based distance measure of topological differences between 2 networks^32,36 implemented in PhyloNet:

$$m\left(N_1,N_2\right)=\frac{\left(\frac{\left|C_1\backslash C_2\right|}{\left|C_1\right|}+\frac{\left|C_2\backslash C_1\right|}{\left|C_2\right|}\right)}{2}$$ (3)

where C₁ and C₂ are the sets of clusters induced by networks N₁ and N₂, respectively. For a pair of trees, this measure becomes the normalized Robinson-Foulds distance. For each evolutionary scenario, data set size, and species tree or network inference method, we assessed the performance as the average distance between the inferred and the true species network or tree across 10 replicates. Standard errors were computed as standard deviations of the distance between the inferred and true species network or tree across 10 replicates, divided by $(\widehat{\alpha })$.

We also explored the number of hybridization events included in the final network by different methods on the sets of 250 loci in 10 repeated experiments.

Results

Species divergence time

Topological difference between gene trees is one source of information for uncovering the presence of horizontal processes in species evolution. Other mechanisms, however, for instance, ILS, might also generate gene tree discordance. The amount of ILS is determined by the branch lengths separating species divergences, as measured in coalescent units. We study how divergence time parameters, and consequently the amount of ILS, influence network inference.

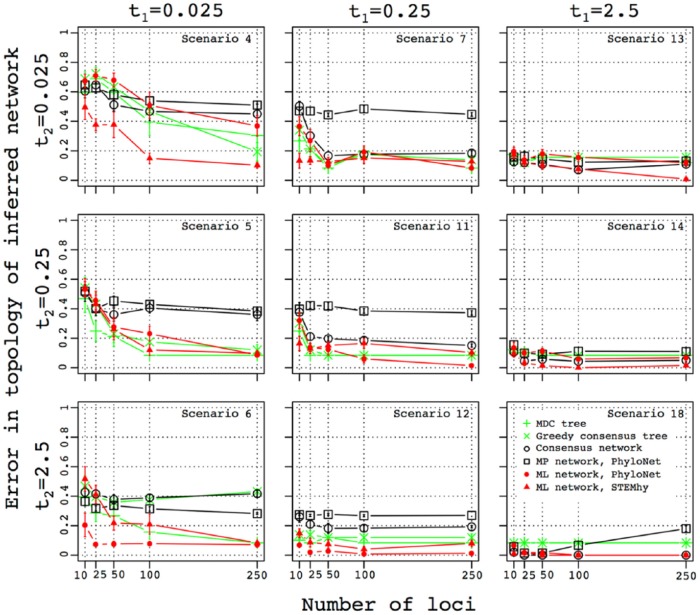
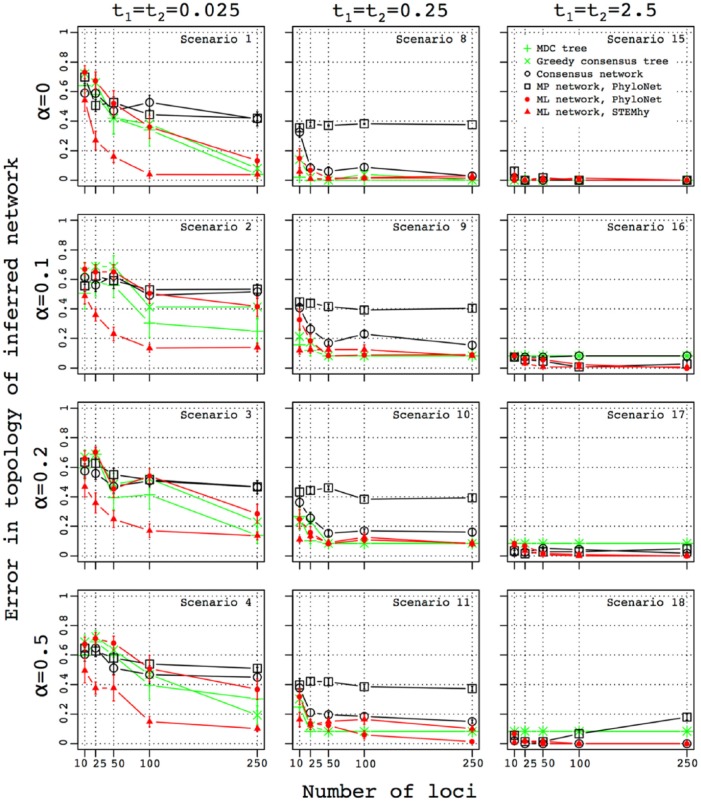
Figure 3 displays the error in species network topology estimation when gene trees are simulated on a species network whose internal branch lengths t₁ and t₂ take values of 0.025, 0.25, and 2.5. Each of the 9 combinations of values for t₁ and t₂ appears in a different panel. The parental contributions associated with the hybridization, α, are held constant at .5. The error is plotted for each of the various methods as a function of the number of loci used.

Figure 3.

Influence of species divergence time and number of loci on the accuracy of the inferred topology of the species network. The error in the topology of the inferred network was measured as the mean cluster distance between true and inferred networks (equation (3)). For each choice of the number of loci used for species network or tree inference, standard error was computed using 10 replicate simulations. The number of loci used for species network inference is plotted along the x-axis.

For instance, the central panel provides results for scenario 11. As shown on the top and left of the figure, t₁ = t₂ = 0.25. The x-axis shows the number of loci used for the inference, from 10 to 250. The y-axis illustrates error in species network topology estimates for different methods, measured as the cluster distance between the true and the inferred networks, considering for completeness 2 tree inference methods alongside the 4 network inference methods that form the focus of our analysis. Trends for the various approaches appear with different colors and symbols, as described in the inset in the bottom right panel. The position of the symbol gives the mean error in species network topology estimation for the method, and the bars represent standard error of the mean across 10 replicate simulations. For all methods, this panel shows a decreasing error rate with an increasing number of loci. At 250 loci, the error rate is lowest for ML-PhyloNet.

In all 9 panels, for most methods, the accuracy of species network inference improves when considering larger numbers of loci. Accuracy also improves when t₁ and t₂ increase from 0.025 to 0.25 and 2.5 coalescent units. For t₁ = 0.025, the performance generally improves with an increase in t₂ from 0.025 to 0.25. When 250 gene trees are used and t₂ = 0.25, the error in species network topology estimation drops from the range 0.1-0.5 (50%-90% of clusters are present in both true and inferred networks) to 0.1-0.4 (60%-90% of clusters are present in both true and inferred networks). When t₂ is increased further to 2.5 coalescent units, the accuracy does not improve substantially and does not achieve a level of no error for any of the methods.

Setting t₁ to 0.25 leads to a similar trend. When 250 gene trees are used, as t₂ increases from 0.025 to 0.25, the error in species network topology estimation drops from 0.1-0.2 to 0-0.2 for all methods except MP-PhyloNet. MP-PhyloNet has the poorest performance when t₂ = 0.025, becoming comparable with the other methods only when t₂ reaches 2.5. At t₂ = 2.5, ML-PhyloNet achieves 0 error.

When t₁ = 2.5, the performance of the different methods is generally good, improving gradually with increasing t₂. When t₂ reaches 2.5, most methods recover the true species network even when the number of loci is small.

Similar behavior is observed when t₂ is set to a fixed value, 0.025, 0.25, or 2.5, and t₁ is varied. The accuracy of species network inference is consistently higher in this case than when the roles of t₁ and t₂ are reversed. For instance, when t₂ = 0.025 and t₁ = 2.5, the error for different methods lies between 0 and 0.2, and ML-STEM-hy recovers the correct species network when 250 loci are used. The error is lower than when t₂ = 2.5 and t₁ = 0.025.

Overall, the likelihood methods, ML-PhyloNet and ML-STEM-hy, tend to produce lower error than consensus and parsimony methods, and they have among the lowest error rates in rather challenging simulation conditions with t₁ and t₂ both set to 0.25 or less. MP-PhyloNet produces an unusual pattern in scenario 18 when t₁ and t₂ are both set to 2.5. In this case, the error increases with an increasing number of gene trees in the data set. A similar trend, but not as pronounced, is sometimes observed for the consensus network method (scenarios 6 and 13).

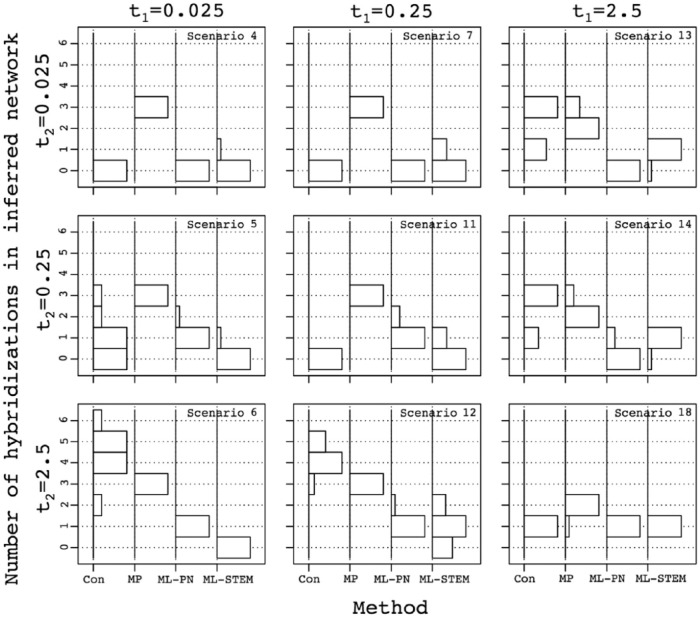
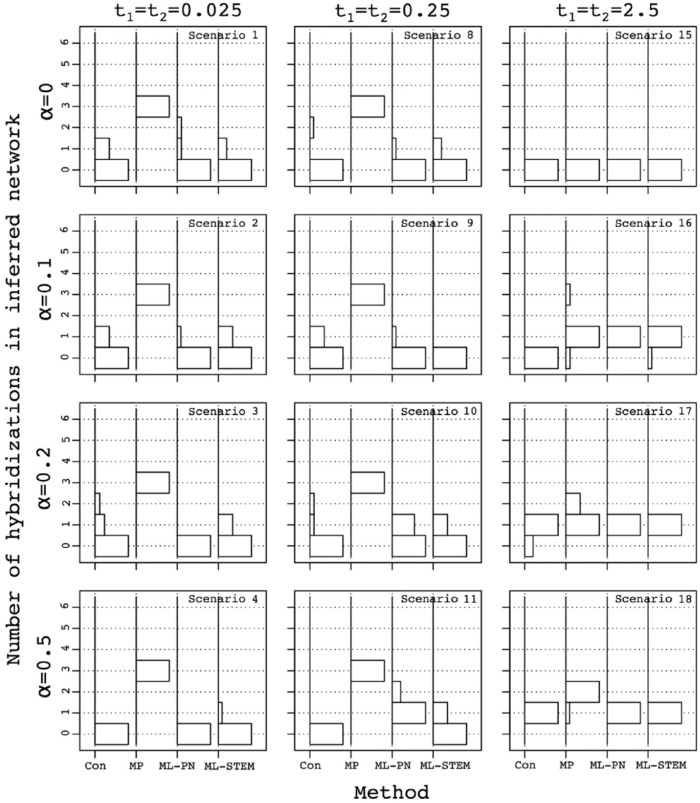
To understand whether some of the methods over- or underpredict the number of hybridization events, we examined the estimated number of hybridizations in the networks inferred using the largest number of gene genealogies considered as 250 (Figure 4). Recall that the true number of hybridizations in the simulation is 1. Results for the various scenarios are arranged, as shown in Figure 3, with t₁ and t₂ shown on the top and left sides of the figure. The numbers of hybridizations inferred by each of the species network reconstruction methods on 10 replicate data sets of 250 gene trees are summarized as histograms. For instance, the central panel considers scenario 11. In this case, consensus and ML-STEM-hy underpredict hybridizations, detecting no events for most replicates. MP-PhyloNet overpredicts hybridizations, inferring 3 events for all the replicates. ML-PhyloNet detects the correct value of 1 hybridization for most replicates.

Figure 4.

Influence of species divergence time on the inferred number of hybridization events in the inferred species networks. Histograms on the y-axes show the distribution of the number of hybridization events in the networks reconstructed using various species network inference methods, across 10 sets of 250 gene trees. Methods are shown on the x-axes: Con, consensus network; MP, MP network inferred using PhyloNet; ML-PN, ML network inferred using PhyloNet; ML-STEM, ML network inferred using STEM-hy. The maximum number of hybridizations was 6 and only occurred for consensus networks; in other cases, our implementation limited the maximum to 3. ML indicates maximum likelihood; MP, maximum parsimony; PN, PhyloNet.

For each scenario and each method, the species network inferred most frequently among replicates with the largest number of gene trees, 250, appears in Figure S7a. Recall that the true species network topology is shown in Figure 2. Inferred networks are arranged as shown in Figure 3, with t₁ and t₂ shown on the top and left sides of the figure. For instance, the central panel considers scenario 11. In this case, consensus recovers a species tree with a multifurcation in 8 of 10 replicates, and MP-PhyloNet recovers a network with a complex structure in 3 of 10 replicates. ML-STEM-hy recovers a species tree that corresponds to one of the ancestry paths in the species network in 5 of 10, and MP-PhyloNet captures the correct species network in 8 of 10.

When t₁ = t₂ = 2.5 (scenario 18), 3 of the methods predict 1 hybridization event in all 10 replicates. This result is not surprising as these methods also infer the correct species network (Figure 3). The poorer performing MP-PhyloNet, however, predicts 2 events for most replicates (Figures 4 and S7a).

When one of the internal branch lengths, t₁ or t₂, is set to 2.5 and the other is smaller (scenarios 6, 12, 13, and 14), the consensus network method overpredicts the number of hybridizations and generally recovers a complex network (Figure S7a). At the same time, it tends to underpredict the number of hybridizations when both internal branches are shorter than 2.5 (Figure 4, scenarios 4, 5, 7, and 11) and often returns unresolved species trees with multifurcations (Figure S7a).

Likelihood methods predict networks with 1 or 0 hybridization events in most cases. ML-PhyloNet underpredicts the number of hybridizations in 4 scenarios: when t₂ = 0.025, independently of the value of t₁ (Figure 4, scenarios 4, 7, and 13), and when t₂ = 0.25 and t₁ = 2.5 (Figure 4, scenario 14). The inferred network is generally a tree that corresponds to one of the ancestry paths in the true species network (Figure S7a). For the other 5 scenarios, when t₂ = 2.5, independently of t₁ (scenarios 6, 12, and 18), and when t₂ = 0.25 and t₁≠2.5 (scenarios 5 and 11), it predicts 1 hybridization for most replicates (Figure 4) and generally returns the correct species network topology (Figure S7a).

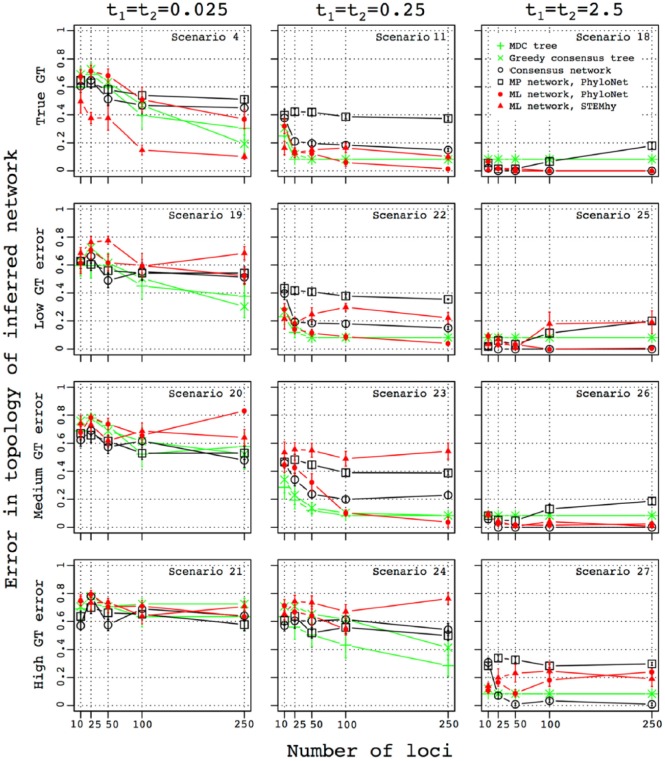
Figure 7.

Influence of the level of error in gene tree (GT) estimation and number of loci on the accuracy of the inferred topology of the species network. The error in the topology of the inferred network was measured as the mean cluster distance between true and inferred networks (equation (3)). For each choice of the number of loci used for species network or tree inference, standard error was computed using 10 replicate simulations. The number of loci used for species network inference is plotted along the x-axis.

ML-STEM-hy is more prone than ML-PhyloNet to underprediction of the number of hybridizations. It infers 0 hybridizations for most replicates (Figure 4) in 5 scenarios: when t₁ = 0.025, independently of t₂ (scenarios 4, 5, and 6), and when t₁ = 0.25 and t₂ < 2.5 (scenarios 7 and 11). Although the method does not identify the hybridization event, it does recover a species tree that corresponds to one of the ancestry paths in the species network (Figure S7a). For the other 4 scenarios, when t₁ = 2.5, independently of t₂ (scenarios 13, 14, and 18), and when t₁ = 0.25 and t₂ = 2.5 (scenario 12), it tends to predict 1 hybridization event (Figure 4) and generally captures the correct species network (Figure S7a).

This collection of analyses indicates that internal species network branch lengths have strong effects on the performance of the inference methods, with the branch length of the edges following the hybridization forward in time (t₁) having a stronger effect than the branch length immediately preceding the hybridization (t₂). If the branches are long, then likelihood and consensus generally recover the correct species history, even when a small number of gene trees are used. If the branches are shorter, then the more sophisticated likelihood methods are required for minimizing the error. However, if the branches are short, then none of the methods reliably recovers the correct species history even when examining 250 gene genealogies.

Parental species contributions

Next, we investigate the influence of the skew in parental species contributions on species network inference. As part of this analysis, we also evaluate how frequently hybridizations are identified when they are absent from the species history.

Similar to Figure 3, Figure 5 displays the error in species network topology estimation as a function of the number of sampled loci, except that here t₁ = t₂, with values of 0.025, 0.25, and 2.5, and the parental contribution associated with the hybridization, α, takes values of 0, .1, .2, and .5. Figure 6 represents similar information to that depicted in Figure 4. Figure S7b shows the most frequently recovered species network topologies, similar to Figure S7a.

Figure 5.

Influence of the species contributions toward the hybridization event (α) and number of loci on the accuracy of the inferred topology of the species network. The error in the topology of the inferred network was measured as the mean cluster distance between true and inferred networks (equation (3)). For each choice of the number of loci used for species network or tree inference, standard error was computed using 10 replicate simulations. The number of loci used for species network inference is plotted along the x-axis.

Figure 6.

Influence of the species contributions toward the hybridization event (α) on the inferred number of hybridization events in the inferred species networks. Histograms on the y-axes show the distribution of the number of hybridization events in the networks reconstructed using various species network inference methods, across 10 sets of 250 gene trees. Methods are shown on the x-axes: Con, consensus network; MP, MP network inferred using PhyloNet; ML-PN, ML network inferred using PhyloNet; ML-STEM, ML network inferred using STEM-hy. The maximum number of hybridizations was 6 and only occurred for consensus networks; in other cases, our implementation limited the maximum to 3. ML indicates maximum likelihood; MP, maximum parsimony; PN, PhyloNet.

With no hybridization, α = 0, all the methods except MP-PhyloNet and consensus achieve low error (0-0.2) on 250 gene trees (Figure 5, scenarios 1, 8, and 15). The low error rate occurs even when t₁ = t₂ = 0.025, at which a large amount of ILS occurs in the gene trees (scenario 1). When t₁ and t₂ increase to 0.25, all methods except MP-PhyloNet recover the correct species history with 250 gene trees (scenario 8); MP-PhyloNet instead predicts a large number of hybridizations (Figures 6 and S7b, scenarios 1 and 8). When t₁ and t₂ increase further to 2.5, the methods all recover the correct species history even when the number of loci is small (Figure 5, scenario 15).

In the case of highly skewed hybridization, α = .1, for t₁ = t₂ = 0.025, the error in species network estimation increases for all the methods in comparison with the α = 0 scenario (Figure 5, scenario 2). Most methods still find no hybridization (Figure 6), but ML-PhyloNet and ML-STEM-hy do identify species trees corresponding to ancestry paths in the species network (Figure S7b, scenarios 2 and 9). When t₁ and t₂ grow to 0.25, error decreases for all methods except MP-PhyloNet (Figure 5, scenario 9). However, correct species relationships are not recovered by any of the methods, even with data sets of 250 gene trees. This result is largely attributable to a failure to detect highly skewed hybridization as most methods identify 0 hybridizations (Figure 6). Finally, when t₁ and t₂ increase to 2.5, the correct species network is often obtained when 100 or more loci are sampled (Figure 5, scenario 16). The consensus method does not find this skewed hybridization (Figures 6 and S7b).

A similar trend is observed for the less skewed α = .2, except that in this case, all methods recover the correct species network when t₁ = t₂ = 2.5, even with a small number of sampled loci (Figure 5, scenario 17). The correct species network and number of hybridizations are identified as well (Figures 6 and S7b).

The relationship between error in species network estimation and the number of loci in the data set is also similar when hybridization becomes symmetric, α = .5 (Figure 5). One exception here is MP-PhyloNet, for which error increases with an increasing number of loci for scenario 18 (t₁ = t₂ = 2.5, α = .5).

Overall, ML-PhyloNet and ML-STEM-hy produce lower error than other methods, with ML-PhyloNet performing better in scenario 11 and producing the correct species network and ML-STEM-hy registering lower error for t₁ = t₂ = 0.025 (Figure 5, scenario 4). Consensus and MP-PhyloNet demonstrate similar, relatively inaccurate, performance when t₁ = t₂ = 0.025. Consensus improves, however, when t₁ and t₂ increase to 0.25, with error more similar to likelihood-based methods (Figure 5, scenarios 8-11), but failing to recover hybridization when it is present (Figure 6). It fails to identify highly skewed hybridization, even when internal species network branches are long (scenario 16), although it reports a species tree that represents an ancestry path encoded by the true species network (Figure S7b). Otherwise, it performs well in this time setting (scenarios 17 and 18).

Together, our results indicate that the parental species contribution, when hybridization is present, has a generally smaller effect on the performance of the inference methods than the branch lengths of the species network. Skewed hybridizations are as hard to detect as symmetric events when internal branches of the network are not long. If the branches are long, however, then most of the methods detect even highly skewed hybridizations.

Errors in gene trees

To address the possibility that errors in gene tree inference might influence the performance of species network inference methods, we infer species histories from erroneous gene trees, comparing the reconstructed history with the true assumed scenario.

As shown in Figure 3, Figure 7 displays the error in species network topology estimation as a function of the number of sampled loci. Here, internal branch lengths t₁ and t₂ are equal, taking values of 0.025, 0.25, and 2.5. The parental species contribution associated with the hybridization, α, is set to .5. Different error rates applied to the gene genealogies are shown in different rows. Figure 8 represents similar information to that depicted in Figure 4. Figure S7c shows the most frequently recovered species network topologies, similar to Figure S7a.

Figure 8.

Influence of the level of error in gene tree (GT) estimation on the inferred number of hybridization events in the inferred species networks. Histograms on the y-axes show the distribution of the number of hybridization events in the networks reconstructed using various species network inference methods, across 10 sets of 250 gene trees. Methods are shown on the x-axes: Con, consensus network; MP, MP network inferred using PhyloNet; ML-PN, ML network inferred using PhyloNet; ML-STEM, ML network inferred using STEM-hy. The maximum number of hybridizations was 6 and only occurred for consensus networks; in other cases, our implementation limited the maximum to 3. ML indicates maximum likelihood; MP, maximum parsimony; PN, PhyloNet.

When t₁ = t₂ = 0.025, all methods already suffer from a high error rate in the inferred topology, which increases even further with added errors in gene trees. The error is especially pronounced for ML-PhyloNet, for which the highest error level of ~0.8 is observed for scenario 20 when 250 gene trees are used (Figure 7). The high level of error in the species network topology is not associated with strong overprediction of hybridizations, as all the methods except MP-PhyloNet predict 0 to 2 hybridizations (Figure 8). The methods generally do not have a single most frequently inferred network topology (Figure S7c).

When t₁ = t₂ = 0.25, the error in the species network topology increases for ML-STEM-hy when a medium level of gene tree error is specified and for consensus at a high gene tree error level (Figure 7, scenarios 23 and 24). ML-PhyloNet never finished with 250 highly erroneous gene trees, but a high error rate in inferred species networks was obtained for 100 loci (Figure 7).

When t₁ = t₂ = 2.5, inference is more robust to gene tree errors, and accuracy generally remains the same for all the methods for low and medium gene tree error levels. If a high level of gene tree errors is used, however, then methods relying on likelihood exhibit more errors in the inferred network topology (Figure 7, scenario 27). The decrease in accuracy in this case is also associated with an elevated number of predicted hybridizations (Figure 8). At the same time, consensus remains robust and infers the correct species network when 250 gene trees are used (Figure S7c).

In summary, this analysis shows that although likelihood methods perform better on the true gene trees, they are often more sensitive to error in gene tree inference than the consensus approach, and in some cases, they might overpredict the number of hybridizations.

Discussion

The occurrence of hybridization in eukaryotic species has prompted development of tools to reconstruct reticulate species histories. Although a number of approaches have been developed for this task, little data have been generated to comparatively assess the properties of the methods. We have reported a systematic simulation–based comparative study of the performance of several methods for species network reconstruction.

Comparative performance of methods

We find that ML-PhyloNet performs generally well and is often robust to extensive ILS and errors in gene tree estimation when symmetric hybridization events are considered (Figure 3, scenarios 11 and 12; Figure 7, scenarios 22 and 23). Although it does not usually overpredict hybridizations, it fails to recover skewed hybridizations in the presence of non-negligible ILS (Figure 6, scenario 10). As an additional note, ML-PhyloNet also suffers from a long computing time, making this approach unsuitable for large data sets.

The next best method is ML-STEM-hy, which uses consensus-based identification of potential hybridization events and refines the list of those events by testing them in an ILS-aware framework. This method is also reasonably robust to ILS (Figure 3, scenarios 12 and 14). It is, however, sensitive to errors in gene trees. It can underpredict the number of hybridizations (Figure 8, scenario 23), and it also underidentifies skewed hybridization events in the presence of ILS (Figure 6, scenario 10). A sometimes sizable difference in the sensitivity of the 2 ML approaches to errors in gene tree estimation is likely attributable to the fact that STEM-hy uses gene tree branch lengths, which are affected by gene tree errors, in the likelihood calculation, whereas PhyloNet uses only the somewhat more robust gene tree topology.

Another method that performs reasonably well is the consensus method, which is often robust to errors in gene trees (Figure 7, scenario 27). However, it can be more sensitive to ILS than methods built upon the coalescent model when it is applied to detect symmetric (Figure 3, scenarios 11 and 12) or skewed hybridizations (Figure 5, scenarios 9 and 10). Consensus underpredicts symmetric hybridizations when ILS is sufficiently large, but branches of the species network have similar lengths (Figure 6, scenario 11). It also underpredicts highly skewed hybridizations even when ILS is low (Figure 6, scenario 16). However, the method overpredicts hybridizations under some circumstances, for instance, when the species network includes both short and long branches (Figure 4, scenarios 6, 12, 13, and 14).

The method with the highest error in species topology estimation was MP-PhyloNet. Recall that the strategy we implemented for MP-PhyloNet involves adding hybridization events to the network until they become highly skewed toward one of the parental lineages or until the number of hybridizations reaches a critical value of 3. This method recovered the correct species history only for scenarios 15 and 17 (Figure 5), which included only long species network branches and no hybridizations or skewed hybridizations. With the same time settings but symmetric hybridization, for this approach, we observed increasing error in the species network topology with a growing number of loci (Figure 3, scenario 18). This pattern of increasing error with more loci might indicate statistical inconsistency of the MP-PhyloNet strategy. Networks inferred with MP-PhyloNet often contain a large number of hybridizations.

Simulation conditions

We examined several simulation conditions. For the species divergence, we evaluated long (2.5 coalescent units), short (0.25), and very short (0.025) species network branch lengths. These species tree branch lengths are likely to reasonably represent a range of values that occur in empirical phylogenies. The great ape tree is estimated to have some longer branches several coalescent units in length,³⁷ whereas larger phylogenies with many species often contain various branch lengths that span the range we consider.³⁸

We found that when species network branch lengths are long (2.5 time units), almost all the methods performed well and often recovered the correct species history, even with a small number of loci and in the case of skewed hybridizations (Figure 5, scenarios 15-18). When internal species network branches became shorter (0.25), however, only ML-PhyloNet had minimal error with symmetric hybridization when applied to 250 loci (Figure 5, scenario 11). Although none of the methods detected a skewed hybridization in these time settings (Figures 5 and 6, scenarios 9 and 10), most were more successful when hybridization was absent (Figure 6, scenario 8). With the shortest species network branch lengths (0.025), almost none of the methods recovered the correct species history even when hybridization was absent (Figure 5, scenario 1), suggesting that this setting might be too difficult for all of the methods.

Skew in parental species contributions toward hybridization has a major effect on the performance of the consensus method, which fails to detect highly skewed hybridizations even when species network branches are long (Figure 6, scenario 16). This factor has a similar effect on ML-PhyloNet and ML-STEM-hy when network branches are short (Figure 6, scenarios 9 and 10).

Conclusions

We note that the study remains limited due to several factors. First, only 4 approaches for hybridization network reconstruction were evaluated, and a number of other methods and strategies exist^14,39–43 or can be envisioned. Indeed, multiple promising methods, including SnaQ⁴³ and new algorithms in PhyloNet,⁴⁴ have been reported since the time that our simulations began and hence were not included in our pipeline; it will be important to include such methods in future simulation studies. We do note that we included representative methods from multiple methodological categories: consensus, parsimony, and likelihood.

We designed our simulations with a focus on homoploid hybridization events that form new species, a perhaps less common type of hybridization in comparison with hybridization that produces polyploids^6,45 or introgression from one species into an existing species.⁵ It will be useful to perform a similar evaluation of the properties of hybridization detection methods in such scenarios.

Our computationally convenient strategy for generating erroneous gene trees from true trees differs from the commonly used approach of simulating alignments with the true gene trees and then inferring (potentially erroneous) gene trees from the alignments using gene tree inference methods.^22,46 Although such simulations are informative for gaining mechanistic understanding of gene tree error production, we note that they require multiple parameters to describe sequence evolution, and our approach, although less mechanistically interpretable, makes it possible to characterize the effect of gene tree error in relation to a single error parameter.

Another limitation is the small number of parameter values included in the simulations; we also considered only a single species network, with a fixed time for the hybridization event, with only a single hybridization, and with substantial contributions from each hybridizing species. We did not explore the impact of the species network shape, the choice of which species to hybridize, or the number of hybridization events in the true species network. We also did not consider introgressive scenarios with very limited contributions to the hybridization of one of the ancestral species as we focused on methods designed for large contributions from both parental species. However, even with this limited sampling of the parameter space, we covered a wide range of data sets with different properties, testing methods in conditions ranging from difficult to easy.

Finally, we examined a relatively small maximum number of loci and a relatively small number of species in our model species network. Although the size of data sets now often exceeds the 250 loci that we consider,^38,47 the sizes that we have examined continue to be relevant to many studies.^48,49 In the future, as methods continue to develop, it will be of interest to evaluate relative performance using data sets of larger size. An important concern for large data sets is computational scalability, which has been of great interest in the study of species network methods.^22,50 The computational cost, particularly for likelihood methods, can become prohibitive quickly if the number of taxa grows to ~25 or more.⁵⁰

In summary, based on our results, we recommend ML-PhyloNet for data sets that include small numbers of taxa and few enough loci for computation to be feasible. For larger data sets, due to computational overhead associated with ML-PhyloNet, we also recommend a hybrid approach in which candidate hybridizations are detected using consensus and then tested in an ILS-aware ML framework; such a strategy with ML-STEM-hy performed reasonably well, although it did have the weakness that it was sensitive to errors in gene trees.