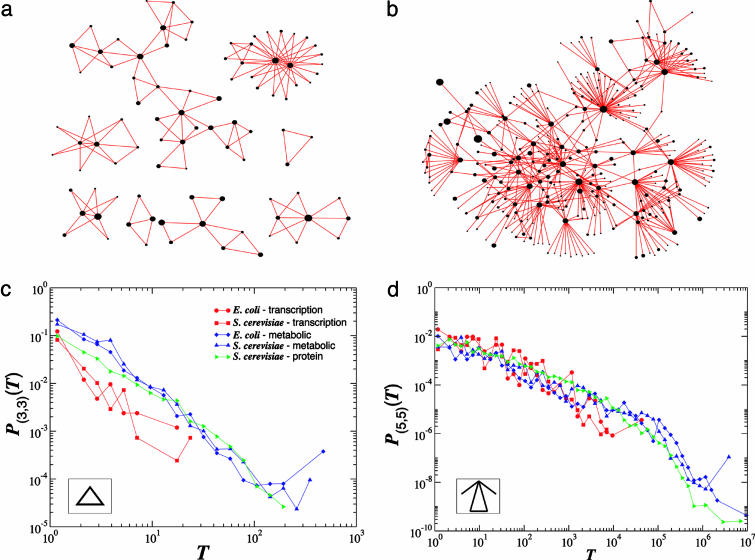
Fig. 2.

Subgraph distributions in cellular networks. a and b show all nodes in the S. cerevisiae transcription regulatory network that participate in triangle (3,3) and (5,5) subgraphs (depicted in Insets of c and d). The size (area) of each node is drawn proportional to its degree, k, in the full network, indicating that subgraphs tend to aggregate around the hubs. Indeed, although there are hubs that have only a few subgraphs around them, in most cases subgraph aggregation is seen only around highly connected nodes. Note that the (3,3) subgraphs of S. cerevisiae is above the percolation boundary (Fig. 1e), and therefore they are broken into small islands. In contrast, the (5,5) subgraph is well below the boundary, forming a fully connected giant component, with no isolated subgraphs, as predicted. c and d show the P(T) distribution of the number of (3,3) and (5,5) subgraphs, respectively, passing by a node, where T denotes the number of subgraphs of a selected kind passing by a given node. The plot indicates that for both subgraphs, P(T) approximates a power law P(T) ∼ T^–δ. Note the quite extended scaling regimes for some networks; e.g., for the (5,5) subgraph the scaling extends over four to five orders of magnitude. The δ exponents measured and predicted for each network are summarized in Table 2 and the supporting information.